Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SYNCHRONOUS MACHINES
5-29
Noting that
dfddfdad
adffdd
xxxxx
xxx
A
11
2
11
)(
11
++
=
−
=
2
11
2
2
)(
)()(
)(
ld
dddd
fd
ad
ld
dd
dfddfdad
ad
ad
xx
xxxx
x
x
xx
xx
xxxxx
x
xA
−
′
′′
−
′′
−
=
−
′
′′
−
′
=
++
=
(using (5.132) and (5.131))
Using the expression for x
1d
from (5.133), (5.134) can therefore be written as
q
ld
dddd
fdqdo
e
xx
xxxx
Ee
dt
d
T
′
−
′
′′
−
′′
−
+−=
′′
2
)(
)()(
1
d
ld
lddd
d
ld
dddd
i
xx
xxxx
xx
xxxx
−
′
−
′
′
′
−
−
−
′
′
′
−
′
′
−
+
)()(
)(
)()(
1
2
ψ
(5.135)
The second of the set of equations (5.126)
[]
ddfafddaffddffdfddfdd
ixxxxxxrA
dt
d
)()(
1
111111
o
−−−=
ψψψ
ω
(5.136)
doffd
ffd
df
dffd
d
d
Tx
x
x
xx
r
rA
′′
=
−
=
o
2
1
11
1
1
1
ω
Therefore, (5.136) can be written as
d
ffd
fdad
dfd
ffd
ad
ddo
i
x
xx
x
x
dt
d
T −−=
′′
11
ψψψ
dlddq
ixxe )(
1
−
′
−
−
′
=
ψ
(5.137)
The q axis equation is, from (5.126),
qq
q
qa
q
q
q
q
ir
x
x
x
r
dt
d
1
11
1
1
11
1
1
o
1
−−=
ψψ
ω
Multiplying both sides by
q
q
r
x
1
11
qaqqq
q
q
ix
dt
d
r
x
−−=
11
1o
11
ψψ
ω
With
q
q
aq
d
x
x
e
1
11
ψ
−=
′′
as defined in (5.127), and noting that
q
q
qo
r
x
T
1o
11
ω
=
′′
, the above can be written
as

SYNCHRONOUS MACHINES
5-30
dqqqdqo
eixxe
dt
d
T
′′
−
′′
−=
′′′′
)( (5.138)
q
e
′′
is given by, from (5.125),
dafddfdaffdfddadfafddq
xxxxAxxxxAe
1111111
)()(
ψ
ψ
−
+
−=
′′
which, using (5.128), (5.129) and (5.132), reduces to
d
ld
dd
q
ld
ld
q
xx
xx
e
xx
xx
e
1
ψ
−
′
′
′
−
′
+
′
−
′
−
′′
=
′′
(5.139)
The complete model is given by equations (5.135), (5.137), (5.138), and (5.127).
The electrical output power can be expressed as
qddqqdqqddqqdde
iixxriiieieieieP )()(
22
′′
−
′′
++−
′′
+
′′
=+=
(5.140)
Initial conditions
From initial power flow, terminal voltage and current (e and i) , and the power factor angle,
φ
,
will be known. From the phasor diagram of Figure 5.2,
φφ
φ
φ
δ
cossin
sincos
tan
1
o
irixe
irix
q
q
++
−
=
−
oooo
cos,sin
δ
δ
eeee
qd
=
=
)cos(,)sin(
oooo
φ
δ
φ
δ
−
=
−
= iiii
qd
(Note:
φ
is negative for lagging current)
ooo ddqqfd
ixireE
+
+
=
In the steady state the left hand sides of equations (5.135), (5.137) and (5.138) are zero.
Therefore, from (5.137)
ooo1
)(
dldqd
ixxe
−
′
−
′
=
ψ
(5.141)
Substituting
o1d
ψ
in (5.135) and simplifying,
oq
e
′
is obtained as
oo
)(
dddfdq
ixxEe
′
−
−
=
′
(5.142)
From (5.138)
oo
)(
qqqd
ixxe
′
′
−
=
′′
(5.143)
During the step-by-step computation
q
e
′
′
for equation (5.127) is obtained from equation (5.139).
An alternative representation of this model using voltages behind transient and subtransient
impedances as variables in the differential equations is as follows[9, 10]:
qdddfdqdo
eixxEe
dt
d
T
′
−
′
−−=
′′
)(
(5.144)
SYNCHRONOUS MACHINES
5-31
qdddqqdo
eixxee
dt
d
T
′′
−
′′
−
′
−
′
=
′′′′
)( (5.145)
dqqqdqo
eixxe
dt
d
T
′′
−
′′
−=
′′′′
)(
(5.146)
along with equation (5.127). The derivation is given at the end of this chapter.
Model 2 -- One equivalent damper winding on the
q axis only
With one equivalent damper winding on the q axis only,
=
=
0
,
1
fd
r
q
fd
r
e
VΨ
ψ
ψ
−
−
=
=
=
q
fd
r
aq
ad
sr
q
ffd
rr
r
r
x
x
x
x
111
,, RXX
All other submatrices are as in model 1.
Following the same steps as before,
−
=
−
ffd
ad
q
aq
rrsr
x
x
x
x
11
1
XXW
[]
+−
−
=−
−
ffd
ad
d
q
aq
q
rsrrsrss
x
x
x
x
x
x
2
11
2
1
XXXXW
−
−
=
−
q
q
ffd
fd
rrr
x
r
x
r
11
1
1
XR
and
=
−
q
q
aq
fd
ffd
ad
rsrrr
r
x
x
r
x
x
1
11
1
XXR
Therefore, from equations (5.123) and (5.124)
SYNCHRONOUS MACHINES
5-32
−
−−
−
−
=
q
d
ffd
ad
d
q
aq
q
fd
ffd
ad
q
q
aq
q
d
i
i
r
x
x
x
x
x
xr
x
x
x
x
e
e
)(
)(
2
11
2
1
11
ψ
ψ
(5.147)
and
−
−
=
qq
q
aq
dfd
ffd
ad
q
q
q
fd
ffd
fd
fd
q
fd
ir
x
x
ir
x
x
x
r
x
r
e
dt
d
1
11
1
11
1
1
o
0
1
ψ
ψ
ψ
ψ
ω
(5.148)
Defining the following quantities
,,
1
11
fd
fffd
ad
qq
q
aq
d
x
x
e
x
x
e
ψψ
=
′
−=
′
and using the expressions for transient reactances and time constants, equations (5.147) and
(5.148) can be expressed as
′
′
−
−
′
′
=
q
d
d
q
q
d
q
d
i
i
rx
xr
e
e
e
e
(5.149)
dqqqdqo
qdddfdqdo
eixxe
dt
d
T
eixxEe
dt
d
T
′
−
′
−=
′′
′
−
′
−−=
′′
)(
)(
(5.150)
Note that in the above equations, transient notations have been used for the q axis quantities so as
to be consistent with the notations for the d axis.
Model 3 -- no damper winding
Following the same procedure as before, the model can be derived as
′
−
−
′
=
q
d
d
q
qq
d
i
i
rx
xr
ee
e 0
(5.151)
qdddfdqdo
eixxEe
dt
d
T
′
−
′
−−=
′′
)( (5.152)
Saturation
An exact analysis of the effect of saturation in a synchronous machine is complex. The
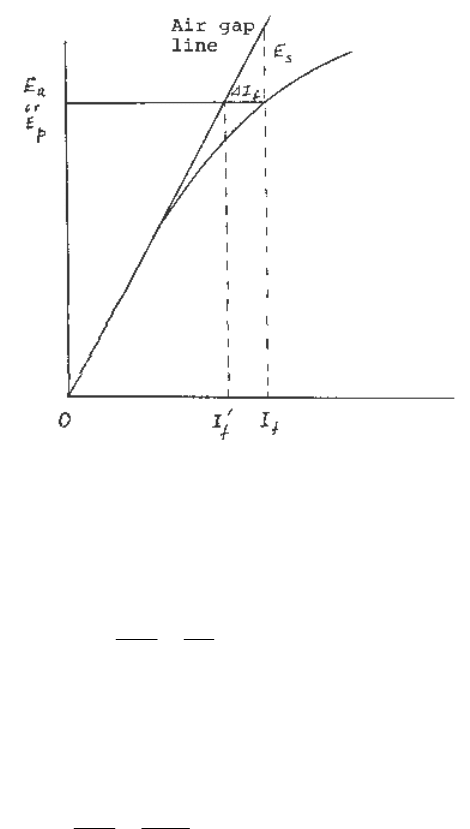
assumption is usually made that saturation is a function of the air-gap flux. A typical no-load
saturation curve is shown in Figure 5.3. The extension of the straight line portion of the curve is
known as the air-gap line.
SYNCHRONOUS MACHINES
5-33
Fig. 5.3 A typical no-load saturation curve of a synchronous machine.
It can be seen that the presence of saturation requires an additional field current (or mmf),
fff
III
′
−=∆ , over that required to generate the voltage E
a
on the air-gap line. A no-load
saturation factor may be defined as
a
s
f
f
E
E
I
I
S =
′
∆
=
(5.153)
Denoting the saturated value of x
ad
by x
adS
, we can write
fadfadS
IxIx
′
=
or
Sx
x
ad
adS
+
=
1
1
(5.154)
Saturation in cylindrical rotor machines
The assumption is made that
aqadqd
xxxx
=
= , , and that at a given field excitation, saturation is
a function of the total air-gap flux. Therefore, in the steady state, analogous to the no-load
saturation relationships (5.153), it can be stated that the phasor difference between the voltage
generated by the actual field current and the armature reaction drop (x
d
– x
l
)I is (1+S) times the
voltage behind the leakage reactance drop. The steady state phasor relationship including the
effect of saturation is shown in Figure 5.4.
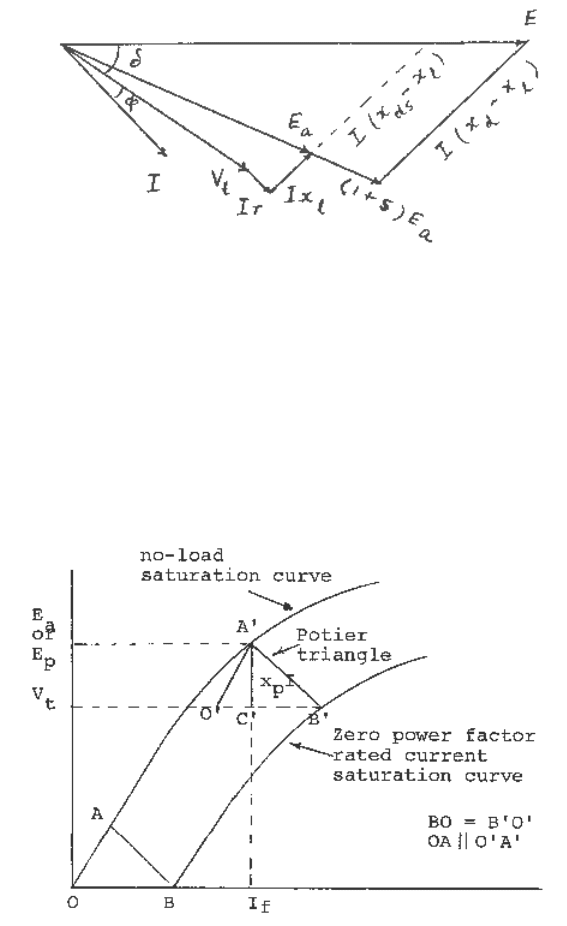
SYNCHRONOUS MACHINES
5-34
Fig. 5.4 Steady state phasor diagram of a cylindrical rotor
synchronous generator including saturation.
S is a function of the total air-gap flux (E
a
), and the field excitation (E). At constant field current,
S is a function of only the total air-gap flux. Evaluation of S under various loading conditions,
therefore, requires the complete load saturation characteristics which are usually not available.
The use of Potier reactance (or the transient reactance), which is generally greater than the
calculated leakage reactance, provides an empirical correction of the saturation factor obtained
from the no-load saturation curve to allow for load saturation. Potier reactance can be determined
from test as illustrated in Figure 5.5.
Fig. 5.5 Saturation characteristics for determination of Potier reactance.
Saturation in salient pole machines
In the case of salient pole machines, although the stator core and teeth are saturated to the same
extent in both the direct and quadrature axes, there is generally very little saturation in the
quadrature axis magnetic path in the rotor. Most of the saturation in the rotor exists in the body
of the pole, which is in the path of the direct axis flux. Therefore, the assumption is made that the
mmf required to overcome saturation can be divided into two components: one which is
dependent only on the total flux, the other dependent only on the direct axis flux. Denoting the
two saturation factors by S
1
and S
2
, the phasor diagram shown in Figure 5.6 can be constructed.
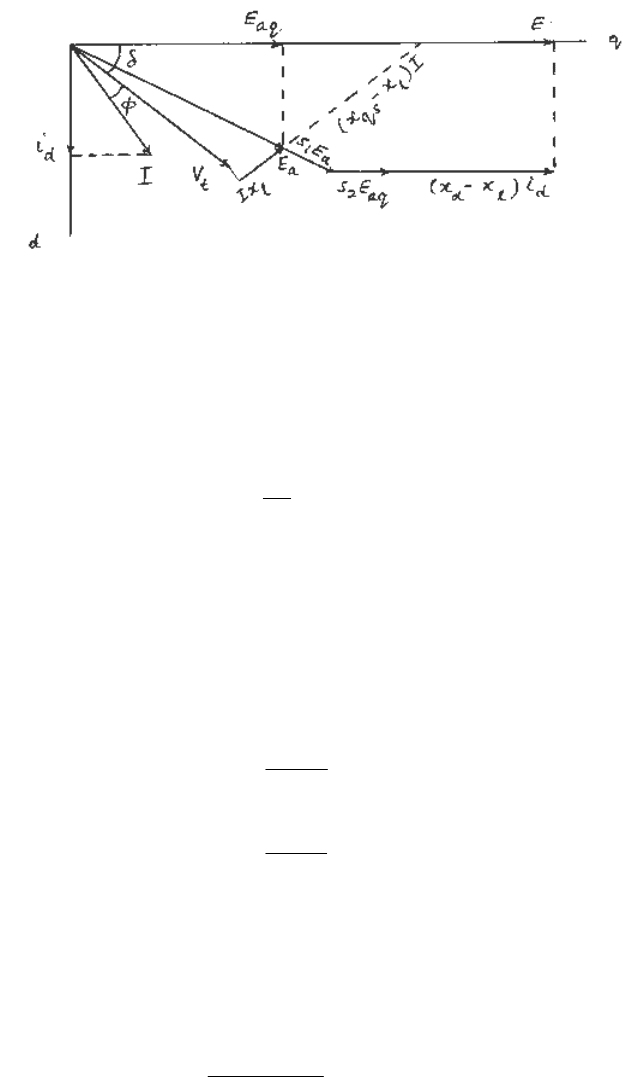
SYNCHRONOUS MACHINES
5-35
Fig. 5.6 Steady state phasor diagram of a salient pole
synchronous generator including saturation.
In practice, for both salient pole and cylindrical rotor machines, a single saturation factor, S
D
, can
be used to account for saturation on the direct axis. This may be obtained from the no-load
saturation curve using the Potier (or transient) reactance (5.153). The saturation factor, S
Q
, for
the quadrature axis may be taken as
D
d
q
Q
S
x
x
S = (5.155)
Inclusion of the effect of saturation in machine modeling
From the previous discussion it is apparent that saturation predominantly affects the mutual
reactances, x
ad
, x
aq
, although some of the rotor leakage reactances also saturate to some extent.
Therefore, in detailed machine modeling, where the equations are expressed explicitly in terms
of the mutual and leakage reactances, saturation can be accounted for by simply adjusting the
values of x
ad
and x
aq
during the step-by-step computation, according to
D
ad
adS
S
x
x
+
=
1
(5.156)
Q
aq
aqS
S
x
x
+
=
1
(5.157)
S
D
and S
Q
can be computed as described earlier. In a stability program it is more convenient to
use an analytic function defining the saturation factor at various points on the saturation curve.
One possible function is
AE
E
AEB
S
AE
p
p
p
D
p
>
−
=
≤
=
for ,
)(
for,0S
2
D
(5.158)
where A and B are constants which can be calculated by solving the equations
2.1/)2.1(
0.1/)0.1(
2
2.1
2
0.1
ABS
ABS
D
D
−=
−=
(5.159)

SYNCHRONOUS MACHINES
5-36
S
D 1.0
and S
D 1.2
are the values of S
D
at two points, E
p
= 1.0 and E
p
= 1.2, on the no-load saturation
curve (see Figure 5.3).
Changing the values of x
ad
and x
aq
continuously during the stability computation can be
cumbersome and time consuming. In less detailed machine models, it is desirable to use fixed
reactance values in the machine equations, and account for saturation using separate terms. This
can be accomplished as shown below.
Consider the model with one rotor circuit on each axis (field winding on the direct axis and one
amortisseur winding on the quadrature axis), as discussed under model 2. Rewriting the starting
point equations, using saturated values for the mutual reactances,
dadSfdfSadSfd
ixixx
−
+
= )(
ψ
(5.160)
fdadSdladSd
ixixx
+
+
−= )(
ψ
(5.161)
qaqSqqaqSq
ixixx
−
+
=
111
)(
ψ
(5.162)
qaqSqlaqSq
ixixx
1
)(
+
+
−=
ψ
(5.163)
fdfdfdfd
ir
dt
d
e +=
ψ
ω
o
1
(5.164)
dqd
ire
−
−=
ψ
(5.165)
qdq
ire
−
=
ψ
(5.166)
From (5.160)
fdfSdfdadSdfdad
fdfSdfdadSfd
ixiixSiix
ixiix
+−−−=
+
−
=
)()(
)(
ψ
(using (5.154))
pq
ad
f
dadfdffd
fdfSpqdfdad
E
x
x
Sixix
ixESiix
)1(
)(
+−−≈
+
−
−
≈
(assuming that the ratio of the saturation of the field leakage reactance to the saturation of the
mutual reactance is in proportion to the ratio of the field leakage reactance to the mutual
reactance)
pqdddfdadpqd
ffd
ad
fdadfd
ffd
ad
q
ESixxixESi
x
x
ix
x
x
e −
′
−−=−−==
′
∴
)(
2
ψ
(5.167)
or
qdddfdadq
eSixxixe
′
−
′
−
−=
′
)( (5.168)
From (5.161) and (5.166)
SYNCHRONOUS MACHINES
5-37
qpqddfdad
qdldfdadSdfdad
qdldfdadSq
irESixix
irixiixSiix
irixiixe
−−−=
−−−−−=
−
−
−=
)()(
)(
(5.169)
From (5.167) and (5.169)
qddqq
irixee
−
′
−
′
=
(5.170)
From (5.164)
fdfd
ffd
ad
fd
ffd
ad
fd
ffd
ad
ir
x
x
e
x
x
x
x
dt
d
−=)(
1
o
ψ
ω
or
fdadfdfdad
fd
fd
adq
fd
ffd
ixEix
r
e
xe
dt
d
r
x
−=−=
′
o
ω
(5.171)
From (5.168) and (5.171), we can write
qdddfdqdo
eSixxEe
dt
d
T
′
+−
′
−−=
′′
)1()( (5.172)
This equation is of the same form as derived previously neglecting saturation, except for the
additional term
q
eS
′
−
on the right-hand side, which accounts for saturation.
The equations for the d axis can be derived similarly. The complete model including saturation
effect is therefore as follows:
′
′
−
−
′
′
=
q
d
d
q
q
d
q
d
i
i
rx
xr
e
e
e
e
(5.173)
qdddfdqdo
eSixxEe
dt
d
T
′
+−
′
−−=
′′
)1()(
(5.174)
dqqqdqo
eSixxe
dt
d
T
′
+−
′
−=
′′
)1()( (5.175)
Network Model in
DQ Reference Frame
Consider a line between two buses, numbered 1 and 2, in a network. The voltage and current
relationship is
abcabcabcadc
dt
d
lr
,21212,1
viiv ++= (5.176)
where r
12
and l
12
are the resistance and inductance of the line.
Resolving the phase quantities along a set of synchronously rotating network D-Q axes using the
transformations (5.15) and (5.17),
O,2O
1
12O12O,1
)(
DQDQDQDQ
dt
d
lr eiTTie ++=
−
SYNCHRONOUS MACHINES
5-38
After carrying out the indicated matrix operation
O,2O12O12O12O,1 DQDQDQDQDQ
dt
d
llr eiiSie +++=
ω
(5.177)
where
−
=
000
001
010
S
In the steady state
ODQ
dt
d
i is zero. Even in the transient state this term is small compared to the
ω
ODQ
i term, and in conventional stability studies it can be neglected. The
ODQ
dt
d
i
term accounts
for the short-lived electrical transients that are present immediately after a disturbance.
Therefore, for balanced operation (e
O
= i
O
= 0), we can write (5.177) as
QDQQ
DQDD
eilire
eilire
212121
212121
++=
+
−
=
ω
ω
which, in per unit, become
QDQQ
DQDD
eixire
eixire
212121
212121
++=
+
−
=
(5.178)
Defining complex voltage and current
QDQD
jiiijeee +=+=
ˆ
,
ˆ
(5.178) can be expressed as
212121
ˆ
ˆ
)(
ˆ
eijxre ++=
or
)
ˆˆ
(
ˆˆ
ˆ
2112
12
21
eey
z
ee
i −=
−
= (5.179)
Thus the relationship between current and voltage in DQ reference is the same as that when
represented by conventional phasors. Therefore, for balanced operation, network equations using
the network impedance or admittance matrix as discussed in Chapter 1 will remain the same in
the DQ reference.
Transformation from machine to network reference frame
In the representation of synchronous machines the machine quantities are expressed in terms of
direct and quadrature axes that are oriented differently for different machines. For a multi-
machine stability analysis, it is therefore necessary to transform the machine currents and
voltages from the individual d-q axes (machine reference frame) to a common set of network D-
Q axes (network reference frame), before the network solution can be undertaken. Following the
network solution the quantities can then be transformed back to the machine reference frame for
use in the solution of the machine equations.
