Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

SYNCHRONOUS MACHINES
5-39
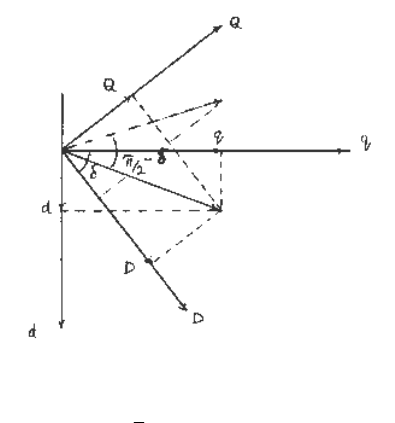
The principle of transformation is illustrated in Figure 5.7.
δ
is the angle between a machine q
axis and the network D axis. In order to transform from one set of axes to another, we rotate the
d-q axes along with the particular phasor (voltage or current) by an angle of π/2 -
δ
, so as to
make the two sets of axes coincide. In terms of the network reference frame the rotation can
therefore be expressed as
Fig. 5.7 Illustration of transformation of axes.
jqdjQD
j
+=+
− )
2
(
)(
δ
π
ε
(5.180)
or
jqdjjQD
+
=
+
+ )cos(sin)(
δ
δ
(5.181)
Separating the real and imaginary parts, the transformation can be expressed in matrix form as
−
=
Q
D
q
d
δδ
δδ
sincos
cossin
(5.182)
The reverse transformation can be expressed as
−
=
q
d
Q
D
δδ
δδ
sincos
cossin
(5.183)
Stability Computation in Multi-Machine Systems
For the purpose of this illustration and to keep the analysis simple, we will assume that the
network has been reduced retaining only the nodes at which machines are connected. As has
been pointed out in Chapters 3 and 4, working with the full network has computational
advantage as the network admittance matrix is generally very sparse. The modifications in the
computational steps that are required when working with the full network will be similar to those
using the classical machine model as discussed in Chapters 3 and 4.
For n machines, the current and voltage relationships in machine and network reference frame
can be written as, from (5.182),
VTe
ITi
=
=
(5.184)
SYNCHRONOUS MACHINES
5-40
where i (v) and I (V) are the vectors of the currents (voltages) in machine and network reference
frame, respectively.
=
=
=
=
MMMM
2
2
1
1
2
2
1
1
2
2
1
1
2
2
1
1
,,,
Q
D
Q
D
q
d
q
d
Q
D
Q
D
q
d
q
d
e
e
e
e
e
e
e
e
i
i
i
i
i
i
i
i
VeIi
and
−
−
=
O
22
22
11
11
sincos
cossin
sincos
cossin
δδ
δδ
δδ
δδ
T
Using machine model 1, for the purpose of illustration, the relationships between machine
internal and terminal voltages can be written, from equation (5.127), for n machines, as
eiZE
+
=
M
(5.185)
where
′′
′′
−
′′
′
′
−
=
′′
′′
′′
′′
=
OM
22
22
11
11
2
2
1
1
,
rx
xr
rx
xr
e
e
e
e
d
q
d
q
M
q
d
q
d
ZE
The network equations, after separating the real and imaginary parts, can be written in real form
as
VYI
N
=
(5.186)
where
−
−−
=
MM
L
L
L
L
2121
2121
12121111
12121111
gb
bg
gbgb
bgbg
N
Y
From (5.185)
eZEZi
11 −−
−=
MM
VTZTEZTeZTEZTiTI
111111111 −−−−−−−−−
−=−==
∴
MMMM
(5.187)
From (5.186) and (5.187)
[]
EZTTZTYV
11
1
11 −−
−
−−
+=
MMN
SYNCHRONOUS MACHINES
5-41
[]
EZTTZTYTVTe
11
1
11 −−
−
−−
+==
∴
MMN
(5.188)
The machine terminal currents are obtained from (5.185)
[
]
eEZi −=
−1
M
(5.189)
Electrical power output is obtained from (5.140).
The computational steps shown in (5.188) and (5.189) are equivalent to those described in
Chapter 4 (see equations (4.27), (4.28)), where the machine internal voltage in series with the
internal impedance is first converted to a current source and machine terminal voltage is obtained
directly by multiplying the vector composed of these currents by the inverse of the modified
network admittance matrix. In (5.188), the operation EZ
1−
M
is equivalent to converting the
voltage source into current source in machine reference frame. This is then transformed to
network reference frame, followed by multiplication by the inverse of the modified network
admittance matrix to obtain the machine terminal voltage. Finally, this is transformed back to the
machine reference frame. The machine current is then obtained from (5.189).
Note that in using machine model 1, since
qd
xx
′
′
≈
′
′
, they can be assumed equal and then
111 −−−
=
MM
ZTZT . Thus
[
]
TZTY
11 −−
+
MN
has to be inverted only once for each network
configuration. Also, with
qd
xx
′′
=
′′
, it is possible to work with equations in complex form thereby
reducing the computational burden considerably. Equation (5.188) would then be written as
[
]
EZTZYTe
ˆ
ˆ
11
1
1 −−
−
−
+=
MMN
(5.190)
where Ee
ˆ
and
ˆ
are the vectors of complex machine terminal and internal voltages, respectively.
N
Y is the complex network admittance matrix.
M
Z is a diagonal matrix of the complex machine
internal impedances
dii
xjr
′′
+
, and T is given by
=
−
−
O
)
2
π
(
)
2
π
(
2
1
δ
δ
ε
ε
j
j
T
Equation (5.189) would then become
[
]
eEZi
ˆ
ˆ
ˆ
1
−=
−
M
(5.191)
Note that in this formulation the non-generator buses can be retained. As has been pointed out in
Chapter 7, non-dynamic (or static) loads should be represented by constant impedance. Dynamic
loads (motor and non-motor) can be adequately represented by one of the induction machine
models discussed in Chapter 7. For the buses with impedance loads, the injected currents would
be zero, the block diagonal elements of
Z
M
would be 2 × 2 null matrix, the impedance having
been included in the network admittance matrix, and the corresponding elements of the
T matrix
would be 2
× 2 unit matrix. The network solution can then proceed as discussed in Chapter 4,
taking advantage of the sparsity of
Y
N
. Induction motor and other dynamic loads can be handled
following the procedure discussed in Chapter 8.
SYNCHRONOUS MACHINES
5-42
An iterative method for handling saliency
In the previous illustration using machine model 1 it was pointed out that since
qd
xx
′′
≈
′′
for most
synchronous machines they can be assumed equal and network computation can be greatly
simplified. For machine models 2 and 3 this assumption is not valid. However, equation (5.190)
can still be used when saliency is present, using an iterative technique.
Consider machine model 2. Rewriting the machine voltage equations (5.149)
qqddd
ixiree
′
−
+
=
′
(5.192)
ddqqq
ixiree
′
+
+
=
′
(5.193)
For
dq
xx
′
<
′
a voltage on the d axis is defined as
qdddd
ixiree
′
−
+
=
1
(5.194)
which is related to
d
e
′
by
qdqdd
ixxee )(
1
′
−
′
+
′
=
(5.195)
Equations (5.193) and (5.194) can be arranged in matrix form as
′
′
−
+
=
′
q
d
d
d
q
d
q
d
i
i
rx
xr
e
e
e
e
1
(5.196)
In (5.196) saliency has been removed. The new defined voltage
1d
e is undetermined, and this is
computed in an iterative way. The complete process in a multi-machine system can be
summarized as follows:
The matrix
[]
1
1
−
−
+
MN
ZY is formed only once for a particular network condition. At each
integration step
qd
ee
′′
and are known.
1d
e is determined for each machine from (5.195) using the
latest value of
q
i
. This voltage and
q
e
′
are then used in the voltage vector in (5.188). New values
of
q
i and
1d
e are computed for each machine from (5.188) and (5.195), respectively. The voltage
vector in (5.188) is then updated. The process is repeated until convergence is obtained.
The convergence is reasonably fast except immediately following a major disturbance. It can be
made faster by using some acceleration technique.
It is found that convergence is not achieved if in (5.195)
q
x
′
is greater than
d
x
′
. When
q
x
′
>
d
x
′
(for example, using machine model 3 when
q
x
replaces
q
x
′
and
q
x
>
d
x
′
), a voltage on the q axis
needs to be defined as follows, in order to achieve convergence.
dqqqq
ixiree
+
+
=
1
(5.197)
and this is related to
q
e
′
by
ddqqq
ixxee )(
1
′
−
+
′
=
(5.198)
The matrix equation corresponding to (5.196) is now
SYNCHRONOUS MACHINES
5-43
−
+
=
q
d
q
q
q
d
q
i
i
rx
xr
e
e
e
1
0
(5.199)
A similar procedure as before can now be followed.
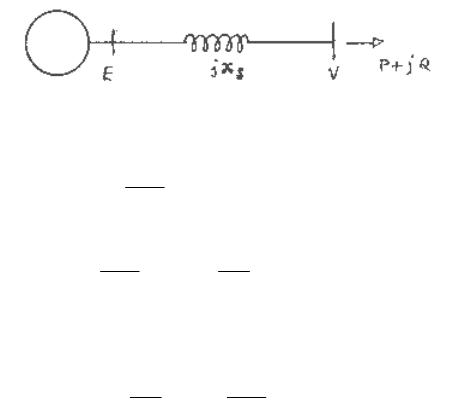
Generator Capability Curve
Consider a round rotor machine connected to an infinite system as shown in Figure 5.8. The
expressions for real and reactive powers supplied to the system, neglecting resistance, are given
by
Fig. 5.8 A round rotor machine connected to infinite bus.
δ
sin
s
x
VE
P
= (5.200)
ss
x
V
x
VE
Q
2
cos −=
δ
(5.201)
From (5.200) and (5.201) we obtain
22
2
2
=
++
ss
x
VE
x
V
QP
(5.202)
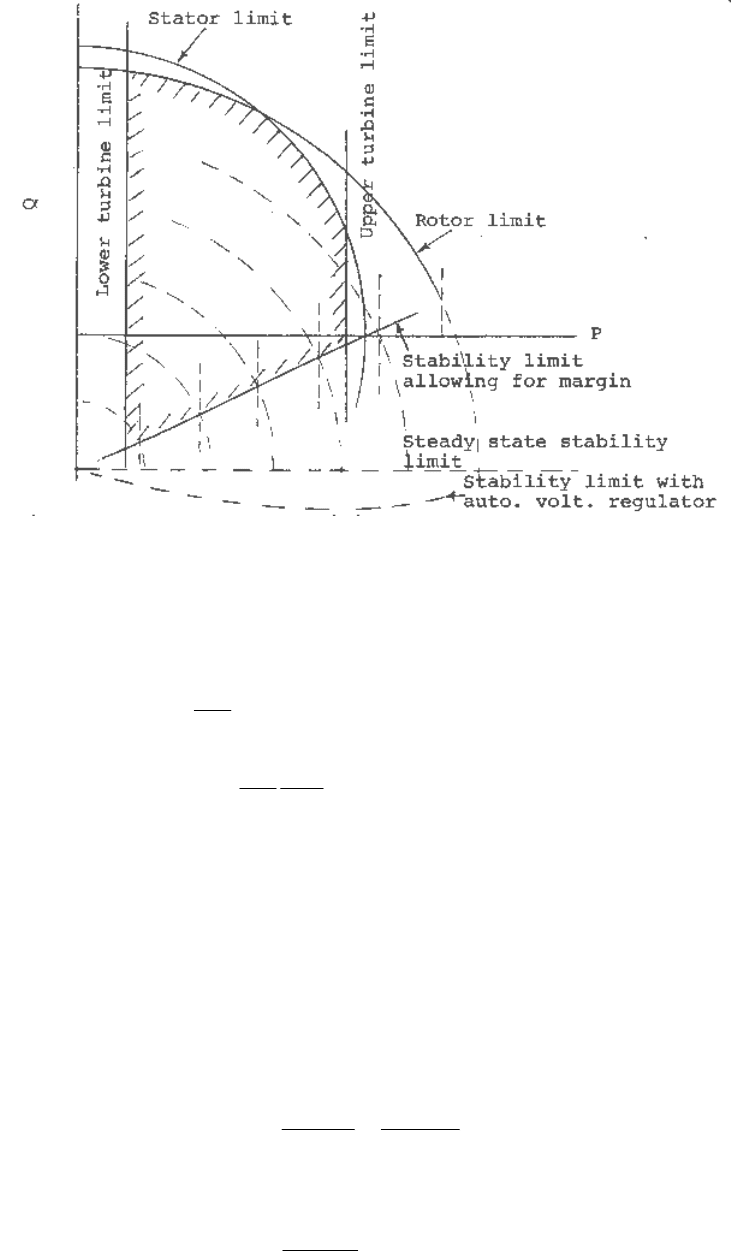
Equation (5.202) describes a circle with radius EV/x
s
and center located at (0, −V
2
/x
s
), using P
and Q as the axes of coordinates, as shown in Figure 5.9. For a given value of V we can draw a
series of circles corresponding to various values of the generator excitation voltage E.
The generator must be operated within the limits imposed by the stator and rotor heating, the
maximum and minimum allowable turbine outputs, and stability. The various limits are shown
on Figure 5.9. The stator limit is indicated by the circle of radius equal to the MVA rating with
center at the origin (0, 0). The rotor limit is indicated by the circle of radius E
max
V/x
s
with center
located at (0,
−V
2
/x
s
).
The theoretical steady state stability limit (
δ
= 90°) is indicated by the line parallel to the P axis
and at a distance
−V
2
/x
s
from it. This can be extended, as indicated in Figure 5.9, by the action of
automatic voltage regulator. It is customary to allow for a margin (10-15%) in the steady state
stability limit. The stability limit allowing for margin is obtained by first finding the power limit
for a given excitation. This is then reduced by the desired margin and the corresponding point on
the excitation curve is noted, as illustrated in the figure.
The complete operating region is shown by the shaded area. In practice some restriction may
apply due to transient stability or other considerations.
SYNCHRONOUS MACHINES
5-44
Fig. 5.9 Generator capability curve.
Stability Limit at Constant Field Voltage
Consider the single machine-infinite bus system shown in Figure 5.10. Using the synchronous
machine model 3 and neglecting armature and line resistances, we have
qdddfd
q
do
eixxE
dt
ed
T
′
−
′
−−=
′
′
)( (5.203)
em
PP
dt
dH
−=
2
2
o
2
δ
ω
(5.204)
qddqqqe
iixxieP )(
′
−
+
′
=
(5.205)
qqd
ixe =
(5.206)
ddqq
ixee
′
−
′
=
(5.207)
We also have
qebd
ixVe
−
=
δ
sin (5.208)
debq
ixVe
+
=
δ
cos
(5.209)
From (5.207) and (5.209), we have
ed
b
ed
q
d
xx
V
xx
e
i
+
′
−
+
′
′
=
δ
cos
(5.210)
Similarly, from (5.206) and (5.208), we have
eq
b
q
xx
V
i
+
=
δ
sin
(5.211)

SYNCHRONOUS MACHINES
5-45
Fig. 5.10 Phasor diagram of a synchronous machine connected to infinite bus through
a reactance.
Linearizing (5.203) - (5.205), (5.210) and (5.211), and noting that
∆E
fd
= 0, we have
qddd
q
do
eixx
dt
ed
T
′
∆−∆
′
−−=
′
∆
′
)( (5.212)
e
P
dt
dH
∆−=
∆
2
2
o
2
δ
ω
(5.213)
][)(
qdqddqqqqqe
iiiixxieieP
∆
+
∆
′
−
+
∆
′
+
′
∆=∆ (5.214)
δ
δ
∆
+
′
+
′
∆
+
′
=∆
ed
b
q
ed
d
xx
V
e
xx
i
sin
1
(5.215)
δ
δ
∆
+
=∆
eq
b
q
xx
V
i
cos
(5.216)
i
d
, i
q
, e
d
, e
q
, etc. are the values at the operating point and the prefix ∆ denotes the small changes
in the variables about the operating point.
Substituting (5.215) and (5.216) into (5.214), we have
]
sin
e
1
[i)-(
cos
])([
qqd
δ
δ
δ
δ
∆
+
′
+
′
∆
+
′
′
+
∆
+
′
−+
′
+
′
∆=∆
ed
b
ed
q
eq
b
ddqqqqe
xx
V
xx
xx
xx
V
ixxeieP
which can be written as
qe
ebaP
′
∆
+
∆
=
∆
δ
(5.217)
where
δ
δ
sin
-
cos
])([
bq
ed
dq
eq
b
ddqq
Vi
xx
xx
xx
V
ixxea
+
′
′
+
+
′
−+
′
= (5.218)
q
ed
eq
i
xx
xx
b
+
′
+
=
(5.219)

SYNCHRONOUS MACHINES
5-46
Substituting (5.215) into (5.212), we obtain
q
q
edc
dt
ed
′
∆−∆−=
′
∆
δ
(5.220)
where
δ
sin
1
b
ed
dd
do
V
xx
xx
T
c
+
′
′
−
′
=
(5.221)
and
ed
ed
do
xx
xx
T
d
+
′
+
′
=
1
(5.222)
Note that in the expressions for a, b, etc.
dq
ie ,
′
, etc. are values at the steady-state operating point.
Therefore, the expression for a can also be written as
δ
δ
sin
-
cos
])([
bq
ed
dq
eq
b
dqdfd
Vi
xx
xx
xx
V
ixxEa
+
′
′
+
+
−−= (5.223)
Similarly, the expression for i
d
for the initial steady-state value can also be written as
ed
b
ed
fd
d
xx
V
xx
E
i
+
−
+
=
δ
cos
(5.224)
Equations (5.213) and (5.220) can be written in state space form as
′
∆
∆
∆
−−
−−=
′
∆
∆
∆
qq
e
dc
ba
e
ω
δ
ωω
ω
δ
2H2H
1
oo
&
&
&
(5.225)
The characteristic equation is
0)(
2H2H
oo
23
=−+++ bcadad
ω
λ
ω
λλ
Applying Routh-Hurwitz criterion (see Appendix B), for stability, d > 0, a > 0, ad
− bc > 0 and
ad
− (ad − bc) > 0 or bc > 0. Note that the first and fourth conditions are always satisfied since b
> 0, c > 0 and d > 0. The third condition implies that a > 0.
From (5.219) and (5.221) – (5.223)
δ
δ
δ
sin
)(
))((
1
sin
-
cos
])([
1
2
bq
ed
ddeq
do
bq
ed
dq
eq
b
dqdfd
ed
ed
do
Vi
xx
xxxx
T
Vi
xx
xx
xx
V
ixxE
xx
xx
T
bcad
+
′
′
−+
′
−
+
′
′
+
+
−−
+
′
+
′
=−
Substituting the expressions for i
d
and i
q
from (5.224) and (5.211), the above reduces to
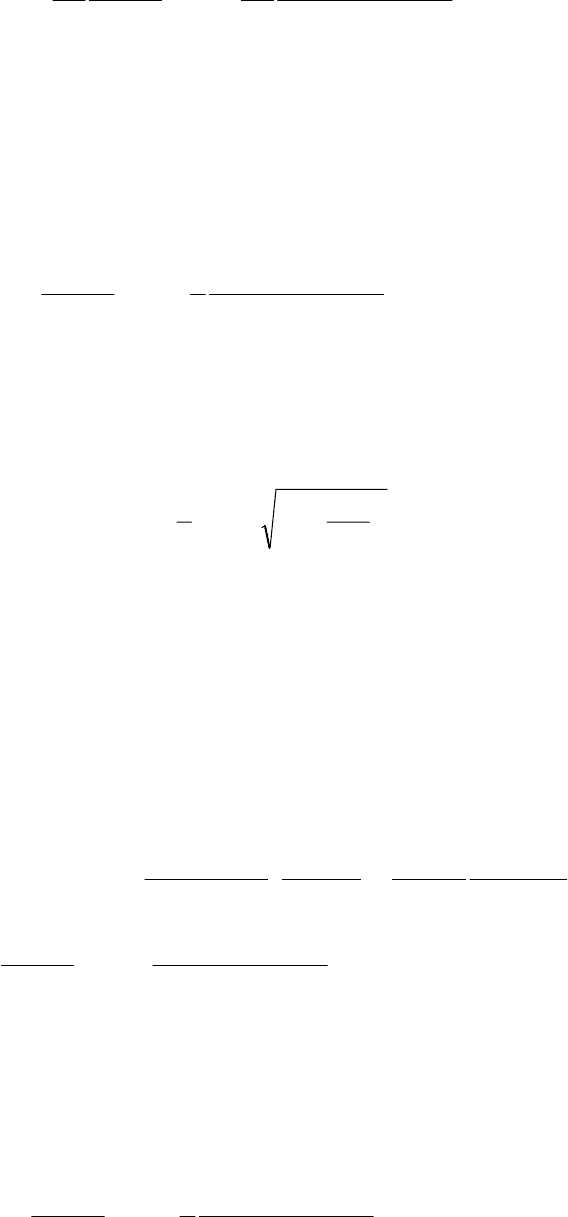
SYNCHRONOUS MACHINES
5-47
δδ
2cos
))((
1
cos
1
2
b
eqed
qd
doed
bfd
do
V
xxxx
xx
Txx
VE
T
bcad
++
′
−
′
+
+
′′
=−
(5.226)
At stability limit ad
− bc = 0. Therefore, from (5.226), when x
d
= x
q
, , stability limit is reached
when
δ
= 90°. For x
d
≠ x
q
(i.e., when saliency is present) stability limit is reached before
δ
reaches 90
°.
Power output at a specified
δ
for constant field voltage (steady-state power) is obtained, first by
rewriting (5.205) as
qdqdfde
iixxEP ])([
−
−=
, and then substituting for i
d
and i
q
from (5.224)
and (5.211) respectively, as
δδ
2sin
))((2
1
sin
2
b
eqed
qd
ed
bfd
e
V
xxxx
xx
xx
VE
P
++
−
+
+
= (5.227)
Maximum power is reached at
δ
< 90°.
Small disturbance stability performance can be assessed from the roots of the characteristic
equation. An analytical solution for the roots is not possible. However, we can obtain the roots at
the stability limit, when ad
− bc = 0. The roots are
−±−==
add
H
2
2
1
,0
o
2
3,21
ω
λλ
from which we can conclude that there is some damping due to the demagnetizing effect of
armature reaction, since no damping term was included in the swing equation (5.204). (Recall
that with constant-voltage-behind-reactance model, with no damping term present, the response
is oscillatory at constant amplitude.)
Excitation control helps counteract the demagnetizing effect of armature reaction. If we assume
that due to the action of excitation control field flux linkage is maintained constant, i.e.,
0
≡
′
∆
q
e
,
stability limit will be reached when a = 0.
Substituting for i
d
and i
q
from (5.210) and (5.211) into (5.218)
eq
b
ed
dq
eq
b
ed
bq
dqq
xx
V
xx
xx
xx
V
xx
Ve
xxea
++
′
′
−
+
+
+
′
−
′
′
−+
′
=
δδ
δ
22
sincos
cos
)(
δδ
2cos
))((
cos
2
b
eqed
dq
ed
bq
V
xxxx
xx
xx
Ve
++
′
′
−
−
+
′
′
=
(5.228)
Thus, excitation control can extend stability limit to
δ
well over 90°. However, excitation control
while extending the stability limit can also introduce negative damping. This is discussed in
more detail in the next chapter using the concepts of synchronizing and damping torque.
Power output at a specified
δ
for constant field flux linkage is obtained by substituting for i
d
and
i
q
from (5.210) and (5.211) into (5.205). Thus
δδ
2sin
))((2
1
sin
2
b
eqed
dq
ed
bq
e
V
xxxx
xx
xx
Ve
P
++
′
′
−
−
+
′
′
=
(5.229)

SYNCHRONOUS MACHINES
5-48
Maximum power is reached at
δ
> 90°.
Reactive power limit at P = 0
Reactive power limit at P = 0 is obtained by setting
δ
= 0. With
δ
= 0,
2
))((
11
b
eqed
qd
doed
bfd
do
V
xxxx
xx
Txx
VE
T
bcad
++
′
−
′
+
+
′′
=−
At stability limit ad
− bc = 0, or
0=
+
−
+
b
eq
qd
fd
V
xx
xx
E
(5.230)
From (5.224), with
δ
= 0,
ed
bfd
d
xx
VE
i
+
−
=
, or
)(
eddbfd
xxiVE
+
+
= (5.231)
From (5.230) and (5.231)
eq
b
d
xx
V
i
+
−=
, or
eq
b
xx
V
Q
+
=
2
lim
(leading) (5.232)
Self Excitation
Under certain conditions generator rotor flux-linkages can build up to excessive levels causing
severe overvoltage. This form of instability is known as self excitation. Self excitation can only
occur when capacitance is present in the circuit; for example, when machines are left connected
to open transmission lines or when lines are terminated by capacitors. In order to illustrate the
phenomenon, consider the system shown in Figure 5.11.
Fig. 5.11 A synchronous machine connected to a capacitive load.
Using the synchronous machine model 2, we have
qdddfdqdo
eixxEe
dt
d
T
′
−
′
−−=
′′
)( (5.233)
dqqqdqo
eixxe
dt
d
T
′
−
′
−=
′′
)( (5.234)
qqdd
ixee
′
+
′
=
(5.235)
ddqq
ixee
′
−
′
=
(5.236)
