Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.


3.3. Пример алгоритма покадровой анимации 81
Следовательно, декартовы координаты четвертой вершины D
8
в восьмом
кадре таковы: D
8
(−0.6, 1.4). Окончательно, координаты вершин квадрата в
восьмом кадре:
A
8
(−1, 1.4) ,B
8
(−1, 1.8) ,C
8
(−0.6, 1.8) ,D
8
(−0.6, 1.4) .
9-й кадр
Здесь сначала происходит смещение плоскости на вектор b =(−4, −4) для
совмещения центра исходного квадрата с началом координат. Затем плос-
кость равномерно масштабируется с коэффициентом 0.1. После этого плос-
кость смещается на вектор b
9
:
b
9
= −b +
9
10
· a =(4, 4) +
9
10
(−6, −3) = (−1.4, 1.3) .
Следовательно, оператор η
9
, который действует в девятом кадре, обладает
следующей матрицей:
η
9
= T
b
9
S
0.1
T
b
=
=
10−1.4
01 1.3
00 1
0.100
00.10
001
10−4
01−4
00 1
=
=
0.10−1.8
00.10.9
00 1
.
При помощи матричного умножения вычислим координаты вершин квад-
рата в девятом кадре:
A
9
= η
9
(A)=
0.10−1.8
00.10.9
00 1
3
3
1
=
−1.5
1.2
1
.
Следовательно, декартовы координаты первой вершины A
9
в девятом кадре
таковы: A
9
(−1.5, 1.2). Аналогично поступим со второй вершиной:
B
9
= η
9
(B)=
0.10−1.8
00.10.9
00 1
3
5
1
=
−1.5
1.4
1
.
Следовательно, декартовы координаты второй вершины B
9
в девятом кадре
таковы: B
9
(−1.5, 1.4). Далее — аналогично поступим с третьей вершиной:
C
9
= η
9
(C)=
0.10−1.8
00.10.9
00 1
5
5
1
=
−1.3
1.4
1
.
Следовательно, декартовы координаты третьей вершины C
9
в девятом кад-
ре таковы: C
9
(−1.3, 1.4). Далее — аналогично поступим с четвертой верши-
ной:
D
9
= η
9
(D)=
0.10−1.8
00.10.9
00 1
5
3
1
=
−1.3
1.2
1
.

82 Глава 3. Проективные операторы
Следовательно, декартовы координаты четвертой вершины D
9
в девятом
кадре таковы: D
9
(−1.3, 1.2). Окончательно, координаты вершин квадрата в
девятом кадре:
A
9
(−1.5, 1.2) ,B
9
(−1.5, 1.4) ,C
9
(−1.3, 1.4) ,D
9
(−1.3, 1.2) .
10-й кадр
Здесь сначала происходит смещение плоскости на вектор b =(−4, −4) для
совмещения центра исходного квадрата с началом координат. Затем плос-
кость равномерно масштабируется с коэффициентом 0. После этого плос-
кость смещается на вектор b
10
:
b
10
= −b +
10
10
· a =(4, 4) + (−6, −3) = (−2, 1) .
Следовательно, оператор η
10
, который действует в десятом кадре, обладает
следующей матрицей:
η
10
= T
b
10
S
0
T
b
=
=
10−2
01 1
00 1
000
000
001
10−4
01−4
00 1
=
=
00−2
00 1
00 1
.
При помощи матричного умножения вычислим координаты вершин квад-
рата в десятом кадре:
A
10
= η
10
(A)=
00−2
00 1
00 1
3
3
1
=
−2
1
1
.
Следовательно, декартовы координаты первой вершины A
10
в десятом кад-
ре таковы: A
10
(−2, 1). Аналогично поступим со второй вершиной:
B
10
= η
10
(B)=
00−2
00 1
00 1
3
5
1
=
−2
1
1
.
Следовательно, декартовы координаты второй вершины B
10
в десятом кад-
ре таковы: B
9
(−2, 1). Далее — аналогично поступим с третьей вершиной:
C
10
= η
10
(C)=
00−2
00 1
00 1
5
5
1
=
−2
1
1
.
Следовательно, декартовы координаты третьей вершины C
10
в десятом кад-
ре таковы: C
10
(−2, 1). Далее — аналогично поступим с четвертой вершиной:
D
10
= η
10
(D)=
00−2
00 1
00 1
5
3
1
=
−2
1
1
.
3.3. Пример алгоритма покадровой анимации 83
Следовательно, декартовы координаты четвертой вершины D
10
в десятом
кадре таковы: D
10
(−2, 1). Окончательно, координаты вершин квадрата в
десятом кадре совпадают друг с другом:
A
10
(−2, 1) ,B
10
(−2, 1) ,C
10
(−2, 1) ,D
10
(−2, 1) .
x
y
0
A
B
C
D
H = A
10
= B
10
= C
10
= D
10
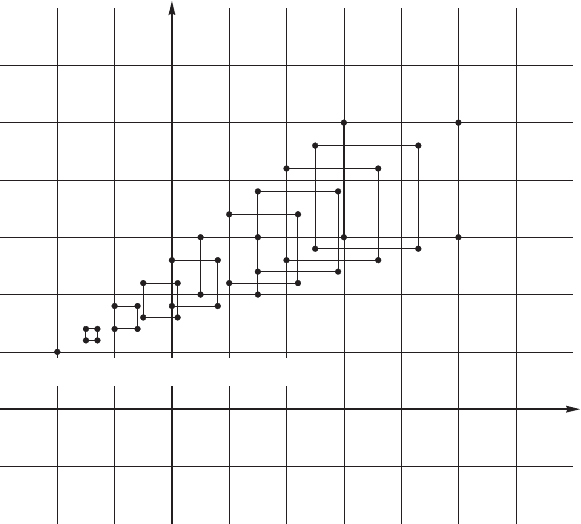
Рис. 3.6: Десять кадров анимации.
84 Глава 3. Проективные операторы
Часть II
Плоские кривые
85

Глава 4
Криволинейные траектории
Нетрудно передать процессору алгоритм построения прямой. Действитель-
но, прямая может интерпретироваться как график линейной функции, и
вычисление координат любой ее точки не составляет труда. На этом осно-
ван метод аппроксимации криволинейных траекторий, когда кривая при-
ближенно заменяется многозвеньевой ломаной, визуально неотличимой от
исходной кривой.
Однако часто бывает необходимо иметь точное описание кривой (например,
если кривая должна произвольно масштабироваться). В этом случае про-
изводится интерполяция кривой по набору исходных данных: точкам, через
которые она проходит, направлениям прохождения и т. д.
В этой главе мы рассмотрим методы описания кривых (см. раздел 4.1,
стр. 87) и классифицируем задачи интерполяции кривых (см. раздел 4.2,
стр. 91)
4.1 Различные способы задания кривых
Везде в пределах второй части книги мы будем считать, что на плоскости
π (или в физическом пространстве R
3
) фиксирована прямоугольная си-
стема координат
1
. Связывая переменные соотношениями (непосредственно
или опосредованно при промощи вспомогательного параметра), мы можем
получить описание любой кривой или любой поверхности.
Определение 34 (уравнение кривой) Пусть на плоскости π фиксиро-
вана прямоугольная система координат xOy. И пусть переменные x и y
связаны соотношением:
F (x, y)=0.
Тогда множество точек плоскости π, координаты которых удовлетворяют
этому уравнению, образуют на плоскости некоторую кривую C. Уравнение
1
С точки зрения линейной алгебры, средствами которой мы пользовались в первой
части, это означает, что на плоскости фиксирован ортонормированный базис. Это вполне
согласуется с результатами, полученными в третьей главе: мы уже тогда предполагали
наличие именно ортонормированного базиса на плоскости и в объемлющем пространстве.
87
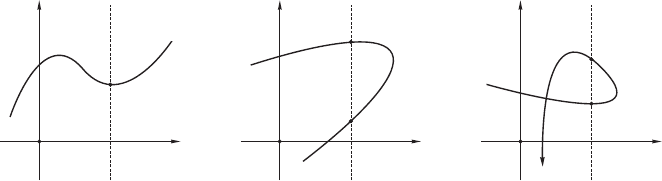
88 Глава 4. Криволинейные траектории
F (x, y)=0называется уравнением кривой C. Это обозначается следующим
образом:
C : F (x, y)=0.
Пример 55 Уравнение x +y =0описывает на плоскости прямую, x
2
+ y
2
−1=0
— единичную окружность, y − e
x
=0— экспоненциальную кривую и т. д.
Определение 35 (явные и неявные уравнения кривых) Допустим,
кривая C описывается при помощи некоторого уравнения
C : F (x, y)=0.
Оно называется неявным уравнением кривой C, если из него невозможно
выразить одну переменную через другую. Если же такое выражение воз-
можно, то уравнение приобретает вид:
C : y = f(x) .
Такое уравнение называется явным уравнением кривой C.
Кривые, описанные неявными уравнениями, образуют более широкий класс
кривых, нежели кривые, описанные при помощи явных уравнений. Дей-
ствительно, из определения следует, что явное уравнение кривой есть част-
ный случай неявного уравнения. Так, например, если уравнение допускает
явное выражение переменной y через переменную x, то кривая, отвечающая
уравнению
C : y = f(x) ,
является графиком функции f(x) и характеризуется тем, что любая вер-
тикальная прямая пересекает ее не более, чем в одной точке. Вместе с
тем, неявные кривые допускают множественное пересечение вертикальны-
ми прямыми, например — окружность x
2
+ y
2
=1может пересекаться вер-
тикальными пямыми в двух точках.
x
y
0
y = f(x)
(a) Явная кривая.
x
y
0
F (x, y)=0
(b) Неявная кривая.
x
y
0
p(u)
(c) Параметрическая кри-
вая.
Рис. 4.1: Различные способы задания кривых.
Определение 36 (параметрические уравнения кривой) Пусть p(u) —
функция, аргументом которой служит число, а в качестве значения она
принимает вектор
p
1
(u)
p
2
(u)
,
4.1. Различные способы задания кривых 89
где p
1
(u), p
2
(u) — явные функции переменной u. Такая функция называ-
ется параметрической (или — векторнозначной). Если параметр u пробега-
ет значения из интервала [u
1
,u
2
] то вектор p(u) при этом описывает дугу
некоторой прямой на плоскости. Эта кривая называется параметрически
заданной плоской кривой.
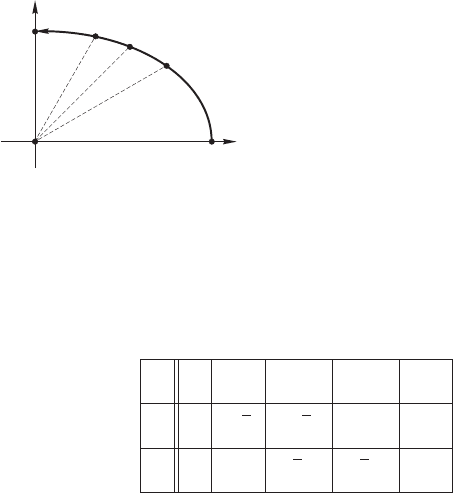
Пример 56 Рассмотрим следующую функцию, заданную параметрически:
u =0
u = π/6
u = π/4
u = π/3
u = π/2
x
y
0
Рис. 4.2: Дуга эллипса.
p(u)=
2cosu
sin u
,u∈ [0,π/2] .
Она описывает некоторую кривую, точки
которой удовлетворяют ее координатным
функциям.
Последовательно придавая некоторые, хо-
рошо известные из элементарной тригоно-
метрии частные значения парметру u,вы-
числим декартовы координаты x и y вектора p(u).
Эта процедура отличается от привычного вычисления значения функции по зна-
чению переменной лишь тем, что в качестве независимой переменной здесь вы-
ступает параметр u, а вычисляемыми являются функции x и y.
u 0 π/6 π/4 π/3 π/2
x 2
√
3
√
2 1 0
y 0 1/2
√
2/2
√
3/2 1
Соединим полученные точки плавной линией и получим дугу эллипса, располо-
женную в первой четверти (см. рис. 4.2, стр. 89).
Любую явную кривую можно параметризовать тривиальным образом. Дей-
ствительно, если
y = f(x) ,
то тогда, полагая в качестве первой параметризующей функции параметр
u, а в качестве второй — функцию f(u), получим:
p(u)=
u
f(u)
.
Следовательно, парметрические кривые, так же как и неявные, обобщают
класс явных кривых.
Однако нельзя утверждать, что параметрические кривые обобщают класс
неявных кривых (в ряде случаев параметризацию неявной кривой устроить
можно, а в других — нет).
Тем не менее, параметрические кривые окажутся для наших целей наиболее
подходящим инструментом, что демонстрирует следующий пример.
90 Глава 4. Криволинейные траектории
Пример 57 Рассмотрим единичную окружность. Мы можем описать ее неявно:
x
2
+ y
2
=1.
С другой стороны, эту же самую кривую мы можем параметризовать:
p(u)=
cos u
sin u
.
Нетрудно убедиться, что эта парметризация действительно описывает то же са-
мое геометрическое множество, что и неявное уравнение единичной окружности.
Действительно, декартовы координаты вектора p(u) таковы:
x =cosu,
y =sinu.
Возведем обе части обоих уравнений в квадрат и сложим результаты:
x
2
+ y
2
=cos
2
u +sin
2
u, откуда x
2
+ y
2
=1.
Вместе с тем, между неявной и параметрической записями есть существенная
разница. Дело в том, что, параметризуя окружность, мы не указали промежуток
изменения параметра u, а это значит, что окуржность, описанная параметрически
(в отличие от окружности, описанной неявно), состоит из бесконечного числа
витков.
Более того, если даже мы сузим параметрическую окружность до одного вит-
ка, указав промежуток изменения параметра u ∈ [0, 2π], то результат все равно
будет отличаться от окружности, описанной неявно: в параметрическом случае
окружность обладает динамикой, имеются стартовая точка и конечная, имеется
направление обхода.
Таким образом, если требуется описать не просто геометрическое место то-
чек на плоскости, но траекторию движения, то параметрическая форма
записи оказывается явно предпочтительнее.
Имеется еще один аспект, определяющий предпочтительность параметри-
ческого варианта описания кривых. Он связан с обобщением понятия тра-
ектории с плоского случая на пространственный.
Аналитически (то есть при помощи явных или неявных уравнений) описать
кривую в трехмерном пространстве можно только в виде системы. Действи-
тельно, при помощи одного уравнения
F (x, y, z)=0
описывается поверхность. Аналогично можно описать еще одну поверх-
ность:
G(x, y, z)=0.
Их пересечение есть кривая. Она описывается как решение системы урав-
нений:
F (x, y, z)=0,
G(x, y, z)=0.
Мало того, что такое описание является очень громоздким, следует также
иметь в виду, что не существует универсального алгоритма решения таких
