Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

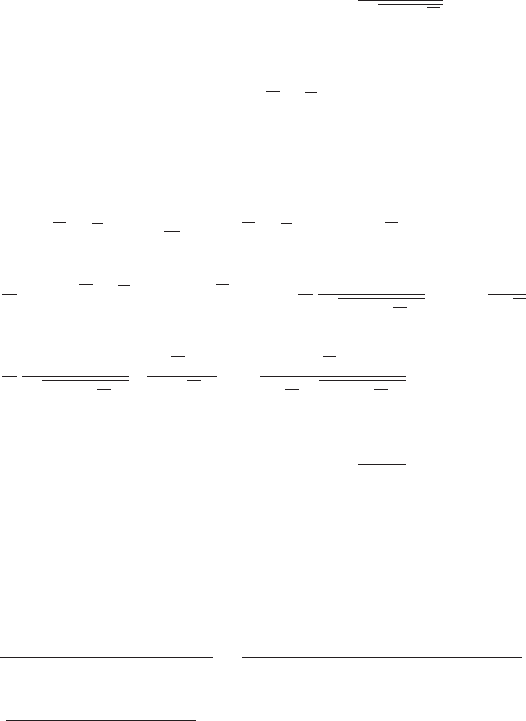
C.1. Дифференцирование функций 211
Пример 152 Продифференцировать функцию y =
1
3
x +
√
x
.
Прежде всего, преобразуем функцию, чтобы избавиться от использования ради-
калов в ее записи.
y =
x +
√
x
−
1
3
.
Теперь дифференцируемая функция — это сложная функция, у которой внешняя
функция является степенной, а внутренняя — суммой двух элементарных (также
степенных) функций. Поэтому:
y
=
x +
√
x
−
1
3
= −
1
3
x +
√
x
−
1
3
−1
·
x +
√
x
=
= −
1
3
x +
√
x
−
4
3
·
x
+(
√
x )
= −
1
3
1
3
(x +
√
x )
4
·
1+
1
2
√
x
=
= −
1
3
1
3
(x +
√
x )
4
·
2
√
x +1
2
√
x
= −
2
√
x +1
6
√
x
3
(x +
√
x )
4
.
Пример 153 Продифференцировать функцию y =
e
2x
cos 3x
.
Данная функция — это частное двух функций, каждая из которых является слож-
ной (так же, как и в примере 151). Поэтому, прежде всего, применим правило
дифференцирования частного (теор. 97, стр. 206), а уже затем ко всем остав-
шимся производным — правило дифференцирования сложной функции (теор. 98,
стр. 208):
y =
e
2x
cos 3x − e
2x
(cos 3x)
cos
2
3x
=
e
2x
(2x)
cos 3x − e
2x
(−sin 3x)(3x)
cos
2
3x
=
=
2e
2x
cos 3x +3e
2x
sin 3x
cos
2
3x
.
Пример 154 Пусть требуется вычислить производную функции y при конкрет-
ном значении переменной x:
y = e
3x
cos 5x, при x =0.
Прежде всего, продифференцируем данную функцию, пользуясь правилами диф-
ференцирования (теор. 97, стр. 206 и теор. 98, стр. 208):
y
=(e
3x
)
cos 5x + e
3x
(cos 5x)
= e
3x
(3x)
cos 5x + e
3x
(−sin 5x)(5x)
=
=3e
3x
cos 5x − 5e
3x
sin 5x.
Теперь в найденную функцию y
мы можем в качестве аргумента подставить x =0
и получить результат:
y
(0) = 3e
0
cos 0 − 5e
0
sin 0 = 3 · 1 · 1 − 5 · 1 · 0=3.
Итак, значение производной при фиксированном значении переменной — это кон-
кретное число (в данном случае y
(0) = 3).

212 Приложение C. Функции и графики
C.1.3 Дифференцирование функции, заданной
параметрически
Дифференцирование функций, заданных параметрически, сводится к дифферен-
цированию явных функций (см. опр. 60, стр. 132). В этом разделе мы разберем
несколько примеров такого дифференцирования.
Определение 86 (производная параметрической функции) Пусть имеет-
ся функция, заданная параметрически при помощи параметра u:
p(u)=
p
1
(u)
p
2
(u)
; u ∈ [α
1
; α
2
]
Пусть функции p
1
(u) и p
2
(u) являются дифференцируемыми на отрезке [α
1
; α
2
]
как функции переменной u. Тогда производной параметрически заданной функ-
ции p(u) называется параметрически заданная функция p
(u), определенная сле-
дующим образом
1
:
p
(u)=
p
1
(u)
p
2
(u)
; u ∈ [α
1
; α
2
]
Пример 155 Вычислить производную функции, заданной параметрически:
p(u)=
u(1 −sin u)
u cos u
.
Согласно определению (опр. 86), нам достаточно по отдельности продифферен-
цировать координаты функции p(u):
p
1
(u)=
u(1 −sin u)
= u
· (1 − sin u)+u ·(1 − sin u)
=
=1· (1 − sin u)+u ·(0 − cos u)=1− sin u − u cos u,
p
2
(u)=
u cos u
= u
· cos u + u ·(cos u)
=
=1· cos u + u ·(−sin u)=cosu − u sin u.
Таким образом, производная данной параметрически заданной функции — это
следующий вектор:
p
(u)=
1 −sin u − u cos u
cos u − u sin u
.
Пример 156 Продифференцировать функцию, заданную параметрически:
p(u)=
e
u
cos u
e
u
sin u
.
Задача решается агналогично предыдущей. Все, что от нас требуется, — это про-
дифференцировать координаты p
1
(u) и p
2
(u).
p
1
(u)=
e
u
cos u
=(e
u
)
· cos u + e
u
· (cos u)
=
= e
u
· cos u + e
u
· (−sin u)=e
u
cos u − e
u
sin u,
p
2
(u)=
e
u
sin u
=(e
u
)
· sin u + e
u
· (sin u)
=
= e
u
· sin u + e
u
· cos u = e
u
sin u + e
u
cos u.
1
В большинстве учебников принято другое определение производной функции, задан-
ной параметрически. Такая функция связывает независимые переменные x и y опосре-
довано через параметр u, и обычно под производной такой функции понимают именно
производную функции y по переменной x. Особенность нашего определения состоит в
том, что мы дифференцируем функцию по параметру u, а не по одной из переменных.
C.2. Касательные к кривым 213
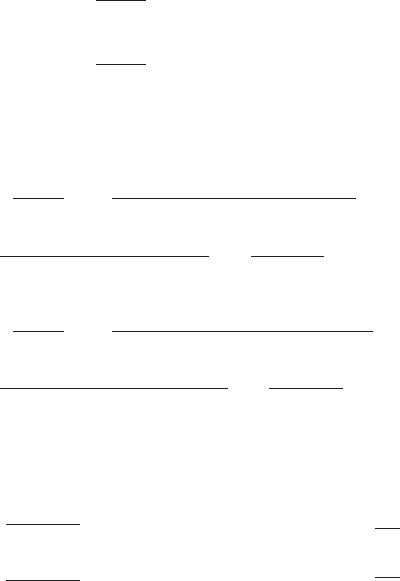
Ответом в этой задаче служит следующая функция:
p
(u)=
e
u
cos u − e
u
sin u
e
u
sin u + e
u
cos u
.
Пример 157 Вычислить значение производной функции p(u), заданной пара-
метрически, при указанном значении параметра u:
p(u)=
3u
1+u
2
3u
2
1+u
2
при u =2.
Прежде всего, вычислим функцию, являющуюся производной функции p(u).Для
этого (так же, как и выше) продифференцируем ее координаты.
p
1
(u)=
3u
1+u
2
=
(3u)
· (1 + u
2
) −3u · (1 + u
2
)
(1 + u
2
)
2
=
=
3 ·(1 + u
2
) −3u · (0 + 2u)
(1 + u
2
)
2
=3
1 −u
2
(1 + u
2
)
2
,
p
2
(u)=
3u
2
1+u
2
=
(3u
2
)
· (1 + u
2
) −3u
2
· (1 + u
2
)
(1 + u
2
)
2
=
=
6u ·(1 + u
2
) −3u
2
· (0 + 2u)
(1 + u
2
)
2
=6
u
(1 + u
2
)
2
.
Таким образом, производная функции p(u) — это следующая параметрически за-
данная функция:
p
(u)=
3
1 −u
2
(1 + u
2
)
2
6
u
(1 + u
2
)
2
, при этом
p
1
(2) = −
9
25
,
p
2
(2) =
12
25
.
Следовательно, искомое значение производной (при u =2) — это вектор с число-
выми координатами −9/25 и 12/25:
p
(2) = (−9/25; 12/25) .
C.2 Касательные к кривым
Геометрический смысл производной функции (заданной как явно, так и парамет-
рически) в той или иной форме приводит к понятию касательной к кривой (ка-
сательной прямой к графику функции, заданной явно, или касательного вектора
к кривой, описанной параметрически). В этом разделе мы рассмотрим задачи
описания касательных.
Теоретический материал, относящийся к данному разделу, представлен выше (см.
раздел 5.3, стр. 133).
214 Приложение C. Функции и графики
C.2.1 Уравнение касательной к графику явной функ-
ции
Производная функции характеризует ее поведение в окрестности точки: чем боль-
ше производная, тем быстрее возрастает функция, и наоборот. В этом состоит ее
геометрический смысл, утверждение, доказанное нами выше, в пределах теоре-
тического блока (см. теор. 76, стр. 133), которое мы продублируем здесь ради
удобства изучения материала.
Теорема 99 (геометрический смысл производной) Пусть функция y = f (x)
дифференцируема в точке x
0
. Тогда значение производной y
(x
0
) функции y в
точке x
0
равно тангенсу угла наклона касательной к графику функции y = f (x),
проведенной в точке x
0
(или, что то же самое, равно угловому коэффициенту k
касательной y = kx + b к графику функции y = f(x) в точке x
0
).
Как следствие, из геометрического смысла производной вытекает следующее утвер-
ждение (его доказательство см. выше: теор. 77, стр. 134).
Теорема 100 ( уравнение касательной к явной кривой) Допустим, функ-
ция y = f(x) дифференцируема в точке x
0
. Тогда касательная l к соответствую-
щей явной кривой y = f(x), проведенная в точке с абсциссой x
0
, имеет следующее
уравнение:
l : y = f(x
0
)+f
(x
0
)(x −x
0
) .
Пример 158 Записать уравнение касательной к графику функции y = x
2
в точ-
ке с абсциссой x
0
=2.
Воспользуемся соответствующей теоремой (теор. 100, стр. 214) для того, чтобы
записать уравнение:
l : y = f(x
0
)+f
(x
0
)(x −x
0
)=x
2
0
+2x
0
(x −x
0
)=2
2
+4(x − 2) = 4x − 4 .
Таким образом, интересующая нас касательная имеет уравнение: y =4x − 4.
Пример 159 Записать уравнение касательной к графику функции y =5sin4x в
точке с абсциссой x
0
= π/4.
Поступим так же, как и в предыдущем примере (теор. 100, стр. 214):
l : y = f(x
0
)+f
(x
0
)(x −x
0
)=5sin(4x
0
) + 20 cos(4x
0
)(x −x
0
)=
=5sin(4π/4) + 20 cos(4π/4)(x − π/4) = 20(x − π/4) = 20x − 5π.
Следовательно, уравнение касательной следующее: y =20x − 5π.
C.2.2 Уравнение касательной к кривой, описанной па-
раметрически
Результаты, которые мы используем в этом разделе, были получены во второй
части книги (см. раздел 5.3.2, стр. 135). Здесь мы продублируем нужные нам
утверждения и рассмотрим примеры.
Прежде, чем обратиться к параметирически заданным кривым, дадим еще один
способ описания прямой. А именно: зная точку A(x
A
,y
A
), через которую проходит
прямая l, и зная вектор a = {a
1
,a
2
}, которому прямая l параллельна (то есть —
направляющий вектор прямой l), можно получить уравнение этой прямой в так
называемой канонической форме.
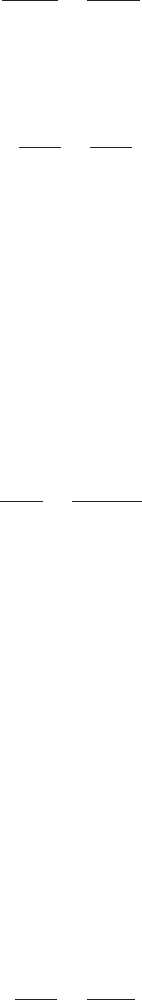
C.2. Касательные к кривым 215
Теорема 101 (каноническое уравнение прямой) Пусть прямая l проходит
через точку A(x
A
,y
A
) параллельно вектору a = {a
1
,a
2
}. Тогда ее уравнение мо-
жет быть записано в канонической форме следующим образом:
l :
x −x
A
a
1
=
y − y
A
a
2
.
Пример 160 Записать уравнение прямой l, проходящей через точку (2, 3) вна-
пралении вектора {−1, 4}.
Воспользуемся теоремой о каноническом уравнении прямой (теор. 101, стр. 215):
l :
x −2
−1
=
y − 3
4
— уравнение в канонической форме получено. Пользуясь свойствами пропорций,
можно легко свести это уравнение к традиционному виду:
l :4(x − 2) = −(y − 3) , откуда l : y = −4x +11.
Пример 161 Записать уравнение прямой, проходящей через две данные точки:
A(2, −1) и B(4, 3).
Здесь в качестве направляющего вектора можно выбрать вектор AB (действи-
тельно, он лежит на прямой l, а следовательно, он ей параллелен), а в качестве
точки, через которую проходит прямая, можно выбрать любую из точек A или B
(для определенности — возьмем точку A). Тогда, так как координаты вектора AB
—это{4 − 2, 3 − (−1)} = {2, 4}, то, согласно теореме о каноническом уравнении
прямой (теор. 101, стр. 215), получим:
l :
x −2
2
=
y − (−1)
4
.
Пользуясь свойствами пропорций, это уравнение можно преобразовать к тради-
ционной форме:
l :4(x − 2) = 2(y +1), откуда l : y =2x − 3 .
Отметим одно очень важное качество канонических уравнений: они позволяют
описывать прямые, проходящие во всех направлениях, в том числе — и верти-
кальные (что невозможно сделать в явной форме: ведь при этом угловой коэф-
фициент прямой становится бесконечным). Следует иметь ввиду, что при этом
в знаменателях канонических уравнений обязательно будут появляться нули. В
этом нет никакого противоречия (хотя, казалось бы, на ноль делить нельзя), так
как канонические уравнения следует рассматривать именно как пропорции.
Пример 162 Записать уравнение прямой l, проходящей через точку (2, 1) вер-
тикально.
Направляющий вектор вертикальной прямой тоже вертикален, то есть — его пер-
вая координата должна равняться нулю. Вторая координата может быть любой
(вектор все равно останется вертикальным), пусть она равна 1. Итак, прямая l
проходит через точку (2, 1) в направлении вектора {0, 1}:
l :
x −2
0
=
y − 1)
1
Воспользуемся свойствами пропорций для перехода к явному уравнению каса-
тельной:
l :1(x − 2) = 0(y +1), откуда l : x =2.

216 Приложение C. Функции и графики
Мы видим, что явное уравнение вертикальной прямой не содержит вертикальной
переменной. Это можно содержательно интерпретировать так: горизонтальная
переменная из этого уравнения тождественно равна какой-то константе (в данном
случае — 2), а вертикальная может изменяться произвольно. Множество точек
плоскости, координаты которых удовлетворяют этим требованиям, — это и есть
вертикальная прямая.
Отметим здесь же, что, по тем же самым соображениям, явное уравнение гори-
зонтальной прямой не содержит горизонтальной переменной.
Теорема 102 (производная параметрически заданной функции) Пусть
функция
p(u)=
p
1
(u)
p
2
(u)
дифференцируема при u = u
0
. Тогда вектор p
(u
0
) — это в точности направляю-
щий вектор для прямой, касательной к кривой p(u) в точке (p
1
(u
0
),p
2
(u
0
)).
Теорема 103 ( уравнение касательной к параметрической кривой )
Пусть функция
p(u)=
p
1
(u)
p
2
(u)
дифференцируема при u = u
0
. Тогда касательная l к кривой p(u), проведенная к
ней в точке (p
1
(u
0
),p
2
(u
0
)), описывается канонически следующим уравнением:
l :
x −p
1
(u
0
)
p
1
(u
0
)
=
y − p
2
(u
0
)
p
2
(u
0
)
.
Пример 163 Составить уравнение касательной к данной линии p(u) при указан-
ном значении параметра u:
p(u)=
2lnctgu +1
tg u +ctgu
при u = π/4 .
Для составления уравнения касательной нам необходимо знать (см. теор. 101,
стр. 215) координаты точки, через которую касательная проходит, и координа-
ты направляющего вектора, которому касательная параллельна. Прежде всего —
вычислим направляющий вектор p
(π/4) касательной l. Для этого (см. теор 103,
стр. 216) подсчитаем производную p
(u):
p
1
(u)=(2lnctgu +1)
=2· (ln ctg u)
=2·
1
ctg u
·
−
1
sin
2
u
= −
2
sin u cos u
=
= −
4
sin 2u
p
2
(u) = (tg u +ctgu)
= (tg u)
+(ctgu)
=
1
cos
2
u
−
1
sin
2
u
= −4
cos
2
2u
sin
2
2u
.
Подставляя на место u конкретное значение u = π/4, найдем координаты каса-
тельного вектора:
p
1
(π/4) = −
4
sin π/2
= −4 ,
p
2
(π/4) = −4
cos
2
π/2
sin
2
π/2
=0.
Следовательно, касательный вектор — это вектор с координатами {−4, 0}.Далее
нам следует знать координаты точки, через которую проходит касательная. Это

C.2. Касательные к кривым 217
— точка на кривой, которой отвечает значение параметра u = π/4, то есть точка
p(π/4):
p
1
(π/4) = 2 ln ctg π/4+1=1,
p
2
(π/4) = tg π/4+ctgπ/4=2.
Итак, инетересующая нас касательная — это прямая, проходящая через точку
(1, 2) в направлении вектора {−4, 0}. Пользуясь теоремой о каноническом урав-
нении прямой (теор. 101, cтр. 215), запишем уравнение:
l :
x −1
−4
=
y − 2
0
.
При помощи свойств пропорций, преобразуем это уравнение к явному виду:
l :0·(x − 1) = −4 · (y − 2) , откуда l : y =2.
В этом случае касательная оказалась горизонтальной.
Пример 164 Пусть кривая p(u) описана параметрически уравнениями:
p(u)=
u −u
4
u
2
− u
3
,
Требуется описать касательную к этой кривой в точке (0, 0).
Прежде всего необходимо найти те значения параметра, при которых кривая p(u)
проходит через точку (0, 0). Это в точности то значение u, которое удовлетворяет
следующим условиям:
u −u
4
=0
u
2
− u
3
=0
отсюда
u(1 −u
3
)=0
u
2
(1 −u)=0
и, значит u
1
=0,u
2
=1.
Мы видим, что кривая p(u) проходит через точку (0, 0) дважды: при u =0и при
u =1. Это означает, что кривая терпит самопересечение в этой точке, и что скорее
всего в этой точке она обладает двумя касательными, причем эти касательные
различны.
Итак, найдем обе касательные к кривой p(u) в точке (0,0). Пусть сначала u =0.
Прежде всего, для нахождения касательного вектора нам необходимо вычислить
производную функции p(u) при u =0.
p
(u)=
1 −4u
3
2u −3u
2
поэтому p
(0) =
1
0
.
Теперь нам известен вектор, касательный к кривой p(u) в точке (0, 0) при u =0.
Он же является направляющим вектором касательной прямой, проходящей через
точку (0, 0). Согласно теореме об уравнении прямой (теор. 101, стр. 215) мы можем
записать каноническое уравнение касательной:
l
1
:
x −0
1
=
y − 0
0
, откуда l
1
: y =0.
Таким образом, одна из касательных (а именно, та из них, которая отвечает зна-
чению u =0) является горизонтальной прямой y =0.
Пусть теперь u =1. Для нахождения направляющего вектора касательной вы-
числим производную p
(u) при u =1:
p
(u)=
1 −4u
3
2u −3u
2
, поэтому p
(1) =
−3
−1
.

218 Приложение C. Функции и графики
Согласно теореме об уравнении прямой (теор. 101, стр. 215) записываем еще одно
каноническое уравнение касательной:
l
2
:
x −0
−3
=
y − 0
−1
, откуда l
2
: y =
1
3
x.
Следовательно, вторая касательная является наклонной прямой. Окончательно
имеем: кривая p(u) терпит в точке (0, 0) самопересечение и обладает двумя каса-
тельными:
l
1
: y =0,l
2
: y =
1
3
x.
C.3 Алгоритмы интерполяции
Формирование кривой по заданным начальным характеристикам, таким, как точ-
ки, через которые проходит кривая или направления ее прохождения, называется
интерполяцией кривой в той или иной форме.
Теоретические основы алгоритмов интерполяции были получены нами в заклю-
чительной главе книги (см. главу 6, стр. 139) и, по сути, служат кульминацией
курса.
В этом разделе мы рассмотрим два типа интерполирующих алгоритмов: точную
интерполяцию и интерполяцию в форме Эрмита.
C.3.1 Точная интерполяция
В этом разделе мы продублируем результаты, полученные нами выше в теорети-
ческом блоке (см. раздел 6.1, стр. 139) и разберем примеры.
Определение 87 (точная интерполяция) Пусть на плоскости π фиксирован
некоторый набор точек A
1
,...,A
n
, который мы будем называть опорным ансам-
блем. Точной интерполирующей кривой для данного ансабля называется кривая
C, проходящая через каждую точку ансамбля ровно по одному разу и в указанном
порядке.
Описание этой кривой в виде полиномиальной параметризации называется точной
интерполяцией данного ансамбля.
Теорема 104 (точная квадратичная интерполяция) Для любого опорного
ансамбля, состоящего из трех точек A(x
A
,y
A
), B(x
B
,y
B
), C(x
C
,y
C
) существу-
ет единственная точно интерполирующая его кривая, являющаяся квадратичной
параметризацией вида
p(u)=
a
10
+ a
11
u + a
12
u
2
a
20
+ a
21
u + a
22
u
2
,
причем коэффициенты параметризующих многочленов вычисляются однозначно,
исходя из координат точек опорного ансамбля:
a
10
a
11
a
12
=
100
−34− 1
2 −42
x
A
x
B
x
C
,
a
20
a
21
a
22
=
100
−34− 1
2 −42
y
A
y
B
y
C
.
Матрица, фигурирующая в вычислениях, называется квадратичной матрицей точ-
ной интерполяции.
C.3. Алгоритмы интерполяции 219
Пример 165 Найти точную итерполяцию ансамбля: A
1
(1, 1), A
2
(−2, 3), A
3
(2, 1).
Воспользуемся теоремой о матрице точной интерполяции (теор. 104, стр. 218).
Согласно этой теореме, мы можем выписать точную интерполирующую кривую
в виде
p(u)=
a
10
+ a
11
u + a
12
u
2
a
20
+ a
21
u + a
22
u
2
,
где коэффициенты параметризации находятся матричным умножением:
a
10
a
11
a
12
=
100
−34− 1
2 −42
1
−2
2
,
a
20
a
21
a
22
=
100
−34− 1
2 −42
1
3
1
при помощи матрицы точной интерполяции. Следовательно, коэффициенты па-
раметризации следующие:
a
10
a
11
a
12
=
1
−13
14
,
a
20
a
21
a
22
=
1
8
−8
,p(u)=
1 −13u +14u
2
1+8u − 8u
2
.
Выполним проверку. Кривая должна проходить через три опорные точки A
1
, A
2
,
A
3
равномерно, то есть при значениях параметра 0, 1/2 и 1 соответственно:
p(0) =
1
1
= A
1
,p(1/2) =
−2
3
= A
2
,p(1) =
2
1
= A
3
.
C.3.2 Интерполяция в форме Эрмита
Эрмитова интерполяция позволяет строить кривые по опорному ансамблю, со-
стоящему из произвольно большого числа точек, при этом (в отличие от точной
интерполяции) вычислительная сложность алгоритма не возрастает: все действия
выполняются при помощи многочленов третьей степени (см. раздел 6.2, стр. 143).
Это достигается за счет разбиения опорного ансамбля на сегменты, состоящие
всего из двух соседних точек, и требования гладкости сопряжения соседних сег-
ментов. Широко распространенный инструмент графических редакторов — так
называемая кривая Безье — формирует кривую именно по принципу эрмитова
алгоритма интерполяции.
В этом разделе мы продублируем полученные нами выше теоретические резуль-
таты и рассмотрим примеры.
Определение 88 (эрмитова интерполирующая кривая) Пусть на плоско-
сти π фиксированы две точки A(x
A
,y
A
) и B(x
B
,y
B
). Интерполирующей кривой
в форме Эрмита для опорного ансамбля, состоящего из этих точек, называется
кривая, стартующая в точке A в направлении данного вектора v =(x
v
,y
v
) ифи-
ниширующая в точке B в направлении еще одного данного вектора w =(x
w
,y
w
).
Теорема 105 (интерполяция в форме Эрмита) Пусть кривая p(u) стартует
в точке A(x
A
,x
B
) в направлении вектора v =(x
v
,y
v
) и финиширует в точке
B(x
B
,y
B
) в направлении вектора w =(x
w
,y
w
). Тогда существует единственная
кубическая параметризация этой кривой
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
220 Приложение C. Функции и графики
причем коэффициенты параметризующих многочленов вычисляются по следую-
щим формулам:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
x
A
x
B
x
v
x
w
,
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
y
A
y
B
y
v
y
w
.
Матрица, фигурирующая в вычислениях, называется матрицей Эрмита.
Пример 166 Пусть кривая p(u) проходит через точки A
1
(1, 1) и A
2
(2, 1) вна-
правлении векторов v
1
=(−1, 1) и v
2
=(1, −1). Требуется описать кривую p(u)
параметрически.
Задача решается при помощи теоремы об эрмитовой интерполяции (теор. 105,
стр. 219). Будем искать параметризацию в следующем виде:
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умноже-
нием:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
1
2
−1
1
=
1
−1
4
−2
для первого координатного полинома и, аналогично, для второго:
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
1
1
1
−1
=
1
1
−1
0
.
Таким образом, интересующая нас параметризация найдена:
p(u)=
1 −u +4u
2
− 2u
3
1+u −u
2
.
Выполним проверку. Должно выполняться четыре условия: два условия прохож-
дения кривой через ансамбль, и два условия направления прохождения.
p(0) =
1
1
= A
1
,p(1) =
1 −1+4− 2
1+1− 1
=
2
1
= A
2
.
Что касается направлений прохождения, то эти направления определяются каса-
тельными векторами к кривой p(u): при u =0и при u =1. Вычислим производ-
ную p
(u):
p
(u)=
−1+8u − 6u
2
1 −2u
,
после чего найдем векторы, касательные к кривой p(u) в точках A
1
и A
2
:
p
(0) =
−1
1
= v
1
,p
(1) =
1+8− 6
1 −2
=
1
−1
= v
2
.
Все четыре условия выполнены. Задача решена верно.
