Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.


6.1. Точная интерполяция 141
значно, исходя из координат точек опорного ансамбля:
a
10
a
11
a
12
=
100
−34−1
2 −42
x
A
x
B
x
C
,
a
20
a
21
a
22
=
100
−34−1
2 −42
y
A
y
B
y
C
.
Матрица, фигурирующая в вычислениях, называется квадратичной матри-
цей точной интерполяции.
Доказательство Мы будем предполагать, что интересующая нас пара-
метризация является равномерной на отрезке [0, 1], то есть —
p(0) = A, p(1/2) = B, p(1) = C.
Придавая переменной u значение 0, приходим к следующему векторному
равенству:
a
10
+ a
11
· 0+a
12
· 0
2
a
20
+ a
21
· 0+a
22
· 0
2
=
x
A
y
A
, откуда
a
10
a
20
=
x
A
y
A
.
Далее, придавая переменной u значение 1/2, получим:
a
10
+ a
11
· 1/2+a
12
· (1/2)
2
a
20
+ a
21
· 1/2+a
22
· (1/2)
2
=
x
B
y
B
, откуда
a
10
+ a
11
· 1/2+a
12
· 1/4
a
20
+ a
21
· 1/2+a
22
· 1/4
=
x
B
y
B
.
Наконец, придавая переменной u значение 1, получим еще одно векторное
равенство:
a
10
+ a
11
· 1+a
12
· 1
2
a
20
+ a
21
· 1+a
22
· 1
2
=
x
C
y
C
, откуда
a
10
+ a
11
+ a
12
a
20
+ a
21
+ a
22
=
x
C
y
C
.
Рассмотрим равенства первых координат в полученных трех векторных ра-
венствах. Они образуют линейную систему относительно переменных a
10
,
a
11
, a
12
, состоящую из трех уравнений:
a
10
= x
A
,
a
10
+
1
2
a
11
+
1
4
a
12
= x
B
,
a
10
+ a
11
+ a
12
= x
C
.
Воспользуемся для ее решения методом матричного обращения, для чего
преобразуем ее предварительно к матричному виду:
100
11/21/4
111
a
10
a
11
a
12
=
x
A
x
B
x
C
.
142 Глава 6. Интерполяция кривых
Отсюда неизвестные a
10
, a
11
, a
12
выражаются в виде вектора-столбца:
a
10
a
11
a
12
=
100
11/21/4
111
−1
x
A
x
B
x
C
.
Остается вычислить обратную матрицу. Для ее нахождения воспользуемся
методом Гаусса.
100
11/21/4
111
100
010
001
−I
−I
∼
100
01/21/4
011
100
−110
−101
4
∼
∼
100
021
011
100
−440
−101
−III
∼
100
010
011
10 0
−34−1
−10 1
−II
∼
∼
100
010
001
100
−34−1
2 −42
−II
Таким образом, выражение для вычисления коэффициентов первого пара-
метризующего многочлена получено:
a
10
a
11
a
12
=
100
−34−1
2 −42
x
A
x
B
x
C
.
Коэффициенты второго многочлена параметризации вычисляются анало-
гично.
Теорема доказана
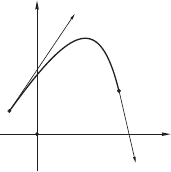
Пример 92 Провести точную интерполяцию опорного ансамбля, состоящего из
трех точек A(−1, 1), B(2, 2), C(1, 0).
Будем искать интерполирующую кривую p(u) в виде квадратичной параметриза-
ции:
p(u)=
a
10
+ a
11
u + a
12
u
2
a
20
+ a
21
u + a
22
u
2
.
Для нахождения коэффициентов параметризующих многочленов воспользуемся
теоремой о точной интерполяции (см. теор. 104, стр. 218). Для первого интерпо-
лирующего многочлена:
a
10
a
11
a
12
=
100
−34−1
2 −42
−1
2
1
=
−1
10
−8
.
И аналогично вычисляются коэффициенты второго интерполирующего многочле-
на:
a
20
a
21
a
22
=
100
−34−1
2 −42
1
2
0
=
1
5
−6
.
Следовательно, интересующая нас параметризация имеет следующий вид:
6.2. Интерполяция в форме Эрмита 143
p(u)=
−1+10u − 8u
2
1+5u − 6u
2
.
Аналогичные (хотя и более громоздкие) рассуждения позволяют доказать
аналогичную теорему для опорного ансамбля из четырех точек.
Теорема 82 (точная кубическая интерполяция) Для любого опорно-
го ансамбля, состоящего из четырех точек A(x
A
,y
A
), B(x
B
,y
B
), C(x
C
,y
C
),
D(x
D
,y
D
), существует единственная точно интерполирующая его кривая,
являющаяся кубической параметризацией вида:
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
причем коэффициенты параметризующих многочленов вычисляются одно-
значно, исходя из координат точек опроного ансамбля:
a
10
a
11
a
12
a
13
=
1000
−5.594.51
9 −22.518−4.5
−4.513.5 −13.54.5
x
A
x
B
x
C
x
D
,
a
20
a
21
a
22
a
23
=
1000
−5.594.51
9 −22.518−4.5
−4.513.5 −13.54.5
y
A
y
B
y
C
y
D
.
Матрица, фигурирующая в вычислениях называется матрицей точной ку-
бической интерполяции.
6.2 Интерполяция в форме Эрмита
При увеличении точек, участвующих в интерполя-
A
B
w
v
x
y
0
Рис. 6.2: Интерполя-
ция в форме Эрмита
ции, алгоритмы точной интерполяции становятся
неэффиктивными. Действительно, при этом воз-
растает степень интерполирующих многочленов и,
следовательно, вычислительная сложноть.
Выходом из этой, тупиковой, на первый взгляд,
ситуации состоит в разбиении опорного ансамбля,
содержащего большое число точек, на отдельные
группы: пары, тройки и т д.
При этом последняя точка предыдущей группы
служит первой точкой последующей, что выводит на первый план вопросы
корректного совмещения соседних сегментов. В большинстве случаев тре-
буется, чтобы в точках сопряжения кривая не теряла гладкости.
Оказывается, что если на точки ансамбля наложить дополнительные усло-
вия (указать еще направление прохождения кривой через каждую точку
ансамбля), то задача может быть решена при помощи интерполирущих
многочленов степени не выше третьей, и это позволяет сделать алгороитм
Эрмита.
144 Глава 6. Интерполяция кривых
Алгоритм Эрмита интерполяции плоских кривых служит теоретическим
обоснованием более распространенного на практике алгоритма Безье. Мы
уделим эрмитовой интерполяции гораздо большее внимание, нежели кри-
вым Безье именно по этой причине — Безье лишь приложил технику Эр-
мита к прикладным вопросам.
Определение 63 (эрмитова интерполирующая кривая) Пусть на
плоскости π фиксированы две точки A(x
A
,y
A
) и B(x
B
,y
B
). Интерполиру-
ющей кривой в форме Эрмита для опорного ансамбля, состоящего из этих
точек, называется кривая, стартующая в точке A в направлении данного
вектора v =(x
v
,y
v
) и финиширующая в точке B в направлении еще одного
данного вектора w =(x
w
,y
w
).
Итак, эримитова интерполяция харатеризуется четырьмя данными объек-
тами: двумя точками опорного ансамбля и двумя векторами, указывающи-
ми на направления старта и финиша (см. рис. 6.2, стр. 143). Наша бли-
жайшая цель — научиться аналитически описывать такие кривые в виде
полиномиальных параметризаций.
Теорема 83 (интерполяция в форме Эрмита) Пусть кривая p(u) стар-
тует в точке A(x
A
,x
B
) в направлении вектора v =(x
v
,y
v
) и финиширует
в точке B(x
B
,y
B
) в направлении вектора w =(x
w
,y
w
). Тогда существует
единственная кубическая параметризация этой кривой
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
причем коэффициенты параметризующих многочленов вычисляются по сле-
дующим формулам:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
x
A
x
B
x
v
x
w
,
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
y
A
y
B
y
v
y
w
.
Матрица, фигурирующая в вычислениях, называется матрицей Эрмита.
Доказательство Доказательство этой теоремы во многом аналогично до-
казательству теоремы о точной квадратичной интерполяции (см. теор. 104,
ср. 218)
Мы будем предполагать, что интересующая нас параметризация является
равномерной на отрезке [0, 1]. Это означает, что
p(0) = A, p(1) = B.
Придавая переменной u значение 0, получим следующее векторное равен-
6.2. Интерполяция в форме Эрмита 145
ство:
a
10
+ a
11
· 0+a
12
· 0
2
+ a
13
· 0
3
a
20
+ a
21
· 0+a
22
· 0
2
+ a
23
· 0
3
=
x
A
y
A
, откуда
a
10
a
20
=
x
A
y
A
.
Далее, придавая переменной u значение 1, получим еще одно векторное
равенство:
a
10
+ a
11
· 1+a
12
· 1
2
+ a
13
· 1
3
a
20
+ a
21
· 1+a
22
· 1
2
+ a
23
· 1
3
=
x
B
y
B
, откуда
a
10
+ a
11
+ a
12
+ a
13
a
20
+ a
21
+ a
22
+ a
23
=
x
B
y
B
.
Тем самым, на коэффициенты параметризующих многочленов мы нало-
жили два условия: условия прохождения кривой через точки опорного ан-
самбля. Имеются еще два условия: условия направлений старта и финиша.
Рассмотрим эти условия с аналитической точки зрения. Они означают, что
нам даны касательные векторы к кривой: в точке A — это вектор v,ав
точке B — вектор w. Воспользуемся теоремой о геометрическом смысле
производной функции, заданной параметрически (см. теор. 78, стр. 135).
Согласно этой теореме, имеем:
p
(0) = v, p
(1) = w.
Вычислим производную функции p(u) (это делается элементарно, так как
ее координатными функциями служат многочлены):
p
(u)=
a
11
+2a
12
u +3a
13
u
2
a
21
+2a
22
u +3a
23
u
2
.
Теперь мы можем получить еще два векторных равенства. Придавая пере-
менной u значение 0, получим:
a
11
+2a
12
· 0+3a
13
· 0
2
a
21
+2a
22
· 0+3a
23
· 0
2
=
x
v
y
v
, откуда
a
11
a
21
=
x
v
y
v
.
Наконец, придавая переменной u значение 1, получим еще одно векторное
равенство:
a
11
+2a
12
· 1+3a
13
· 1
2
a
21
+2a
22
· 1+3a
23
· 1
2
=
x
w
y
w
, откуда
a
11
+2a
12
+3a
13
a
21
+2a
22
+3a
23
=
x
w
y
w
.
Рассмотрим равенства первых координат в полученных четырех векторных
равенствах. Они образуют линейную систему относительно переменных a
10
,
a
11
, a
12
, a
14
, состоящую из четырех уравнений:
a
10
= x
A
,
a
10
+ a
11
+ a
12
+ a
13
= x
B
,
a
11
= x
v
,
a
11
+2a
12
+3a
13
= x
w
.
146 Глава 6. Интерполяция кривых
Воспользуемся для ее решения методом матричного обращения, для чего
преобразуем ее предварительно к матричному виду:
1000
1111
0100
0123
a
10
a
11
a
12
a
13
=
x
A
x
B
x
v
x
w
.
Отсюда неизвестные a
10
, a
11
, a
12
и a
13
выражаются в виде вектора-столбца:
a
10
a
11
a
12
a
14
=
1000
1111
0100
0123
−1
x
A
x
B
x
v
x
w
.
Остается вычислить обратную матрицу. Для ее нахождения можно вос-
пользоваться, например, методом Гаусса (выкладки мы опускаем, в виду
их тривиальности). Тем самым, получается формула для вычисления коэф-
фициентов первого многочлена параметризации интерполирующей кривой
в форме Эрмита:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
x
A
x
B
x
v
x
w
.
Коэффициенты второго многочлена параметризации вычисляются анало-
гично.
Теорема доказана
Пример 93 Пусть кривая p(u) проходит через точки A(1, 2) и B(2, 1) в направ-
лении векторов v =(1, 1) и w =(−1, −1). Требуется описать кривую p(u) пара-
метрически.
Задача решается при помощи только что доказанной теоремы об эрмитовой ин-
терполяции (см. теор. 83, стр. 144). Будем искать параметризацию в следующем
виде:
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умноже-
нием:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
1
2
1
−1
=
1
1
2
−2
— для первого координатного полинома, и аналогично, для второго:
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
2
1
1
−1
=
2
1
−4
2
.
Таким образом, интересующая нас параметризация найдена:
p(u)=
1+u +2u
2
− 2u
3
2+u −4u
2
+2u
3
.
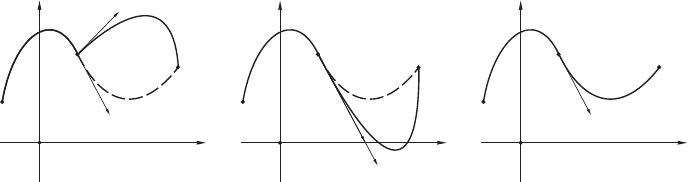
6.2. Интерполяция в форме Эрмита 147
x
y
0
A
B
C
u
v
(a) Сопряжение не являет-
ся гладким.
x
y
0
B
C
A
u
v
(b) Сопряжение является
геометрически гладким.
x
y
0
B
C
A
u = v
(c) Сопряжение является
параметрически гладким.
Рис. 6.3: Гладкость сопряжения сегментов.
Определение 64 (гладкость сопряжения сегментов) Допустим, неко-
торая кривая p(u) проходит через три точки опорного ансамлбя: A, B и C.
С точки зрения эрмитовой интерполяции, мы можем рассматривать ее как
состоящую из двух сегментов: AB и BC.
1. Если вектор финиша сегмента AB не параллелен вектору старта сег-
мента BC, то сопряжение сегментов не является гладким.
2. Если вектор финиша сегмента AB сонаправлен вектору старта сегмен-
та BC, то сопряжение сегментов называется геометрически гладким.
3. Если же вектор финиша сегмента AB в точности равен вектору старта
сегмента BC, то сопряжение сегментов параметрически гладкое.
Отметим, что, с точки зрения точной интерполяции, вопрос о гладкости со-
пряжения сегментов вообще не встает: она подразумевается как данность.
Но если опорный ансамбль состоит из достаточно большого числа точек, то
точная интерполяция приводит к огромному числу вычислений. Эрмитов
же алгоритм позволяет рассматривать двухточечные ансамбли как отдель-
ные сегменты и сопрягать их с любой гладкостью при помощи одних и тех
же действий.
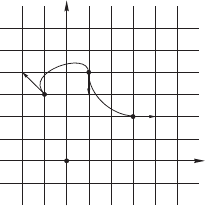
Пример 94 Пусть требуется провести кривую через три точки данного опорно-
го ансамбля A(1, 1), B(3, 1), C(5, 1) так, чтобы кривая стартовала в точке A в
направлении вектора v =(0, 1), проходила через точку B в направлении вектора
w =(0, −1) и финишировала в точке C в направлении вектора s =(1, 0). Факти-
чески, нам придется решить дважды задачу об эрмитовой интерполяции ансабля
из двух точек:
1. для точек A(1, 1) и B(3, 1) с направлениями v =(0, 1) и w =(0, −1),
2. для точек B(3, 1) и C(5, 1) с направлениями w =(0, −1) и s =(1, 0).
Приступим к решению первой задачи. Будем искать эрмитову интерполяционную
кривую p(u) в виде кубической параметризации:
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умноже-
нием:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
1
3
0
0
=
1
0
6
0
148 Глава 6. Интерполяция кривых
— для первого координатного полинома и, аналогично, для второго:
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
1
1
1
−1
=
1
1
−1
0
.
Таким образом, интересующая нас параметризация найдена:
p(u)=
1+6u
2
− 4u
3
1+u −u
2
.
Теперь — параметризуем кривую на втором сегменте за счет функции q(u).Будем
искать эрмитову интерполяционную кривую q(u) в виде кубической параметри-
зации:
q(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умноже-
нием:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
3
5
0
1
=
3
0
5
−3
— для первого координатного полинома и, аналогично, для второго:
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
1
1
−1
0
=
1
−1
2
−1
.
Таким образом, интересующая нас параметризация найдена:
q(u)=
3+5u
2
− 3u
3
1 −u +2u
2
− u
3
.
Итак, окончательно кривая параметризуется на интервале [0, 1] двумя эрмитовы-
ми интерполяциями p(u) и q(u):
p(u)=
1+6u
2
− 4u
3
1+u −u
2
,q(u)=
3+5u
2
− 3u
3
1 −u +2u
2
− u
3
.
6.2.1 Кривые Безье
Определение 65 (кривые Безье) Рассмотрим ансамбль из четырех опор-
ных точек A, B, C, D. Зададимся условием, что стартовая и финишная
точки формируемой кривой должны совпадать соответственно с A и D.
Две другие опорные точки B и C используются не для интерполяции, а
для задания направлений касания в конечных точках в виде двух векто-
ров: в точке A это вектор 3 · AB, а в точке D — вектор 3 · CD. Кривая,
удовлетворяющая перечисленным условиям называется кривой Безье.
Мы видим, что фактически кривые Безье — это одна из вариаций на те-
му интерполирующих кривых в форме Эрмита (разница лишь в способе
задания касательных векторов). Так же, как и в случае эрмитовой интер-
поляции, справедлива аналогичная теорема:
6.3. Пример алгоритма интерполяции 149
Теорема 84 (интерполяция в форме Безье) Пусть кривая p(u) стар-
тует в точке A(x
A
,x
B
) и финиширует в точке D(x
D
,y
D
), причем направ-
ление старта задано вектором AB =(x
AB
,y
AB
), а направление финиша
— вектором CD =(x
CD
,y
CD
). Тогда существует единственная кубическая
параметризация этой кривой
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
причем коэффициенты параметризующих многочленов вычисляются по сле-
дующим формулам:
a
10
a
11
a
12
a
13
=
1000
−3300
3 −630
−13−31
x
A
x
D
x
AB
x
CD
,
a
20
a
21
a
22
a
23
=
1000
−3300
3 −630
−13−31
y
A
y
D
y
AB
y
CD
.
Матрица, фигурирующая в вычислениях, называется матрицей Безье.
6.3 Пример алгоритма интерполяции
Постановка задачи
Точка M стартует в пункте A(−1, 3) в направлении вектора a(−1, 1) со
скоростью v
a
=5, проходит через точку B(1, 4) в направлении вектора
b =(0, −1) со скоростью v
b
=5и финиширует в точке C(3, 2) в направле-
нии вектора c =(1, 0) со скоростью v
c
=3.
Тебуется изобразить траекторию точки M .
6.3.1 Геометрическая версия алгоритма
С наглядно-геометрической точки зрения за-
A
B
C
a
b
c
x
y
0
Рис. 6.4: Кривая ABC.
дача решается лишь приблизительно. А имен-
но: мы можем точно изобразить на плоскости
опорные точки и точно же изобразить векто-
ры направлений: стартовый, промежуточный
и финишный. Вся остальная доступная нам де-
ятельность — это ручное проведение прибли-
зительно так ведущей себя кривой (заметим,
кстати, что таких кривых мы можем нарисо-
вать несколько, так как характер их поведения
известен нам лишь в узловых точках).
Эрмитов же алгоритм интерполяции позволит провести точное построение
кривой, удовлетворяющей данным требованиям, причем такая кривая ока-
жется единственной.

150 Глава 6. Интерполяция кривых
6.3.2 Аналитическая версия алгоритма
Будем искать параметризацию формируемой кривой в виде эрмитовой ин-
терполяции. С этой точки зрения кривая состоит из двух сегментов: AB
и BC, причем гладкость их сопряжения является параметрической (см.
опр. 89, стр. 221).
Для решения задачи нам необходимо знать векторы, касательные к сегмен-
там кривой. Вычислим их. В точках A, B и C это соответственно:
v
a
|a|
· a =
5
(−1)
2
+1
2
· (−1, 1) = (−3. 536, 3. 536) ,
v
b
|b|
· b =
5
0
2
+(−1)
2
· (0, −1) = (0, −5) ,
v
c
|c|
· c =
3
√
1
2
+0
2
· (1, 0) = (3, 0) .
Теперь мы можем описать сегменты кривых как две равномерные на от-
резке [0, 1] кубические параметризации p(u) и q(u). На сегменте AB это
функция p(u):
p(u)=
a
10
+ a
11
u + a
12
u
2
+ a
13
u
3
a
20
+ a
21
u + a
22
u
2
+ a
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умно-
жением:
a
10
a
11
a
12
a
13
=
1000
0010
−33−2 −1
2 −211
−1
1
−3. 536
0
=
1
−3. 536
13. 072
−7. 536
— для первого координатного полинома и, аналогично, для второго:
a
20
a
21
a
22
a
23
=
1000
0010
−33−2 −1
2 −211
3
4
3. 536
−5
=
3
3. 536
0. 929
−3. 464
.
Таким образом, интересующая нас параметризация найдена:
p(u)=
−1 − 3. 536 · u +13. 072 · u
2
− 7. 536 · u
3
3+3. 536 · u − 0. 928 · u
2
− 3. 464 · u
3
.
Аналогично поступаем на сегменте BC, формируя параметризацию q(u):
q(u)=
b
10
+ b
11
u + b
12
u
2
+ b
13
u
3
b
20
+ b
21
u + b
22
u
2
+ b
23
u
3
,
где коэффициенты координатных полиномов вычисляются матричным умно-
жением:
b
10
b
11
b
12
b
13
=
1000
0010
−33−2 −1
2 −211
1
3
0
3
=
1
0
3
−1
