Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

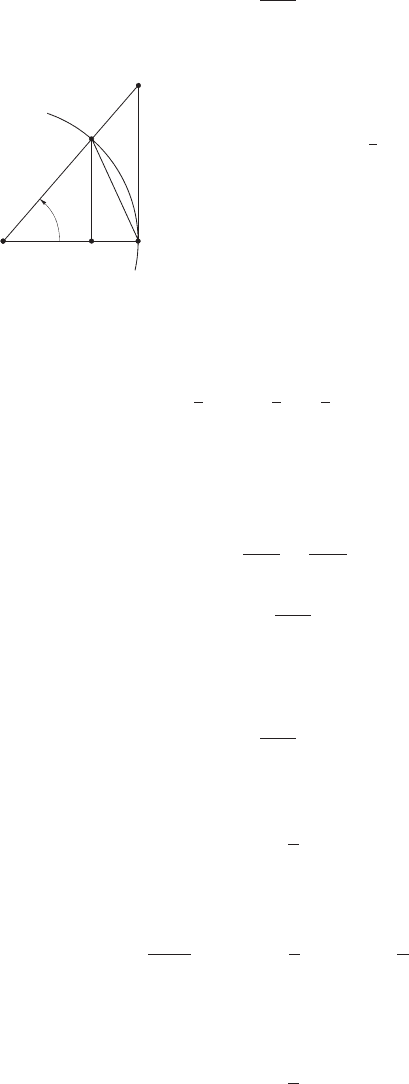
5.1. Пределы. Непрерывность функций 111
Пример 70 (первый замечательный предел) Покажем, что предел отноше-
ния синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен
единице:
lim
x→0
sin x
x
=1.
Заметим, что так как x стремится к нулю, можно
A
B
C
D
x
0
Рис. 5.1: Первый замеча-
тельный предел.
считать, что 0 <x<π/2.
В тригонометрическом круге единичного радиуса
построим угол x =
AOB.
Пусть DB — длина перпендикуляра, опущенного
из точки B на радиус OA, и пусть AC — отрезок
касательной, проведенной к окружности в точке
A до пересечения ее с продолжением радиуса AB.
Очевидно, что площадь треугольника OAB мень-
ше площади сектора OAB, которая, в свою оче-
редь, меньше площади треугольника OAC.Так
как DB =sinx и AC =tgx, то, на основании
формул элементарной геометрии, получим:
1
2
sin x<
1
2
x<
1
2
tg x,
или, умножая это двойное неравенство на 2:
sin x<x<tg x.
Разделим все части полученного двойного неравенства на положительную вели-
чину sin x:
1 <
x
sin x
<
1
cos x
.
Производя алгебраическое обращение этого двойного неравенства, получим:
cos x<
sin x
x
< 1 .
Очевидно, что при x, стремящемся к нулю, cos x стремится к 1. Поэтому функция
sin x/x заключена между функциями, имеющими общий предел, равный единице.
Отсюда, на основании теоремы о промежуточной функции (см. теор. 49, стр. 110),
заключаем:
lim
x→0
sin x
x
=1.
Пример 71 (второй замечательный предел) Покажем, что
lim
x→∞
1+
1
x
x
= e.
Введем натуральный аргумент n =[x], где квадратные скобки означают целую
часть числа. Тогда
1+
1
n +1
n
<
1+
1
x
x
<
1+
1
n
n+1
,
причем последовательности в левой и в правой частях этого двойного неравен-
ства имеют одинаковый предел e (см. пример 67, стр. 107). Отсюда, на основании
теоремы о пределе промежуточной функции (см. теор. 49, стр. 110), заключаем:
lim
x→∞
1+
1
x
x
= e.

112 Глава 5. Математический анализ
Определение 48 (бесконечно малые функции, порядок малости)
Прежде всего отметим, что, по аналогии с бесконечно малыми последова-
тельностями (см. опр. 43, стр. 99), функция α(x) называется бесконечно
малой в окрестности точки a, если ее предел в этой точке равен нулю.
Пусть α(x) и β(x) — две бесконечно малые функции. Тогда
1. Они называются бесконечно малыми одного порядка, если предел их
отношения конечен и отличен от нуля:
lim
x→a
α(x)
β(x)
= c =0.
2. Они называются эквивалентными, если предел их отношения равен
единице:
lim
x→a
α(x)
β(x)
=1.
Эквивалентность бесконечно малых обозначается следующим обра-
зом: α ∼ β.
3. Наконец, бесконечно малая функция α(x) называется бесконечно ма-
лой более высокого порядка, нежели бесконечно малая функция β(x),
если
lim
x→a
α(x)
β(x)
=0.
Этот факт обозначается следующим образом: α(x)=o(β(x)).
Пример 72 Функции sin x и x являются эквивалентными бесконечно малыми в
окрестности нуля (см. опр. 48, стр. 112 и пример 70, стр. 111).
Пример 73 Функция x
2
в окрестности нуля имеет больший порядок малости,
нежели функция x,таккак:
lim
x→0
x
2
x
= lim
x→0
x =0.
Отсюда, на основании определения порядка малости (см. опр. 48, стр. 112), за-
ключаем: x
2
= o(x) в окрестности нуля
6
.
Теорема 50 (асимптотические формулы) В окрестности нуля справед-
ливы следующие формулы:
1. sin x = x + o(x),
2. cos x =1− x
2
/2+o(x
2
),
6
Соотношение α(x)=o(β(x)) обладает рядом специфичных свойств. Его нельзя вос-
принимать, как обычное равенство. Фактически оно означает, что функция α(x) при-
надлежит к классу функций более высокого порядка малости, нежели функция β(x).
Поэтому, например, равенство x
2
= o(x) является верным, а запись вида o(x)=x
2
не
верна, так как нельзя утверждать, что весь класс функций более высокого порядка ма-
лости, нежели x исчерпывается единственной функцией x
2
. Принимая это во внимание,
можно понять, почему, например, o(x
2
+ x)=o(x
2
) или o(3x)=o(x) и т. д. — речь идет
о классах функций, а не о точных равенствах.

5.1. Пределы. Непрерывность функций 113
3. log
a
(x +1)=x/ ln a + o(x), в частности — ln(x +1)=x + o(x),
4. a
x
=1+x ln a + o(x), в частности — e
x
=1+x + o(x).
Доказательство Докажем первую из этих формул (остальные примем
без доказательства). Мы можем воспользоваться первым замечательным
пределом (см. пример 70, стр. 111):
lim
x→0
sin x
x
=1.
Вычитая из обеих частей единицу, получим:
lim
x→0
sin x
x
− 1 = lim
x→0
sin x
x
− 1
= lim
x→0
sin x − x
x
=0.
Согласно определению порядка малости (см. опр. 48, стр. 112), это в точ-
ности означает, что sin x − x = o(x).Отсюдаsin x = x + o(x).
Теорема доказана.
Пример 74 Вычислим следующий предел:
lim
x→0
cos x − cos 3x
x
2
= lim
x→0
1 −x
2
/2+o(x
2
) −(1 − 9x
2
/2+o(9x
2
))
x
2
=
= lim
x→0
4x
2
+ o(x
2
)
x
2
= lim
x→0
4x
2
x
2
+ lim
x→0
o(x
2
)
x
2
=4.
Прокомментируем выкладку. На первом шаге мы применили асимптотические
формулы к функциям cos x и cos 3x (см. теор. 50, стр. 112). Далее — выполнили
элементарные преобразования в числителе, учитывая, что символы o(x
2
) и o(9x
2
)
означают не слагаемые, а классы функций. Наконец, на последнем шаге мы вос-
пользовались теоремой о пределе суммы (см. теор. 48, стр. 109) и преобразовали ее
к сумме пределов, после чего — воспользовались определением бесконечно малой
более высокого порядка (см. опр. 48, стр. 112).
5.1.6 Непрерывность
x
y
0
y = f(x)
x
0
(a) Функция непрерывна в точ-
ке x
0
.
x
y
0
y = f(x)
x
0
(b) Функция терпит разрыв.
Рис. 5.2: Интуитивное представление непрерывности.
114 Глава 5. Математический анализ
Понятие непрерывности является ключевым понятием математическо-
го анализа. Несмотря на то, что интуитивно оно совершенно очевидно (см.
рис. 5.2, стр. 113), его корректное математическое определение весьма слож-
но. Лишь теперь, после достаточно подробного изложения теории пределов,
мы можем его дать.
Определение 49 (непрерывность функции в точке) Функция f(x)
называется непрерывной в точке x
0
, если
1. она определена в точке x
0
,
2. существует предел функции f(x) в точке x
0
, причем он равен ее зна-
чению в этой точке:
lim
x→x
0
f(x)=f(x
0
) .
Теорема 51 (геометрический смысл непрерывности) Функция f(x)
является непрерывной в точке x
0
, если бесконечно малому приращению ее
аргумента в этой точке отвечает бесконечно малое приращение функции:
lim
∆x→0
∆f =0,
где приращение аргумента ∆x = x − x
0
, а приращение функции ∆f =
f(x
0
+∆x) − f(x
0
).
Доказательство Данное утверждение является утверждением эквива-
лентности, то есть — требует доказательства в обе стороны. Пусть сначала
lim
∆x→0
∆f =0.
Тогда, пользуясь теоремой о пределе суммы (см. теор. 48, стр. 109), а также
тем, что x стремится к x
0
при стремлении ∆x к нулю, получим:
lim
∆x→0
f(x
0
+∆x) − lim
∆x→0
f(x
0
)=0, откуда lim
x→x
0
f(x)=f(x
0
) .
Таким образом, утверждение доказано нами в одну сторону. Докажем те-
перь обратное утверждение. Пусть
lim
x→x
0
f(x)=f(x
0
) .
Обозначим x − x
0
=∆x.Тогдаx = x
0
+∆x, и мы можем записать:
lim
∆x→0
f(x
0
+∆x)=f(x
0
) .
Перенесем правую часть налево и воспользуемся тем, что предел константы
равен ей самой:
lim
∆x→0
f(x
0
+∆x) − f(x
0
)=0, откуда lim
∆x→0
(f(x
0
+∆x) − f(x
0
)) = 0 ,
Пользуясь формулой для приращения функции, окончательно получим:
lim
∆x→0
∆f =0.

5.1. Пределы. Непрерывность функций 115
Теорема доказана.
Таким образом, имеется два эквивалентных определения непрерывности
функции в точке: собственно в смысле определения (см. опр. 49, стр. 114)
и в смысле доказанной только что теоремы (см. теор. 51, стр. 114). В зави-
симости от ситуации, мы будем пользоваться тем или иным определением.
Понятие непрерывности в точке непосредственно обобщается на произволь-
ные множества точек числовой прямой.
Определение 50 (непрерывность на множестве) Функция f(x) назы-
вается непрерывной на некотором множестве X (в качестве которого могут
выступать открытые и замкнутые интервалы как конечные, так и беско-
нечные), если она непрерывна в любой точке этого множества.
Далее нас будут интерсовать условия, при которых функции являются непре-
рывными.
Теорема 52 (о суперпозиции непрерывных функций) Суперпозиция
непрерывных функций является непрерывной функцией.
Доказательство Пусть имеется сложная функция y = g(f (x)). Пусть функ-
ция f (x) непрерывна в точке x
0
, а функция g(f) непрерывна в точке f
0
=
f(x
0
). Придадим переменной x бесконечно малое приращение ∆x в точке
x
0
. Тогда, в силу непрерывности функции f(x), она получит бесконечно ма-
лое приращение ∆f (см. теор. 51, стр. 114). В силу тех же причин, функция
g(f) при бесконечно малом приращении аргумента ∆f получит бесконечно
малое приращение ∆g.
Итак, мы показали, что бесконечно малому приращению переменной x от-
вечает бесконечно малое приращение функции g. В силу теоремы о геомет-
рическом смысле непрерывности (см. теор. 51, стр. 114), это означает, что
функция g является непрерывной функцией переменной x.
Теорема 53 (о неперерывности элементарных функций) Основные
элементарные функции
7
являются непрерывными.
Доказательство Нам нужно доказать, что функции y = x
n
, y =sinx,
y =cosx и y = a
x
являются непрерывными.
1. Случай степенной функции y = x
n
является тавтологичным. Действи-
тельно в силу свойств пределов (см. теор. 48, стр. 109), имеем:
lim
x→a
x
n
=
lim
x→a
x
n
= a
n
.
По определению (см. опр. 49, стр. 114) это означает непрерывность
степенной функции в любой точке.
7
Напомним, что основных элементарных функций не так много: к ним относятся сте-
пенные, тригонометрические и показательные функции. Все остальные элементарные
функции получаются при помощи алгебраических операций, суперпозиций и обращений
основных элементарных функций.
116 Глава 5. Математический анализ
2. Сложнее обстоит дело с тригонометрическими функциями. Обозна-
чим y = x − a, откуда x = y + a.Еслиx стремится к a, то при этом y
стремится к нулю. Поэтому:
lim
x→a
sin x = lim
y→0
sin(y + a) = lim
y→0
(sin y cos a +cosy sin a)=
=cosa lim
y→0
sin y +sina lim
y→0
cos y =
=cosa lim
y→0
(y + o(y)) + sin a lim
y→0
(1 − y
2
/2+o(y
2
)) =
=cosa · 0+sina · 1=sina.
Прокомментируем выкладку. Сначала мы по известным тригономет-
рическим формулам преобразовали синус суммы. Затем — восполь-
зовались свойствами пределов (см. теор 48, стр. 109) и вынесли по-
стоянные множители sin a и cos a из под знаков пределов. После чего
применили асимптотические формулы (см. теор. 50, стр. 112) к функ-
циям sin y и cos y и, наконец, вычислили оставшиеся пределы, пользу-
ясь определением бесконечно малых (см. опр. 48, стр. 112).
В результате, мы получили:
lim
x→a
sin x =sina,
что, по определению (см. опр. 49, стр. 114) означает непрерывность
функции sin x в любой точке a.
3. Непрерывность функции cos x доказывается аналогично (с ипользова-
нием формулы косинуса суммы).
4. Покажем непрерывность показательной функции a
x
. Обозначим y =
x −b, откуда x = y + b.Еслиx стремится к b, то при этом y стремится
к нулю. Поэтому:
lim
x→b
a
x
= lim
y→0
a
y+b
= a
b
lim
y→0
a
y
= a
b
lim
y→0
(1 + y ln a + o(y)) = a
b
.
Комментарии к выкладке будут излишними (они повторяют уже ска-
занное выше). Из полученного соотношения
lim
x→a
a
x
= a
b
заключаем: показательная функция a
x
является непрерывной для лю-
бого a (см. опр. 49, стр. 114).
Теорема доказана.
Определение 51 (класс C
0
) О множестве функций, непрерывных на мно-
жестве X, говорят, что они принадлежат классу непрерывности C
0
.

5.2. Производные 117
Определение 52 Доказанные выше теоремы о непрерывных функциях позво-
ляют утверждать, что, например, функция
y =
e
x
2
+x
− 2x
sin x
является непрерывной всюду, за исключением тех точек, в которых она не опре-
делена (то есть точек вида x
n
= πn,гдеn — любое целое число). Таким образом,
эта функция принадлежит классу C
0
на указанном множестве.
5.2 Производные
В этом разделе мы разовьем одну из основных математических техник —
технику дифференцирования, которая находит широчайшее применение в
науке и технике. Далее, при построении интерполирующих кривых в форме
Эрмита (см раздел 6.2, стр. 143), мы получим некоторые приложения этой
техники. Однако не стот думать, что возможности дифференцирования ими
исчерпываются.
Более подробно с вопросами дифференциального исчисления можно озна-
комиться по многим классическим учебникам математического анализа:
Г. М. Фихтенгольца [F], С. М. Никольского [N], Н. С. Пискунова [P] и т. д.,
а так же по учебникам высшей математики для втузов: Кудрявцева и Де-
мидовича [KD], Шипачева [Sh] и других.
Практические задачи, относящиеся к данному разделу, представлены в при-
ложениях (см. приложение C.1, стр. 205).
5.2.1 Производная
В данном разделе мы вводим ключевое понятие математического анализа
— понятие производной функции в точке (см. опр. 53, стр. 117) и на множе-
стве (см. опр. 54, стр. 118). Кроме того, мы получим обобщающее понятие
непрерывности и очень важное для дальнейших целей
8
понятие гладкости
функции (см. опр. 56, стр. 119).
Определение 53 (производная функции в точке) Пусть функция f (x)
определена в некоторой окрестности точки x
0
.Пусть∆x — приращение
независимой переменной в этой точке, а ∆f — соответствующее ему прира-
щение функции. Тогда, если существует предел
lim
∆x→0
∆F
∆x
,
то он называется производной функции f(x) в точке x
0
.
Пример 75 Вычислим производную функции f(x)=x
2
в точке x
0
=3. Прида-
дим независимой переменной x бесконечно малое приращение ∆x. Тогда функция
f(x)=x
2
получит приращение
∆f = f (3 + ∆x) − f(3) = (3 + ∆x)
2
− 3
2
=9+6∆x +∆
2
x −9=6∆x +∆
2
x.
8
Речь идет о гладкости сопряжения сегментов кривой, сформированной по алгоритму
Эрмита (см. раздел 6.2, стр. 143).
118 Глава 5. Математический анализ
Пользуясь определением (см. опр. 53, стр. 117), составим выражение для произ-
водной функции в точке:
lim
∆x→0
∆f
∆x
= lim
∆x→0
6∆x +∆
2
x
∆x
= lim
∆x→0
6+
∆
2
x
∆x
= lim
∆x→0
(6 + ∆x)=
= lim
∆x→0
6 + lim
∆x→0
∆x =6.
Определение 54 (производная функции на множестве) Пусть X —
некоторое числовое множество, в качестве которого может выступать ин-
тервал числовой прямой (открытый или замкнутый, конечный или беско-
нечный), и пусть функция f(x) определена на X. Если в каждой точке
этого множества существует конечная производная функции f (x), то, со-
поставляя каждому значению переменной x
0
из X значение производной,
вычисленное в этой точке, получим новую функцию, которая называется
производной функции f(x) на множестве X. Она обозначается f
(x).
Пример 76 Вычислим производную функции f(x)=x
2
на всей числовой пря-
мой. Зафиксируем произвольно некоторое значение переменной x
0
и придадим
независимой переменной x бесконечно малое приращение ∆x в точке x
0
.Тогда
функция f(x)=x
2
получит приращение
∆f = f (x
0
+∆x)−f(x
0
)=(x
0
+∆x)
2
−x
2
0
= x
2
0
+2x
0
∆x+∆
2
x−x
2
0
=2x
0
∆x+∆
2
x.
Пользуясь определением (см. опр. 53, стр. 117), составим выражение для произ-
водной функции в точке:
lim
∆x→0
∆f
∆x
= lim
∆x→0
2x
0
∆x +∆
2
x
∆x
= lim
∆x→0
2x
0
+
∆
2
x
∆x
=
= lim
∆x→0
(2x
0
+∆x) = lim
∆x→0
2x
0
+ lim
∆x→0
∆x =2x
0
.
Таким образом, каждому значению переменной x
0
соответствует значение произ-
водной, вычисляемое в этой точке по формуле 2x
0
. Согласно определению (см.
пор. 54, стр. 118), это оначает, что
x
2
=2x.
Определение 55 (дифференцирование) Операция построения по дан-
ной функции ее производной называется дифференцированием.
Далее нас будут интересовать условия, при выполнении которых можно
дифференцировать функции.
Теорема 54 (необходимое условие дифференцируемости) Пусть
функция f (x) обладает производной в точке x
0
. Тогда она непрервна в этой
точке.
Доказательство Придадим переменной x приращение ∆x в точке x
0
То-
гда функция f(x) получит в этой точке приращение ∆f . При этом имеет
место очевидное алгебраическое тождество:
∆f =
∆f
∆x
· ∆x.

5.2. Производные 119
Перейдем в этом равенстве к пределу при бесконечно убывающем прира-
щении ∆x:
lim
∆x→0
∆f = lim
∆x→0
∆f
∆x
· lim
∆x→0
∆x = f
· 0=0.
Следовательно, бесконечно малому приращению аргумента x в точке x
0
от-
вечает бесконечно малое приращение функции f в этой точке. Это означает
(см. теор. 51, стр. 114), что функция f(x) является непрерывной в точке x
0
.
Теорема доказана.
Как обычно, необходимый признак дифференцируемости удобнее рассмат-
ривать как раз наоборот: как достаточный признак недифференцируемо-
сти. Сформулируем это в виде следующего утверждения.
Теорема 55 (достаточное условие недифференцируемости) Если
функция f(x) разрывна в точке x
0
, то не существует производной функции
f в этой точке.
Доказательство Данное утверждение эквивалентно необходимому при-
знаку дифференцируемости (см. теор. 54, стр. 118).
Теорема доказана.
Итак, если функция разрывна, то она заведеомо недифференцируема. Нель-
зя, однако, утверждать обратное: если функция непрерывна, то она не
обязвтельно является дифференцируемой.
Пример 77 Например, функция y = |x| является непрерывной в любой точке,
в частности и в точке x
0
=0. Однако, как мы вскоре убедимся, эта функция не
обладает производной в нуле. То есть — производная модуля как функция терпит
разрыввнуле.
Определение 56 (класс C
1
, гладкие функции) О множестве функций,
непрерывных на множестве X вместе со своими производными, говорят, что
они принадлежат классу непрерывности C
1
(их также называют гладкими
функциями).
Пример 78 Согласно данным выше определениям классов непрерывности C
0
и
C
1
(см. опр. 51 и 56, стр. 116, 119), можно утверждать, что функция y = x
2
является гладкой (см. пример 76, стр. 118). С другой стороны (см. пример 77,
стр. 119), |x|∈C
0
,но|x| /∈ C
1
. То есть — модуль является непрерывной функцией,
но не является гладкой.
5.2.2 Правила дифференцирования
Этот раздел принесет нам первые практические результаты в области диф-
ференцирования функций. Мы получим правила дифференцирования: пра-
вило дифференцирования суммы (см. теор. 56, стр. 119), правило диффе-
ренцирования произведения (см. теор. 57, стр. 120) и правило дифферен-
цирования частного (см. теор. 58, стр. 121).
Теорема 56 (о дифференцировании суммы) Пусть две данные функ-
ции f(x) и g(x) имеют производные в точке x
0
. Тогда их сумма также имеет
производную в точке x
0
, причем:
(f + g)
= f
+ g
.

120 Глава 5. Математический анализ
Доказательство Пусть y = f + g. Придадим переменной x бесконечно
малое приращение ∆x в точке x
0
. Тогда функция y получит приращение
∆y, причем:
y +∆y =(f +∆f)+(g +∆g)=(f + g)+(∆f +∆g) .
Отсюда ∆y =∆f +∆g. Для вычисления производной функции y в точке
x
0
воспользуемся определением (см. опр. 53, стр. 117):
y
=(f + g)
= lim
∆x→0
∆y
∆x
= lim
∆x→0
∆f +∆g
∆x
= lim
∆x→0
∆f
∆x
+ lim
∆x→0
∆g
∆x
= f
+ g
.
Теорема доказана.
Теорема 57 (о дифференцировании произведения) Пусть две функ-
ции f(x) и g(x) имеют производные в точке x
0
. Тогда их произведение также
имеет производную в точке x
0
, причем:
(fg)
= f
g + fg
.
Доказательство Пусть y = fg. Придадим переменной x бесконечно ма-
лое приращение ∆x в точке x
0
. Тогда функция y получит приращение ∆y,
причем:
y +∆y =(f +∆f)(g +∆g)=fg +∆fg + f∆g +∆f∆g.
Отсюда — ∆y =∆fg+f∆g +∆f∆g. Для вычисления производной функции
y в точке x
0
воспользуемся определением (см. опр. 53, стр. 117):
y
=(fg)
= lim
∆x→0
∆y
∆x
= lim
∆x→0
∆fg + f∆g +∆f ∆g
∆x
=
= lim
∆x→0
∆fg
∆x
+ lim
∆x→0
f∆g
∆x
+ lim
∆x→0
∆f∆g
∆x
=
= g lim
∆x→0
∆f
∆x
+ f lim
∆x→0
∆g
∆x
+ lim
∆x→0
∆f
∆x
lim
∆x→0
∆g =
= f
g + fg
+ f
· 0=f
g + fg
.
В течение выкладки мы пользовлись свойствами пределов (см. теор. 48,
стр. 109), разбивая предел суммы в сумму пределов и вынося постоянные
(не зависящие от приращения ∆x) множители.
Последнее звено выкладки нуждается в отдельном комментарии. Фигури-
рующий здесь предел приращения функции g обязан равняться нулю, так
как функция g по условию теоремы обладает производной в точке x
0
и,
следовательно (см. теор. 54, стр. 118), является непрерывной. Бесконечно
малому же приращению аргумента непрерывной функции отвечает беско-
нечно малое приращение функции (см. теор. 51, стр. 114).
Теорема доказана.
