Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.


5.1. Пределы. Непрерывность функций 101
Доказательство В силу опеределений бесконечно малой (см. опр. 43,
стр. 99) и ограниченной (см. опр. 42, стр. 97) последовательностей, суще-
ствует такое положительное M ,что
|f
n
| <M, для любого n ;
и для любого сколь угодно малого ε найдется номер N такой, что
|α
n
| <
ε
M
, для любого n>N.
Перемножая эти два неравенства, получим следующее: для любого сколь
угодно малого положительного ε найдется номер N такой, что
|f
n
· α
n
| = |f
n
|·|α
n
| <M·
ε
M
= ε.
По определению бесконечно малой последовательности (см. опр. 43, стр. 99)
это означает, что произведение {α
n
}·{f
n
} является бесконечно малой по-
следовательностью.
Теорема доказана.
Теорема 41 (об алгебраическом обращении) Пусть {A
n
} — бесконеч-
но большая последовательность. Тогда ее алгебраическое обращение 1/{A
n
}
— бесконечно малая последовательность.
Аналогично, если {α
n
} — бесконечно малая последовательность, то ее ал-
гебраическое обращение 1/{α
n
} — бесконечно большая последовательность.
Доказательство Докажем первое из утрверждений (второе доказывается
аналогично).
Воспользуемся определением бесконечно большой последовательности (см.
опр. 44, стр. 99): для любого, сколь угодно большого, положительного M,
найдется номер N такой, что
|A
n
| >M, для любого n>N.
Обращая это неравенство, получим:
1
|A
n
|
<
1
M
, для любого n>N.
Обозначим ε =1/M . Тогда полученное неравенство означает, что для лю-
бого сколь угодно малого положительного ε найдется номер N такой, что
1
|A
n
|
<ε, для любого n>N.
По определению бесконечно малой последовательности (см. опр. 43, стр. 99),
последовательность 1/{A
n
} является бесконечно малой.
Теорема доказана.
В заключение этого раздела отметим, что далеко не все действия с бесконеч-
но малыми и бесконечно большими последовательностями являются таким
102 Глава 5. Математический анализ
очевидными. Например, что произойдет, если мы попытаемся разделить
одну бесконечно малую последовательность на другую? Или перемножить
бесконечно малую и бесконечно большую последовательности?
Такие ситуации называются неопределенностями: вида [0/0] для отношения
двух бесконечно малых, [0 ·∞] для произведения бесконечно малой и бес-
конечно большой и т. д. Результатом раскрытия неопределенности может
оказаться как бесконечно малая, так и бесконечно большая или ограничен-
ная последовательности.
5.1.3 Свойства сходящихся последовательностей
В этом разделе мы получим ряд правил, позволяющих облегчить вычис-
ления пределов. Речь идет о вычислении пределов суммы (см. теор. 43,
cтр. 102), произведения (см. теор. 44, cтр. 103) и частного (см. теор. 45,
cтр. 104) сходящихся последовательностей. Начнем с того, что докажем сле-
дующее вспомогательное утверждение.
Теорема 42 (о представлении сходящейся последовательности)
Пусть последовательность {x
n
} сходится к пределу a:
lim
n→∞
x
n
= a.
Тогда последовательность {x
n
} может быть представлена в виде:
x
n
= a + α
n
,
где {α
n
} — бесконечно малая последовательность.
Доказательство Так как последовательность {x
n
} сходится к a, последо-
вательность {x
n
− a} также сходится, причем к нулю:
lim
n→∞
(x
n
− a)=0.
По определению бесконечно малой последовательности (см. опр. 43, стр. 99)
это означает, что последовательность {x
n
− a} является бесконечно малой:
x
n
− a = α
n
, отсюда x
n
= a − α
n
.
Теорема доказана.
Теорема 43 (о сумме сходящихся последовательностей) Пусть после-
довательности {x
n
} и {y
n
} являются сходящимися, причем
lim
n→∞
x
n
= a, lim
n→∞
y
n
= b.
Тогда их сумма также является сходящейся последовательностью, причем
lim
n→∞
(x
n
+ y
n
)=a + b.
5.1. Пределы. Непрерывность функций 103
Доказательство Последовательности {x
n
} и {y
n
} являются сходящими-
ся. Следовательно (см. теор. 42, стр. 102), они представимы в виде:
x
n
= a + α
n
,y
n
= b + β
n
,
где α
n
, β
n
— бесконечно малые последовательности. Складывая эти равен-
ства, получим:
x
n
+ y
n
= a + α
n
+ b + β
n
=(a + b)+(α
n
+ β
n
)=(a + b)+γ
n
,
где γ
n
= α
n
+ β
n
— бесконечно малая последовательность (см. теор. 38,
стр. 99). Итак, мы представили сумму последовательностей в виде:
x
n
+ y
n
=(a + b)+γ
n
,
где γ
n
— бесконечно малая последовательность. Согласно доказанному нами
выше утверждению о представлении сходящейся последовательности (см.
теор. 42, стр. 102), последовательность {x
n
+y
n
} является сходящейся, при-
чем:
lim
n→∞
(x
n
+ y
n
)=a + b.
Теорема доказана.
Теорема 44 (о произведении сходящихся последовательностей)
Пусть последовательности {x
n
} и {y
n
} являются сходящимися, причем их
пределы таковы:
lim
n→∞
x
n
= a, lim
n→∞
y
n
= b.
Тогда их произведение также является сходящейся последовательностью,
причем
lim
n→∞
(x
n
· y
n
)=a · b.
В частности, постоянный множитель можно выносить из-под знака предела:
lim
n→∞
( · x
n
)=c lim
n→∞
x
n
.
Доказательство Последовательности {x
n
} и {y
n
} являются сходящими-
ся. Следовательно (см. теор. 42, стр. 102), они представимы в виде:
x
n
= a + α
n
,y
n
= b + β
n
,
где α
n
, β
n
— бесконечно малые последовательности. Перемножая эти ра-
венства, получим:
x
n
· y
n
=(a + α
n
) ·(b + β
n
)=(a ·b)+(α
n
· b + β
n
· a + α
n
· β
n
)=(a ·b)+γ
n
,
где γ
n
= α
n
· b + β
n
· a + α
n
· β
n
. Покажем, что γ
n
— бесконечно малая
последовательность.
Действительно, первые два слагаемых — бесконечно малые, так как это про-
зведения бесконечно малых α
n
, β
n
и ограниченных последовательностей a,
b (см. тер. 40, стр. 100). Последнее слагаемое — также бесконечно малая, так
как это произведение двух бесконечно малых α
n
и β
n
(см. тер. 39, стр. 100).

104 Глава 5. Математический анализ
Следовательно, последовательность γ
n
является бесконечно малой как сум-
ма бесконечно малых последовательностей (см. тер. 38, стр. 99).
Итак, мы представили произведение последовательностей в виде:
x
n
· y
n
=(a · b)+γ
n
,
где γ
n
— бесконечно малая последовательность. Согласно доказанному нами
выше утверждению о представлении сходящейся последовательности (см.
теор. 42, стр. 102), последовательность {x
n
·y
n
} является сходящейся, при-
чем:
lim
n→∞
(x
n
· y
n
)=a · b.
Второе утверждение теоремы получается из только что доказанного, ес-
ли учесть, что, по определению предела последовательности (см. опр. 39,
стр. 96), предел постоянной равен ей самой.
Теорема доказана.
Теорема 45 (о частном сходящихся последовательностей) Пусть
две числовые последовательности {x
n
} и {y
n
} являются сходящимися, при-
чем
lim
n→∞
x
n
= a, lim
n→∞
y
n
= b.
Пусть, кроме того, b =0. Тогда их частное также является сходящейся
последовательностью, причем
lim
n→∞
x
n
y
n
=
a
b
.
Доказательство Последовательности {x
n
} и {y
n
} являются сходящими-
ся. Следовательно (см. теор. 42, стр. 102), они представимы в виде:
x
n
= a + α
n
,y
n
= b + β
n
,
где α
n
, β
n
— бесконечно малые последовательности. Разделим первое ра-
венство на второе и получим:
x
n
y
n
=
α
n
+ a
β
n
+ b
=
a
b + β
n
+
α
n
b + β
n
=
=
ab
b(b + β
n
)
+
α
n
b + β
n
=
ab + aβ
n
− aβ
n
b(b + β
n
)
+
α
n
b + β
n
=
=
a(b + β
n
)
b(b + β
n
)
+
α
n
b + β
n
−
aβ
n
b(b + β
n
)
=
a
b
+
1
b + β
n
α
n
−
a
b
β
n
=
a
b
+ γ
n
,
где γ
n
=
1
b + β
n
α
n
−
a
b
β
n
. Покажем, что γ
n
— бесконечно малая после-
довательность.
Действительно, второе слагаемое в скобках — это бесконечно малая по-
следовательность как произведение бесконечно малой β
n
и ограниченной
величины a/b (см. теор. 40, стр. 100). Далее, разность в скобках — это раз-
ность бесконечно малых, следовательно (см. теор. 38, стр. 99) это также
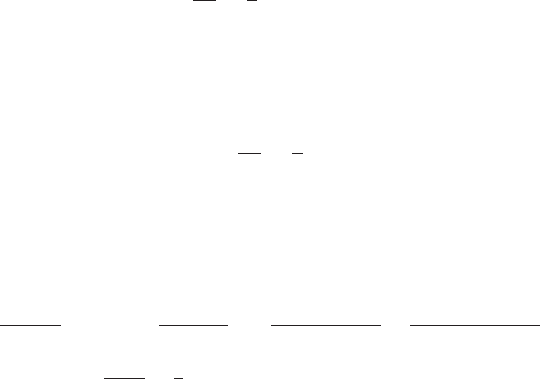
5.1. Пределы. Непрерывность функций 105
бесконечно малая последовательность. Наконец, коэффициент перед скоб-
кой — это ограниченная величина, так как ее знаменатель, очевидно, огра-
ничен (он является суммой ограниченной величины b и бесконечно малой
β
n
). Следовательно, последовательность γ
n
является бесконечно малой как
произведение бесконечно малой и ограниченной последовательностей (см.
теор. 40, стр. 100).
Итак, мы представили частное последовательностей в виде:
x
n
y
n
=
a
b
+ γ
n
,
где γ
n
— бесконечно малая последовательность. Согласно доказанному нами
выше утверждению о представлении сходящейся последовательности (см.
теор. 42, стр. 102), последовательность {x
n
/y
n
} является сходящейся, при-
чем:
lim
n→∞
x
n
y
n
=
a
b
.
Теорема доказана.
Пример 65 Вычислим следующий предел:
lim
n→∞
n
2
+ n
2n
2
+1
= lim
n→∞
1+1/n
2+1/n
2
=
lim(1 + 1/n)
lim(2 + 1/n
2
)
=
lim 1 + lim(1/n)
lim 2 + lim 1/n
2
=
=
1+0
2+0
=
1
2
.
Прокомментируем выкладку. На первом шаге мы просто выполнили тождествен-
ное преобразование подпредельного выражения. Затем — применили теорему о
пределе частного (см. теор. 45, стр. 104) и перешли к частному пределов. Далее
при помощи теоремы о пределе суммы (см. теор. 43, стр. 102), и в числителе, и в
знаменателе мы перешли к суммам пределов. После чего — воспользовались тем,
что предел постоянной равен ей самой, и, самое главное, тем, что алгебраическое
обращение бесконечно больших величин n и n
2
есть величины бесконечно малые.
5.1.4 Монотонные последовательности
В некоторых случаях мы не можем вычислить предел последовательно-
сти явно. Однако имеются приемы, одним из которых служит теорема о
монотонной ограниченной последовательности (см. теор. 46, стр. 106), поз-
воляющие утверждать, что предел все-таки существует. Более того, иногда
удается получить численное значение предела с любой точностью, как, на-
пример, в случае с числом e (см. пример 67, стр. 107).
Определение 45 (монотонные последовательности) Определим сле-
дующие типы последовательностей:
1. Числовая последовательность {x
n
} называется возрастающей, если
каждый последующий ее член строго больше предыдущего:
x
1
<x
2
<x
3
< ···<x
n
<...

106 Глава 5. Математический анализ
2. Числовая последовательность {x
n
} называется неубывающей, если каж-
дый последующий ее член не меньше предыдущего:
x
1
≤ x
2
≤ x
3
≤···≤x
n
≤ ...
3. Числовая последовательность {x
n
} называется убывающей, если каж-
дый последующий ее член строго меньше предыдущего:
x
1
>x
2
>x
3
> ···>x
n
>...
4. Числовая последовательность {x
n
} называется невозрастающей, если
каждый последующий ее член не больше предыдущего:
x
1
≥ x
2
≥ x
3
≥···≥x
n
≥ ...
Последовательности, являющиеся возрастающими, неубывающими, убыва-
ющими или невозрастающими имеют общее название: они называются мо-
нотонными.
Пример 66 Проиллюстрируем данное определение примерами:
1. Последовательность x
n
=lnn является возрастающей, так как, в силу из-
вестного свойства логарифмической функции, большему значению аргумен-
та отвечает большее значение функции.
2. Последовательность x
n
=
n/2
является неубывающей
5
:
x
1
=0≤ x
2
=1≤ x
3
=1≤ x
4
=2≤ x
5
=2≤ ...
3. Последовательность x
n
=1/n является убывающей, так как большему зна-
чению знаменателя отвечает меньшее значение дроби.
4. Последовательность x
n
, определенная следующим образом
x
1
=1,x
2
=0,x
3
=0,x
4
=0, ... ,
является, очевидно, невозрастающей.
5. Наконец, последовательность x
n
=(−1)
n
не является монотонной, так как
не относится ни к одному из перечисленных типов (ее членами служат че-
редующиеся 1 и − 1).
Теорема 46 (о монотонной ограниченной последовательности)
Если последовательность является монотонной и ограниченной, то она схо-
дится.
Доказательство Ограничимся случаем, когда последовательность {x
n
}
является возрастающей (остальные случаи разбираются аналогично). В этом
случае
x
1
<x
2
<x
3
< ···<x
n
<...
С другой стороны, так как последовательность {x
n
} ограничена, то (см.
опр. 42, стр. 97) существует такое число M ,что
x
1
<x
2
<x
3
< ···<x
n
< ···<M.
5
Здесь квадратные скобки означают целую часть дробного числа.
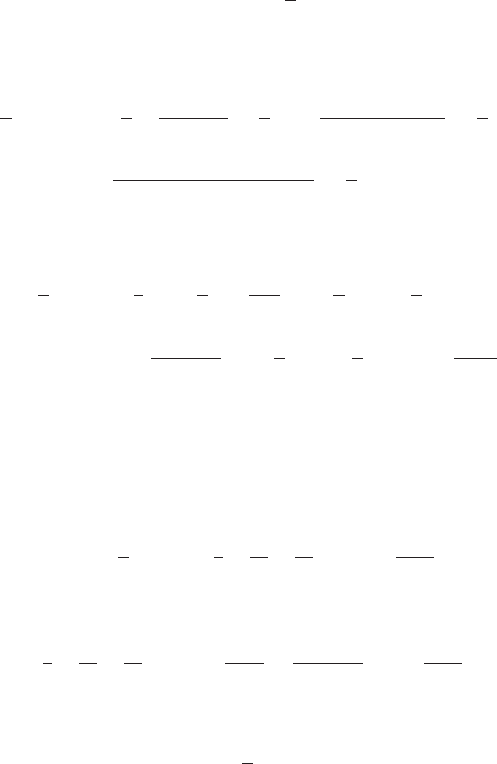
5.1. Пределы. Непрерывность функций 107
Выберем из таких верхних границ наименьшую и обозначим ее a.Тогда
в любой ее окрестности за счет возрастания последовательности {x
n
} на-
ходится бесконечное число членов последовательности. Это означает (см.
опр. 39, стр. 96), что последовательность {x
n
} сходится, и ее пределом слу-
жит число a.
Теорема доказана.
Доказанная теорема находит широкое применение во всем курсе математи-
ческого анализа. Проиллюстрируем ее применение следующим примером.
Пример 67 (число e) Здесь мы убедимся в том, что последовательность
x
n
=
1+
1
n
n
является сходящейся, причем ее предел заключен между 2 и 3. Воспользуемся
формулой бинома Ньютона:
1+
1
n
n
=1+n ·
1
n
+
n(n −1)
1 ·2
·
1
n
2
+
n(n −1)(n − 2)
1 ·2 · 3
·
1
n
3
+ ···
··· +
n(n −1) ···(n − (n − 1))
1 ·2 · 3 ···n
·
1
n
n
.
Выполняя элементарные алгебраические преобразования в каждом слагаемом по-
лучим:
1+
1
n
n
=2+
1
2
1 −
1
n
+
1
2 ·3
1 −
1
n
1 −
2
n
+ ···
··· +
1
2 ·3 ···n
1 −
1
n
1 −
2
n
···
1 −
n −1
n
.
Все слагаемые в этой формуле положительны, причем с возрастанием показателя
n растет и число слагаемых. Следовательно, последовательность {x
n
}, ничиная с
наименьшего значения, равного 2, растет вместе с показателем n.
С другой стороны, очевидно, что каждое слагаемое в сумме увеличится, если
все множители знаменателей заменить на 2, а каждую из скобок заменить на 1.
Поэтому:
1+
1
n
n
< 2+
1
2
+
1
2
2
+
1
2
3
+ ··· +
1
2
n−1
.
В силу известной формулы для вычисления суммы геометрической прогрессии,
мы можем оценить сумму в правой части неравенства:
2+
1
2
+
1
2
2
+
1
2
3
+ ··· +
1
2
n−1
=
1 −1/2
n
1 −1/2
=1−
1
2
n−1
< 1 .
Отсюда, интересующее нас выражение не может возрастать неограниченно, оно
ограничено сверху тройкой:
1+
1
n
n
< 3 .
Таким образом, члены последовательности {x
n
} при возрастании n постояно воз-
растают, оставаясь больше 2 и меньше 3. Отсюда, на основании теоремы о моно-
тонной ограниченной последовательности (см. теор. 46, стр. 106) можно сделать
вывод, что последовательность {x
n
} сходится, причем ее предел заключен между
2и3.

108 Глава 5. Математический анализ
Этот предел и называется числом e:
lim
n→∞
1+
1
n
n
= e.
Его точное значение не выражается в десятичных или рациональных дробях, од-
нако приближенное значение можно вычислить с любой точностью:
e =2. 7182818284 ...
5.1.5 Предел функции
Исторически сложилось так, что примерно в одно и то же время было дано
два определения предела функции: определение Коши и определение Гейне.
Эти определения эквивалентны (см. теор. 47, стр. 109). В зависимости от
ситуации, используется то из них, которое удобнее для решения конкретной
задачи.
Мы так же в ряде случаев будем использовать определение Коши, а в ряде
случаев — определение Гейне.
Определение 46 (предел функции (Гейне)) Число A называется пре-
делом функции f (x) в точке a, если для любой последовательности аргу-
ментов {x
n
}, сходящейся к a, соответствующая последовательность значе-
ний функции {f(x
n
)} сходится к A. Этот факт обозначается следующим
образом:
lim
x→a
f(x)=A.
Пример 68 Покажем, например, пользуясь определением Гейне, что
lim
x→1
(x
2
+ x +1)=3.
Рассмотрим произвольную последовательность {x
n
}, сходящуюся к 1, и соответ-
ствующую ей последовательность {x
2
n
+ x
n
+1} значений функции. Пользуясь
свойствами сходящихся последовательностей (см. теор. 43, 44, стр. 102, 103), по-
лучим:
lim
n→∞
(x
2
n
+ x
n
+ 1) = ( lim
n→∞
x
n
)
2
+ lim
n→∞
x
n
+1=1+1+1=3.
В силу определения Гейне предела функции (см. опр. 46, стр. 108), это означает,
что
lim
x→1
(x
2
+ x +1)=3.
Определение 47 (предел функции (Коши)) Число A называется пре-
делом функции f(x) в точке a, если для любого, сколь угодно малого по-
ложительного ε существует такая δ-окрестность точки a,что
|f(x) − A| <ε для любого x из этой окрестности .
Так же, как и выше, этот факт обозначается следующим образом:
lim
x→a
f(x)=A.

5.1. Пределы. Непрерывность функций 109
Пример 69 Покажем, пользуясь определением Коши, что
lim
x→2
x
2
=4.
По контексту задачи переменная x принимает значения, близкие к 2. Поэтому
можно считать, что 1 <x<3,тоесть—|x − 2| < 1.
Пусть ε — произвольное положительное число. Мы можем оценить разность |x
2
−
4| следующим образом:
|x
2
− 4| = |x − 2||x +2| = |x − 2|(x +2)< 5|x − 2|.
Следовательно, |x
2
− 4| <ε, если |x − 2| <ε/5. Обозначим δ = ε/5. Тогда оказы-
вается, что для любого положительного ε существует положительное δ такое, что
|x
2
− 4| <εдля любого x, попадающего в δ-окрестность точки 2.
Отсюда, в силу определения Коши предела функции в точке (см. опр. 47, стр. 108),
заключаем:
lim
x→2
x
2
=4.
Отметим еще раз, что определения Коши и Гейне являются эквивалентны-
ми (то есть определяют одно и то же понятие), в виде следующей теоремы,
которую примем без доказательства.
Теорема 47 Определения Коши (см. опр. 47, стр. 108) и Гейне (см. опр. 46,
стр. 108) предела функции в точке являются эквивалентными.
Далее нас будут интересовать свойства пределов функций. Отметим, за-
бегая вперед, что они окажутся полностью аналогичны соответствующим
свойствам пределов последовательностей (см. теор. 43, 44 и 45, стр. 102, 103
и 104).
Теорема 48 (свойства пределов функций) Пусть функции f(x) и g(x)
обладают пределами в точке a:
lim
x→a
f(x)=A, lim
x→a
g(x)=B. Тогда:
1. предел суммы функций f(x) и g(x) равен сумме их пределов
lim
x→a
(f(x)+g(x)) = A + B ;
2. предел произведения функций f(x) и g(x) равен произведению их пре-
делов
lim
x→a
(f(x) · g(x)) = A · B,
в частности — постоянный множитель можно выносить из-под знака
предела;
3. если, кроме того, B =0, то предел частного функций f(x) и g(x) равен
частному их пределов:
lim
x→a
f(x)
g(x)
=
A
B
.
110 Глава 5. Математический анализ
Доказательство Докажем первое утверждение (остальные доказываются
аналогично). Воспользуемся определением Гейне предела функции в точке
(см. опр. 46, стр. 108).
Пусть {x
n
} — произвольная последовательность, сходящаяся к a.Тогда
соответствующая последовательность значений функции f(x)+g(x) —это
f(x
n
)+g(x
n
). Пользуясь тем, что предел суммы последовательностей равен
сумме их пределов (см. теор 43, стр. 102), получим:
lim
n→∞
(f(x
n
)+g(x
n
)) = lim
n→∞
f(x
n
) + lim
n→∞
g(x
n
)=A + B.
Таким образом, для любой последовательности {x
n
}, сходящейся к a, соот-
ветствующая последовательность значений функции f(x)+g(x) сходится к
A + B. В силу определения Гейне (см. опр. 46, стр. 108) это означает, что
lim
x→a
(f(x)+g(x)) = A + B.
Теорема доказана.
Теорема 49 (о промежуточной функции) Пусть в некоторой окрест-
ности точки a функция f(x) заключена между двумя функциями ϕ(x) и
ψ(x), имеющими одинаковый предел A, то есть
ϕ(x) ≤ f (x) ≤ ψ(x) , lim
x→a
ϕ(x) = lim
x→a
ψ(x)=A.
Тогда функция f (x) имеет в точке a предел, причем, он тоже равен A:
lim
x→a
f(x)=A.
Доказательство Здесь мы воспользуемся определением Коши предела
функции в точке (см. опр. 47, стр. 108).
Имееющееся по условию теоремы двойное неравенство можно преобразо-
вать, отняв от каждой его части число A:
ϕ(x) − A ≤ f(x) − A ≤ ψ(x) − A.
Отсюда, пользуясь свойствами модуля, заключаем:
(∗) |f(x) − A|≤max{|ϕ − A|, |ψ − A|}.
Так как функции ϕ(x) и ψ(x) имеют в точке a предел, равный A,наос-
новании определения Коши (см. опр. 47, стр. 108) имеем: для любого по-
ложительного ε существует такая δ-окрестность точки a, что одновременно
|ϕ(x) − A| <εи |ψ(x) − A| <εдля любого x, попадающего в δ-окрестность
точки a.
Отсюда, на основании соотношения (∗), заключаем: для любого положи-
тельного ε существует такая δ-окрестность точки a,что
|f(x) − A| <ε, для любого x из этой δ-окрестности.
По определению Коши (см. опр. 47, стр. 108) это в точности означает, что
lim
x→a
f(x)=A.
Теорема доказана.
