Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

6.3. Пример алгоритма интерполяции 151
— для первого координатного полинома и, аналогично, для второго:
b
20
b
21
b
22
b
23
=
1000
0010
−33−2 −1
2 −211
4
2
−5
0
=
4
−5
4
−1
.
Таким образом, интересующая нас параметризация найдена:
q(u)=
1+3· u
2
− u
3
4 − 5 · u +4· u
2
− u
3
.
Теперь, придавая параметру u значения от 0 до 1 с шагом 0. 1,мыможем
вычислить координаты траектории точки M . Стартовая точка получается
при нулевом значении праметра u =0:
M
0
= p(0) =
−1 − 3. 536 · 0+13. 072 · 0
2
− 7. 536 · 0
3
3+3. 536 · 0 − 0. 928 · 0
2
− 3. 464 · 0
3
=
−1
3
= A.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 1:
M
1
= p(0. 1) =
=
−1 − 3. 536 · 0. 1+13. 072 · 0. 1
2
− 7. 536 · 0. 1
3
3+3. 536 · 0. 1 − 0. 928 · 0. 1
2
− 3. 464 · 0. 1
3
=
−1. 23
3. 359
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 2:
M
2
= p(0. 2) =
=
−1 − 3. 536 · 0. 2+13. 072 · 0. 2
2
− 7. 536 · 0. 2
3
3+3. 536 · 0. 2 − 0. 928 · 0. 2
2
− 3. 464 · 0. 2
3
=
−1. 245
3. 717
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 3:
M
3
= p(0. 3) =
=
−1 − 3. 536 · 0. 3+13. 072 · 0. 3
2
− 7. 536 · 0. 3
3
3+3. 536 · 0. 3 − 0. 928 · 0. 3
2
− 3. 464 · 0. 3
3
=
−1. 088
4. 051
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 4:
M
4
= p(0. 4) =
=
−1 − 3. 536 · 0. 4+13. 072 · 0. 4
2
− 7. 536 · 0. 4
3
3+3. 536 · 0. 4 − 0. 928 · 0. 4
2
− 3. 464 · 0. 4
3
=
−0. 805
4. 341
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 5:
M
5
= p(0. 5) =
−1 − 3. 536 · 0. 5+13. 072 · 0. 5
2
− 7. 536 · 0. 5
3
3+3. 536 · 0. 5 − 0. 928 · 0. 5
2
− 3. 464 · 0. 5
3
=
−0. 442
4. 576
.
152 Глава 6. Интерполяция кривых
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 6:
M
6
= p(0. 6) =
=
−1 − 3. 536 · 0. 6+13. 072 · 0. 6
2
− 7. 536 · 0. 6
3
3+3. 536 · 0. 6 − 0. 928 · 0. 6
2
− 3. 464 · 0. 6
3
=
−0. 043
4. 707
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 7:
M
7
= p(0. 7) =
=
−1 − 3. 536 · 0. 7+13. 072 · 0. 7
2
− 7. 536 · 0. 7
3
3+3. 536 · 0. 7 − 0. 928 · 0. 7
2
− 3. 464 · 0. 7
3
=
0. 345
4. 742
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 8:
M
8
= p(0. 8) =
=
−1 − 3. 536 · 0. 8+13. 072 · 0. 8
2
− 7. 536 · 0. 8
3
3+3. 536 · 0. 8 − 0. 928 · 0. 8
2
− 3. 464 · 0. 8
3
=
0. 679
4. 649
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 9:
M
9
= p(0. 9) =
=
−1 − 3. 536 · 0. 9+13. 072 · 0. 9
2
− 7. 536 · 0. 9
3
3+3. 536 · 0. 9 − 0. 928 · 0. 9
2
− 3. 464 · 0. 9
3
=
0. 912
4. 409
.
Следующая точка траектории получается при очередном значении прамет-
ра u =1:
M
10
= p(1) =
−1 − 3. 536 · 1+13. 072 · 1
2
− 7. 536 · 1
3
3+3. 536 · 1 − 0. 928 · 1
2
− 3. 464 · 1
3
=
1
4
= B.
Итак, мы получили точки первого сегмента траектории. Второй сегмент
параметризован нами при помощи функции q(u). Очередная точка траек-
тории получается при значении параметра u =0, 1:
M
11
= q(0. 1) =
1+3· 0. 1
2
− 0. 1
3
4 − 5 · 0. 1+4· 0. 1
2
− 0. 1
3
=
1. 029
3. 359
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 2:
M
12
= q(0. 2) =
1+3· 0. 2
2
− 0. 2
3
4 − 5 · 0. 2+4· 0. 2
2
− 0. 2
3
=
1. 112
3. 152
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 3:
M
13
= q(0. 3) =
1+3· 0. 3
2
− 0. 3
3
4 − 5 · 0. 3+4· 0. 3
2
− 0. 3
3
=
1. 243
2. 833
.
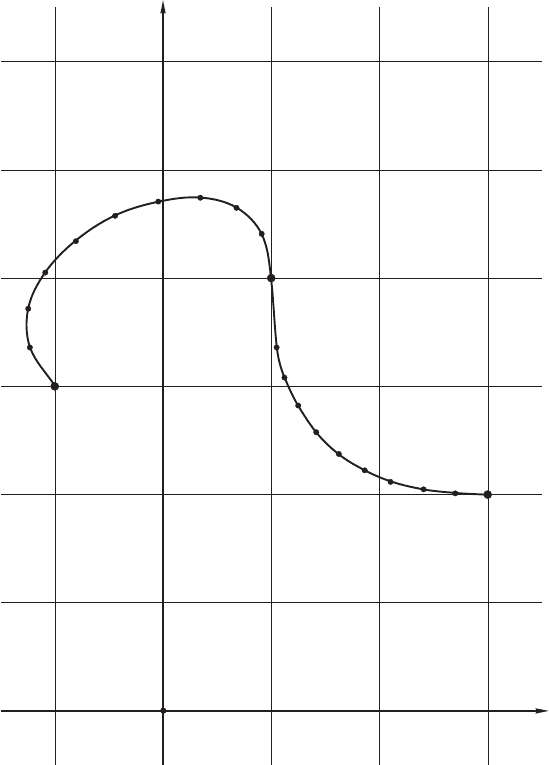
6.3. Пример алгоритма интерполяции 153
x
y
0
A
B
C
Рис. 6.5: Два сегмента кривой, гладко сопряженные в точке B.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 4:
M
14
= q(0. 4) =
1+3· 0. 4
2
− 0. 4
3
4 − 5 · 0. 4+4· 0. 4
2
− 0. 4
3
=
1. 416
2. 576
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 5:
M
15
= q(0. 5) =
1+3· 0. 5
2
− 0. 5
3
4 − 5 · 0. 5+4· 0. 5
2
− 0. 5
3
=
1. 625
2. 375
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 6:
M
16
= q(0. 6) =
1+3· 0. 6
2
− 0. 6
3
4 − 5 · 0. 6+4· 0. 6
2
− 0. 6
3
=
1. 864
2. 224
.
154 Глава 6. Интерполяция кривых
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 7:
M
17
= q(0. 7) =
1+3· 0. 7
2
− 0. 7
3
4 − 5 · 0. 7+4· 0. 7
2
− 0. 7
3
=
2. 127
2. 117
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 8:
M
18
= q(0. 8) =
1+3· 0. 8
2
− 0. 8
3
4 − 5 · 0. 8+4· 0. 8
2
− 0. 8
3
=
2. 408
2. 048
.
Следующая точка траектории получается при очередном значении прамет-
ра u =0, 9:
M
19
= q(0. 9) =
1+3· 0. 9
2
− 0. 9
3
4 − 5 · 0. 9+4· 0. 9
2
− 0. 9
3
=
2. 701
2. 011
.
Следующая точка траектории получается при очередном значении прамет-
ра u =1:
M
20
= q(1) =
1+3· 1
2
− 1
3
4 − 5 · 1+4· 1
2
− 1
3
=
3
2
= C.
Понятно, что с точки зрения современного процессора совершенно безраз-
лично, какое именно количество точек требуется изобразить на кривой: два-
дцать , как в нашем примере, или несколько тысяч. Тем самым, достигает-
ся возможность построить визуально гладкую кривую за счет достаточно
длинного цикла вычислений (см. рис. 6.5, стр. 153).
Часть III
Приложения
155

Приложение A
Определители, матрицы и
линейные системы
Вычислительная техника линейной алгебры базируется на элементарных
преобразованиях строк (реже — столбцов) матриц, определителей или ли-
нейных систем. Элементарные преобразования, сведенные в единую лако-
ничную систему действий, именуются методом Гаусса решения той или иной
задачи.
В рамках этого раздела, посвященного определителям, матрицам и линей-
ным системам, при помощи метода Гаусса мы будем вычислять: опреде-
лители (см. раздел A.1.2, стр. 159), обратные матрицы (см. раздел A.2.2,
стр. 167) и решения линейных систем (см. раздел A.3.2, стр. 177). И хотя,
в приложении к каждому из этих трех типов задач, метод Гаусса обладает
своей спецификой, отличия эти незначительны и носят скорее косметиче-
ский характер.
В любом случае, метод Гаусса — это вычислительный фундамент линейной
алгебры.
A.1 Определители
Матрицы, с изучения которых мы начинаем курс линейной алгебры (см.
главу 2, стр. 17), обладают несколькими числовыми характеристиками
1
,
одной из которых является ее определитель.
A.1.1 Определители второго и третьего порядков
Подробное изложение теории определителей выходит за рамки нашего крса,
однако техника их вычисления лежит в основе очень многих алгебраиче-
ских задач. В этом разделе мы рассмотрим простейшие ситуации (определи-
тели 2-го и 3-го порядков) и подробно разберем вычислительные примеры.
1
Так же, как например, векторы: вектор, описаный в координатах — это набор чисел,
а его длина — число, причем, положительное. Длина вектора — это одна из его числовых
характеристик.
157

158 Приложение A. Определители, матрицы и линейные системы
Определение 66 (определители 2-го порядка) Пусть имеется матри-
ца A из полной матричной алгебры 2-го порядка: A ∈ Matr
2
. Ее определи-
телем называется число, вычисляемое по следующей формуле:
ab
cd
= ad − bc.
Определитель матрицы обозначается |A| или det A (от латинского слова
determinant).
Пример 95
25
43
=2· 3 − 5 · 4=−14.
Пример 96
1 −3
25
=1· 5 − (−3) · 2=11.
Пример 97
cos α −sin α
sin α cos α
=cos
2
α +sin
2
α =1.
Ничего сложного. Поэтому перейдем к определителям третьего порядка.
Здесь вычислительная сложность возрастет.
Определение 67 (определители 3-го порядка) Пусть имеется матри-
ца A из полной матричной алгебры 3-го порядка: A ∈ Matr
3
. Ее определи-
телем называется число, вычисляемое по следующей формуле:
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
=
a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
−a
13
a
22
a
31
− a
11
a
23
a
32
− a
12
a
21
a
33
.
Так же, как и в случае матриц 2 × 2, определитель матрицы третьего по-
рядка обозначается |A| или det A.
Прокомментирем формулу. Это – сумма, состоящая из шести слагаемых,
причем часть из них входит в формулу со знаком “плюс”, а часть — со
знаком “минус” (другими словами, имеются две серии слагаемых: положи-
тельная и отрицательная). Каждое слагаемое — это произведение трех мно-
жителей, у которых первые индексы следуют по порядку, а вторые — пере-
мешаны всеми возможными способами.
Для запоминания этой формулы применяют мнемоническое правило, назы-
ваемое правилом треугольников (или правилом Саррюса
2
).
+ К положительной серии слагаемых относятся: произведение элемен-
тов главной диагонали и произведения матричных элементов, распо-
ложенных в вершинах треугольников с основаниями, параллельными
главной диагонали.
− К отрицательной серии слагаемых относятся: произведение элементов
побочной диагонали и произведения матричных элементов, располо-
женных в вершинах треугольников с основаниями, параллельными
побочной диагонали.
2
Математик, который придумал это правило и больше, кажется, ничем не прославил-
ся.

A.1. Определители 159
Пример 98 Применяя правило Саррюса, вычислим определитель третьего по-
рядка:
13−2
20 1
45 1
=
1 ·0 · 1+3· 1 ·4+(−2) · 2 · 5−
−1 ·1 · 5 − 3 · 2 · 1 −(−2) · 0 · 4
=
=
12 −20 − 5 − 6=−19.
Пример 99 Рассмотрим еще один числовой пример:
−312
114
211
=
(−3) ·1 · 1+1· 4 ·2+2· 1 · 1−
−(−3) ·4 · 1 − 1 · 1 · 1 − 2 · 1 · 2
=
=
−3+8+2+12− 1 − 4=14.
Пример 100 Элементами определителя могут быть не только числа, но и функ-
циональные выражения, зависящие от переменных. Как, например, здесь:
α
2
+1 αβ αγ
αβ β
2
+1 βγ
αγ βγ γ
2
+1
=
=(α
2
+1)(β
2
+1)(γ
2
+1)+α
2
β
2
γ
2
+ α
2
β
2
γ
2
− (α
2
+1)β
2
γ
2
−
− (γ
2
+1)α
2
β
2
− (β
2
+1)α
2
γ
2
=
= α
2
β
2
γ
2
+ α
2
γ
2
+ β
2
γ
2
+ γ
2
+ α
2
β
2
+ α
2
+ β
2
+1−
− α
2
β
2
γ
2
− β
2
γ
2
− α
2
β
2
− α
2
γ
2
=
= α
2
+ β
2
+ γ
2
+1.
Все получается после раскрытия скобок и приведения подобных членов.
Вычисление определителя по определению — это не самый удобный метод
вычисления определителей. Имеются методы, альтернативные ему, их мы
рассмотрим в следующем разделе.
A.1.2 Свойства определителей
Метод Гаусса, состоящий в элементарных преобразованиях строк или столб-
цов определителя
3
, основан на его свойствах. Мы сформулируем их в виде
следующей теоремы.
Теорема 85 (свойства определителя) Определитель любой матрицы об-
ладает следующими свойствами:
1. |A
T
| = |A| — то есть определитель матрицы не изменяется при ее
транспонировании
4
.
3
Напомним, что метод Гаусса применяется не только для вычисления определителей,
но также для вычисления обратных матриц и для решения линейных систем.
4
Транспонированием называется матричная операция, при которой строки и столбцы
матрицы меняются ролями: первая строка становится первым столбцом, вторая — вто-
рым столбцом и т.д. Это свойство означает, в частности, что все свойства определителя,
верные для его строк, верны также и для столбцов. Все дальнейшие свойства опреде-
лителя мы сформулируем именно для строк, подразумевая, что аналогичные свойства
имеются и для столбцов.

160 Приложение A. Определители, матрицы и линейные системы
2. Определитель верхней (или нижней) треугольной матрицы равен про-
изведению элементов ее главной диагонали.
3. Если в определителе поменять местами две строки, то определитель
сменит знак.
4. Общий множитель строки можно выносить из-под знака определите-
ля.
5. Определитель не изменится, если к одной его строке прибавить дру-
гую, домноженную на число
5
.
6. Определитель, содержащий нулевую строку, равен нулю.
7. Определитель, содержащий две одинаковые строки, равен нулю.
8. Определитель, содержащий две пропорциональные строки, равен ну-
лю.
При помощи свойств определителя его можно преобразовать к верхнему
(или нижнему — как удобно) треугольному виду, после чего — восполь-
зоваться тем фактом, что определитель треугольной матрицы равен про-
изведению элементов ее главной диагонали. В этом состоит метод Гаусса
вычисления определителей.
Пример 101
10−2
22 1
−13 2
−I ∗2
+I
=
10−2
02 5
03 0
=3
10−2
02 5
01 0
← III
← II
=
= −3
10−2
01 0
02 5
−II ∗ 2
= −3
10−2
01 0
00 5
= −3 ·(1 · 1 · 5) = −15.
Прокомментируем выкладу. Итак, нашей целью является построение нулей на
всех местах матрицы, расположенных ниже главной диагонали (тогда матрица
приобретет верхний треугольный вид).
На первом шаге мы от второй строки определителя отнимаем первую строку, до-
множив ее на 2, и к третьей строке прибавляем первую же. Отметим, что при
этом первая строка остается без изменения, а вторая и третья строки — преоб-
разуются. После этих действий на первых местах во второй и в третьей строках
появляются нулевые элементы.
На втором шаге мы из третьей строки выносим 3 за знак определителя как общий
множитель строки.
На третьем шаге мы меняем местами вторую и третью строки. При этом опреде-
литель меняет знак.
На четвертом шаге мы отнимаем от третьей строки вторую, домножив ее на 2, для
того, чтобы получить еще один 0 ниже главной диагонали. Отметим еще раз: при
этом действии вторая строка не изменяется, преобразуется только третья строка.
После этого определитель приобретает верхний треугольный вид и вычисляется
уже очень легко: произведением элементов главной диагонали.
5
В более общем случае — определитель не изменится, если к его строке прибавить
любую линейную комбинацию других строк.
