Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

B.3. Проективные операторы 201
ективным координатам (см. определение 83 на стр. 199):
A
= η (A)=
0 −1 −3
101
001
1
1
1
=
−4
2
1
, таким образом, A
(−4, 2) ;
B
= η (B)=
0 −1 −3
101
001
1
2
1
=
−5
2
1
, и, значит, B
(−5, 2) ;
C
= η (C)=
0 −1 −3
101
001
3
1
1
=
−4
4
1
, следовательно, C
(−4, 4) .
Пример 140 Треугольник с вершинами A(1, 3), B(5, 2), C(3, 4) равномерно мас-
штабируется относительно вершины C с коэффициентом 2 (см. рис. B.1, стр. 200).
Найти координаты вершин результирующего треугольника A
B
C
.
Масштабирование плоскости как линейный оператор возможно только относи-
тельно начала координат. Поэтому для реализации нужного нам плоского преоб-
разования η в матричной форме необходимо сначала сместить центр масштаби-
рования C(3, 4) в начало координат, на вектор b = {−3, −4} (тоесть—выпол-
нить трансляцию T
b
), затем выполнить равномерное двукратное масштабирова-
ние плоскости S
2
и наконец — выполнить обратное смещение: трансляцию T
−b
на
вектор −b = {3, 4}.
η = T
−b
S
2
T
b
=
103
014
001
200
020
001
10−3
01−4
00 1
=
20−3
02−4
00 1
Теперь можно вычислить координаты результирующего треугольника просто при
помощи матричного умножения: для этого нужно предварительно перейти к про-
ективным координатам (см. определение 83 на стр. 199):
A
= η (A)=
20−3
02−4
00 1
1
3
1
=
−1
2
1
, таким образом, A
(−1, 2) ;
B
= η (B)=
20−3
02−4
00 1
5
2
1
=
7
0
1
, и, значит, B
(7, 0) ;
C
= η (C)=
20−3
02−4
00 1
3
4
1
=
3
4
1
, следовательно, C
(3, 4) .
Как и следовало ожидать, центр масштабирования под его действием перешел в
себя.
Пример 141 Треугольник с вершинами A(4, 2), B(4, 4), C(6, 2) симметрично от-
ражается относительно точки G(1, 3) (см. рис. B.2, стр. 202). Найти координаты
вершин результирующего треугольника A
B
C
.
Симметричное отражение плоскости относительно начала координат — это то же
самое, что и поворот на π (или равномерное масштабирование с коэффициентом
(−1) — как угодно). Поэтому для реализации нужного нам плоского преобразо-
вания η в матричной форме необходимо сначала сместить центр симметрии (мас-
штабирования или поворота — как угодно) G(1, 3) в начало координат, на вектор
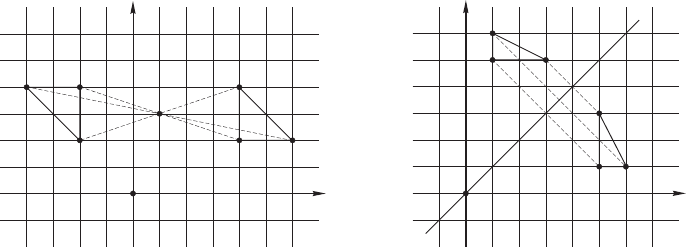
202 Приложение B. Векторные пространства
x
y
0
G
(a) Симметричное отражение относитель-
но некоторой точки G.
x
y
0
l
(b) Симметричное отражение отно-
сительно наклонной оси l.
Рис. B.2: Примеры проективных преобразования плоскости.
b = {−1, −3} (то есть — выполнить трансляцию T
b
), затем выполнить равномер-
ное масштабирование плоскости S
−1
(или поворот R
π
) и наконец — выполнить
обратное смещение: трансляцию T
−b
на вектор −b = {1, 3}.
η = T
−b
S
−1
T
b
=
101
013
001
−100
0 −10
001
10−1
01−3
00 1
=
=
−102
0 −16
001
.
Теперь можно вычислить координаты результирующего треугольника просто при
помощи матричного умножения: для этого нужно предварительно перейти к про-
ективным координатам (см. определение 83 на стр. 199):
A
= η (A)=
−102
0 −16
001
4
2
1
=
−2
4
1
, таким образом, A
(−2, 4) ;
B
= η (B)=
−102
0 −16
001
4
4
1
=
−2
2
1
, и, значит, B
(−2, 2) ;
C
= η (C)=
−102
0 −16
001
6
2
1
=
−4
4
1
, следовательно, C
(−4, 4) .
Пример 142 Треугольник с вершинами A(5, 1), B(5, 3), C(6, 1) симметрично от-
ражается относительно прямой l : y = x (см. рис. B.2, стр. 202). Найти координаты
вершин результирующего треугольника A
B
C
.
Выше мы отнесли к основным плоским преобразованиям симметричные отраже-
ния Q
x
, Q
y
плоскости относительно координатных осей. Поэтому для реализации
нужного нам плоского преобразования η в матричной форме необходимо сначала
повернуть плоскость так, чтобы прямая l совпала с одной из осей. Можно, на-
пример, выполнить сначала поворот R
−π/4
на угол −π/4, добившись тем самым

B.4. Задачи для самостоятельного решения 203
совмещения прямой l с осью x, затем выполнить отражение Q
x
относительно этой
оси и, наконец, выполнить обратный поворот R
π/4
плоскости на угол π/4.
η = R
π/4
Q
x
R
−π/4
=
=
√
2/2 −
√
2/20
√
2/2
√
2/20
001
100
0 −10
001
√
2/2
√
2/20
−
√
2/2
√
2/20
001
=
=
010
100
001
.
Теперь можно вычислить координаты результирующего треугольника просто при
помощи матричного умножения для этого нужно предварительно перейти к про-
ективным координатам (см. определение 83 на стр. 199):
A
= η (A)=
010
100
001
5
1
1
=
1
5
1
, таким образом, A
(1, 5) ;
B
= η (B)=
010
100
001
5
3
1
=
3
5
1
, и, значит, B
(3, 5) ;
C
= η (C)=
010
100
001
6
1
1
=
1
6
1
, следовательно, C
(1, 6) .
B.4 Задачи для самостоятельного решения
Задача 14 Определить, являются следующие системы векторов линейно зави-
симыми или линейно независимыми (см. опр. 75, стр. 188 и соответствующие
примеры):
1) v
1
=(1, 1, −1) ,
v
1
=(0, 1, 1) ,
v
1
=(1, 2, 0) ;
2) v
1
=(−3, 0, 2) ,
v
1
=(1, 1, 1) ,
v
1
=(1, 2, 1) ;
3) v
1
=(1, 1, 1) ,
v
1
=(2, 1, −1) ,
v
1
=(−1, 0, 2) .
Задача 15 Пусть на плоскости R
2
фиксирован базис e
1
,e
2
, и пусть в этом базисе
векторы f
1
,f
2
и h
1
,h
2
имеют известные разложения. Пусть, кроме того, известны
координаты x
F
вектора x в базисе f
1
,f
2
:
1) f
1
= e
1
+ e
2
,h
1
= − e
2
,x
F
=(1, 1) ;
f
2
= e
2
; h
2
= e
1
+ e
2
;
2) f
1
= e
1
− e
2
,h
1
= e
1
+ e
2
,x
F
=(−1, 0) ;
f
2
= e
1
; h
2
= e
2
;
3) f
1
= e
1
+ e
2
,h
1
= e
1
− e
2
,x
F
=(2, 1) .
f
2
= e
1
− e
2
; h
2
= e
2
;
Вычислить координаты x
H
вектора x в базисе h
1
,h
2
(см. теор. 93, стр. 191 и
соответствующие примеры).
204 Приложение B. Векторные пространства
Задача 16 Оператор ϕ действует в трехмерном пространстве R
3
, переводя век-
торы a
i
в векторы b
i
(i =1, 2, 3):
1) a
1
=(1, −1, 3) ,b
1
=(3, 5, 2) ,
a
2
=(0, 1, 4) ,b
2
=(3, 3, 0) ,
a
3
=(0, 0, −1) ,b
3
=(4, 1, 2) ;
2) a
1
=(0, −1, 0) ,b
1
=(2, 1, 1) ,
a
2
=(0, 1, 4) ,b
2
=(3, 3, 4) ,
a
3
=(1, 0, −1) ,b
3
=(1, 1, 2) ;
3) a
1
=(−1, 1, 4) ,b
1
=(1, 1, 2) ,
a
2
=(0, 1, 2) ,b
2
=(3, 3, 1) ,
a
3
=(0, 0, −1) ,b
3
=(4, −1, 1) .
Вычислить матрицу оператора ϕ в том базисе, в котором указаны координаты
всех векторов (см. опр. 81, стр. 194 и соответствующие примеры).
Для решения следующих задач воспользуйтесь результатами, полученными в раз-
деле B.3, стр. 198.
Задача 17 Треугольник ABC поворачивается относительно точки H на угол α.
Вычислить координаты вершин результирующего треугольника, если:
1) A(5, 3) ,B(5, 6) ,C(7, 3) ,H(3, 2) ,α= π/2;
2) A(−3, 3) ,B(−1, 5) ,C(−1, 3) ,H(−1, 2) ,α= −π/2;
3) A(3, −3) ,B(3, −1) ,C(5, −1) ,H(2, −1) ,α=3π/2 .
Задача 18 Треугольник ABC равномерно масштабируется относительно точки
H с коэффициентом k. Вычислить координаты вершин результирующего тре-
угольника, если:
1) A(4, 3) ,B(4, 5) ,C(6, 3) ,H(2, 2) ,k=2;
2) A(2, −4) ,B(2, −2) ,C(3, −2) ,H(−1, 2) ,k=3;
3) A(−3, 3) ,B(−1, 3) ,C(−1, 1) ,H(1, 4) ,k=2.
Задача 19 Треугольник ABC симметрично отражается относительно прямой l.
Вычислить координаты вершин результирующего треугольника, если:
1) A(1, 2) ,B(1, 4) ,C(3, 2) ,l: y = −x,
2) A(2, 3) ,B(2, 4) ,C(4, 3) ,l: y = x +2,
3) A(−2, −1) ,B(−2, 1) ,C(0, 1) ,l: y = x −1 .

Приложение C
Функции и графики.
Интерполяция кривых
C.1 Дифференцирование функций
Дифференцирование функций является важнейшим элементом математической
культуры, и, несмотря на то, что в приложениях, посвященных задачам интерпо-
ляции, оно играет весьма незначительную роль, мы уделяем ему большое внима-
ние.
Теоретические основы дифференциального исчисления были получены нами во
второй части книги (см. главу 5, стр. 95). Здесь мы рассмотрим практические
примеры.
C.1.1 Дифференцирование функции, заданной явно.
Простейшие случаи
Определение 85 (производная функции) Производной функции f(x) в точ-
ке x
0
называется предел отношения приращения ∆f функции к приращению ∆x
аргумента x в этой точке:
f
(x
0
) = lim
∆x→0
∆f
∆x
Если такой предел существует, то функция f(x) называется дифференцируемой
в точке x
0
. Если функция дифференцируема в каждой точке некоторого про-
межутка a, b (угловые скобки здесь означают, что промежуток может быть как
замкнутым, так и открытым), то функция f(x) называется дифференцируемой на
промежутке a, b, а ее производной f
(x) на промежутке a, b называется функ-
ция, которая каждой точке промежутка ставит в соответствие значение произ-
водной функции f (x), вычисленное в этой точке.
Операция нахождения по данной функции f(x) ее производной f
(x) называется
дифференцированием функции f(x).
Для того, чтобы полноценно вычислять производные любых явных функций, до-
статочно знать три вещи: таблицу производных простейших элементарных функ-
ций, правила дифференцирования и правило дифференцирования сложной функ-
ции. Напомним, что к простейшим элементарным функциям относятся функции
следующих нескольких типов: степенные функции, показательные функции, ло-
гарифмические функции, тригонометрические функции и обратные тригономет-
205

206 Приложение C. Функции и графики
рические функции. Их производные были получены нами ранее (см. раздел 5.2.3,
стр. 121), здесь мы продублируем этот результат в виде следующей теоремы.
Теорема 96 ( таблица производных ) Простейшие элементарные функции
дифференцируются в соответствии со следующими формулами, которые мы объ-
единили по блокам:
1. Производная константы: C
=0, а также — производная перменной, по
которой ведется дифференцирование: x
=1.
2. Производная степенной функции:
( x
α
)
= αx
α−1
, где α — любое вещественное число;
в частности,
√
x
=
1
2
√
x
,
1
x
= −
1
x
2
.
3. Производные тригонометрических функций синус, косинус, тангенс и ко-
тангенс:
(sinx )
=cosx, (cosx )
= −sin x,
(tgx )
=
1
cos
2
x
, (ctgx )=−
1
sin
2
x
.
4. Производные обратных тригонометрических функций арксинус, арккоси-
нус, арктангенс и арккотангенс:
(arcsinx )
=
1
√
1 −x
2
, ( arccos x )
= −
1
√
1 −x
2
,
(arctgx )
=
1
1+x
2
, ( arcctg x )
= −
1
1+x
2
.
5. Производные показательных и логарифмических функций:
( a
x
)
= a
x
ln a, в частности, ( e
x
)
= e
x
.
(log
a
x )
=
1
x ln a
, в частности, (lnx )
=
1
x
.
Далее вопроизведем еще раз правила дифференцирования, полученные выше в
теоретическом блоке (см. раздел 5.2.2, стр 119), после чего — рассмотрим приме-
ры.
Теорема 97 (правила дифференцирования) Для любых двух дифференци-
руемых функций f(x) и g(x) сраведливы следующие правила дифференцирова-
ния:
1. дифференцирование суммы:
f(x)+g(x)
= f
(x)+g
(x),
2. дифференцирование произведения:
f(x) · g(x)
= f
(x) ·g(x)+f(x) · g
(x)
(в частности, если один из множителей, например f(x), является константой
C,то
·g(x)
= · g
(x), то есть — постоянный множитель можно выносить
из-под знака производной),
3. дифференцирование частного:
f(x)
g(x)
=
f
(x) ·g(x) −f(x) ·g
(x)
g
2
(x)
.
Пример 143 Пусть требуется продифференцировать функцию y:
y =3x
2
+4sinx +
1
5
log
2
x.
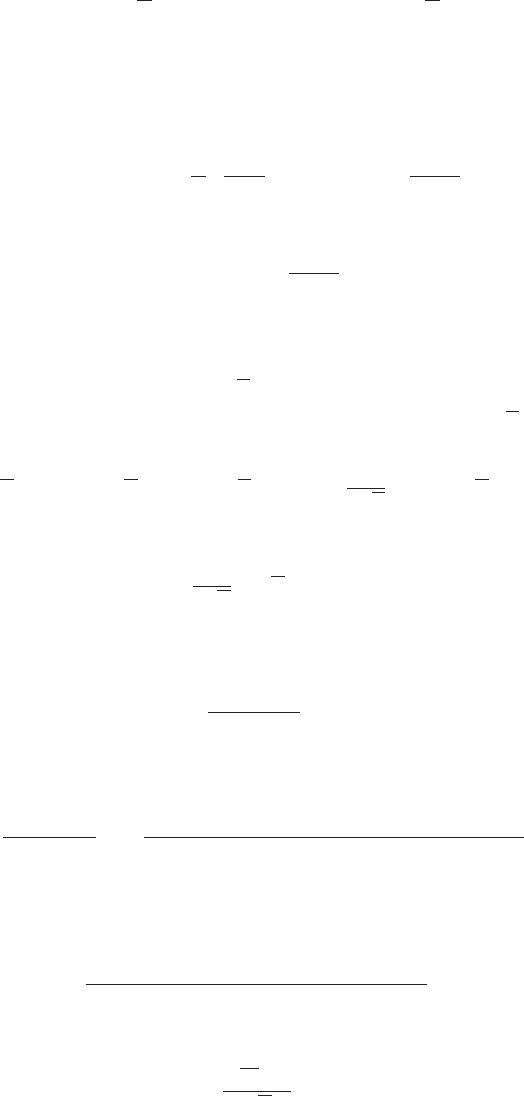
C.1. Дифференцирование функций 207
Прежде всего, воспользуемся правилами дифференцирования (см. теор. 97, стр. 206)
для того, чтобы свести вычисления к табличным производным:
y
=
3x
2
+4sinx +
1
5
log
2
x
=3
x
2
+4(sinx )
+
1
5
(log
2
x )
.
Здесь мы сначала свели дифференцирование суммы к сумме производных, а затем
— вынесли из-под знака производной постоянные множители.
Теперь, согласно таблице производных (см. теор. 96, стр. 206), мы можем вычис-
лить производные каждого слагаемого:
y
=3· 2x +4cosx +
1
5
·
1
x ln 5
=6x +4cosx +
1
x5ln5
.
Таким образом, результатом дифференцирования данной функции y служит сле-
дующая функция y
:
y
=6x +4cosx +
1
x5ln5
.
Пример 144 Приведем пример на применение правила дифференцирования про-
изведения (см. теор. 97, стр. 206). Пусть требуется продифференцировать следу-
ющую функцию:
y =
√
x sin x.
Она представляет собой произведение двух элементарных функций
√
x и sin x.
Поэтому:
y
=
√
x · sin x
=(
√
x )
· sin x +
√
x · (sin x)
=
1
2
√
x
· sin x +
√
x · cos x.
Таким образом, результатом дифференцирования служит следующая функция:
y
=
sin x
2
√
x
+
√
x cos x.
Пример 145 Пусть требуется продифференцировать функцию y,являющуюся
частным двух элементарных функций:
y =
3x
2
+ x − 3
log
5
x
.
Согласно правилу дифференцирования частного (см. теор. 97, стр. 206), мы долж-
ны выполнить следующие действия:
y
=
3x
2
+ x − 3
log
5
x
=
(3x
2
+ x − 3)
· log
5
x −(3x
2
+ x − 3) · (log
5
x)
log
2
5
x
.
Теперь нам нужно выполнить дифференцирование двух скобок в числителе. Вто-
рая из них — это табличная функция, а к первой можно применить правило
дифференцирования суммы (см. теор. 97, стр. 206 и пример 143, стр. 206).
y
=
(6x +1)· log
5
x −(3x
2
+ x − 3) · (1/x ln 5)
log
2
5
x
.
Пример 146 Продифференцируем следующую функцию:
y =
3
√
x
2
− 1
√
x
.
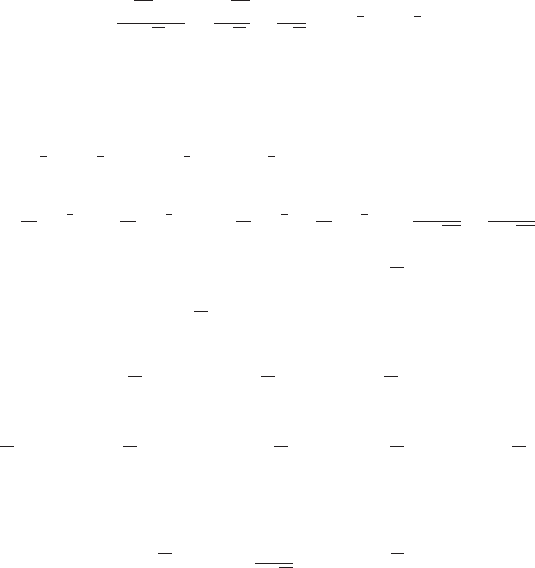
208 Приложение C. Функции и графики
На первый взгляд, эта функция является частным двух функций и, следователь-
но, ее нужно дифференцировать именно как частное согласно правилам диффе-
ренцирования. Действительно, такой подход возможен. Однако в данном случае
удобнее будет предварительно преобразовать дифференцируемую функцию, раз-
делив числитель почленно на знаменатель.
y =
3
√
x
2
− 1
√
x
=
3
√
x
2
√
x
−
1
√
x
= x
−
1
6
− x
−
1
2
.
Теперь дифференцируемая функция — это просто разность двух степенных функ-
ций, каждая из которых дифференцируется очень легко (см. таблицу производ-
ных, теор. 96, стр. 206).
y
=
x
−
1
6
− x
−
1
2
=
x
−
1
6
−
x
−
1
2
=
= −
1
6
x
−
1
6
−1
+
1
2
x
−
1
2
−1
= −
1
6
x
−
7
6
+
1
2
x
−
3
2
= −
1
6
6
√
x
7
+
1
2
√
x
3
.
Пример 147 Продифференцируем функцию y =2
x
√
x sin x. Здесь мы встре-
чаемся с ситуацией, когда дифференцируемая функция является произведением
трех элементарных фукций: 2
x
,
√
x и sin x. Для вычисления производной нам при-
дется дважды применить правило дифференцирования произведения (см. теор. 97,
стр. 206).
y =
2
x
√
x sin x
=
2
x
√
x
sin x +2
x
√
x (sin x)
.
Теперь в первом слагаемом нам нужно снова применить то же правило:
y =
2
x
√
x
sin x +2
x
√
x (sin x)
=(2
x
)
√
x sin x +2
x
(
√
x )
sin x +2
x
√
x (sin x)
.
В итоге, приходим к необходимости взять три табличные (см. теор. 96, стр. 206)
производные.
y =2
x
ln 2
√
x sin x +2
x
1
2
√
x
sin x +2
x
√
x cos x.
C.1.2 Дифференцирование сложной функции
Последним шагом в развитии техники дифференцирования является дифферен-
цирование сложной функции (то есть — суперпозиции простейших элементар-
ных функций). Мы продублируем здесь урверждение, полученное нами выше (см.
теор. 75, стр. 129), после чего рассмотрим примеры.
Теорема 98 (правило дифференцирования сложной функции) Пусть y
— это сложная функциия переменной x:
y = f (u(x)).
Тогда, если функция u является дифференцируемой как функция от перемен-
ной x, а функция f является дифференцируемой как функция переменной u,то
функция y является дифференцируемой как функция переменной x, причем, ее
производная может быть вычислена по следующей формуле:
y
= f
u
(u) ·u
x
(x) ,
то есть, производная сложной функции равна произведению данной функции по
промежуточному аргументу и производной промежуточного аргумента по неза-
висимой переменной.
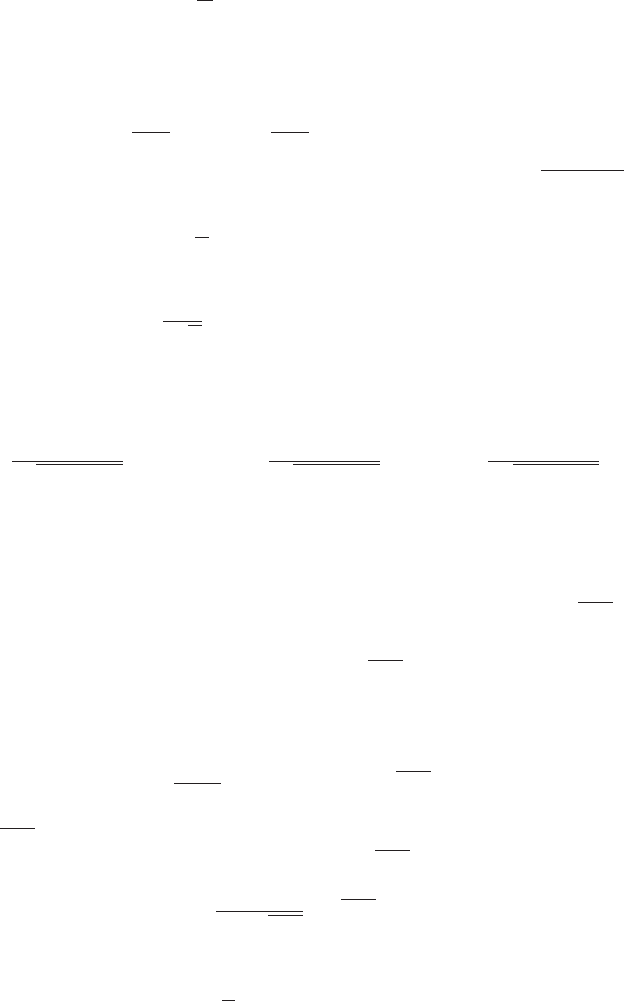
C.1. Дифференцирование функций 209
Пример 148 Пусть требуется продифференцировать сложную функцию y =
ln cos x. Мы можем представлять дифференцируемую функцию следующим об-
разом:
y =lnu, где u =cosx.
Поэтому, согласно правилу дифференцирования сложной функции (см. теор. 98,
стр. 208), производная сложной функции y имеет следующий вид:
y
=
1
u
· u
, где u =cosx.
Подставим вместо u выражение этой функции через независимую переменную x,
после чего вычислим производную элементарной функции u(x)=cosx, просто
воспользовавшись таблицей производных (теор. 96, стр. 206):
y
=
1
cos x
· (cos x)
=
1
cos x
· (−sin x)=−ctg x.
Пример 149 Вычислим производную следующей функции: y =
√
x
2
+ x +1.
Данная функция является сложной, и мы можем трактовать ее следующим об-
разом:
y =
√
u, где u = x
2
+ x +1.
Действуем по правилу дифференцирования сложной функции (теор. 98, стр. 208):
y
=
1
2
√
u
· u
, где u = x
2
+ x +1.
Далее вычисляем производную функции u(x)=x
2
+ x +1, пользуясь правилом
дифференцирования суммы (теор. 97, стр. 206) и таблицей производных (теор. 96,
стр. 206) для вычисления производных каждого слагаемого:
y
=
1
2
√
x
2
+ x +1
· (x
2
+ x +1)
=
1
2
√
x
2
+ x +1
· (2x +1)=
2x +1
2
√
x
2
+ x +1
Возможны более сложные ситуации. Например, когда функция связана с неза-
висимой переменной не через одну, а через несколько промежуточных функций.
Принцип вычисления производной такой функции остается тем же. Продемон-
стрируем это на примере.
Пример 150 Пусть требуется продифференцировать функцию y =tg
√
ln x
.
Мы можем трактовать ее следующим образом:
y =tgu, где u =
√
ln x.
По правилу дифференцирования сложной функции (теор. 98, стр. 208), пользуясь
также таблицей производных элементарных функций (теор. 96, стр. 206), получим
следующее:
y
=
1
cos
2
u
· u
, где u =
√
ln x.
Подставим вместо функции u(x) ее выражение через независимую переменную:
u =
√
ln x . В результате, дифференцирование исходной сложной функции мы
свели дифференцированию другой функции (u =
√
ln x ), которая устроена проще
исходной.
y
=
1
cos
2
√
ln x
· (
√
ln x )
.
Выражение, стоящее в скобках, которое нам остается продифференцировать, сно-
ва является сложной функцией
u =
√
v, где v =lnx,

210 Приложение C. Функции и графики
к которой мы снова можем применить правило дифференцирования сложной
функции (теор. 98, стр. 208):
u
=
1
2
√
v
· v
, где v =lnx.
Таким образом, возвращаясь к вычислению исходной производной y
,мыможем
записать для нее следующее выражение:
y
=
1
cos
2
√
ln x
· (
√
ln x )
=
1
cos
2
√
ln x
·
1
2
√
ln x
· (ln x)
.
Теперь для получения результата нам остается продифференцировать ln x.Вос-
пользуемся таблицей производных (теор. 96, стр. 206), так как (ln x)
—этоуже
табличная производная.
y
=
1
cos
2
√
ln x
·(
√
ln x )
=
1
cos
2
√
ln x
·
1
2
√
ln x
·(ln x)
=
1
cos
2
√
ln x
·
1
2
√
ln x
·
1
x
.
Итак, окончательное выражение для производной таково:
y
=
1
2 x
√
ln x cos
2
√
ln x
.
Таким образом, применяя правило дифференцирования сложной функции нуж-
ное число раз, мы на каждом звене выкладки упрощаем вычисления и сводим, в
конечном счете, вычисления к какой-либо табличной производной.
Заметим, что в приведенных примерах на вычисление производных сложных
функций мы вводили вспомогательные обозначания для промежуточных функ-
ций. Следует иметь ввиду, что делать этого в реальных выкладках не следует.
Наоборот, нужно стремиться к тому, чтобы все расписанные нами выше очень
подробно рассуждения проводились бы вами в уме.
Например, в реальных (а не в учебных) условиях все решение примера 150 — это
одна строчка:
y
=
1
cos
2
√
ln x
·(
√
ln x )
=
1
cos
2
√
ln x
·
1
2
√
ln x
·(ln x)
=
1
cos
2
√
ln x
·
1
2
√
ln x
·
1
x
.
Все остальные рассуждения приведены для разъяснений по поводу производимых
действий.
Рассмотрим (уже не так подробно) еще несколько примеров.
Пример 151 Продифференцировать функцию y =sin2x · cos 3x.
Здесь функция является произведением двух функций, каждая из которых яв-
ляется сложной (так как, например, в первом случае элементарная функция sin
применяется не к независимой переменной x, а к выражению, зависящему от x,
именно: к 2x).
Поэтому прежде всего мы применяем правило дифференцирования произведения
(теор. 97, стр. 206) для того, чтобы свести вычисления к дифференцированию
множителей:
y
=(sin2x)
· cos 3x +sin2x · (cos 3x)
.
Появившиеся в правой части две производные мы можем взять по правилу диф-
ференцирования сложной функции (теор. 98, стр. 208).
y
=(sin2x)
· cos 3x +sin2x · (cos 3x)
=
=cos2x · (2x)
· cos 3x +sin2x · (−sin 3x) ·(3x)
=
=2cos2x cos 3x − 3sin2x sin 3x.
