Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

2.3. Линейные операторы 61
стр. 60). Следовательно:
Q
x
(e
1
)= e
1
,
Q
y
(e
2
)=−e
2
;
откуда Matr
E
(Q
x
)=
10
0 −1
.
Аналогично получается утверждение для симметрии Q
y
относительно вер-
тикальной оси (см. рис. 2.9, стр. 60).
Теорема 29 (матрица оператора масштабирования) В ортонормиро-
ванном базисе e
1
,e
2
матрица оператора S
k
1
,k
2
масштабированния плоскости
π с коэффициентами k
1
по горизонтали и k
2
по вертикали имеет вид:
Matr
E
(S
k
1
,k
2
)=
k
1
0
0 k
2
.
Доказательство Пусть на плоскости π фиксирован ортонормированный
базис e
1
,e
2
.
Под действием оператора масштабирования S
k
1
,k
2
единичный квадрат пе-
реходит в прямоугольник со сторонами k
1
, k
2
. При этом, так как вектор e
1
лежит на горизонтальной оси, он просто растягивается в k
1
раз, то есть —
переходит в вектор k
1
· e
1
(см. рис. 2.10, стр. 61). Аналогично — вектор e
2
переходит в вектор k
2
· e
2
. Следовательно:
S
k
1
,k
2
(e
1
)=k
1
· e
1
,
S
k
1
,k
2
(e
2
)=k
2
· e
2
;
откуда Matr
E
(S
k
1
,k
2
)=
k
1
0
0 k
2
.
0
e
1
e
2
S
k
1
,k
2
(e
2
)
S
k
1
,k
2
(e
1
)
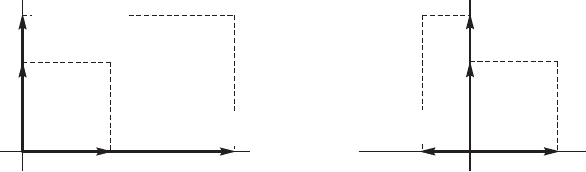
(a) Оба коэффициента масштабирова-
ния положительны.
0
e
1
e
2
S
k
1
,k
2
(e
2
)
S
k
1
,k
2
(e
1
)
(b) Коэффициент горизонтпльного
масштабирования отрицателен.
Рис. 2.10: Действие операторов масштабирования на базисные векторы.
Пример 47 На плоскости π фиксирован ортонормированный базис e
1
,e
2
.Вы-
числить координаты вектора, в который перейдет вектор x =(1, 1) под действием
оператора, сначала симметрично отражающего плоскость относительно горизон-
тальной оси, а затем — поворачивающего ее на угол π/4.
Интересующий нас оператор η — это произведение операторов Q
x
отражения от-
носительно горизонтальной оси и R
π/4
поворота на угол π/4:
η = R
π/4
Q
x
.

62 Глава 2. Линейная алгебра
Отметим, что в силу некоммутативности алгебры линейных операторов (см. при-
мер 41, стр. 53), произведение следует брать именно в этом порядке (справа на-
лево: сначала на аргумент действует отражение, а уже потом — поворот).
Далее мы должны перевести оператор η в матричную форму. В силу теоремы о
матрице произведения линейных операторов (см. теор. 24, стр. 57), матрица опе-
ратора η — это произведение двух матриц: матрицы оператора отражения и мат-
рицы оператора поворота (произведение опять-таки берется в соответствующем
порядке, а не иначе). Мы можем воспользоваться тем, что матрицы множителей
нам известны (см. тер. 28, стр. 60 и теор. 27, стр. 59):
Matr
E
(η)=Matr
E
(R
π/4
)Matr
E
(Q
x
)=
cos π/4 −sin π/4
sin π/4cosπ/4
10
0 −1
=
=
1/
√
2 −1/
√
2
1/
√
21/
√
2
10
0 −1
=
1/
√
21/
√
2
1/
√
2 −1/
√
2
.
Теперь — воспользуемся теоремой о действии линейного оператора на вектор в
матричной форме (см. теор. 21, стр. 56) и получим ответ:
η(x)=
1/
√
21/
√
2
1/
√
2 −1/
√
2
1
1
=
2/
√
2
0
.
Глава 3
Проективные операторы
Выше мы убедились, что большинство преобразований плоскости реализу-
ются в виде линейных операторов, которые, в свою очередь, могут быть
описаны при помощи матриц при условии, что на плоскости фиксирован
некий базис (см. теор. 27, стр. 59, теор. 28, стр. 60 и теор. 29, стр. 61).
Следовательно, для хранения плоского преобразования в графической си-
стеме ей достаточно передать двумерный массив чисел длины 2. Кроме то-
го, действие плоского преобразования, являющегося линейным оператором,
сводится к матричному умножению (см. теор. 21, стр. 56), которое не тре-
бует от графической системы ничего, кроме сложения и умножения чисел.
Процессор современного компьютера обладает очень высоким быстродей-
ствием, и выполнение таких операций с огромной скоростью позволяет вы-
полнять линейные преобразования графической сцены в режиме реального
времени.
Все это вселяет в нас сдержанный
P
2
R
3
z
x
y
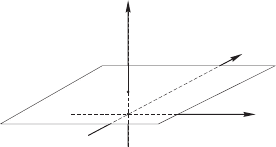
Рис. 3.1: Проективная плоскость P
2
,
вложенная в объемлющее трехмерное
пространство R
3
.
оптимизм.
Однако такое важное преобразова-
ние плоскости, как ее сдвиг (с точ-
ки зрения компьютерной графики
оно означает смещение объекта от-
носительно камеры или наоборот:
смещение камеры относительно гра-
фической сцены), не является ли-
ненйным оператором (см. пример 33,
стр. 48) и, следовательно, не может
быть представлено в матричной фор-
ме.
В настоящей главе мы преодолеем это препятствие путем перехода от век-
торных пространств к проективным, в частности — от плоскости, как дву-
мерного векторного пространства, к плоскости, как к двумерному проек-
тивному пространству (см. раздел 3.1, стр. 64).
Практичекские упражнения, относящиеся к данной теме, представлены в
приложениях (см. приложение B.3, стр. 198). Кроме того, как основной
63

64 Глава 3. Проективные операторы
практический результат первой части книги, мы подробно рассматриваем
один из алгоритмов покадровой 2d-анимации с геометрической и аналити-
ческой точек зрения (см. раздел 3.3, стр. 71).
3.1 Проективная плоскость
С геометрической точки зрения проективная плоскость ничем не отличает-
ся от обычной. Другое дело, что плоскость, рассматриваемая с проективной
точки зрения, позволяет аналитически раелизовать сразу две важнейшие
идеи:
• во-первых мы сможем отличать точки плоскости от векторов плоско-
сти (заметим, что в пределах линейной алгебры это одно и то же),
• и во-вторых мы сможем в единой матричной форме реализовать все
линейные плоские преобразования плюс смещение.
Определение 31 (проективная плоскость) Пусть в трехмерном физи-
ческом пространстве R
3
фиксирован ортонормированный базис e
1
,e
2
,e
3
.
Более того, будем считать, что на этом базисе в R
3
построена координат-
ная система с осями Ox, Oy, Oz. Проведем в R
3
плоскость, проходящую
через точку (0, 0, 1) параллельно плоскости xOy. Именно эта плоскость
1
,
которую мы будем обозначать P
2
, называется проективной плоскостью.
Итак, проективная плоскость P
2
получается из обыкновенной плоскости
π пустем вложения ее в объемлющее трехмерное векторное пространство.
Рассуждая аналогично, мы можем вложить трехмерное физическое про-
странство R
3
в объемлющее четырехмерное пространство и получить тем
самым проективное физическое пространство и т. д. Такой способ посто-
роения проективных пространств приводит к следующей теореме, которая
настолько очевидна (это, по сути, перефразировка определения), что мы
примем ее без формального доказательства.
Теорема 30 (проективные координаты) Каждая точка A проективной
плоскости P
2
обладает координатами вида (α
1
,α
2
, 1), а каждый вектор v
проективной плоскости P
2
обладает координатами вида (β
1
,β
2
, 0). Такие
координаты называются проективными координатами соответственно точ-
ки и вектора.
Таким образом, каждая точка проективной плоскости обладает одной “лиш-
ней” координатой: последнее, третье место всегда занимает 1, и каждый век-
тор проективной плоскости также обладает одной “лишней” координатой:
третье место всегда занимает 0.
Это утверждение, очевидно, остается справедливым и для проективных
пространств любой размерности: любая проективная точка в качестве своей
последней координаты имеет 1, и каждый проективный вектор в качестве
последней координаты имеет 0.
1
Строго говоря, данное нами определение является лишь одной из возможных реали-
заций проективной плоскости. Для решения задач, которые нас интересуют этого вполне
достаточно.
3.2. Проективные операторы 65
3.2 Проективные операторы
Здесь мы предъявим способ реализации всевозможных преобразований про-
ективной плоскости в виде матриц 3 × 3.
Ключевым результатом этого раздела является теорема о проективности
полскопараллельного смещения (см. теор. 35, стр. 68). Совместно с мат-
ричной реализацией поворотов, симметрий и масштабировний полученной
выше, этот результат даст метод аналитического описания любого преоб-
разования плоскости.
Определение 32 (проективный оператор) Пусть P
2
— это проектив-
ная плоскость, вложенная в объемлющее трехмерное векторное простран-
ство R
3
. Далее, пусть в объемлющем пространстве действует линейный опе-
ратор ϕ:
ϕ : R
3
−→ R
3
.
Он называется проективным оператором, действующим в проективной плос-
кости P
2
, если под его действием проективная плоскость P
2
переходит в
себя:
ϕ : P
2
−→ P
2
.
Пример 48 Пусть P
2
— проективная плоскость, вложенная в объемлющее трех-
мерное пространство R
3
. Далее, пусть в R
3
фиксирован ортонормированный ба-
зис e
1
,e
2
,e
3
, на котором построена координатная система. Рассмотрим поворот
R
α
объемлющего пространства относительно оси Oz на угол α:
R
α
: R
3
−→ R
3
.
Он, очевидно, является линейным оператором. При этом под его действием про-
ективная плоскость P
2
переходит в себя:
R
α
: P
2
−→ P
2
.
Таким образом, мы получаем проективный оператор, действующий в проективной
плоскости P
2
, поворотом относительно начала координат на угол α.
С другой стороны, если мы рассмотрим поворот объемлющего пространства R
3
на угол α относительно любой другой прямой, например, относительно оси Ox,то
под действием такого преобразования плоскость P
2
перейдет в какую-то другую
плоскость, но не в себя. Следовательно, несмотря на то, что этот поворот тоже
является линейным оператором, действующим в объемлющем пространстве, он не
является проективным оператором, действующим в проективной плоскости P
2
.
Определение 33 (матрица проективного оператора) Пусть на проек-
тивной плоскости P
2
действует проективный оператор ϕ:
ϕ : P
2
−→ P
2
.
Его матрицей называется матрица соответствующего линейного оператора,
действующего в объемлющем векторном пространстве:
ϕ : R
3
−→ R
3
.
66 Глава 3. Проективные операторы
Пример 49 Рассмотрим поворот R
α
проективной плоскости P
2
на угол α отно-
сительно начала координат. В объемлющем пространстве R
3
ему соответствует
поворот на угол α относительно вертикальной координатной оси Oz. Матрицу
этого оператора нетрудно выписать. Так как в объемлющем пространстве фикси-
рован ортонормированный базис e
1
,e
2
,e
3
, то:
R
α
(e
1
)= cosα · e
1
+sinα ·e
2
+0·e
3
R
α
(e
2
)=−sin α · e
1
+cosα · e
2
+0·e
3
R
α
(e
3
)= 0·e
1
+0· e
2
+ e
3
Из этих разложений, пользуясь определением матрицы линейного оператора, по-
лучаем:
Matr
E
(R
α
)=
cos α −sin α 0
sin α cos α 0
001
.
Рассмотренный пример является частным случаем общей ситуации, кото-
рую мы изложим в виде следующей теоремы.
Теорема 31 (о матрице проективного оператора) Пусть на плоскости
π фиксирован ортонормированный базис e
1
,e
2
, и пусть она вложена как
проективная плоскость P
2
в объемлющее трехмерное пространство R
3
,в
котором фиксирован ортонормированный базис e
1
,e
2
,e
3
. Пусть на плоско-
сти π действует линейный оператор ϕ:
ϕ : π −→ π,
и пусть его матрица, выписанная в базисе e
1
,e
2
— это:
Matr
E
(ϕ)=
a
11
a
12
a
21
a
22
.
Тогда матрица соответствующего проективного оператора ϕ, действующего
на проективной плоскости
ϕ : P
2
−→ P
2
,
имеет следующий блочно-диагональный вид:
Matr
E
(ϕ)=
a
11
a
12
0
a
21
a
22
0
001
.
Доказательство По определению проективного оператора (см. опр. 32,
стр.65), линейный оператор, действующий в объемлющем пространстве, на
первые два базисных вектора e
1
и e
2
действует так же, как и на плоскости
π, а третий базисный вектор e
3
переводит в себя.
Подействуем на базисные векторы e
1
,e
2
плоскости π в матричной форме:
ϕ(e
1
)=
a
11
a
12
a
21
a
22
1
0
=
a
11
a
21
= a
11
e
1
+ a
21
e
2
,
ϕ(e
2
)=
a
11
a
12
a
21
a
22
0
1
=
a
12
a
22
= a
12
e
1
+ a
22
e
2
.
3.2. Проективные операторы 67
Следовательно, продолжая действие оператора на объемлющее простран-
ство, получим:
ϕ(e
1
)=a
11
e
1
+ a
21
e
2
+0· e
3
ϕ(e
2
)=a
12
e
1
+ a
22
e
2
+0· e
3
ϕ(e
3
)= 0· e
1
+0· e
2
+ e
3
Применим определение матрицы линейного оператора, выписывая коэффи-
циенты разложений по столбцам, и получим требуемое.
Теорема доказана.
Теперь, при помощи этой теоремы, мы можем накрыть очень широкий блок
проективных операторов, пользуясь теми результатами, которые получили
выше.
Теорема 32 (матрицы проективных поворотов) Матрицы проектив-
ных поворотов R
α
проективной плоскости P
2
на угол α относительно нача-
ла координат имеют вид:
Matr
E
(R
α
)=
cos α −sin α 0
sin α cos α 0
001
.
Теорема 33 (матрицы проективных симметрий) Матрицы проектив-
ных симметрий Q
x
и Q
y
проективной плоскости P
2
относительно осей Ox
и Oy соответственно имеют вид:
Matr
E
(Q
x
)=
100
0 −10
001
, Matr
E
(Q
y
)=
−100
010
001
.
Теорема 34 (матрицы проективных масштабирований) Матрицы
проективных масштабирований S
k
1
,k
2
проективной плоскости P
2
относи-
тельно начала координат с коэффициентом k
1
по горизонтали и с коэффи-
циентом k
2
по вертикали имеют вид:
Matr
E
(S
k
1
,k
2
)=
k
1
00
0 k
2
0
001
.
Все эти утверждения напрямую получаются из только что доказанной тео-
ремы (см. теор. 31, стр. 66) с учетом результатов, полученных ранее относи-
тельно матриц операторов поворота (см. теор. 27, стр. 59), симметрий (см.
теор. 28, стр. 60) и масштабирования (см. теор. 29, стр. 61). Их доказатель-
ства мы опускаем (они тривиальны).
Пример 50 Треугольник с вершинами A(1, −1), B(2, 3), C(−2, 5) равномерно
двукратно масштабируется относительно начала координат. Вычислить коорди-
наты результирующего треугольника A
B
C
.
Перейдем к проективным координатам A =(1, −1, 1), B =(2, 3, 1), C =(−2, 5, 1)
и воспользуемся матричным представлением проективного масштабирования:
A
= S
2,2
(A)=
200
020
001
1
−1
1
=
2
−2
1
.
68 Глава 3. Проективные операторы
Аналогично — B
=(4, 6, 1), C
=(−4, 10, 1). Следовательно, возвращаясь к де-
картовым координатам, имеем: A
(2, −2), B
(4, 6), C
(−4, 10).
Пример 51 Треугольник с вершинами A(2, 1), B(2, 3), C(4, 1) поворачивается на
угол π/2 относительно начала координат. Вычислить координаты результирую-
щего треугольника A
B
C
.
Перейдем к проективным координатам A =(2, 1, 1), B =(2, 3, 1), C =(4, 1, 1) и
воспользуемся матричным представлением проективного вращения:
A
= R
π/2
(A)=
0 −10
100
001
2
1
1
=
−1
2
1
.
Аналогично — B
=(−3, 2, 1), C
=(−1, 4, 1). Следовательно, возвращаясь к де-
картовым координатам, имеем: A
(−1, 2), B
(−3, 2), C
(−1, 4).
Пример 52 Треугольник с вершинами A(2, 2), B(3, 4), C(3, 2) симметрично от-
ражается относительно вертикальной оси Oy. Вычислить координаты результи-
рующего треугольника A
B
C
.
Перейдем к проективным координатам A =(2, 2, 1), B =(3, 4, 1), C =(3, 2, 1) и
воспользуемся матричным представлением проективной симметрии:
A
= Q
y
(A)=
−100
010
001
2
2
1
=
−2
2
1
.
Аналогично — B
=(−3, 4, 1), C
=(−3, 2, 1). Следовательно, возвращаясь к де-
картовым координатам, имеем: A
(−2, 2), B
(−3, 4), C
(−3, 2).
Однако полученные матричные выражения для основных линейных преоб-
разований плоскости не привнесли ничего нового в уже имевшийся у нас
инструментарий работы с плоскостью. Те же самые действия мы могли бы
выполнять и в декартовых координатах. Принципиально новым же являет-
ся тот факт, что смещение плоскости мы можем реализовать в виде проек-
тивного оператора и, следовательно, в виде матрицы 3 × 3. Этот результат
дает нам следующая теорема.
Теорема 35 (проективность смещения) Пусть преобразование T
a
дей-
ствует на плоскости π смещением на вектор a =(a
1
,a
2
) (предполагается,
что на плоскости фиксирован ортонормированный базис e
1
,e
2
). Тогда T
a
является проективным оператором, действующим на проективной плоско-
сти P
2
, причем он обладает следующей матрицей:
Matr
E
(T
a
)=
10a
1
01a
2
00 1
.
Доказательство
Рассмотрим в объемлющем пространстве R
3
преобразование Sw
a
скоса на
вектор a, действующее на базисные векторы следующим образом:
Sw
a
(e
1
)=e
1
,Sw
a
(e
2
)=e
2
,
Sw
a
(e
3
)=e
3
+ a.
3.2. Проективные операторы 69
Отметим некоторые свойства этого преобразования.
Во-первых, оно, со всей очевидностью, является линейным. Во-вторых, оно
переводит проективную плоскость P
2
в себя, причем в пределах P
2
скос
объемлющего пространства действует именно как смещение на вектор a.
Действительно, так как вектор a ле-
P
2
R
3
z
e
3
a
Sw
a
(e
3
)
x
y
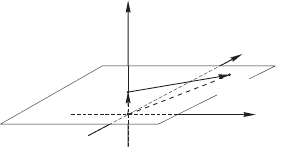
Рис. 3.2: Скос, действующий в P
2
как
смещение.
жит в горизонтальной координат-
ной плоскости, прибавление его к
любому вектору из R
3
не изменяет
его третьей координаты. В частно-
сти, любой вектор, лежащий в P
2
,
остается в ее пределах.
Следовательно, согласно определе-
нию (см. опр. 32, стр. 65), смеще-
ние T
a
проективной плоскости P
2
на вектор a является проективным
оператором.
Далее, мы можем выписать матрицу скоса:
Sw
a
(e
1
)= 1· e
1
+0· e
2
+0· e
3
,
Sw
a
(e
2
)= 0· e
1
+1· e
2
+0· e
3
,
Sw
a
(e
3
)=a
1
· e
1
+ a
2
· e
2
+1· e
3
.
Выписывая коэффициенты разложений по столбцам, получим требуемое:
Matr
E
(T
a
)=
10a
1
01a
2
00 1
.
Теорема доказана.
Теперь спектр наших возможностей преобразовать плоскость существенно
пополнился, можно сказать, что теперь он стал окончательным: помимо
прямых смещений плоскости, мы можем теперь выполнять масштабирова-
ния и повороты относительно произвольной точки плоскости, а также —
симметрии относительно произвольных прямых. Проиллюстрируем это на
примерах.
Пример 53 Треугольник с вершинами A(2, 1), B(2, 2), C(4, 2) вращается относи-
тельно точки G(1, 3) на угол π/2 (см. рис. 3.3, стр. 70). Найти координаты вершин
результирующего треугольника A
B
C
.
Поворот плоскости как линейный оператор возможен только относительно нача-
ла координат. Поэтому, для того, чтобы получить нужное нам преобразование
η в матричной форме, необходимо сначала сместить центр вращения G(1, 3) на
вектор b =(−1, −3) (то есть — выполнить трансляцию T
b
), затем произвести по-
ворот плоскости R
π/2
на угол π/2 и после этого выполнить обратное смещение:

70 Глава 3. Проективные операторы
x
y
G
0
π/2
(a) Поворот относительно произ-
вольной точки.
x
y
0
l
(b) Симметрия относительно про-
извольной (горизонтальной) оси.
Рис. 3.3: Примеры линейных преобразования плоскости, использующих сме-
щения.
трансляцию T
−b
на вектор −b =(1, 3).
η = T
−b
R
π/2
T
b
=
101
013
001
cos π/2 −sin π/20
sin π/2cosπ/20
001
10−1
01−3
00 1
=
=
101
013
001
0 −10
100
001
10−1
01−3
00 1
=
=
0 −14
102
001
.
Теперь можно вычислить координаты результирующего треугольника просто при
помощи матричного умножения. Для этого — переходим к проективным коорди-
натам:
A
= η (A)=
0 −14
102
001
2
1
1
=
3
4
1
таким образом A
(3, 4).
B
= η (B)=
0 −14
102
001
2
2
1
=
2
4
1
и, значит, B
(2, 4).
C
= η (C)=
0 −14
102
001
4
2
1
=
2
6
1
следовательно, C
(2, 6).
Пример 54 Треугольник с вершинами A(2, 3), B(2, 5), C(4, 4) симметрично от-
ражается относительно прямой l : y =2(см. рис. 3.3, стр. 70). Найти координаты
вершин результирующего треугольника A
B
C
.
Выше мы отнесли к основным плоским преобразованиям симметричные отраже-
ния Q
x
, Q
y
плоскости относительно координатных осей. Поэтому для реализации
