Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.

2.2. Векторные пространства 41
2. Плоскость π, помимо несобственных подпространств, обладает еще и соб-
ственными. Опишем их. Подмножеством плоскости, являющимся вектор-
ным пространством может служить только какая-нибудь прямая (см. заме-
чание к примеру 11, стр.28). Однако, если прямая не содержит отмеченную
точку (начало координат), то легко можно показать, что такая прямая не
является подпространством.
Действительно: пусть прямая m не проходит через ноль. Тогда, если v ∈ m,
то, в силу устойчивости относительно скалярного кратного, αv ∈ m для
любого значения коэффициента α. В частности, если α =0,то0v ∈ m,то
есть — 0 ∈ m. Но это противоречит предположению, что m не проходит
через нулевую точку.
Итак, собственными подпространствами плоскости служат прямые, прохо-
дящие через начало координат. Отметим здесь же, что плоскость двумерна,
а ее собственные подпространства — одномерны.
3. Рассуждая аналогично, можно убедиться, что физическое пространство R
3
,
помимо несобственных подпространств, содержит еще и собственные под-
пространства двух типов: это прямые, проходящие через начало координат,
и плоскости, проходящие через начало координат.
Заметим, что в тот момент, когда физическое пространство трехмерно, его
собственные подпространства либо одномерны (прямые), либо двумерны
(плоскости).
Пример 26 Покажем, что множество M диагональных матриц второго порядка
образует векторное подпространство в полной матричной алгебре второго порядка
Matr
2
. В качестве образующих множества M можно выбрать матрицы
E
11
=
10
00
,E
22
=
00
01
.
Действительно, тогда любая матрица A из M может быть представлена в виде
линейной комбинации матриц E
11
, E
22
:
A =
a 0
0 b
= a
10
00
+ b
00
01
,
причем это разложение единственно. Следовательно (см. опр. 17, стр. 36 и теор. 13,
стр. 37), матрицы E
11
, E
22
являются более, чем образующими можества V —это
его базис. Тем самым мы показали, что множество M является векторным подпро-
странством в Matr
2
, указали его базис и получили его размерность: dim M =2.
2.2.5 Замена базиса
Ранее мы указывали, что базис векторного пространства является инстру-
ментом, при помощи которого можно численно (то есть, в координатах)
описывать векторы векторного пространства.
Однако мы никогда не говорили, что базис можно выбрать единственным
способом. Более того, из определения (см. опр. 17, стр. 36) напрямую вы-
текает, что любое векторное пространство обладает бесконечным числом
различных базисов (вспомните, что даже на прямой, базис которой состоит
из единственного ненулевого вектора, этот вектор может быть любым, то
есть имеется бесконечное число способов выбрать базис на прямой).

42 Глава 2. Линейная алгебра
0
e
1
e
2
α
1
α
2
x
π
(a) Разложение вектора x по
базису E: x = α
1
· e
1
+ α
2
· e
2
.
0
f
1
f
2
β
1
β
2
x
π
(b) Разложение вектора x по
базису F : x = β
1
· f
1
+ β
2
· f
2
.
Рис. 2.3: Разложения вектора по разным базисам.
Вместе с тем, очевидно, что один и тот же вектор в различных базисах будет
описываться по-разному — он будет иметь разные координатные представ-
ления. То есть, набор координат, описывающий данный вектор, полностью
зависит от базиса, в котором эти координаты вычисляются (см. рис. 2.3,
стр. 42).
В этом разделе мы получим формулы, связывающие координатные пред-
ставления вектора в различных базисах.
Определение 21 (матрица перехода) Пусть V —векторное простран-
ство, в котором фиксированы два базиса: e
1
,...,e
n
и f
1
,...,f
n
. Векторы
f
1
,...,f
n
, как векторы векторного пространства V , раскладываются по ба-
зису e
1
,...,e
n
, причем однозначно:
f
1
= a
11
e
1
+ a
12
e
2
+ ··· + a
1n
e
n
f
2
= a
21
e
1
+ a
22
e
2
+ ··· + a
2n
e
n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
f
n
= a
n1
e
1
+ a
n2
e
2
+ ··· + a
nn
e
n
Матрицей A перехода от базиса e
1
,...,e
n
к базису f
1
,...,f
n
называется
матрица коэффициентов разложений, выписанных по столбцам:
A =
a
11
a
21
··· a
n1
a
12
a
22
··· a
n2
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
··· a
nn
.
Теорема 15 (о замене базиса) Пусть V — векторное пространство, снаб-
женное базисами e
1
,...,e
n
и f
1
,...,f
n
.Тогда
x
F
= A
−1
x
E
,
где x
F
— координатное представление вектора x в базисе f
1
,...,f
n
, x
E
—
координатное представление вектора x в базисе e
1
,...,e
n
,аA — матрица
перехода от базиса E к базису F .
Доказательство Покажем, что справедливо соотношение x
E
= Ax
F
.Пусть
нам известны разложения вектора x по базисам e
1
,...,e
n
и f
1
,...,f
n
:
x
E
=(α
1
, ... , α
n
)=α
1
e
1
+ ···+ α
n
e
n
,
x
F
=(β
1
, ... , β
n
)=β
1
f
1
+ ···+ β
n
f
n
.
2.2. Векторные пространства 43
Разложим векторы базиса f
1
,...,f
n
по векторам базиса e
1
,...,e
n
:
f
1
= a
11
e
1
+ a
12
e
2
+ ··· + a
1n
e
n
f
2
= a
21
e
1
+ a
22
e
2
+ ··· + a
2n
e
n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
f
n
= a
n1
e
1
+ a
n2
e
2
+ ··· + a
nn
e
n
Тогда мы можем преобразовать разложение вектора x по базису f
1
,...,f
n
к разложению по базису e
1
,...,e
n
:
x
F
=(β
1
, ... , β
n
)=β
1
f
1
+ ···+ β
n
f
n
=
= β
1
(a
11
e
1
+ ···+ a
1n
e
n
)+···+ β
n
(a
n1
e
1
+ ···+ a
nn
e
n
)=
=(β
1
a
11
+ ···+ β
n
a
n1
)e
1
+ ···+(β
1
a
1n
+ ···+ β
n
a
nn
)e
n
=
=(α
1
, ... , α
n
)=x
E
.
Приравнивая коэффициенты при базисных векторах e
1
,...,e
n
вразложе-
нии вектора x и координаты α
1
,...,α
n
вектора x в базисе e
1
,...,e
n
,полу-
чим систему:
α
1
= β
1
a
11
+ β
2
a
21
+ ··· + β
n
a
n1
,
α
2
= β
1
a
12
+ β
2
a
22
+ ··· + β
n
a
n2
,
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
α
n
= β
1
a
1n
+ β
2
a
2n
+ ··· + β
n
a
nn
;
которая преобразуется к матричному виду:
α
1
α
2
.
.
.
α
n
=
a
11
a
21
··· a
n1
a
12
a
22
··· a
n2
.
.
.
.
.
.
.
.
.
.
.
.
a
1n
a
2n
··· a
nn
β
1
β
2
.
.
.
β
n
.
Тем самым, нами доказано соотношение x
E
= Ax
F
. Умножая его слева на
A
−1
, получим требуемое: x
F
= A
−1
x
E
.
Теорема доказана.
Пример 27 Пусть на плоскости π фиксирован базис e
1
,e
2
. И пусть на ней выбран
еще один базис, f
1
,f
2
:
f
1
= e
1
+ e
2
,
f
2
= −e
1
.
Допустим, нам известны координаты вектора x в базисе e
1
,e
2
: x
E
=(−1, 1).Тре-
буется вычислить координаты вектора x в базисе f
1
,f
2
.
Воспользуемся теоремой о замене базиса (см. теор. 15, стр. 42):
x
F
= A
−1
x
E
,
где A — матрица перехода от базиса e
1
,e
2
к базису f
1
,f
2
. В нашем случае
A =
1 −1
10
.

44 Глава 2. Линейная алгебра
Прежде всего, необходимо вычислить матрицу A
−1
, обратную к матрице перехо-
да. Воспользуемся для этого методом Гаусса:
1 −1
10
10
01
−I
∼
1 −1
01
10
−11
+II
∼
10
01
01
−11
.
Следовательно,
x
F
=
01
−11
−1
1
=
1
2
.
2.3 Линейные операторы
Линейные операторы представляют собой очень важный класс преобразо-
ваний, действующих в векторных пространствах. Они привлекательны уже
хотя бы потому, что могут быть реализованы в виде матриц (см. опр. 30,
стр. 55), а их действие — в виде операции матричного умножения (см.
теор. 21, стр. 56).
В этом разделе мы установим взаимно-однозначное соответствие (так на-
зываемый изоморфизм алгебр) между алгеброй линейных операторов, дей-
ствующих в векторном пространстве и полной матричной алгеброй соот-
ветствующего порядка (см. теор. 25, стр. 58).
В результате будет получен исключительно удобный (ведь матричное умно-
жение сводится к сложению и умножению чисел) вычислительный меха-
низм для преобразований векторных пространств (в частности, плоскости,
как двумерного векторного пространства).
Большинство разумных преобразований плоскости (повороты, масштабиро-
вания, отражения и т.д.) являются линейными (см. раздел 2.3.1, стр. 44)
16
,
и, в заключение этого раздела, мы вычислим их матрицы (см. раздел 2.3.5,
ср. 59).
Практические примеры, относящиеся к этому разделу, представлены в при-
ложениях (см. приложение B.2, стр. 193).
2.3.1 Определения и примеры
Определение 22 (линейный оператор) Пусть в векторном простран-
стве V действует проебразование ϕ:
ϕ : V −→ V.
Оно называется линейным оператором, если выполняются следующие два
условия.
1. Под действием преобразования ϕ сумма векторов u и v переходит в
сумму их образов ϕ(u) и ϕ(v):
ϕ(u + v)=ϕ(u)+ϕ(v) ∀ u, v ∈ V.
16
Исключение составляет только смещение плоскости (см. пример 33, стр. 48), однако
мы преодолеем эту трудность в следующей главе путем перехода к проективным про-
странствам и проективным операторам (см. главу 3, стр. 63).

2.3. Линейные операторы 45
2. Под действием преобразования ϕ скалярное кратное αu вектора u пе-
реходит в скалярное кратное его образа ϕ(u) (другими словами — по-
стоянный множитель можно выносить из-под знака линейного опера-
тора):
ϕ(αu)=αϕ(u) ∀ u ∈ V, α∈ R.
Пример 28 (тривиальные линейные операторы) В любом векторном про-
странстве V действуют два линейных оператора, называемых тривиальными: это
нулевой оператор, под действием которого любой вектор v векторного простран-
ства V переходит в ноль, и единичный оператор, под действием которого любой
вектор v векторного пространства V переходит в себя.
v
e
1
e
2
0
p
x
(v)
(a) Проектор p
x
на гори-
зонтальную ось.
u
p
x
(v)
p
x
(u)
0
v
u + v
p
x
(u + v)
(b) Действие проектора p
x
на сумму векторов.
v
αv
p
x
(v)
p
x
(αv)
0
(c) Действие проектора p
x
на скалярное кратное век-
тора.
Рис. 2.4: Проектор на горизонтальную ось является линейным оператором,
действующим на плоскости.
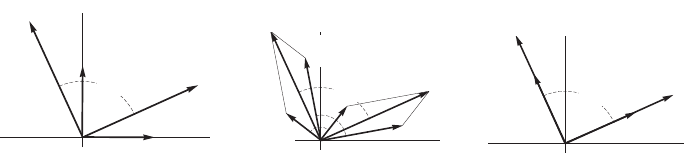
Пример 29 (проекторы) Пусть на плоскости π фиксирован ортонормирован-
ный
17
базис e
1
,e
2
. Будем считать также, что вдоль базисных векторов направлены
координатные оси Ox и Oy.Пустьp
x
действует на плоскости π
p
x
: π −→ π,
следующим образом: под его действием любой вектор плоскости π переходит в
проекцию на горизонтальную ось Ox (см. рис. 2.4, стр.45). Это преобразование
называется проектором плоскости на горизонтальную ось.
Оно является линейным оператором. Действительно, в силу известных геометри-
ческих соотношений, проекция суммы равна сумме проекций, а проекция скаляр-
ного кратного — скалярному кратному проекций (см. рис. 2.4, стр.45):
p
x
(u + v)=p
x
(u)+p
x
(v) ∀ u, v ∈ V,
p
x
(αu)=αp
x
(u) ∀ u ∈ V, α∈ R.
Поэтому, в силу данного выше определения (см. опр. 22, стр. 44), проектор на
горизонтальную ось является линейным оператором.
Аналогично — проектор p
y
, действующий проекцией на вертикальную ось, явля-
ется линейным оператором. Более того, мы могли бы не требовать изначально
ортогональности базиса e
1
,e
2
и соответствующей системы координат. Неортого-
нальное проецирование также является линейным оператором.
17
Ортонормированным называется базис, состоящий из взаимноперпендикулярных
векторов единичной длины.
46 Глава 2. Линейная алгебра
Обобщая этот пример на трехмерный случай физического пространства, можно
утверждать, что проекторы p
x
, p
y
, p
z
, действующие в физическом пространстве
проекциями вдоль координатных осей, а также проекторы p
xOy
, p
xOz
, p
yOz
,дей-
ствующие в физическом пространстве проекциями вдоль координатных плоско-
стей, являются линейными операторами.
v
e
1
e
2
0
α
R
α
(v)
(a) Поворот R
α
плоскости
на угол α.
u
R
α
(v)
R
α
(u)
0
α
v
u + v
R
α
(u + v)
(b) Действие поворота R
α
на сумму векторов.
R
α
(v)
0
α
v
kv
R
α
(kv)
(c) Действие поворота R
α
на скалярное кратное векто-
ра.
Рис. 2.5: Поворот на угол α плоскости относительно начала координат яв-
ляется линейным оператором, действующим на плоскости.
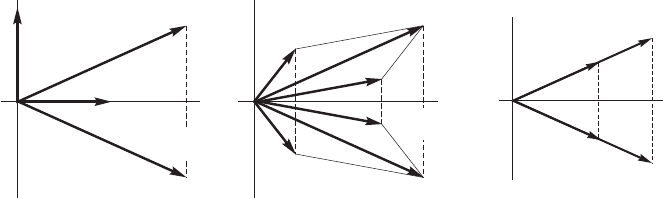
Пример 30 (повороты) Пусть на плоскости π фиксирован ортонормирован-
ный базис e
1
,e
2
. Будем считать также, что вдоль базисных векторов направлены
координатные оси Ox и Oy. Пусть преобразование R
α
действует на плоскости π
R
α
: π −→ π
поворотом на угол α относительно начала координат (см. рис. 2.5, стр.46). Оно
также является линейным оператором.
Действительно, под действием поворота параллелограмм, построенный на век-
торах u и v, переходит в конгруэнтный параллелограмм (см. рис. 2.5, стр.46), а
значит,
R
α
(u + v)=R
α
(u)+R
α
(v) ∀ u, v ∈ V.
Кроме того, так как поворот сохраняет длины отрезков,
R
α
(βu)=βR
α
(u) ∀ u ∈ V, β ∈ R.
Следовательно, по определению (см. опр. 22, стр. 44), поворот на угол α плоскости
относительно начала координат является линейным оператором.
Заметим, что в этом случае требование ортогональности базиса и соответствую-
щей координатной системы является обязательным.
Мы можем обобщить этот пример на трехмерное физическое пространство. А
именно, поворот физического пространства на угол α относительно любой прямой
l, проходящей через начало координат, является линейным оператором.
Пример 31 (симметрии) Пусть на плоскости π фиксирован ортонормирован-
ный базис e
1
,e
2
. Будем считать также, что вдоль базисных векторов направлены
координатные оси Ox и Oy. Пусть преобразование Q
x
действует на плоскости π
Q
x
: π −→ π
2.3. Линейные операторы 47
v
e
1
e
2
0
Q
x
(v)
(a) Симметрия Q
x
отно-
сительно горизонтальной
оси.
u
0
v
u + v
Q
x
(u)
Q
x
(u + v)
Q
x
(v)
(b) Действие симметрии
Q
x
на сумму векторов.
v
αv
Q
x
(v)
Q
x
(αv)
0
(c) Действие симметрии
Q
x
на скалярное кратное
вектора.
Рис. 2.6: Симметрия относительно горизонтальной оси является линейным
оператором, действующим на плоскости.
симметричным отражением относительно горизонтальной оси. Это преобразова-
ние также является линейным оператором.
Действительно, под действием симметричного отражения параллелограмм, по-
строенный на векторах u и v, переходит в конгруэнтный параллелограмм, а зна-
чит,
Q
x
(u + v)=Q
x
(u)+Q
x
(v) ∀ u, v ∈ V.
Кроме того, так как симметрия сохраняет длины отрезков,
Q
x
(αu)=αQ
x
(u) ∀ u ∈ V, α∈ R.
Следовательно, по определению (см. опр. 22, стр. 44), симметричное отражение
плоскости относительно горизонтальной оси является линейным оператором.
Понятно, что симметричное отражение плоскости относительно вертикальной оси
точно так же является линейным оператором. Более того, отражения плоскости
относительно любой прямой, проходящей через начало координат, являются ли-
нейными операторами.
Обобщая эти примеры на трехмерный случай физического пространства R
3
, от-
метим, что отражения R
3
относительно прямых и плоскостей, проходящих через
начало координат, являются линейными операторами.
Пример 32 (масштабирования) Пусть на плоскости π фиксирован ортонор-
мированный базис e
1
, e
2
, вдоль векторов которого направлены координатные оси.
Пусть отображение S
k
1
,k
2
действует на плоскости
S
k
1
,k
2
: π −→ π
растяжением плоскости в k
1
раз вдоль горизонтальной оси и в k
2
раз вдоль вер-
тикальной оси. Это отображение также является линейным оператором.
Несложно обобщить этот пример на случай трехмерного физического простран-
ства:
S
k
1
,k
2
,k
3
: R
3
−→ R
3
.
Это масштабирование растягивает физическое пространство в k
1
раз вдоль оси
Ox,вk
2
раз вдоль оси Oy ивk
3
раз вдоль оси Oz.
48 Глава 2. Линейная алгебра
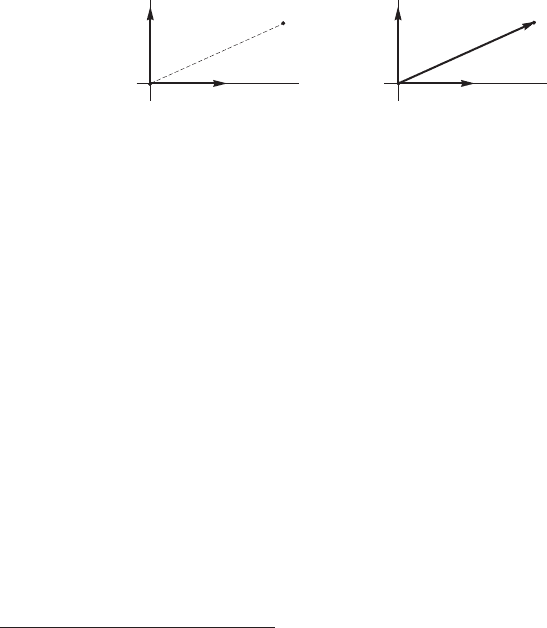
Пример 33 (смещение не является линейным оператором!) Вместе с тем,
такое важное преобразование плоскости, как смещение
18
T
a
плоскости π на вектор
a, не является линейным оператором.
Дело в том, что под действием линейного оператора нулевой вектор должен пе-
рейти в себя. Действительно, пусть ϕ — линейный оператор, действующий в век-
торном пространстве V .Тогда
ϕ(0) = ϕ(0v)=0ϕ(v)=0.
Под действием же смещения нулевой вектор переходит в вектор смещения a:
T
a
(0) = a.
Это обстоятельство приведет нас к необходимости организовывать так называет-
мые проективные пространства, вкладывая их специальным образом в объемлю-
щие векторные пространства (см. главу 3, стр. 63).
a
e
1
e
2
0
(a) Смещение T
a
плоско-
сти на вектор a.
a
e
1
e
2
0
T
a
(0)
(b) Действие смещения на
нулевой вектор.
Рис. 2.7: Смещение плоскости на вектор a не является линейным операто-
ром, так как под его действием нулевой вектор не переходит в себя.
2.3.2 Ядро и образ линейного оператора
Здесь мы приведем очень важное для дальнейших целей понятие невырож-
денного линейного оператора
19
.
Определение 23 (ядро линейного оператора) Пусть V — векторное про-
странство, ϕ — линейный оператор, действующий в V . Его ядром называ-
ется множество векторов векторного пространства V , переходящих под его
действием в ноль:
Ker ϕ = {v ∈ V | ϕ(v)=0}.
Ядро линейного оператора обозначается Ker от английского kernel — ядро.
18
С точки зрения графических систем, смещение означает смещение камеры относи-
тельно графической сцены или, что то же самое, смещение объекта относительно непо-
движной камеры.
19
Именно невырожденные преобразования плоскости представляют интерес с точки
зрения организации графических систем, так как под действием невырожденного линей-
ного оператора плоскость переходит в себя, а не коллапсирует к прямой или точке.
2.3. Линейные операторы 49
Определение 24 (образ линейного оператора) Пусть V — векторное
пространство, ϕ — линейный оператор, действующий в V . Его образом на-
зывается множество векторов векторного пространства V , в которые пере-
ходят все векторы векторного пространства V :
Im ϕ = {v ∈ V |∃v
∈ V,ϕ(v
)=v}.
Образ линейного оператора обозначается Im от английского image — образ.
Пример 34 (тривиальные операторы) Нетрудно понять, что, согласно дан-
ным определениям (см. опр. 23, стр. 48 и опр. 24, стр. 48), ядром нулевого опера-
тора, действующего в векторном пространстве V (см. пример 28, стр. 45) служит
все пространство V , а образом — единственный вектор: нулевой.
Рассматривая же единичный оператор из того же примера, приходим к выво-
ду, что ядром единичного оператора служит единственный вектор (а именно —
нулевой вектор), а образом единичного оператора служит все пространство.
Пример 35 (проекторы) Рассмотрим проекторы p
x
, p
y
, действующие на плос-
кости π (см. пример 29, стр. 45). В силу определений (см. опр. 23, стр. 48 и опр. 24,
стр. 48), ядром и образом оператора p
x
служат координатные оси:
Ker p
x
= Oy , Im p
x
= Ox .
Аналогично — для оператора p
y
:
Ker p
y
= Ox , Im p
y
= Oy .
Теорема 16 (о ядре и образе линейного оператора) Ядро и образ ли-
нейного оператора ϕ, действующего в векторного пространстве V , являются
векторными подпространствами в V .
Доказательство Начнем с ядра Ker ϕ. Нам нужно показать, что мно-
жество Ker ϕ устойчиво относительно двух операций: суммы и скалярного
кратного. Согласно определению векторного подпространства (см. опр. 19,
стр. 40) это будет означать, что Ker ϕ является векторным подпростран-
ством в V .Пустьu, v ∈ Ker ϕ.Тогда
ϕ(u + v)=ϕ(u)+ϕ(v)=0+0=0,
то есть u + v ∈ Ker ϕ, и устойчивость ядра относительно суммы доказа-
на. Несложно доказать и устойчивость относительно скалярного кратного.
Если u ∈ Ker ϕ,то
ϕ(αu)=αϕ(u)=α · 0=0,
следовательно, αu ∈ Ker ϕ, и ядро устойчиво относительно скалярного крат-
ного. Итак, ядро линейного оператора ϕ является векторным подпростран-
ством в пространстве V .
Далее, нас интересует образ оператора Im ϕ.Пустьu, v ∈ Im ϕ.Тогда,по
определению (см. опр. 24, стр. 48) существуют векторы u
,v
∈ V такие, что
ϕ(u
)=u, ϕ(v
)=v. Подействуем оператором ϕ на сумму векторов u
+ v
:
ϕ(u
+ v
)=ϕ(u
)+ϕ(v
)=u + v.
50 Глава 2. Линейная алгебра
Полученное равенство означает, что имеется вектор u
+ v
в пространстве
V , который под действием оператора ϕ переходит в вектор u + v. Следова-
тельно, u + v ∈ Im ϕ, и устойчивость образа относительно суммы доказана.
Остается доказать устойчивость относительно скалярного кратного. Пусть
u ∈ Im ϕ. Тогда существует вектор v
∈ V такой, что ϕu
= u. Подействуем
оператором ϕ на скалярное кратное αu вектора u
:
ϕ(αu
)=αϕ(u
)=αu .
Таким образом, существует вектор αu
в пространстве V , который под дей-
ствием оператора ϕ переходит в вектор αu. Следовательно, αu ∈ Im ϕ,и
устойчивость образа относительно скалярного кратного доказана. Это зна-
чит, что образ линейного оператора ϕ является векторным подпростран-
ством в пространстве V .
Теорема доказана.
Определение 25 (вырожденность и невырожденность) Линейный
оператор ϕ, действующий в векторном пространстве V , называется невы-
рожденным, если его ядро является нулевым:
Ker ϕ =0.
В противном случае оператор ϕ называется вырожденным.
Пример 36 Рассмотренные выше проекторы (см. пример 29, стр. 45) в силу дан-
ного только что определения являются вырожденными.
С другой стороны, такие преобразования, как повороты R
α
(см. пример 30, стр. 46),
симметрии Q
x
и Q
y
(см. пример 31, стр. 46), масштабирования S
k
1
,k
2
(см. при-
мер 32, стр. 47) невырожденны.
2.3.3 Алгебра линейных операторов
С линейными операторами можно выполнять все те действия, которые вы-
полняются с элементами алгебр: сложение, умножение и скалярное кратное.
В некоторых случаях можно выполнять еще обращение линейного опера-
тора.
В этом разделе мы дадим определения и докажем, что множество операто-
ров, действующих в данном векторном пространстве является алгеброй.
Определение 26 (сумма линейных операторов) Пусть V — векторное
пространство, и пусть ϕ, ψ — два линейных оператора, действующие в V .
Их суммой называется отображение
η : V −→ V,
действующее в пространстве V по следующему правилу. Каждому вектору
v из V оно ставит в соответствие сумму векторов ϕ(v) и ψ(v):
η(v)=ϕ(v)+ψ(v) .
