Мосин В.Г. Математические основы компьютерной графики: Монография
Подождите немного. Документ загружается.


2.1. Полная матричная алгебра 21
Пример 6 Например, выполняя следующее умножение, получим матрицу 2 ×3:
22
12
1 −12
311
=
806
714
.
Однако для этой же пары множителей не существует произведения в обратном
порядке:
1 −12
311
22
12
.
Причина этого очень проста: число столбцов в первом множителе не совпадает
с числом строк во втором множителе. Попробуйте перемножить эти матрицы,
пользуясь определением — ничего не получится.
Если речь идет о произведении двух квадратных матриц одного порядка, то
такое произведение всегда возможно. Однако и в этом случае существенную
роль играет порядок следования множителей в произведении. Мы вернемся
к этому в следующем разделе (см. теор. 2, стр. 22) при исследовании свойств
полной матричной алгебры. Пока же остановимся на свойствах нулевой и
единичной матриц.
Пример 7 Умножение любой матрицы на единичную не изменяет ее, причем не
важно, с какой стороны проводить это умножение, слева или справа:
10
01
21
−43
=
21
−43
,
21
−43
10
01
=
21
−43
.
Умножение любой матрицы на нулевую дает в результате нулевую матрицу, при-
чем не важно, с какой стороны производится умножение.
00
00
21
−43
=
00
00
,
21
−43
00
00
=
00
00
.
Разумеется, эти свойства остаются справедливыми для квадратных матриц лю-
бого порядка.
2.1.2 Полная матричная алгебра
В этом разделе мы покажем, что множество всех квадратных матриц одного
порядка образует алгебру (см. теор. 1, стр. 22), и опишем некоторые ее
свойства.
Определение 6 (алгебра) Множество M элементов произвольной при-
роды, снабженное двумя внутренними операциями — сложением и умноже-
нием, и одной внешней — умножением на число
4
, называется алгеброй.
Другими словами, множество M называется алгеброй, если:
1. для любых элементов a и b из множества M найдется единственный
элемент c из множества M такой, что: c = a + b,
2. для любых элементов a и b из множества M найдется единственный
элемент c из множества M такой, что: c = ab,
4
Мы называем операции сложения и умножения внутренними, потому что в них участ-
вуют только элементы множества M. Операцию же скалярного кратного мы называем
внешней, потому что в ней участвует число, то есть элемент, не относящийся, вообще
говоря, к множеству M

22 Глава 2. Линейная алгебра
3. для любого элемента a из множества M и числа α найдется единствен-
ный элемент b из множества M такой, что b = αa.
Определение 7 (коммутативная алгебра) Алгебра M называется ком-
мутативной, если множители в призведении можно переставлять местами:
ab = ba ∀ a, b ∈ M.
Определение 8 (ассоциативная алгебра) Алгебра M называется ассо-
циативной, если для любой тройки множителей справедливо следующее
соотношение:
(ab)c = a(bc) ∀ a, b, c ∈ M.
Пример 8 Множество R всех вещественных чисел образует алгебру, так как для
любых двух чисел результатом их умножения
5
и сложения служит число. Эта
алгебра является коммутативной и ассоциативной.
Пример 9 Множество R[x] всех многочленов от переменной x с вещественными
коэффициентами образует алгебру, так как оно устойчиво относительно сложе-
ния, умножения и умножения на число. Действительно, пусть f,g ∈ R[x].Тогда
f + g ∈ R[x], fg ∈ R[x], αf ∈ R[x]. Эта алгебра также является коммутативной и
ассоциативной.
Теорема 1 (о полной матричной алгебре) Множество всех квадратных
матриц порядка n образует алгебру. Она обозначается Matr
n
и называется
полной матричной алгеброй.
Доказательство Покажем замкнутость множества квадратных матриц
относительно характеристических операций алгебры:
1. Пусть A, B, ∈ Matr
n
. Тогда, согласно определению (см. опр. 3, стр. 19),
их сумма — это тоже кадратная матрица того же порядка, что и сла-
гаемые, то есть A + B ∈ Matr
n
.
2. Пусть A, B, ∈ Matr
n
. Тогда, согласно определению (см. опр. 5, стр. 20),
их произведение — это тоже кадратная матрица того же порядка, что
и множители, то есть AB ∈ Matr
n
.
3. Пусть, наконец, A ∈ Matr
n
, α ∈ R. Тогда, согласно определению (см.
опр. 4, стр. 19), выражение αA — квадратная матрица того же поряка,
что и A, то есть αA ∈ Matr
n
.
Итак, множество Matr
n
замкнуто относительно трех операций: сложения,
умножения и умножения на число. Следовательно, по определению (см.
опр. 6, стр. 21), оно является алгеброй.
Теорема доказана.
Теорема 2 (о некоммутативности матричной алгебры) Полная мат-
ричная алгебра является некоммутативной.
5
В этом частном случае число выступает в качестве внутреннего элемента алгебры.
Однако так бывает далеко не всегда.
2.1. Полная матричная алгебра 23
Доказательство Согласно определению (см. опр. 7, стр. 22), для дока-
зательства некоммутативности полной матричной алгебры нам достаточно
привести один пример, демонстрирующий, что на множестве матриц нель-
зя переставлять местами множители. Ограничимся случаем матриц второго
порядка. Возьмем две квадратные матрицы и перемножим их:
11
−21
−1 −1
01
=
−10
23
,
после чего — выполним умножение тех же матриц в обратном проядке:
−1 −1
01
11
−21
=
1 −2
−21
.
Мы видим, что результат умножения зависит от порядка следования мно-
жителей, то есть – матричное умножение некоммутативно.
Теорема доказана.
Теорема 3 (об ассоциативности матричной алгебры) Полная матрич-
ная алгебра является ассоциативной.
Доказательство Согласно определению ассоциативности умножения (см.
опр. 8, стр. 22), нам достаточно показать, что для любых трех матриц A,
B, C из Matr
n
справедливо:
A(BC)=(AB)C.
Доказательство проведем прямым вычислением. Обозначим
F = A(BC) ,G=(AB)C
и покажем, что матричные компоненты f
ij
равны соответствующим компо-
нентам g
ij
.ПустьS = BC. Тогда, согласно определению (см. опр. 5, стр. 20),
s
ij
=
n
k=1
b
ik
c
kj
.
Следовательно, для вычисления компонент f
ij
нам потребуется взять двой-
ную сумму (еще раз см. опр. 5, стр. 20):
f
ij
=
n
l=1
a
il
s
lj
=
n
l=1
a
il
n
k=1
b
lk
c
kj
=
n
l=1
n
k=1
a
il
b
lk
c
kj
.
Пусть далее Q = AB. Тогда, согласно определению (см. опр. 5, стр. 20),
q
ij
=
n
l=1
a
il
b
lj
.
Следовательно, для вычисления компонент g
ij
нам опять потребуется взять
двойную сумму (и еще раз см. опр. 5, стр. 20):
g
ij
=
n
k=1
q
ik
c
kj
=
n
k=1
n
l=1
a
il
b
lk
c
kj
.

24 Глава 2. Линейная алгебра
Сравнивая полученные выражения для компонент f
ij
и g
ij
, приходим к
выводу об их идентичности (второе отличается от первого только порядком
слагаемых, который, как известно, не влияет на сумму). Следовательно,
F = G.
Теорема доказана
6
.
Итак, матричное умножение, с одной сотроны, напоминает это действие в
его обычном понимании — умножение чисел или функций обладает свой-
ством ассоциативности, а с другой стороны — отличается тем, что является
некомутативной операцией.
Кроме того, следует иметь в виду, что в полной матричной алгебре при
умножении двух ненулевых элементов результат может оказаться нулем
(другими словами полная матричная алгебра содержит так называемые де-
лители нуля), что также отличает ее от числовых (см. пример 8, стр. 22)
или функциональных (см. пример 9, стр. 22) алгебр.
Теорема 4 (о делителях нуля) Полная матричная алгебра содержит де-
лители нуля.
Доказательство Для доказательства нам достаточно привести один со-
ответствующий пример. Ограничимся случаем матриц второго порядка:
10
00
00
01
=
00
00
.
Теорема доказана.
2.1.3 Матричное обращение
Еще одним арифметическим действием, помимо сложения, умножения и
скалярного кратного, является деление чисел или функций. Операцию де-
ления на множестве матриц невозможно определить в силу некоммутатив-
ности матричного умножения
7
. Однако во многих случаях (см. критерий
обратимости, теор. 8, стр. 27) можно выполнять так называемое матрич-
ное обращение (аналог алгебраического обращения на множестве чисел или
функций).
Определение 9 (обратная матрица) Пусть A — некоторая матрица из
полной матричной алгебры Matr
n
. Если существует матрица X ∈ Matr
n
такая, что
AX = E, XA= E,
то матрица X называется обратной к матрице A и обозначается A
−1
. Мат-
рица, обладающая обратной, называется обратимой.
Теорема 5 (единственность обратной матрицы) Если обратная мат-
рица существует, то она единственна.
6
Доказанная теорема позволяет говорить о матричных степенях. Действительно, так
как в выражении A · A · A ···A все равно каким образом расставлять скобки, его можно
обозначить просто как A
n
.
7
Действительно, пусть α/β — рациональная (числовая или функциональная) дробь.
Тогда очевидно, что α/β = α · (1/β), и, вместе с тем, α/β =(1/β) · α. Некоммутативность
же умножения означает, что правые части этих выражений различны.

2.1. Полная матричная алгебра 25
Доказательство Пусть матрица A ∈ Matr
n
обратима. Допустим, что су-
ществуют две различные матрицы X, Y ∈ Matr
n
такие, что
X = A
−1
,Y= A
−1
.
Первое из этих соотношений означает по определению (см. опр. 9, стр. 24),
что
XA = E.
Умножим это равенство на Y справа:
XAY = EY .
В силу ассоциативности матричного умножения (см. теор. 3, стр. 23) мы
можем расставить скобки в правой части так, как нам это удобно. Сделаем
это следующим образом:
X(AY )=EY .
Так как, согласно предположению, Y = A
−1
, выражение AY , по определе-
нию (см. опр. 9, стр. 24), дает единичную матрицу. Следовательно,
XE = EY ,
откуда X = Y . Но это противоречит нашему предположению о том, что
матрицы X и Y различны.
Теорема доказана.
Теорема 6 (об обращении произведения) Пусть матрицы A и B обра-
тимы. Тогда обратима и матрица AB, причем,
(AB)
−1
= B
−1
A
−1
.
Доказательство Нам достаточно показать, что произведение матриц AB
и B
−1
A
−1
дает единичную матрицу. Действительно:
(AB)(B
−1
A
−1
)=A(BB
−1
)A
−1
= AEA
−1
= AA
−1
= E.
В этой несложной выкладке мы, как и при доказательстве предыдущей тео-
ремы, использовали ассоциативность матричного умножения (см. теор. 3,
стр. 23) и определение обратной матрицы (см. опр. 9, стр. 24).
Теорема доказана
8
.
Следующая теорема дает метод
9
вычисления обратных матриц. Прежде,
чем приступать к изучению этого теоретического блока, необходимо ознако-
миться с содержанием приложения, посвященного определителям (см. при-
ложение A.1, стр. 157), так как техника вычисления определителей является
основой данного метода матричного обращения.
8
Вообще, если речь идет об обращении произведения любого числа обратимых матриц,
то из доказанной теоремы вытекает следующая формула:
(A
1
A
2
...A
n
)
−1
= A
−1
n
A
−1
n−1
...A
−1
1
,
то есть — обращение произведения равно произведению обращений, взятых в обратном
порядке.
9
Отметим, что это не единственный и далеко не всегда наиболее эффективный метод
матричного обращения. В приложениях (см. приложение A, стр. 157) мы, помимо это-
го, рассматриваем еще так называемый метод Гаусса вычисления обратных матриц. В
дальнейшем при изложении теоретического курса мы используем оба метода.
26 Глава 2. Линейная алгебра
Теорема 7 (о вычислении обратной матрицы) Пусть матрица A об-
ратима. Тогда матрица A
−1
может быть вычислена по следующей формуле:
A
−1
=
1
|A|
(
˜
A)
T
,
где
˜
A — матрица, составленная из алгебраических дополнений к элементам
матрицы A,аT означает транспонирование.
Доказательство Обозначим
B = A ·
1
|A|
(
˜
A)
T
.
Нам нужно показать, что B — это на самом деле единичная матрица. Тогда,
согласно определению (см. опр. 9, стр. 24) это будет означать, что матрица
1
|A|
(
˜
A)
T
является обратной к матрице A.
B =
a
11
a
12
... a
1n
a
21
a
22
... a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
... a
nn
1
|A|
A
11
A
12
... A
1n
A
21
A
22
... A
2n
.
.
.
.
.
.
.
.
.
.
.
.
A
n1
A
n2
... A
nn
T
=
=
1
|A|
a
11
a
12
... a
1n
a
21
a
22
... a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
n2
... a
nn
A
11
A
21
... A
n1
A
12
A
22
... A
n2
.
.
.
.
.
.
.
.
.
.
.
.
A
1n
A
2n
... A
nn
.
Выполняя матричное умножение, получим следующее выражение для ком-
понент b
ij
:
b
ij
=
1
|A|
(a
i1
A
j1
+ a
i2
A
j2
+ ···+ a
in
A
jn
)=
1
|A|
|A| если i = j,
0 если i = j.
Последнее звено в этом равенстве получается в силу теорем о разложении
определителя по строке и о разложении определителя по чужой строке.
Таким образом,
b
ij
=
1
|A|
|A| если i = j,
0 если i = j ;
=
1 если i = j,
0 если i = j.
Следовательно, B = E.
Теорема доказана.
Пример 10 Вычислим матрицу, обратную к A =
12
1 −1
. Нам нужно знать:
определитель матрицы и четыре алгебраических дополнения к каждому матрич-
ному месту.
|A| =
12
1 −1
= −1 −2=−3.

2.2. Векторные пространства 27
Далее вычислим алгебраические дополнения:
A
11
= −1; A
12
=(−1)1 = − 1;
A
21
=(−1)2 = −2; A
22
=1.
Составим матрицу
˜
A и транспонированную к ней:
˜
A =
−1 −1
−21
, (
˜
A)
T
=
−1 −2
−11
.
Следовательно, A
−1
= −
1
3
−1 −2
−11
=
1/32/3
1/3 −1/3
.
Выполним проверку:
1/32/3
1/3 −1/3
12
1 −1
=
10
01
.
В результате умножения мы получили единичную матрицу. Задача решена верно.
В заключение этого раздела приведем условие, необходимое и достаточное
для того, чтобы матрица была обратима.
Теорема 8 (критерий обратимости) Матрица обратима тогда и только
тогда, когда она невырождена
10
.
Доказательство Доказательство напрямую вытекает из доказанных вы-
ше теорем: о единственности обратной матрицы (см. теор. 5, стр. 24) и о ее
вычислении (см. теор. 7, стр. 26).
Теорема доказана.
Продолжая аналогию с числовыми действиями, отметим следующее: на
множестве чисел существует единственный необратимый элемент — ноль.
На множестве матриц необратимых элементов бесконечно много: любая вы-
рожденная матрица необратима.
2.2 Векторные пространства
Численное описание проебразований плоскости, которое является нашей ко-
нечной целью, требует детального изучения самого объекта преобразования
— плоскости. С точки зрания линейной алгебры плоскость является двумер-
ным векторным пространством, и мы рассмотрим основы теории векторных
пространств, чтобы в дальнейшем приложить их к конкретной (двумерной)
ситуации.
Практические примеры, относящиеся к этому разделу, представлены в при-
ложениях (см. приложение B.1, стр. 188).
10
Напомним, что невырожденной называется матрица, определитель кторой отличен
от нуля.
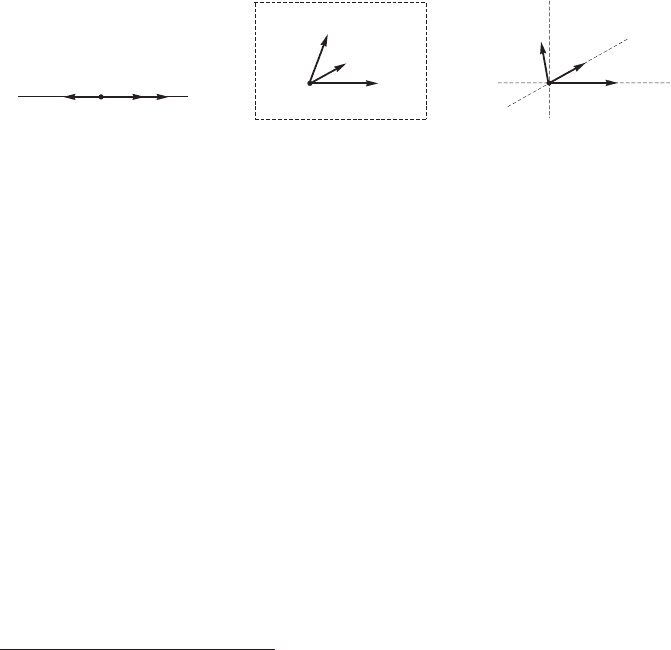
28 Глава 2. Линейная алгебра
2.2.1 Определения и примеры
Определение 10 (векторное пространство) Множество V называется
векторным пространством, если оно замкнуто относительно двух операций:
сложения и умножения на число. То есть:
1. для любых двух векторов v
1
и v
2
из векторного пространства V най-
дется единственный вектор v
1
+ v
2
, принадлежащий V ;
2. для любого вектора v из векторного пространства V и для любого
вещественного числа α найдется единственный вектор αv, принадле-
жащий V .
Заметим, что данное выше определение алгебры (см. опр. 6, стр. 21) слу-
жит обобщением для понятия векторного пространства. Алгебры обладают,
помимо сложения и умножения на число, еще одной операцией — умноже-
нием. Таким образом, любая алгебра является векторным пространством,
обратное неверно.
Пример 11 (прямая, плоскость, физическое пространство) Рассмотрим се-
рию геометрических примеров (см. рис. 2.1, стр. 28).
0
u
v
w
l
(a) Прямая.
0
u
v
w
π
(b) Плоскость.
0
u
v
w
R
3
(c) Физическое простран-
ство.
Рис. 2.1: Геометрическая серия примеров векторных пространств.
1. Зафиксируем на прямой l точку O и будем прикладывать в точке O все-
возможные векторы таким образом, чтобы их концы оставались на l.Ор-
ганизованное таким образом множество векторов является векторным про-
странством.
2. Зафиксируем на плоскости π точку O и будем прикладывать в точке O
всевозможные векторы таким образом, чтобы их концы оставались на π.
Организованное таким образом множество векторов является векторным
пространством.
3. Зафиксируем в физическом
11
пространстве R
3
точку O и будем прикла-
дывать в точке O всевозможные векторы таким образом, чтобы их концы
оставались в R
3
. Организованное таким образом множество векторов явля-
ется векторным пространством.
Отметим сразу же, что окружность, парабола, эллипсоид, цилиндр, пара-
болоид и, вообще, все криволинейные геоматрические объекты не являются
векторными пространствами. Вся геометрическая серия примеров вектор-
ных пространств исчерпыватся приведенными выше.
11
Допуская некоторую вольность, мы будем называть физическим пространством все
пространство физического (то есть — реального) мира.

2.2. Векторные пространства 29
Пример 12 (простанства строк) Это серия примеров является классической
алгебраической интерпретацией понятия векторного пространства. Как мы уви-
дим в дальнейшем, если в векторном пространстве фиксирован базис, то оно одно-
значно реализуется в виде пространства строк (или столбцов, дело вкуса) чисел,
являющихся координатами его векторов.
Рассмотрим множество R
n
= {(x
1
,x
2
,...x
n
)} всевозможных упорядоченных на-
боров чисел и определим на этом множестве операции сложения и умножения на
число следующим образом:
(x
1
,x
2
,...x
n
)+(y
1
,y
2
,...y
n
)=(x
1
+ y
1
,x
2
+ y
2
,...x
n
+ y
n
) ,
α(x
1
,x
2
,...x
n
)=(αx
1
,αx
2
,...αx
n
) .
По определению, множество R
n
с описанными операциями сложения и скалярного
кратного является векторным пространством.
Отметим здесь же несколько частных случаев.
1. Пространство строк длины 1. Это просто множество чисел. Таким образом,
множество чисел R является векторным пространством.
2. Пространство строк длины 2. Это — множество пар чисел. Таким образом,
множество пар чисел R
2
является векторным пространством.
3. Пространство строк длины 3. Это — множество троек чисел. Таким образом,
множество троек чисел R
3
является векторным пространством
12
.
Вернемся к геометрической серии примеров (см. пример 11, стр. 28). В пер-
вом пункте мы рассматривали прямую, снабженную отмеченной точкой
(своего рода, началом координат). Если при этом указать еще и единицу
масштаба, то тогда каждый вектор прямой описывается одним числом. С
этой точки зрения прямая ничем не отличается от множества строк длины
1 (см. пример 12, стр. 29).
Далее, во втором пункте, мы рассматривали плоскость, снабженную отме-
ченной точкой . Если при этом через отмеченную точку провести две оси
(не обязательно перпендикулярные) и указать две единицы масштаба (они
могут быть различными для обеих осей), то тогда каждый вектор плоско-
сти описывается парой чисел — координатами своего конца. С этой точки
зрения плоскость ничем не отличается от множества строк длины 2 ( см.
пример 12, стр. 29).
Наконец, в третьем пункте мы рассматривали физическое пространство,
снабженное отмеченной точкой . Если при этом через отмеченную точку
провести три оси и указать три единицы масштаба, то тогда каждый век-
тор физического пространства описывается тройкой чисел — координатами
своего конца. С этой точки зрения физическое пространство ничем не от-
личается от множества строк длины 3 (см. пример 12, стр. 29)
13
.
Многие математические множества (например, алгебры или векторные про-
странства), обладающие идентичной структурой, в ряде случаев удобно бы-
вает не отличать друг от друга. Такие объекты называются изоморфными.
Так, например, мы убедились, что прямая изоморфна множеству чисел,
12
Заметьте, что выше мы уже обозначали символом R
3
физическое пространство.
13
Теперь понятно, почему мы используем для этих пространств одно и то же обозна-
чение?
30 Глава 2. Линейная алгебра
плоскость — множеству пар чисел, физическое пространство — множеству
троек числ.
С точки зрения теории векторных пространств изоморфные пространства
неотличимы друг от друга, и можно считать, что это одно и то же.
Пример 13 (множество многочленов) Множество R[x] многочленов от пе-
ременной x с вещественными коэффициентами образует алгебру (см. пример 9,
стр. 22). Следовательно, это множество является векторным пространством (см.
опр. 10, стр. 28).
Пример 14 Множество R
n
[x] многочленов от переменной x фиксированной сте-
пени n с вещественными коэффициентами не является векторным пространством.
Действительно, мы легко можем показать, что R
n
[x] не устойчиво относительно
суммы. Пусть, например,
f(x)=x
n
+1,g(x)=−x
n
+ x − 2 . Тогда f(x)+g(x)=x − 1 .
Таким образом, f(x)+g(x) имеет степень, отличную от n, и, следовательно, мно-
жество R
n
[x] не является векторным пространством, так как оно не обладает
устойчивостью относительно суммы.
Пример 15 Множество R
≤n
[x] многочленов от переменной x, степень которых
не превосходит n, является векторным пространством. Действительно, при сло-
жении двух многочленов f (x) и g(x) из R
≤n
[x] степень суммы не превзойдет наи-
большей из степеней слагаемых, то есть — не превзойдет n, что означает устойчи-
вость множества отностиельно суммы. При умножении же многочлена на число
его степень не изменяется, что демонстрирует устойчивость множества R
≤n
[x]
отностиельно скалярного кратного.
Задержимся на этом примере и рассмотрим один частный случай. Пусть n =1.
Тогда
R
≤1
[x]={α + βx |α, β ∈ R}.
Мы видим, что множество многочленов, степень которых не превосходит еди-
ницы, характеризуется парами чисел: свободным членом α и коэффициентом β.
Сравнивая этот факт с результатами, полученными нами выше (см. пример 11,
стр. 28 и пример 12, стр. 29), приходим к заключению, что множество R
≤1
[x]
изоморфно плоскости.
2.2.2 Линейная зависимость и линейная независимость
систем векторов
Этот раздел является подготовительным к следующему, где мы введем по-
нятие базиса векторного простанства (как некоего инструмента его числен-
ного измерения).
Ключевым для понимания дальнейшего изложения служит понятие линей-
ного комбинирования, при выполнении которого необходимы навыки в ре-
шении линейных алгебраических систем. Сооттветствующие примеры и ме-
тоды приведены в приложениях (см. приложение A.3, стр. 174).
Определение 11 (линейная комбинация векторов) Пусть V — вектор-
ное пространство, v
1
,v
2
,...,v
n
∈ V — векторы этого пространства. Их ли-
нейной комбинацией называется выражение
α
1
v
1
+ α
2
v
2
+ ···+ α
n
v
n
,
где α
1
,α
2
,...,α
n
— некоторые числовые коэффициенты.
