Мошинский Л. Эпоксидные смолы и отвердители
Подождите немного. Документ загружается.


·341·
Схема
32:
У
=
50.1
+
6.8ч
-
4.9ч
+12.6x1X2
-7.8ч2
-
2'3Х22
Результаты
такого
абстрактного
эксперимента
показаны
в
первой
строке
ТаБЛИЦЫ
9.9.
Традиционная
схема
обработки
результатов
абстрактного
эксперимента
дает
исходное
уравнение
(32),
но
с
небольшой
систематической
погрешностью
8
свобод-
нам
члене:
Схема
33:
УТС
= 49.3 +
6.8ХI
-4.9Х2
+12.6XJЧ
-7.8xI2 -
2.3ч
2
Эта
погрешность
переходит
в
рассчитанные
значения
резу"ь
татов.
В
противопо
ЛОЖНОСТЬ
этому.
обработка
резул!:>
татов
абстрактного
эксперимента
с
использова
нием
предложенного
алгоритма
дает
ПКУ,
8
ТОЧНОСТИ
повторяющее
теоретически
заданную
модель
(32):
Схема
34:
Упа
= 50.1 +
6.8ч
-
4.9ч
+12.6XJЧ
-7.8ч2
-
2.3ч
2
Расхождение
в
свобоДНОМ
члене
полного
квадраТНОГО
уравнения
и
его
ли
нейных
эффектах
еще
более
заметно
при
обработке
экспериментальных
данных.
Для
подтверждения
3TOfO,
в
таблице
9.9
прмведены
результаты
исследования
двух
зпаксИДНЫХ
полимеров,
Ниже,
на
схемах
(35)
и
(36)
даны
полные
квадратные
ураВ
нения
регрессии,
полученные
при
обработке
этих
результатов
как
по
традиционной
схеме
(тс),
так
и
с
использованием
предложенного
алгоритма
(па).
Здесь
же для
сравнения
даны
неполные
квадратные
уравнения,
исправленные
методом
УВП:
-
температура
стеклования
эпоксидного
полимера,
ос
(У,)
Схема
35:
Ytтc
= 62.9 +
13.5Х(
+
7.4ч
+
2.5Х(Х2
-17.2Х(2
-
23.1ч
2
Ytna = 66.5 +
12.3ХI
+
6.4Х2
+
2.5Х(Х2
-17.2Х(2
-
23.1ч
2
У
ty.
=
(26.2+12.3ХI
+6.4ч+2.5Х(ч)(2.557-1.020Х(
2-О.537ч2)
-
разрушающее
напряжение
при
сжатии
эпоксидного
полимера,
МПа
(У2)
Схема
36:
У2тс
= 46.5 -
23.0Х(
+
19.4Х2
+
3.7Х(Х2
+
20.0Х(2
-
3.6ч
2
У2па
= 52.2 -
18.0Х(
-
22.1ч
+
3.7ХIЧ
+
2О.0Х(2
-
3.6ч
2
У
2у.
=
(68.6-18.0Х(-22.1
ч+3.7ХIЧ)(О.
73+0.12Х(2+0.
15
ч
2
)
Анализ
Данных
таБЛИЦЫ
9.9
позволяет
сделать
вывод,
что
все три
типа
матема
тических
моделей
феноменологически
состоятельны.
Однако,
они
позволяют
пред
сказать
значения
naраметров
с
разной
точностью:

у
(температрура
стекло-
вания,
С)
у
(разрушающее
напряже-
ние при
сжа
тии,
МПа\
у
(теоретически
заданная
модель)
CTaкдapr
.оспрои_.оД8lКОC'Rf
д&llНlDt:
•
трaдмqиОН-
•
npeДnO-
•
и.тОД.
КОЙ
czeиe
..
икон
)'Вп
"'..0_
1.87
(21\
1.08
(21\
3.15
1.41
(66\
1.59
(66)
2.80
1.45
0.00
(12
)
(38)
(Количество
степеней
свободы
при
рассчете
стантарта
воспроизводимости
дано
е
скобках.)
Приведенные
выше
данные
выгnядели
бы
менее
блaronoлучно,
если
бы
лри
расчете
дисперсий
ИСПОЛЬ30В8лось
меньшее
количество степеней свободы,
т
.е.
в
каждом
олыте
было
бы
сделано
меньшее
количество
испытаний.
Обычно
при
noлу
чении
статистически
неблагополучных
данных
рекомендуется
оценивать
значи
мость
различия
дисперсий,
налример,
с
использованием
известного
статмстичес
I(ОГО
критерия
Фишера.
Оценку
статистических
гипотез
следует
проводить
тогда,
когда
возникает
нeonределенная
сктуация
и
необходимо
принять
решение.
При
этом
имеет
смысл
помнить,
что
ни
одна
принятая
или
отвеprнyтая
статистическая
гипотеЗ8
не
может
доказать
(или
опроверrнyn.)
сформулированного
предnoло
жения.
В
частности,
прмнятая
статистическая
гипотеза
говорит
лишь
о
том, что
данное
предположение
согласуется
со
статистическим
распределением
получен
ных
экспериментальных
данных.
Подобным
образом
можно
относиться
и
к
оцени
ванию
значимости
коэффициентов
регрессии.
Здесь
хотелось
бы
сделать
очень
важное
замечание.
Существуют
статистические
процедуры,
которые
позволяют
оценить
коэффи
циент
регрессии
с
точки
зрения
-
отражает,
или
не
отражает
ero
величина
действие
изучаемых
факторов.
При
таком
оценивании
коэффициент
регрессии
может
ока
заться
значимым,
или
незначимым.
Однако,
категорическое
требование
исключать
из
уравнения
регрессии
незначимые
коэффициенты
представляется
попросту
бес
содержательным.
Нужно
иметь
ВВМДУ,
что
tteзначимые
коэффициенты
регрессии,
практически,
не
влияют
ни на
вид
аппрсжсимирующеМ
функции,
ни на
положение
оптимума,
ни на
направление
градиента
поверхности
отклика.
С
ДРУГОЙ
стороны,
исключение
незначимых
коэффициентов
из
уравнения
регрессии
часто
делает
мо
дель
не очень
красивой,
а
вычисленные
значения
параметров
-
эмоционально
ме·
нее точными.
Экспериментатору
фактически
приходится
выбирать
между
аб
страктной
статистической
строгостью
и
эстетичностью
модели.
Поэтому
в
каждом
конкретном
случае
экспериментатор
должен
решить:
исключать,
или
не
исключать
незначимый
коэффициент
регрессии.
Когда
мы
говорили
об
эстети,",ности
модели,
то
имели
ввиду
эмоциональное
восприятие
результатов
соответствующих
расчетов.
Напомним,
что
значения
изу
чаемого
параметра
можно
рассчитать,
используя
для
этого
уравнение
регрессии,
Рассчетные
величины
в
точках
плана
MOryт
ТО,",НО
совпадать
с
результатами
Эl(спе·
римента
(или
MOryт
быть
им
близки)
и
тогда
мы
говорим,
,",то
уравнение
регрессии
является
адекватной
моделью
экспериментальной
зависимости.
При
этом
нужно
иметь
ввиду,
что
такая
адекватность
распространяется
лишь
на область
фактор
ного
квадрата
(кvбa,
гиперкуба)
и
непосредственно
примыкающие
к
нему
части
фак-

-343-
торного
простанства.
Если налицо
существенные
расхождения
между
экспери·
ментальными
данными
и
результатами
расчетов,
то
мы
ГОВОРИМ,
что
полученная
матаматическая
модель
не
адекватна
изучаемой
зависимости.
Такие
расхождения
обычно
связаны
с
тем,
что
резуль
таты
эксперимента
в
принципе
не
MOIYТ
быть
опи
саны
полиномом
второго
порядка'nричин
ЭТОГО
может
БЫTh
много, В
частности,
эксперименальная
зависимость
сильно
растянута,
или
чрезмерно
ассиммеТрична
и
Т.Д.
В
практике
экспериментальной
работы
очень
редко
встречаются
случаи,
когда
полное
квадратное
уравнение
приходится
рассматривать
как
недостаточно
точную
модель
экспериментальной
зависимости.
В
таких
случаях
для
повышения
ТОЧНОСТИ
и
прогностичности
модели
можно
рекомендовать
метод
матемаТИ'4еского
преобра~
зования
изучаемorо
параметра.
Этот
метод
иногда
позволяет
построить
модель
с
необходимой
точностью
предсказания
при
использовании
уже
ПОЛY'-lенных
экспе~
риментальных
данных.
Ре'4ь
идет о
том,
'4то
изучаемый
параметр
можно
заменить
его
однозна'4НОЙ
функцией.
что
должно
произвести
сжатие
растянутой
зависимости.
или
симметризацию
деформированной
экспериментальной
поверхности.
К
сожале
нию,
автору
не известны
общие
правила
осуществления
этого
метода
-
эмпири
ческие
приемы,
которыми
пользовапся
сам
автор
достаточно
громоздки.
Однако,
затраты
на
вычиспительные
эксперименты
подобного
рода
всегда
меньше,
чем
на
новую
серию
опытов,
даже
если
такие
опыты
снова
проводятся
с
привneчением
статистических
методов
планирования
экспериментов.
Техника
преобразования
параметра
и
обработки
результатов
экспериментов
дос
таточно
проста.
Прежде
всего
выбирают
однозначную
функцию
параметра
У
Z=F(Y
,
).
Для
каждого
экспериментального
значения
параметра
вычисляют
значение
функции
Z.
и
затем
обычным
способом
рассчитывают
уравнение
регрессии.
но
для
преобразованного
параметра
z..
Подходящими
для
этой
цели
выражениями
можно
считать
функции
вида:
Схема
37:
Более
сложными,
но
вполне
лриемлемыми
преобразованиями
для
эксперимен
тального
параметра
являются
функции
Z(y,
х"
Х
2
).
налример:
Схема
38:
где
д,
В,
С·
эмпирические
коэффициенты,
которые
подбираются
с
ломощью
ком
пьютера,
или
вручную
методом
Мпроб
и
ошибок
М
,
е
-
основание
натуральных
лorа
рифмов.
После
обработхи
данных
плана
с
преобразованным
параметром
получают
новое
уравнение
регрессии:
Схема
39:

Реконструщия
зависимости
исходного
naраметра
не
представляет
труда.
Еспи
ПКУ
(39)
обозначить
Z = f(X,.
Х
2
),
то
реконструируемая
зависимость будет
выгпядеть
спедущим
образом:
Схема
40:
Ниже
в
таблице
10.9,
приведены
данные,
иллюстрирующие
методику
преобразова
ния цепевого
параметра
при
планировании
экспериментов.
8
процессе
изучения
разрушающего
напряжения
при
изгибе
эпоксидного
полимера
(=FS, Flexural
Stгепgth.
МПа)
был
выполнен
ЦКОП
второго
порядка
и
рассчитано
уравнение
ре
грессии:
Схема
41:
FS
=91.9-28.4x
1
+
16.4Х2+З.5ХIХ2+4.2х~
+
2.0x~
Но
Om.no08
Опыт
1
Опыт
2
Опыт
3
Опыт
4
Опыт
5
Опыт
6
Опыт
7
Опыт
8
Опыт
9
Таблица
10.9
ДаННI.Ie.
иллюстрирующие
методику
обработки
результатов
эксперимента
с
преобразованием
целевого параметра.
+
о
о
о
+
+
о
о
+
о
FS,
МI"1a
Найд.
8.rч.
F(Y,
Х
1
•
Х
2
)
1
2 3
88.6 88.6
140.4 140.4
48.8 48.8
114.6 114.6
76.466.7
133.6 125.5
121.1110.3
84.4
77.5
83.0
91.9
1.309
2.150
1.309
2.150
1.579
2.420
1.730
1.730
1.500
z ....
4
67.7
65.3
37.3
53.3
48.4
55.2
70.0
48.8
55.3
5
67.7
65.3
37.3
53.3
48.5
55.3
69.9
48.7
55.3
FS.uo.: •
Мna
6
88.6
140.4
48.8
114.6
76.6
133.8
120.9
84.2
83.
О
Приме
..
анме:
первый
стопбец
(найд.)
экспериментальные
значения
разрушающего
напряжения
при
изгибе:
второй
столбец
(аыч.)
-
значения
параметра.
вычисленного
с
использоаанием
уравнения
регрессии
(41):
последний
столбец
(FS
выч
)
•
значения
разрушаю
щего
напряжения
при
изгибе.
аычисленного
с
учетом
откорректированного
уравнения
регрессии.
Значения
остальных
величин
разъяснены
ниже
е
тексте.
с
точки
зрения
поставпенной
задачи,
полное
квадратное
уравнение
не
позво
лило
с
достаточной
точностью
аппроксимировать
экспериментальные
данные
(таб
лица
10.9,
ср.
столбцы
1
и
2).
Поэтому
для
обработки
результатов
экспериментов
был
применен
метод
преобра3Qвания
параметра,
В
качестве
преобразующ8Й
фун
кции
было
использовано
выражение:

·345·
Схема
42:
rAe
F(xpxz)
=
А
-
B[sin(Xl)
+
СОЭ(Хг)
J
где
Х1
•
соотношение
ароматических
аминов
в
отеерДителе.
Х2'
количество
МОДИфикатора.
циклоаЛИфатической
ЭПОКСИДНОЙ
СМОЛЫ,
%
от
массы
отвердителя
Коэффициенты
этого
выражения
были
подобраны
с
ПОМОЩЬЮ
компютера
•
Схема
43:
Zi
=
У'!
2.0
-
O,5[sin(xl)
+
cos(x
z
))
Полное
квадратное
уравнение,
описывающее
зависимость
преобразованнorо
пара
метра
Z
от
факторов
Х
1
и
Х
2
.
имело
следующий
вид:
Схема
44:
Z = 55.3 -
3.4х
( +
10.6ч
+
4.6Х(
Ч
-
3.4Х(
1 + 4.0
ч
1
выиспенияя
показали (таблица
10.9.
столбцы
4
и
5),
ЧТО
это
уравнение
регрессии
точно
описывает
преобразованную
функцию
Z
80
всех
точках плана.
Реконструк
ЦИЯ
исходного
параметра
была
выполнена
с
использованием
выражения:
Схема
45:
у
= (55.3 -
3.4х(
+
10.6ч
+
4.6х(ч
-
3.4х(1
+
4.0ч
1
).
*
{2
- 0.5[sin(xI> +
соs[ч]}
Уравнение
регрессии
(45)
ТОЧНО
описывало
экспериментальную
зависимость
и в
точках
плана
(таблица
10.9,
столбец
6),
и
в
лримыкающ8Й
области
факторного
пространства,
достаточной
для
оптимизации
техническOfО
решения.
В
закпючение
хотелось
бы
предостеречь
читателей
от
ошибок,
которые
сам
автор
делал
неоднократно.
Нет
смысла
исполь3о8ать
эту
методику,
если
и
без нее
можно
оптимизировать
искомое
техническое
решение.
Эта
методика
весьма
трудо
емка,
требует
большого
терпения
и
особоМ
аккуратности
в
представлении
и
обра
ботке
данных.
80
вторых,
метод
преобраэования
параметров
можно
применять
в
тех
случаях,
когда
эксперимент
выполнен
тщательно
и не
содержит
грубых
ошибок.
Точное
описание
неряшливых
экспериментальных
данных бессмысленно
с
любой
ТОЧКИ
зрения.
Построенне
факторных
днаграмм
н
метод
оптимума
по
Парето.
Выше
уже
упоминалось,
что
целью
мнorих
:жспериментальных
работ является
оптимизация
технического
решения.
С
одной
стороны,
оптимальное
сочетание
по
казателей
изучаемого
объекта,
как
правмло,
реализуется
8
сравнительно
неболь
шой
области
многомерного
пространства.
Ситуация
осnoжняется
тем,
что
опти
мальность
-
это
понятие
эвентуальное,
смысл
которого
зависит
от
цели
проводи
мого
исследования.
С
другой,
оптимизация
любого
объекта
-
это
цепь
при.нятия
решений
и
для
этого
необходимо
наглядное
представление
эксперименталЬНblХ
данных,
без
чего
трудно
понять
структуру
изучаемых
зависимостей.
Напомним,
что
в
научных
работах,
которые
проводятся
традиционными
методами
однофакторного
·3460
:жсneримента,
фУНКЦИЮ
наглядного
представления
данных
ВЫПОЛНЯЮТ
графики,
выражающие
заВИСИМОСТЬ
изучаемого
параметра
от
одного
143
фаКТОРОВ
при
фикси
рованных
значениях
остальных
факторов.
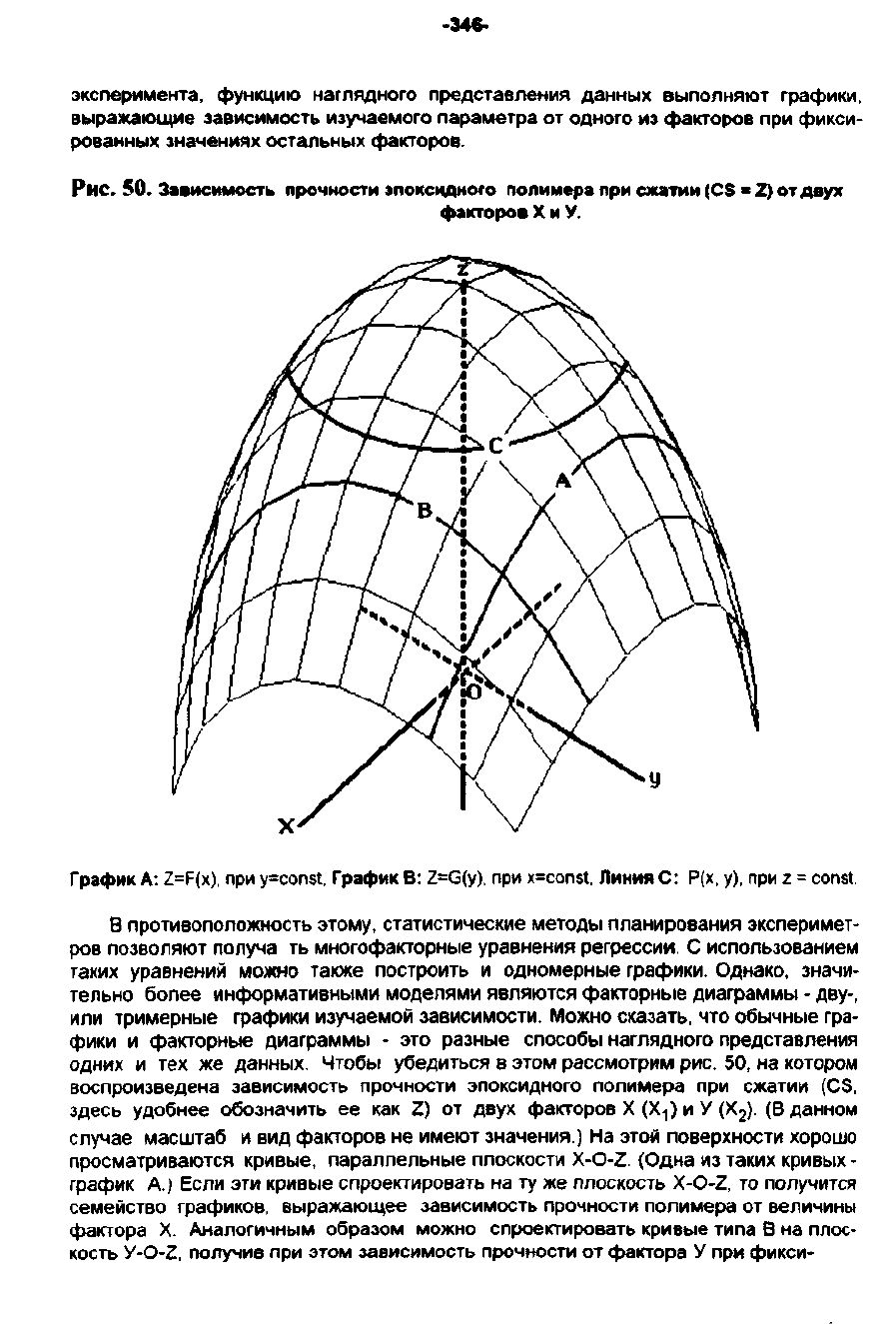
Рис.
50.
38I1МСММОСТIlo
прочноС'Ти
зпоксмднOtО
nonи
..
ер.
при C*lТМИ
IСЗ
• Z)
от
двух
факroРО8
Х
И
У.
ГрафИК
А:
Z=F(x),
при
y=const,
График
В:
Z=G(y).
при
x=const.
ЛИНИЯ
С:
Р(х,
у),
при
z = const.
в
противоположность
этому,
статистические
методы
планирования
зксперимет
~
ров
позволяют
получа
ть
многофакторные
уравнения
регрессии.
С
использованием
таких
уравнений
можно
также
построить
и
одномерные
графики.
Однако,
значи
тельно
более
информативными
моделями
являются
факторные
диаграммы
-
дву-,
или
три
мерные
графики
изучаемой
зависимости.
Можно
сказать,
что
обычные
гра
фИКИ
и
факторные
диаграммы
-
это
разные
способы
наглядного
представления
одних
и тех
же
данных.
Чтобы
убедиться
в
этом
рассмотрим
рис.
50,
на
котором
воспроизведена
зависимость
прочности
эпоксидного
полимера
при
сжатии
(CS,
здесь
удобнее
обозначить ее
как
Z)
от
двух
факrоров
Х
(Х
1
)
и
у
(х
2
).
(6
данном
спучае
масштаб
и
вид
факторов
не
имеют
значения.)
На
этой
ловерхности
хорошо
просматриваются
кривые,
параллельные
плоскости
X-O-z.
(Одна
из
таких
кривых
-
график
А.)
Если
эти
кривые
спроектировать
на
ту
же
плоскость
X-O-Z,
то
получится
семейство
графиков,
выражающее
зависимость
прочности
полимера
от
величины
фактора
Х.
Аналогичным
образом
можно
спроектировать
кривые
типа
В
на
плос
кость
y-O-Z,
получив при
этом
зависимость
прочности
от
фактора
У
при
фикси-
·347·
рованных
значениях
фактора
Х.
Наконец,
на
указанной
поверхности
проведена
ли·
ния
С,
соединяющая
точки,
в
которых
прочность
полимера
при
сжатии
постоянна
и
равна
100
МПа.
Подобные
геодезические
линии
ПРИНЯТО
называть
ЛИНИЯМИ
поста·
янного
уровня,
ИЛИ
крапа
-
изолиниями.
Если
изолинию
С
спроектировать
вниз на
плоскость
Х-О-У, то
получим
двумерный
график,
который
показывает,
при
каких
значениях
факторов
Х
и
У
ПРОЧНОСТЬ
при
сжатии
ЭПОКСИДнога
полимера
равна
100
МПа.
Несколько
таких
проекций
изолиний
е
ограниченной
области
факторной
плоскости
составляют
факторную
диаграмму.
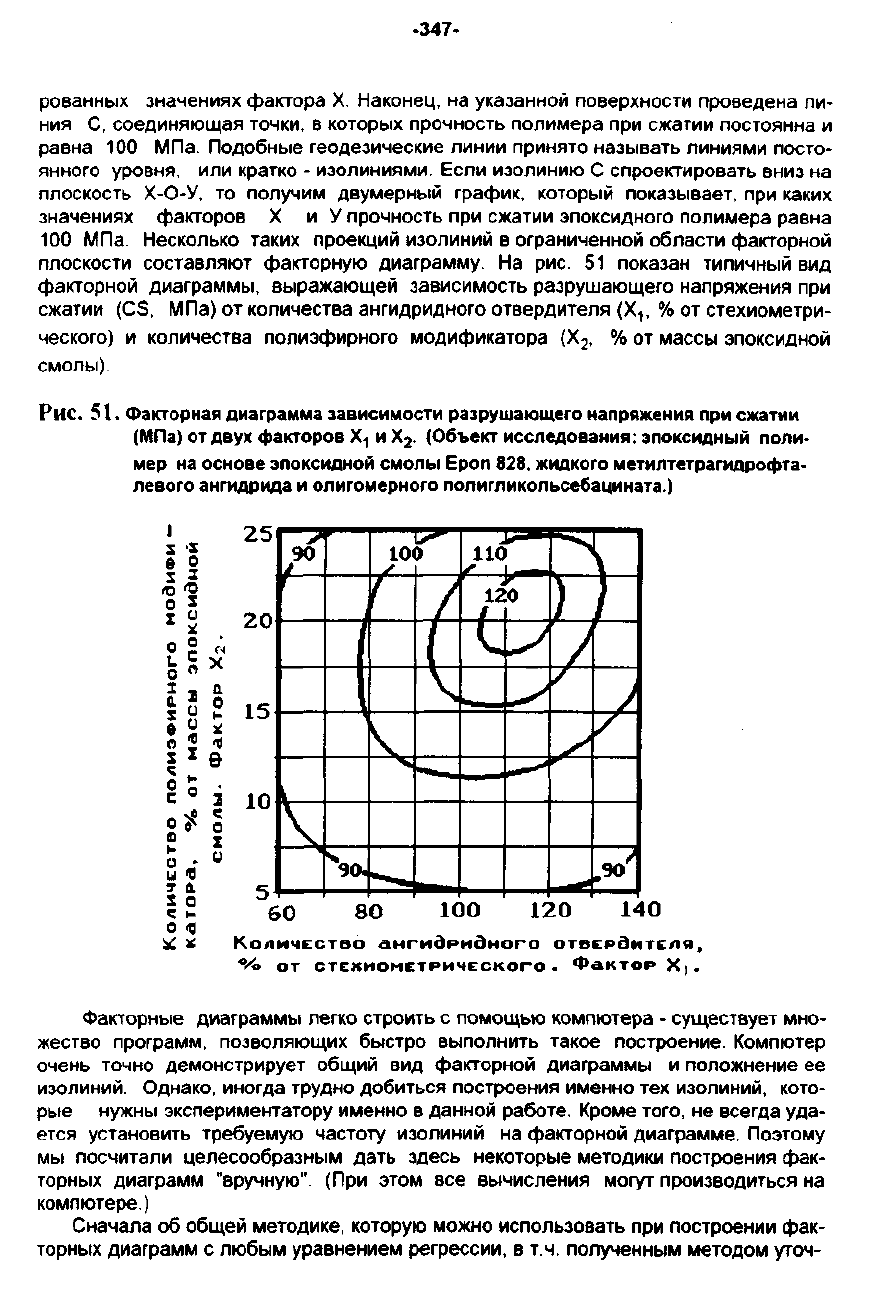
На
рис.
51
показан
ТИПИЧНЫЙ
ВИД
факторной
диаграммы,
выражающей
зависимость
разрушающего
напряжения
при
сжатии
(СЗ,
МПа)
от
количества
ангидридного
отвердителя
(Х
1
.
%
от
стехиометри
ческоro)
И
количества
полиэфирного
модификатора
(Х
2
•
%
от
массы
эпоксидной
смолы).
Рис.
5 t.
ФаКfорная
диаграмма
зависимости
разруwающего
напряжеНИА
при
сжатии
(МПа)
от
двух
факторов
Х
1
и
Х
2
.
(Объект
исследоваНИА:
,поксидный
поли
мер
на
основе
,поксидной
смолы
Ероп
828,
жидкого
меТМIIтетрагмдрофта
левого
ангидрида
и
олигомерного
полигликольсебацината.)
I
·
'.
•
о
· :
",,,,
о
•
1 "
. ,
о о
(~
СОХ
о"
: , .
• "
о
• "
>-
•
••
~
1 :
•
>-
о о
'
о
]
~
*
~
>-
1
" . "
" .
• •
•
о
•
>-
о.
".
25
90
20
15
10
I\.
5
60
10~
;'
"
"9~
80
1)10
"""'\
/
}ZO
J
\..
~
/
"
.,.
./
/
90'
100
120
140
КОАИЧЕСТВО
ангидридного
ОТВЕРдИТЕАQ.
О/О
от
СТЕХИОМЕТРИЧЕСКОГО
_
Фактор
х,_
Факторные
диаграммы
леfl(О
строить
с
помощью
компютера
-
существует
МНО
жество
программ,
позволяющих
быстро
выполнить
такое
построение.
Компютер
очень
точно
демонстрирует
общий
вид
факторной
диаграммы
и
положнение
ее
изолиний.
Однако,
иногда
трудно
добиться
построения
именно
тех
изолиний,
кото
рые нужны
экспериментатору
именно
в
данной
работе.
Кроме
того,
не
всегда
уда
ется
установить
требуемую
частоту
изолиний
на
факторной
диаграмме,
Поэтому
мы
посчитали
целесообразным
дать
эдесь
некоторые
методики
построения
фак
торных
диаграмм
"вручную"
(При
этом
все
вычисления
MOryт
производиться
на
компютере.
)
Сначала
об
общей
методике,
которую
можно
использовать
при построении фак
торных
диаграмм
с
любым
уравнением
регрессии,
в
Т.Ч,
полученным
методом
yrоч-

нения
вогнутости
поверхности
отклика,
методом
преобразования
целевого
пара
метра
и
др.
Для
начала
разберем
методику
построения
факторной
диаграммы
на
примере
двухфакторной
модели.
8
дальнейшем
будет
показано,
что
такое
постро
ение
с
некоторыми
ограничениями
можно
осуществить
и в
случае
многомерных
уравнений
регрессии.
Допустим,
что
зависимость на
рис.
51
адекватно
описывается
уравнением
рег
рессии
типа
(24).
Такое
уравнение
регрессии
можно
преобразовать
к
виду:
Схема
46:
Z
=
(С,СЗ)
+
(С2СЗ)Ч
+
(а22
с,)ч
2
+
(аZZС2)Х2З'
где
с.
=
(Ь
О
+
Ь.х.>;
С:
=
(Ь
:
+
ыz');;
С)
=
("о
+
аIlЧ
Z
).
При
постоянных
значениях
фактора
Х
1
(имеются
ввиду
кодированные
значения
этого
фактора)
-
это
уравнение
кубической
пораболы,
с
помощью
которого
легко
рассчитать
и
построить
график
зависимости
Z = F(X
2
).
Таким
способом
рассчиты
вают
несколько
графиков
при
фиксированных
значениях
Х
1
,
так
чтобы
они
отража
ЛИ
одномерные
сечения
над
всей
поверхностью
отклика
и
далее,
с
использованием
этих
графиков,
строят
факторную
диаграмму.
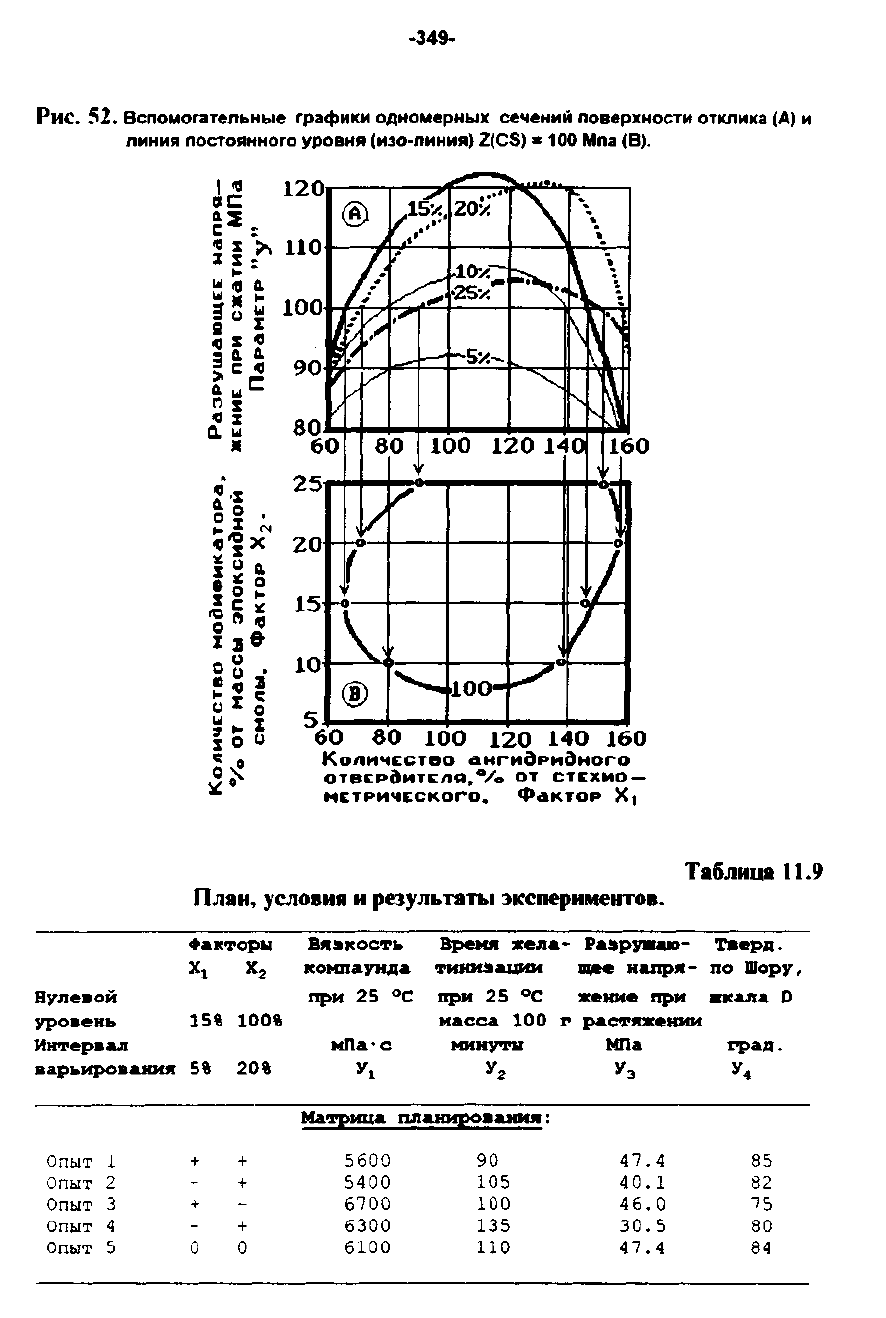
Техника построения
факторной
диаг
раммы
весьма
проста
и
для
изолинии
Z = 100
МПа
показана
на
рис.
52.
Если
адекватной
моделью
экспериментальной
зависимости является
непол
ное,
или
полное
квадратное
уравнение,
то
построение
факторной
диаграммы
мож
но
выполнить
более
простным
методом.
Координаты
факторов,
соответствующие
заданному
значению
параметра
Z,
можно
рассчитать
сразу,
не
выполняя
nocтрое
ния
вспомогательных
одномерных
сечений.
В
случае
неполного
квадратного
урав
нения
нужно
воспольэоваться
формулой
(47):
Z -
Ь
о
-
btXt
Ь
2
+
Ь.12
Х
l
Схема
47:
Если
модель
-
полное
квадратное
уравнение,
то
для
pa~eTOB
подходит
следую
щая
формула:
Схем.
48:
• •
!>иХ,
-
z>
где
Z -
заданное
значение
параметра
(на
рис.
52 Z = 100
МПа).
Сейчас
подошло
время
объяснить,
для
чerо
необходимо
выполнять
такие
слож
ные
построения
факторных
диаграмм.
Как
обычно
мы
это
сделаем,
рассмотрев
простой
пример.
П
р к
м
•
р.
изучали
свойства
ЭПОКСИДного
полимера
на
основе
ненаnoлненной
элоксидной
смолы
типа
Ерon
828,
аминнorо
отвердителя
и
разбавителя. Разба
витель
вводили
в
состав
отвердителя.
Похаэателями
качества
технического
реше
ния
являлись
вязкость
И
время
желатинизации
компаунда,
разрушающее
напря
жение
полимера
при
растяжении
и его
твердость.
Изучали
влияние
концентрации
разбавитепя
(Х"
%
от
массы
зпоксидной
смолы)
И
количество
немоДИФицирован
ного
отвердителя
(%
от
стехиометрического)
на
указанные
параметры.
План,
усло
вия
и
результаты
экспериментов
даны
в
таблице
11.9.
·349-
Рис.
52.
Вспомогатеn"ные
графики
одномерных
сечен
..
"
поверхности
отклиn
(А)
н
пмния
постоянного
УРОВНЯ
(И30-ПННИЯ)
Z(CS).
100
Мпа
(В).
Нуле.оЙ
ура.ень
ИН'l'ераa.n:
.ар
..
мроа&ЮUI
Опыт
1
ОПЫТ
2
Опыт
3
Опыт
4
Опыт
5
'"
.с
O~
с ,
".
~
•
••
• •
• "
о
• ••
" u •
• •
•
••
3
о о
>
с
•
О.С
о.
• •
0..
•
®
.;;:::
,\'\,
:
......
",
1;
/.
"
90И;
:.-
--
"n
б
,
О
100
1:~0
1·
;о
;'
v
f/
'\..
®
,
......
"."
"
19
~O
1(10 1
1.!0
160
КОnИЧЕстео
ОТ8ЕРС)МТЕnЙ:О;~
НЕтричltскоrо.
Таблица
11.9
План~
услоаии
и
результаты
эксперимеНТО8.
•
aKTopIoI
BflSllCoc'I'J.
ВPeМR
zena-
Pa~pV8aD-
Т8ер,А
.
Х,
Х,
lCoмnaVНд&
--
...
нanp"-
ПО
Шору,
при
2S
ос
при
25
ос
-
....
-
..
ал.
D
15% 100%
масса
100
r
ра
........
нии
мп.·с
ми
.......
МN.
rpaoA.
5%
200
У,
У, У,
У,
матрица
nЛ!lDfPO
.....
:
+ +
5600
90
47.4
85
+
5400
105
4
0.1
82
+
6700
100
46.0
'5
+
6300
135
30.5
80
О
О
6100
110
47.4
84
·350-
При
обработке
резуль
татов
этого
эксперимента
был
использован
метод
уточ
нения
вогнутости
повеРХНОСТИ
отклика,
что
дало
следующие
адекватные
уравнения
регрессии:
Схема
49:
У(
= (6000 +
'50Х(
-
5ООч
-
5ОХ(ч)(I.ОI7
-
0.0О9Х(1_0.008ч2)
У
1 =
(I07.5-12.5х(-1O.0ч+
5
•
Ох
(ч)(1.02З-О.ОI4х
(1-О·00912)
Уз
= (41.0 +
5.7Х(
+
2.8Оч
-
2.0Х(ч)(I.I56
-
0.I05x(1-
О.О5Оч2)
У
4 = (80.5 -
0.5Х(
+
3.0ч
+
2.0Х(ч)(l.043
-
0.ОО6х(1
-
0.037ч2)
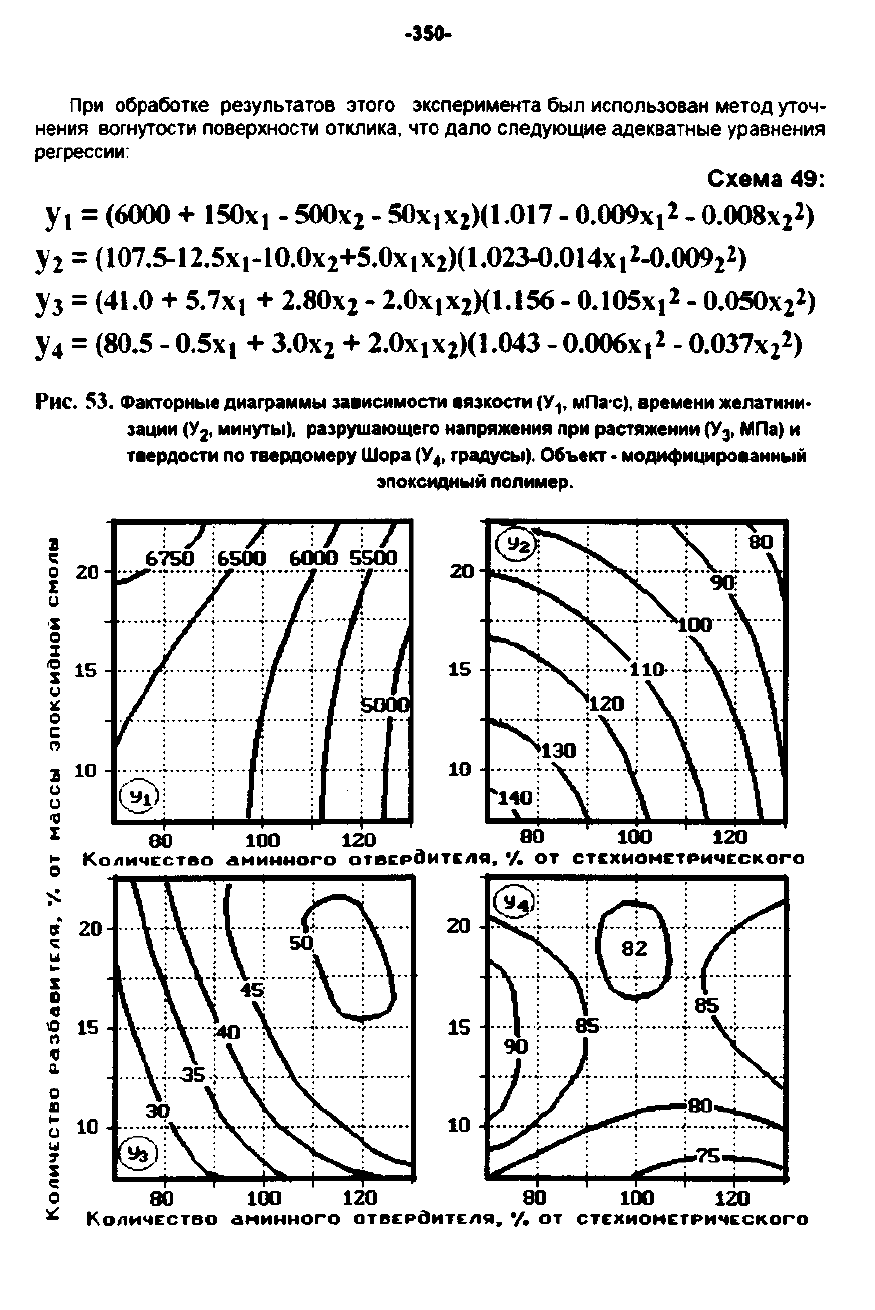
Рис.
53.
Факторн
....
диаграммы
,.8ИСИМОСТИ
8t13KOCТМ
(У
l'
..
Па'с),
времени
желатини,
зацми
(У2'
минуть.),
разpywающеro
напряжени"
при
растяжени"
(уз.
МП.)
н
,
••
рдости по
твердом.ру
Шора
(У
••
rpaдy<:bl).
06ъект·
мОДМФмцмроuннwй
:SПОКСМДНWЙ
поnимер.
•
•
о
20
•
"
'.
о
,
'"
15
•
"
"
о
"
•
•
10
"
"
•
•
6750
i
6sOO
6000
ssoo
••
~
0.0
••••
~.
•
•••
~
••
0.0..
•
•••••
-:-
••••••
20
·······i···
.':'
......
~.
0.0
•
-t
.....
:
....
0.0
15
•••
о
•••••••••
_.,_
••
_.
,_
10
во
100 120
80
100 120
~
КОЛИЧЕСТВО
4НИММОГО
ОТ8ЕраИТЕn~.V.
от
СТЕХИОНЕТРИЧЕСКОГО
О
ri
20
•
"
-
•
•
•
>о
15
•
•
•
о
•
~
10
"
•
•
•
о
20
15
10
.-.._..,'80
'
,
~,_.(
....
: .... _ .. ~_
.......
~_
..
.
во
100 120
80
100
120
"
КОI1ИЧЕСТВО
4"инноrо
ОТ8ЕраИТЕnЯ~
0'0
от
СТЕХМОНЕТРМЧЕскоrо
