Мордухай-Болтовской Д.Д. Философия, психология, математика
Подождите немного. Документ загружается.


Берем его наиболее примитивную форму, которая находится у
Кеплера.
Для определения площади д
иавливает перпендикуляр ВС = OA
1
'
и откладывает ВВ, = AA
t
, B
(
B, = АА,и т.д. В силу равновеликое™ треу-
гольников А,А
2
С,, BBjC, и т.д. он полагает, что площадь круга равна сум-
ме площадей треугольников В
и
_. СВ
я
= ВСР, т.е. теорему Архимеда.
В этом рассуждении признается существование актуально-беско-
нечно малых элементов круга, и при этом признается, что те признай!
двух элементов, об уменьшении разности которых свидетельствует интуи-
ция,
для бесконечно малых элементов совершенно сравниваются.
Это доказательство прямое в противоположность апагогическому
методу
1
исчерпывания.
На это следует обратить внимание. Вне сомнения, в дальнейшем
при нападках рационалистов на апагогические доказательства
25
развитию
метода неделимых способствует не столько его простота и практичность,
как прямой характер его выводов.
В дальнейшем у Кавальери косвенная схема метода исчерпывания
превращается в более простую схему метода исчерпывания.
Чтобы доказать, что
А
:
В = а
:
Ь,
А и В разбиваются, согласно идее второго метода Архимеда, на
части, причем неделимые части (такое понятие, конечно, чуждо Архиме-
ду)
круга Кеплер делит круг радиуса-
ми на равные бесконечно малые
секторы (черт, 1). Эти бесконечно
малые секторы он признает тожде-
ственными бесконечно малым тре-
угольникам с высотой, равной ра-
диусу, и основанием, равным дуге
сектора К. К прямой РВ он восста-
С
Р
В
3
В
2
В Q
Доказывается, что для всякого.)
<Xj:
Pj = a:b
путем отождествления
ajHPj,
<*jH
pj
для которых не трудно установить пропорцию
ocj :pj = a:b
222

Легко видеть, какому изменению подвергается эта схема при уста-
новке понятия бесконечно малого в современном смысле - как переменно-
го с пределом = 0.
Имеем, А = lim ^ а •, В = lim £ р у Далее, a
j,
р j
не тождествен-
иы
ъ
а только эквивалентны
26
, ctj и pj т,е, lim
а
>
lim = 1, поэтому
на основании второй леммы анализа
A = lim£aj B = lim£pj ,
а так гак a
j:
(jj = a
:
b, то
A
:
В = a
:
b.
Сточки зрения Кавальер и ctj и Pj суть не эквиваленты частей А и
В,
а суть сами эти части, А и В - не пределы суммы, а сами суммы a
j
и
Р j
или,
что то же и р\.
Отсюда вытекает принцип Кавальери
27
, устанавливающий равен-
ство величин из равенства их неделимых, равенство двух тел между двумя
параллельными плоскостями из равенства площадей их сечений параллель-
ными этим плоскостям плоскостями и т.д.
Этот метод совершенно чужд античной мысли.
Торичелли
28
старается убедить в том, что метод неделимых слу-
жил у античных математиков методом открытия, который не совпадал с
методом доказательств, но с этим едва ли можно согласиться.
В действительности же психология открытий тех теорем, которые
доказывались Евклидом и Архимедом апагогическим путем, много про-
ще,
чем думал Торичелли. 2-е полол<ение XII книги "Начал" - естествен-
ное распространение того, что уже доказано для подобных прямолиней-
ных фигур и вообще подобных фигур. Таково же происхождение и 18-го
положения XII книги.
Теорема Архимеда о площади круга составлена по образцу тео-
рем,
относящихся к площадям правильных многоугольников. Значения по-
верхностен и объемов конусов и цилиндров верней всего были найдены
развертыванием их в плоскости, что, конечно, проще метода неделимых.
Совершенно невероятно, чтобы этот метод, совершенно неудобный
при нахождении объема и поверхности сферы, применялся Архимедом в
этих случаях как эвристический.
Впрочем, сам Архимед в упомянутом выше сочинении совершен-
но ясно говорит об истории своих открытий. Аналогон круга - сфера, тре-
223

угольника - конус. Вот эта мысль и руководит Архимедом в поисках выво-
да,
конечно ощупью, формулы для объема шара.
Архимед
19
говорит: "Благодаря изложенной теории о том, что шар
в четыре раза больше конуса, которого основанием служит большой круг, а
высота равна радиусу круга, мне пришла в голову мысль, что поверхность
шара в четыре раза больше его большого круга, причем я исходил из пред-
ставления, что как круг равен треугольнику, основанием которого служит
периферия круга, а высота равна радиусу круга, так и шар равен конусу,
которого основанием служит поверхность шара, а высота равна радиусу
этого шара".
В сочинении "О шаре и цилиндре" Архимед строит строгое дока-
зательство (причем апагогнчески) этих положений.
Аналогон параболы - параболоид (коноид) и теоремы об объеме
сегмента коноида - аналогон раньше открытой теоремы о площади пара-
болического сегмента.
Теорема о сфероидах - естественное обобщение теоремы о сфере.
§
б.
Третья архимедова форма метода исчерпывания.
В третьем методе Архимедова неравенства. (5) заменяются:
р
<•">
< А
р « < в.
ь
То,
что А - Р
а
<'"> может быть сделано как угодно мало, выясняется
построением.
Р образуется из частей, каждая последующая из которых полу-
чается из предыдущей делением последней по определенному закону;
Р
1
(Ш,
= Р
11
+Р, +...Р,
P
n
> Р, > Р„ >...>Р, ,
Дальше доказывается, что при взятии достаточного числа членов
P
aj
-разность В - Р
а
(п1)
может быть тоже сделана сколь угодно малой. Невоз-
можно, чтобы А < В, ибо тогда
В-Р
Л
Ы
>В-А
я невозможно, чтобы А > В, ибо тогда
А-Р
а
(
"° >А-В.
В известном выводе Архимеда площади сегмента параболы за Р
а|
принимается площадь Д АОВ, вписанного в сегмент, за Р
]2
- Д OFB, вер-
шина F которого на FM J. АВ и МС = MB и другого аналогичного треуголь-
ника, за Р
а3
- Д FHB, где HN 1 СВ и MN = NB и других аналогичных тре-
угольников и т.д.
224

К этой форме больше всего
подходит название "метод исчер-
пывания'". А
Представление Р
о
<
т
> суммой
2^P
a
j
представляет ие что иное,
как приближенное вычисление Р
а
(т
>,
Берется величина Р
п1
близ-
ки!
кР^"
0
, которая может быть при-
знана за первое ее приближение.
Это будет то, что можно назвать
первым черпком. Затем берут оста-
ток Р./
1
"' -Р
а1
и ищут его прибли-
жение Р „.
П*
Это будет второй черпок. Рассматривая новый остаток - Р
а]
-
Р
я1
, находим его приближение Р
Л
и т.д. С некоторым черпком
Р
я
<л,
>
оконча-
тельно исчерпывается, получается полное значение.
Но те же черпки служат и для приближенного вычисления А, но
здесь точное значение уже ие достигается. Внося идею предела, можно ска-
зать,
что предел суммы таких черпков будет точно равняться исчерпывае-
мой величине А, которая, таким образом, является пределом суммы беско-
нечно великого числа слагаемых, бесконечно убывающих, начиная с пер-
вого.
Чтобы выявить, каким образом эта форма приводит к этой другой
точке зрения анализа, рождающей на ряду с интегралом еще ряды, мы пред-
ставим способ Архимеда определения площади сегмента параболы
в
пере-
работанном виде с привлечением понятия предела. Первое приближение
(черт. 2) площадей, вписанных в параболу у
2
= х Д АОВ (ВС=1, ОС=1), т.е.
1.
Остаток - площадь сегментов АО и ВО.
Приближение их - площадь треугольников, в них вписанных. Удоб-
нее всего брать OFB, где Е середина СВ и EF || OY
IE ОЕ 1 1 " I
=
ДЕ
=
—.
К
ОС
(как у пр
и
х =
KF
= FE=—) равняется—
ВС ОВ 2 2 4
Bl
=
iS2,KL=-!-,LF=KF-KL=ffi-KL=-!—!-=-
ВС ОС 4 2 4 4
пл.
OBF и
-гг-~-=—, как высоты, опущенные на общую сторону ОВ. но после-
пл.ОВС а
дние относятся как параллельные отрезки LF = ВС, т.е. как 1:4.
225
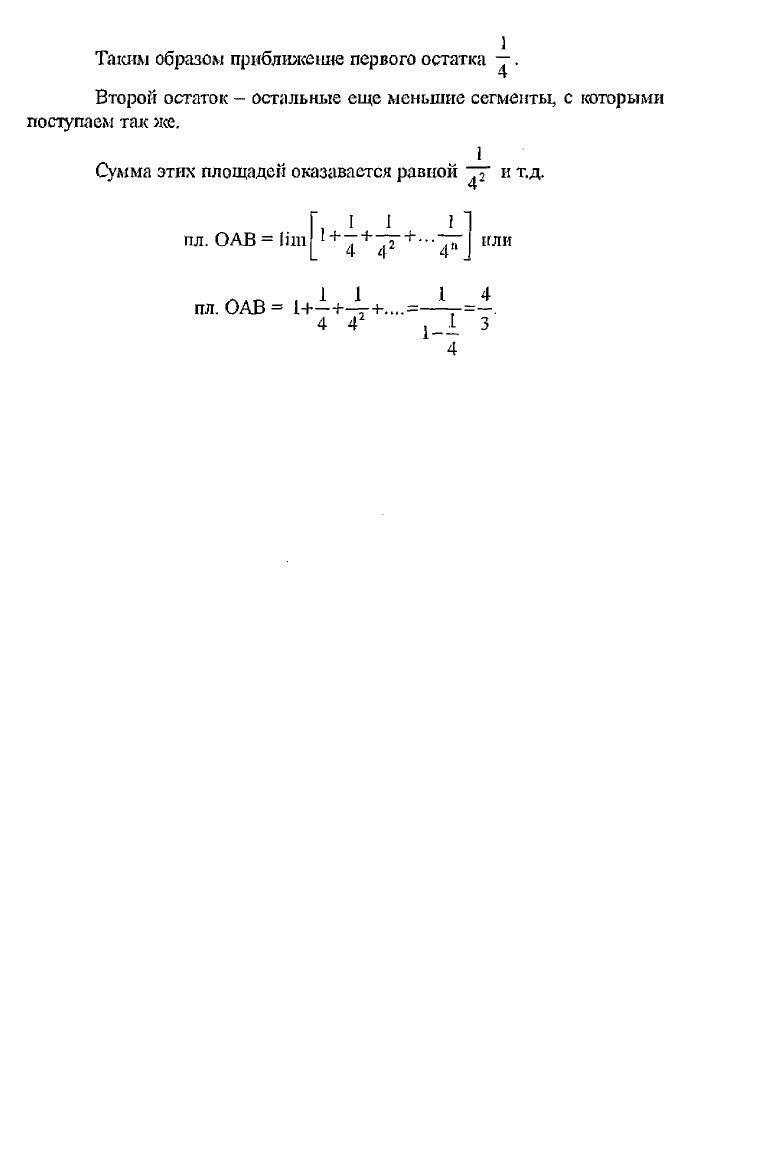
1
пл.
ОАВ = lim
, I I
4 4 ' 4" J
или
пл.
ОАВ = 1+—+Д-+....=—
4 4
Z
Таким образом приближение первого остатка —.
Второй остаток - остальные еще меньшие сегменты, с которыми
поступаем так же.
1
Сумма этих площадей оказавается равной и т.д.

ИЗ ИСТОРИИ МЕТОДА НАЛОЖЕНИЯ
В ЭЛЕМЕНТАРНОЙ ГЕОМЕТРИИ
,S
1. Евклид и Лежандр.
Элементарный учебник геометрии в большей или меньшей мере представ-
ляет из себя методическую переработку евклидовых "Начал"
1
, правда, по-
полненных некототрым новым материалом. Можно сказать, что изучение
геометрии мы начинаем с Евклида. Но только этому положению следует
придавать правильный смысл. Верно то, что мы изучаем те теоремы, что
большей частью находятся у Евклида, но если глубже вникнуть в евклидо-
вы "Начала", то увидим, что мы далеко отошли от них в самом существен-
ном,
в понимании основной проблемы - доказательства выставляемых по-
ложений, образующих систему геометрии.
Понятие о сущности математического доказательства, подверглось
через толщу веков глубочайшему изменению, хотя это изменение и ие было
заметно самим исследователям так, как не заметно старение стареющему
человеку. То. что Лежандр считает доказательством, не могло быть при-
знано за доказательство Евклидом и, с другой стороны, Лежандр ие мог
начать свои "Элементы" с построения равностороннего треугольника, как
это делает Евклид.
Не следует думать, что Лежандр
2
в своих упрощенных доказатель-
ствах додумался до тех более простых доказательств, которые ускользнули
от Евклида. Евклид, очень может быть, знал эти доказательства, но отверг
их как негодные, как находящиеся в решительном противоречии с его взгля-
дами на доказательство. Почему ему не поступать так, как Лежандр, при
доказательстве основного свойства равнобедренного треугольника, состоя-
щего в том, что углы, противолежащие равным сторонам, равны?
Ведь, кажется, нет ничего проще, как соединить середину стороны
BC-D с вершиной А и доказать на основании третьего случая конгруэнтно-
сти равенство треугольников ABD и
ADC*,
Между тем, Евклид излагает другое, более сложное доказатель-
ство (так называемое elefuga). Ответим: потому, что Евклид признавал су-
ществование только тех объектов, которые могут быть построены.
Он потребовал бы от Лежандра указать построение точки D - се-
редины отрезка. ВС. Но построение это (предл. X, 1 книги) основывается
на 9-м положении о делении угла на две равные части, последнее же - на
третьем случае конгруэнтности, а третий случай конгруэнтности доказы-
вается от противного на основании 7-го положения'
1
.
"Если мы соединим концы основания АВ с двумя точками С и D,
лежащими по одну сторону прямой АВ, то расстояния СА и СВ точки С от
227

Черт. 1.
концов основания АВ не могут быть равны гаждое каждому расстояниям
DA и DB от тех же концов АВ".
Для доказательства невозможности
единовременного существования равенств
AC=AD, DB=BC Евклид (черт. 1), пользу-
ясь elefuga, доказывает, что ZADC=Z ACD
н вторично применяя elefuga, что
ZCDB=ZDCB, обнаруживает несовмест-
ность этих двух равенств углов, так как Z ADC>Z CDB и ZBCD Z ACD
(мы берем только тот случай, когда D вне ABC).
И только благодаря коренному изменению требований, предъявля-
емых к доказательству, Лежандр получает возможность упростить гео-
метрическую систему и перевернуть порядок теорем.
Он начинает с положения:
"Если две стороны одного треугольника равны соответственно сто-
ронам другого и если в то же время угол между первыми более угла, зак-
люченного между вторыми, то третья сторона первого будет больше тре-
тьей стороны второго".
Но это только 24-я теорема I книги "Начал" Евклида, т.е. весьма
отдаленная от начала теорема, которая доказывается на основании третье-
го случая кощруэнтности треугольников.
Для доказательства того, что
при
AB=FG ]
АС
= GH I
также
HBC>FH
ZBAC>ZFGH]
Лежандр
3
, отклады-
вая (черт. 2) угол ZCAD =
ZFGH
II
AD=FG строит треу-
гольник CAD, равный FGH
(на основании 1 случая конг-
руэнтности), проводит биссек-
трису АЕ угла BAD и соеди- /\
няет Е с D и доказывает ра-
венство треугольников ВАЕ и
EAD CD < ED + ЕС, откуда CD < ВЕ+ЕС, CD < ВС или FH < ВС.
Эта теорма дает сейчас же возможность вывести (апагогически)
третий случай конгруэнтности.
Доказательство это, конечно, не моо/сет быть принято Евклидом,
ибо построение биссектрисы является необоснованным.
Черт. 2.
228

Античное доказательство вовсе не чисто логическое. Античный
математик убеждает не одним силлогизмом, но и актом, вычерчивающим
геометрическую фигуру.
Выражения Аристотеля* очень напоминают Шопенгауэра
7
. Соглас-
но Аристотелю, свойства геометрических фигур открываются приведени-
ем к актуальному существованию геометрической фигуры, вызывающим
разложение данных фигур. Если фигуры уже даны разложением, то свой-
ство уже очевидно, оно просто видно глазу. Но если они не разложены, то
находятся только в потенции (лучше было бы сказать - их знание в потен-
ции).
Почему сумма углов треугольника равна двум прямым?
Потому, что сумма углов, образованных около данной точки на од-
ной линии, равна двум прямым углам. Если образовать внешний угол, про-
должая стороны треугольника, непосредственное доказательство очевид-
но.
Почему угол, вписанный в полуокружность, неизменно прямой? Это
потому, что имеет место равенство для трех линий: двух половин основа-
ния и прямой, проведенной от центра круга к вершине угла, противолежа-
щего основанию: это то равенство, которое дает возможность познать свой-
ство вписанного угла
8
.
§
2.
Постулаты.
Евклид, как и Аристотель, не задавался целью вывести все свои положе-
ния силлогистически из немногих высказанных им определений, постула-
тов и аксиом. Его целью было лишь убедить читателя в определенных ис-
тинах, но он вовсе не считал единственным способом убеждения формаль-
но-логический вывод положений из признанных читателем в начале ис-
тин.
Очевидность (lux liaturale, естественный свет) только рационалиста-
ми"
XVII века вполне определенно признана за критерий истинности поло-
жений, в аристотелевской же логике
10
она ие играет этой роли.
За правильность предпосылок, с которых начинается цепь доказа-
тельств, говорит скорее общее их признание, вследствие чего аксиомы и
называются %oivou8vvoiai (communes rationes). Доказательства Евклида
вполне отвечают схемам, выработанным софистикой.
В начале следует привести противника к признанию некоторых
положений, отнюдь не апеллируя к очевидности, ибо противник мог бы
поднять вопрос об относительности понятия очевидности и признать для
себя не очевидным то, что для противника - является вполне очевидным.
Более сильным фактором являлась общепризнанность необходи-
мых для дальнейшего положений, необходимость противнику при их отри-
цании его встать в смешное положение. Отсюда стягивание аксиом к нача-
лу сочинения.
229

Но что такое постулаты, выставленные Евклидом тоже в начале
сочинения наряду с аксиомами".
Неправильно относить к аксиомам очевидные положения общего
характера, т.е. положения, относящиеся к величинам вообще, а не только к
геометрическим, какова, например, первая евклидова аксиома: "величи-
ны,
равные одной и той лее, равны между собой", и отождествлять постула-
ты
12
с геометрическими аксиомами. 11-я аксиома фигурирует иногда 5-м
постулатом, а 10-я (о равенстве прямых углов) 4-м, но 12-я (две прямые
линии не заключают пространства) и 8-я (о равенстве совпадающих при
наложении фигур) - всегда аксиомы.
Только отказавшись от проектирования в прошлое современных
формально-логических тенденций, мы будем в состоянии понять, что пред-
ставляют для Евклида постулаты. Евклид геометрическим объектам вовсе
не приписывает идеального существования. Доказывающий какую-либо
теорему сам вызывал к существованию геометрическую фигур}', с какового
момента она и начинала свое существование.
Признание возможности существования прямой, круга и т
;
д. явля-
лось равносильным признанию акта, их производящего, что и представля-
ет содержание постулата
13
. Более того, признание этого акта вынуждало
признание некоторых истин, например, признание третьим постулатом воз-
можности описания кругов вызывало признание пересекаемости кругов,
проходящих, через центры друг друга
Следующее объяснение дает Геиинус
14
, согласное с нашим. "По-
стулат, - говорит
он,
- представляет требование найти или сделать (fabricari)
то,
что достигается просто и непосредственно, в чем ум не затрудняется ни
в понимании, ни в построении".
Прокл, говоря о различии теорем и проблем и отмечая, что цель
первых - познать, вторых - сделать, приводит в соответствие с первыми
аксиомы, со вторыми постулаты, определяя последние близко к Геминусу.
Гоббс
15
вполне ясно выражает нашу мысль. То, что называется постулата-
ми,
это истинные принципы, но не доказательства, а построения поэтому
не знания, а потенции.
§
3.
Метод наложения у Евклида.
Большим диссонансом с общими тенденциями "Начал" представляется
метод наложения при доказательстве первого случая равенства треуголь-
ников, если этот метод понимать так, гак мы обычно его понимаем.
Здесь не мы имеем идеальное существование начерченных геомет-
рических фигур с идеальным их перенесением с одного места на другое,
[как обычно считают].
Но мне представляется, что как мы, так и целый ряд предшествую-
щих поколений, совершенно неправильно здесь понимают Евклида.
230

Положения 2 и 3, предшествующие положению, доказываемому
наложением, наводят на мысль, что сам Евклид здесь вовсе не разумеет
наложение в нашем лежандровом смысле.
Положение 2-е:
10
Из данной точки А провести прямую, равную
данной прямой ВС.
Почем)' Евклид не делает так, как мы делаем и как рекомендовали
это делать некоторые авторы XVII века
17
: проведя через А какую-нибудь
прямую, не переносят в нашем смысле отрезок ВС?
Почему он не может сделать с одним отрезком то, что в четвертом
положении он делает с целым треугольником'!
Отвечу: потому что он ие признает в нашем смысле перенесения,
потому что то, что мы считаем перенесением идеального треугольника, -
для него является построением тождественного данному треугольника
о ином месте, чем он задан.
Евклид строит на АВ, на основании первой теоремы "Начал", рав-
носторонний треугольник ABD, из В описывает радиусом ВС окружность
до пересечения с b в G; из D описывает радиусом DG окружность до пере-
сечения с AD в К. Если бы мы желали "перенести" ВС на определенную
прямую AL, проходящую через L, то пришлось бы описать еще третью
окружность радиусом АК до пересечения с AL в L (согласно предл. 3) .
Наложение DEF на АБС представляет:
1) построение на АВ отрезка, равного DE, начиная с А,
2) проведение другой прямой под тем же наклонением к АВ, что
АС (согласно 8-му определению - угла), откуда следует, что DF пойдет по
АС и
3) построение отрезка, равного DF на АС. откуда следует, что F
совпадет с С. Легко видеть, что в этот момент, т.е. при заключении, что
соединение точек Е и F прямой, т.е. построение третьей стороны EF дает
АВ,
должен возникнуть скачок. Софист возразит: "Я позволил от одной
точки к другой провести прямую, но откуда мы знаем, что в одном случае
получится одна, а в другом опять та же прямая'?". Здесь становится необхо-
димым подчеркнуть еще одйо общепризнанное положение - 12-ю аксио-
му: "Две прямые не могут заключать пространства"".
Идеальное существование геометрических объектов - плод схола-
стического реализма
29
. Такое существование за ними закрепилось и в ма-
тематической мысли XVI века. Математик XVI века понимает наложение
уже в нашем смысле и обнаруживает тенденцию пользоваться им шире,
чем Евклид.
У Клавия мы находим разновидность этого метода, чуждую Евк-
лиду.
Верный духу своего времени, Клавий
2
' заменяет косвенное дока-
зательство теоремы 6 1-й книги (обратной elefuga) прямым наложением
Д АСВ на Д ABC (ZB = ZC), так. что треугольник подвергается мыслен-
231
