Миллер Р.Л., Ван-Хуз Д.Д. Современные деньги и банковское дело

Подождите немного. Документ загружается.

366 ЧАСТЬ IV Операции центрального банка; денежно-кредитная политика

и Федеральная резервная система

уравнение (14-18) для нахождения денежного мультипликатора в экономике. Тогда

если бы мы работали на ФРС в качестве экономистов, то смогли бы дать рекомен-

дации, какой должна быть денежная база для обеспечения определенной денежной

массы в экономике.

Эта модель хороша по двум причинам. Во-первых, она проста для понимания, если

вы усвоите вывод уравнения (14-18), а у вас будет возможность получить такого рода

практические навыки, выполнив задания в конце главы. Во-вторых, для расчета де-

нежного мультипликатора не нужен большой объем информации.

Однако следует подчеркнуть, что у модели денежного мультипликатора есть неко-

торые ограничения. Довольно соблазнительно рассматривать денежный мультиплика-

тор m = (1 + c)/{d

Л-

е + с) как постоянную величину, но это далеко не так. Только

требуемая норма резервного покрытия d приблизительно постоянна, хотя она может

немного различаться, поскольку на практике норма, например, для первых 42,2 млн.

долл. депозитов в любом банке равна 3%, а для депозитов, превышающих эту сум-

му, — уже 10%.

Значения других переменных {е и с) полностью зависят от поведения банковской

системы и небанковского сектора соответственно. Если банки становятся более «кон-

сервативными» (возможно, они ожидают спада в экономике), то величина е может

увеличиваться, вследствие чего денежный мультипликатор будет меньше. То же самое,

если небанковский сектор будет снимать больше наличных денег со счетов при потере

доверия к стабильности банковской системы, и значение с станет больше. (Так, в

нашем примере денежный мультипликатор равен 3,125 при с = 0,25. Если с увели-

чится до 0,30, тогда новое значение денежного мультипликатора будет: (1 + 0,30)/

(0,10 + 0,05 + 0,30) = (1,30)7(0,45) = 2,889, что, естественно, меньше, чем 3,125.)

Эмпирические расчеты денежного мультипликатора Поскольку компоненты фор-

мулы денежного мультипликатора меняются в зависимости от поведения банковской

системы и небанковского сектора, нельзя точно знать, каким же будет денежный

мультипликатор в различные периоды.

Экономисты могут с точностью вычислить денежные мультипликаторы прошлых

периодов с помощью отношения денежной массы (денежные агрегаты Ml и М2) к

денежной базе {MB) или используя суммарные резервы депозитных учреждений ( 77?)

плюс наличность (С), которые и составляют денежную массу. Таким образом.

Ml М2

' MB ' MB

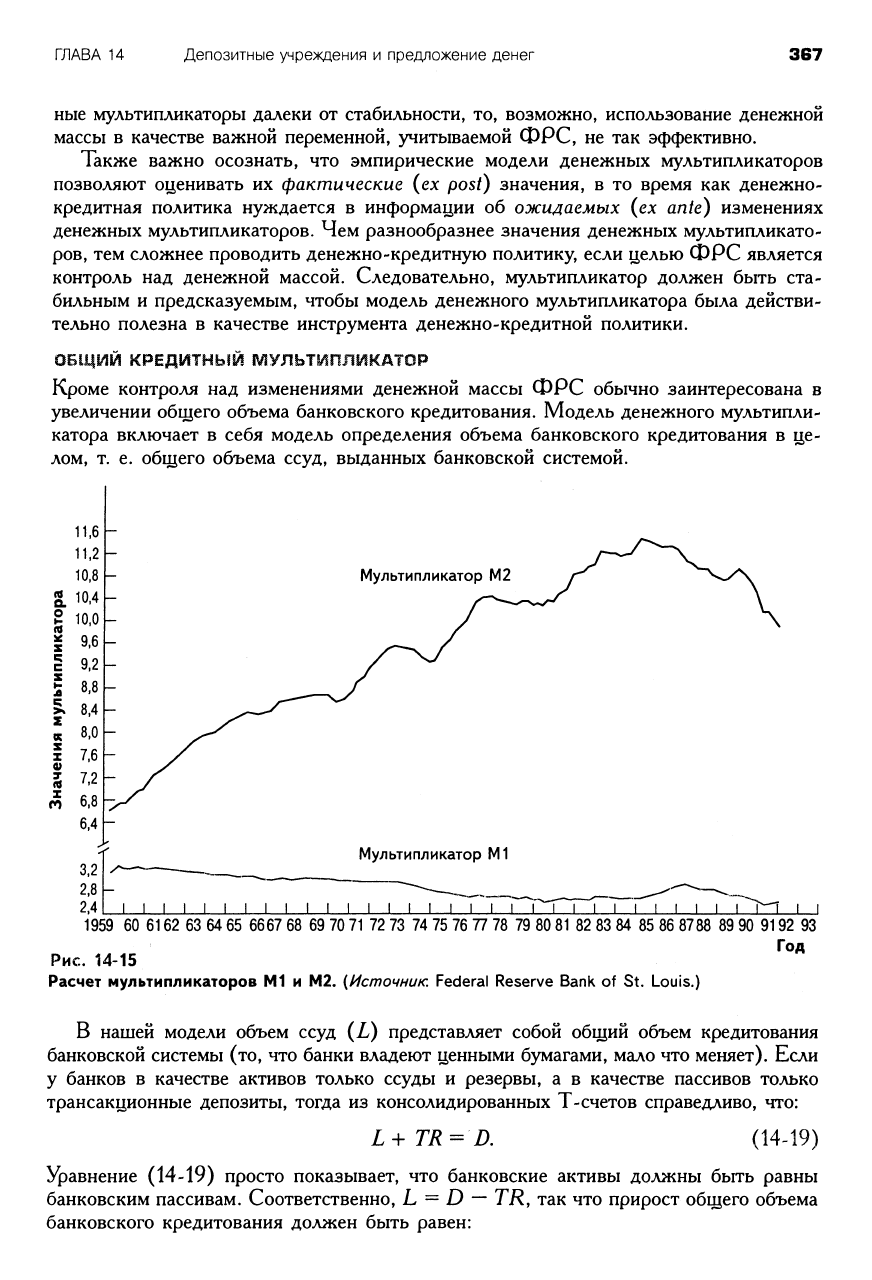
На рис. 14-15 показаны эмпирические расчеты денежных мультипликаторов Ml и

М2 с 1959 по 1992 г. Как и ожидалось, мультипликатор М2 больше мультипликато-

ра Ml (у него больший числитель при одинаковых знаменателях); мультипликатор М2

постепенно растет, в то время как мультипликатор Ml более стабилен.

Отметим, что значение мультипликатора Ml обычно находится приблизительно в

интервале между 2,5 и 3. Это довольно близко к нашему расчету в упрощенной мо-

дели мультипликатора, где его величина была 3,125. Иными словами, хотя наша мо-

дель и не совсем реальна, все-таки разница в расчетах не так уж велика.

Если предположить, что требуемая норма резервного покрытия для всех депозитов

была 10%, то максимальный денежный мультипликатор будет равен 10. Снятие налич-

ности со счетов и избыточные резервы являются серьезным тормозом расширения бан-

ковских депозитов. Начиная с 1983 г. мультипликатор Ml значительно увеличился;

мультипликатор М2 снижался с середины 1984 г. Как показано в главе 24, если денеж-

ГЛАВА 14 Депозитные учреждения и предложение денег

367

ные мультипликаторы далеки от стабильности, то, возможно, использование денежной

массы в качестве важной переменной, учитываемой ФРС, не так эффективно.

Также важно осознать, что эмпирические модели денежных мультипликаторов

позволяют оценивать их фактические (ех post) значения, в то время как денежно-

кредитная политика нуждается в информации об ожидаемых (ех ante) изменениях

денежных мультипликаторов. Чем разнообразнее значения денежных мультипликато-

ров,

тем сложнее проводить денежно-кредитную политику, если целью ФРС является

контроль над денежной массой. Следовательно, мультипликатор должен быть ста-

бильным и предсказуемым, чтобы модель денежного мультипликатора была действи-

тельно полезна в качестве инструмента денежно-кредитной политики.

ОБЩИЙ КРЕДИТНЫЙ 1\^УЛЬТИПЛИКАТ0Р

Кроме контроля над изменениями денежной массы ФРС обычно заинтересована в

увеличении общего объема банковского кредитования. Модель денежного мультипли-

катора включает в себя модель определения объема банковского кредитования в це-

лом, т. е. общего объема ссуд, выданных банковской системой.

I I I I I I I I I I I I I I I I I I I I I гП I I

1959 60 6162 63 64 65 6667 68 69 70 71 72 73 74 75 76 77 78 79 80

82 83 84 85 86 8788 89 90 9192 93

Год

Рис. 14-15

Расчет мультипликаторов Ml и М2. {Источник: Federal Reserve Bank of St. Louis.)

В нашей модели объем ссуд (L) представляет собой общий объем кредитования

банковской системы (то, что банки владеют ценными бумагами, мало что меняет). Если

у банков в качестве активов только ссуды и резервы, а в качестве пассивов только

трансакционные депозиты, тогда из консолидированных Т-счетов справедливо, что:

L+ TR= D.

(14-19)

Уравнение (14-19) просто показывает, что банковские активы должны быть равны

банковским пассивам. Соответственно, L

D ^ TR, так что прирост общего объема

банковского кредитования должен быть равен:

368 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

AL = AD- ATR. (14-20)

В соответствии с уравнением (14-20) прирост общего объема банковского кредитова-

ния обусловлен разницей между приростом пассивов (трансакционных депозитов) и

приростом общих банковских резервов.

Теперь можно вывести базовую модель кредитного мультипликатора. Предполо-

жим, что прирост объема банковского кредитования связан с приростом денежной

базы с помощью мультипликатора:

AL = т^х АМВ, (14-21)

где т^ и есть кредитный мультипликатор. Мы можем использовать выражение AL =

= AD — AR = AD — \(^d+ е)х AD\ д^я подстановки в левую часть уравнения (14-21).

К тому же, как известно из предыдущего изложения, АМВ = ATR + АС= (d

-h

е +

+ с) X АД так что теперь можно заменить это выражение в правой части. После этих

подстановок получим:

AD - [(d + е)х AD] = т^х {d + е + с) х AD.

Если разделить обе части уравнения на АД то имеем:

\ - {d + е) = т^х {d + е

Л-

с).

Наконец, разделим обе части последнего уравнения на величину {d

-\-

Л-

с):

'-^^^^ = т, (14-22)

d-^e

c ^

и получим выражение общего кредитного мультипликатора. Следовательно, модель де-

нежного мультипликатора, которую мы построили ранее, также включает и модель общего

кредитного мультипликатора (total credit multiplier model), которая представлена

следующим уравнением:

AL = ^^^^^-^xAMB, (14-23)

Покупка ценных бумаг ФРС на открытом рынке увеличивает денежную базу, так

что уравнение (14-23) показывает, что эта операция увеличит общий объем банков-

ского кредитования на эту сумму, умноженную на мультипликатор. В числовом при-

мере, рассмотренном выше, где d = 0,10, е = 0,05 и с = 0,25, общий кредитный

мультипликатор будет равен [1 - (0,10 + 0,05)/(0,10 + 0,05 + 0,25) = (0,85)/

(0,40),

что приблизительно составит 2,125. Это означает, что каждый доллар, вло-

женный ФРС в покупку ценных бумаг, позволит банкам увеличить объем кредитова-

ния примерно на 2,13 долл. в расчете на 1 долл. ссуд.

Как будет показано в последующих главах, ФРС не всегда придерживалась точки

зрения, что ей необходим полный контроль над денежной массой. Фактически неко-

торые экономисты утверждали, что общий объем банковского кредитования — более

подходящая переменная для контроля. Тем не менее обе переменные определяются

мультипликаторами, связанными между собой, что и показал наш анализ. Аргументы

для контроля той или другой переменной основываются на характере их воздействия

на экономику в целом. Мы обсудим некоторые из этих аргументов в части VI. Но в

ближайших главах мы сосредоточим внимание на том, почему и как создаются цент-

ральные банки, такие, как ФРС, призванные осуществлять контроль над этими пе-

ременными.

ГЛАВА 14 Депозитные учреждения и предложение денег 369

Краткое содержание

Система частичного резервного покрытия приводит к возможности многократного расши-

рения (или сужения) денежной массы в результате увеличения (уменьшения) банковских

резервов.

Когда депозитное учреждение получает прирост резервов сверх необходимого уровня, у

него появляется стимул для увеличения объема кредитования или приобретения ценных

бумаг, приносящих проценты. Оно может делать это, пока у него есть избыточные

резервы.

Новых резервов не создается, когда чек, выписанный на одно депозитное учреждение,

депонируется в другом; прирост резервов одного банка компенсируется их сокращением

у другого.

ФРС может создавать или ликвидировать резервы депозитных учреждений: вследствие

этого ФРС может менять денежную массу в обращении. Если ФРС выкупает казначей-

ские векселя у депозитного учреждения или домашнего хозяйства, которые помещают чек

ФРС в депозитное учреждение, то общие резервы банковской системы увеличатся на эту

сумму. Избыточные резервы возрастут (в меньшей степени), и депозитные учреждения

получат определенный стимул для увеличения объема кредитования путем создания транс-

акционных депозитов. В результате этого денежная масса вырастет.

Если ФРС продает казначейские векселя депозитному учреждению или домашнему

хозяйству, причем последние выписывают чек, общие резервы банковской системы со-

кратятся. Если перед этой сделкой избыточные резервы были нулевыми для банков—

участников сделки, то избыточные резервы в результате окажутся отрицательными; фак-

тические резервы будут меньше, чем обязательные. Депозитное учреждение при таком

положении вещей должно требовать возврата ссуд и не возобновлять погашенные ссуды.

Вследствие этого денежная масса уменьшится.

6. Никто не обязан иметь дело с ФРС, когда она намеревается продавать или покупать

ценные бумаги на открытом рынке; ФРС побуждает домашние хозяйства и депозитные

учреждения покупать (или продавать) ценные бумаги, предлагая на них более низкую

(или более высокую) цену. Поскольку ФРС мало волнует максимизация прибыли (и

поскольку она может покупать ценные бумаги, просто выписав чек на себя), она может

проводить такое количество операций на открытом рынке, которое считает нужным для

достижения своих целей.

Операции ФРС на открытом рынке прямо меняют общий размер резервов банковской

системы; следовательно, ФРС может изменять денежную массу. Зависимость между

приростом общих резервов и приростом банковских депозитов определяется депозитным

мультипликатором. Для определения максимального расширения объема депозитов при-

рост резервов )/множается на обратн)ао величину требуемой нормы резервного покры-

тия;

такая обратная величина называется максимальным депозитным мультипликатором.

Поскольку в США существует система частичных банковских резервов, требуемая норма

резервного покрытия будет меньше единицы и максимальный депозитный мультиплика-

тор больше единицы. Другими словами, денежная масса может изменяться кратно при-

росту общего объема резервов.

8. В мировой практике денежный мультипликатор меньше его максимальной величины,

частично из-за избыточных резервов, которые в действительности хранят депозитные

учреждения, но в основном вследствие того, что происходит утечка наличности. Такая

утечка появляется, когда экономические агенты депонируют не всю сумму чека в банк;

его часть снимается в виде наличных денег.

9. Так уж сложилось, что расширение банковских депозитов включает в себя расширение

объема банковского кредитования. Следовательно, существует зависимость как между

общим объемом кредитования и денежной базой, так и между денежной массой и де-

нежной базой, которые изменяются в кратном размере.

370 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

Словарь терминов

Денежная база (monetary base) — показатель денежной массы в обращении; равняется сум-

ме наличных денег в обращении и банковских резервов. Денежная база является основой

всех показателей денежной массы.

Денежный мультипликатор (money multiplier) — число, на которое умножается показатель

денежной массы, такой, как денежная база, чтобы получить общее количество денег в

обращении.

Депозитный мультипликатор (мультипликатор расширения депозитов) (deposit expansion

multiplier) — число, на которое умножается прирост резервов, чтобы рассчитать при-

рост общего объема депозитов в банковской системе.

Избыточные резервы (excess reserves) — резервы, которые депозитное учреждение (или

банковская система в целом) имеет сверх обязательных резервов; суммарные резервы за

вычетом обязательных.

Общий объем кредитования (total credit) — все ссуды, выданные банками.

Обязательные резервы (required reserves) — сумма резервов, которую депозитное учрежде-

ние обязано хранить в виде кассовой наличности или на резервном счете в ФРС; обя-

зательные резервы равны определенному проценту от общего объема депозитов.

Операционный отдел (Trading Desk) — название отдела в Федеральном резервном банке

Нью-Йорка, который проводит операции ФРС с ценными бумагами.

Разумные резервы (prudential reserves) — резервы, которые депозитные учреждения добро-

вольно хранят сверх обязательных, чтобы оставаться ликвидными и быть готовыми к

преодолению финансовых трудностей.

Суммарные резервы (total reserves) — сумма обязательных и избыточных резервов.

Требуемая норма резервного покрытия (required reserve ratio) — процент от общего объема

депозитов, который ФРС предписывает всем депозитным учреждениям хранить в виде

кассовой наличности или на резервном счете в ФРС.

Т-счета (T-accounts) — Т-образные бухгалтерские счета; упрощенные балансовые отчеты,

включающие только статьи активов и пассивов (или их изменения), необходимые для

анализа.

Утечка наличности (currency leakage) — снятие наличных денег небанковским сектором со

счетов депозитных учреждений.

Вопросы ДЛЯ самопроверки

Объясните своими словами, можете ли вы изменить общий объем депозитов банковской

системы, выписав чек на собственный счет для депонирования в другом банке.

Объясните своими словами, может ли ФРС изменить общий объем депозитов банков-

ской системы, выписав чек на собственный счет с последующим его депонированием на

счет продавца ценных бумаг в частном банке.

Экономистам нравится подчеркивать, что ФРС может проводить операции на открытом

рынке для контроля над денежной массой, покупая или продавая кетчуп или даже ко-

смические корабли (если бы их существовало достаточно много). Объясните, почему это

утверждение оправданно.

В экономике с фактически нерегулируемой банковской деятельностью не существует

обязательных резервов. Означает ли это, что расширение депозитов не имеет ограниче-

ний в такой системе.'^ Свой ответ обоснуйте.

Своими словами, не используя уравнений или формул, объясните, почему возрастание

утечки наличности из банковской системы сокращает эффект мультипликатора от опе-

раций ФРС на открытом рынке.

ГЛАВА 14 Депозитные учреждения и предложение денег 371

6. Объясните своими словами, не используя уравнений или формул, почему увеличение

избыточных резервов, которые банки склонны хранить (при неизменности других фак-

торов), уменьшает величину общего кредитного мультипликатора.

Задачи

14-1.

Пусть требуемая норма резервного покрытия равна 5%, избыточные резервы равны

нулю,

утечки наличности не существует и спрос на кредит постоянен. ФРС покупает

казначейские векселя у депозитного учреждения на сумму 1 млн. долл.

а) Каков будет размер максимального денежного мультипликатора.'^

б) Во сколько раз увеличится общий объем депозитов.-^

14-2.

ФРС покупает казначейские векселя на сумму 1 млн. долл. у г-на Мондроуна, который

вкладывает выручку в банк /. Используя Т-счета, покажите результат этой операции

для ФРС и банка 1.

14-3.

Продолжим пример из задачи 14-2:

а) Проанализируйте состояние банка / более подробно, используя Т-счета, если требу-

емая норма резервного покрытия по вкладам до востребования равна 5%.

б) Насколько банк 1 сможет увеличить объем кредитования.'^

14-4.

Рассмотрите балансовый отчет (в млн. долл.) отдельно взятого банка (среди многих):

Активы, долл. Пассивы, долл.

Резервы 400

Ссуды 1600

Депозиты до востребования 1000

Сберегательные депозиты 1000

Допустим, что требуемая норма резервного покрытия равна 20% по депозитам до вос-

требования и 20% по сберегательным депозитам. Если клиент снимает 100 долл. с

текущего счета, как будет реагировать на это данный банк.'^

Рассмотрите приведенный ниже консолидированный баланс коммерческих банков.

Активы, долл. Пассивы, долл.

Резервы 4000 Депозиты до востребования 10 000

Ссуды 16 000 1 Сберегательные депозиты 10 000

При той же операции (т. е. снятии 100 долл. со счета) эти средства сразу депонируются

в другом коммерческом банке. Как будет выглядеть этот консолидированный баланс.'^

14-5.

Допустим, что требуемая норма резервного покрытия равна 25% по депозитам до вос-

требования и 15% по сберегательным депозитам. Если клиент депонирует 100 долл. на

текущий счет (вклад до востребования), как будет реагировать на это отдельный банк-^

Если текущие поступления от кредитования распределяются в пропорции — 60% на

депозиты до востребования и 40% на сберегательные депозиты, определите возможные

изменения консолидированного баланса.

14-6.

Вплоть до 1990 г. ФРС установила требуемую норму резервного покрытия по срочным

депозитам юридических лиц. Если сумма таких депозитов — N и норма резервного

покрытия по вышеупомянутым депозитам, ожидаемая небанковским сектором, — л,

найдите величину денежного мультипликатора при условии, что d, е и

— положитель-

ные константы. (Подсказка: Вам необходимо попрактиковаться в выводе формулы де-

нежного мультипликатора. Подставьте вместо уравнения (14-5) выражение ATR

—

(dx

X /S.N) + (7 X АЛ9 + (е X A.N) и проделайте все математические вычисления. Чтобы

проверить их правильность, нужно удостовериться, что при ^ = О величина денежного

мультипликатора будет равна полученному ранее ответу.)

372 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

14-7.

Представьте экономику без наличных денег, где у банков нет избыточных резервов и

существует единственный вид депозитов — трансакционные депозиты. Если общая сумма

депозитов 200 млн. долл. и объем банковских резервов 50 млн. долл., какова тогда

требуемая норма резервного покрытия по данному виду депозитов.^

14-8.

Представьте экономику без наличных денег, при этом существует единственный вид

депозитов — трансакционные депозиты. Избыточные резервы банков равны 200 млн.

долл., а требуемая норма резервного покрытия — 10%. Если величина денежного муль-

типликатора 5,0, каким тогда является общий объем депозитов в банковской системе.-^

14-9.

Допустим, что в экономике единственный вид банковских пассивов — это депозиты до

востребования, при этом избыточных резервов у банков нет. Требуемая норма обяза-

тельных резервов равна 0,50 (50%). Кроме того, денежная база равна 100 млрд. долл.,

а денежная масса составляет 150 млрд. долл. Каково отношение объема наличных денег,

которые небанковский сектор склонен хранить, к объему трансакционных депозитов.'^

14-10.

Год 2310-й н. э. Поселенцы земной колонии на Титане (кр)шнейшем спутнике планеты

Сатурн) используют банковские депозиты до востребования в качестве единственного

вида денег. Банки Титана всегда хранят 10% в качестве избыточных резервов. Других

видов депозитов в банковской системе не существует. Если общие банковские резервы

Титана — 300 млн. долл. и денежная масса — 1500 млн. долл., какова требуемая норма

обязательных резервов центрального банка на Титане.'^

Рекомендуемая литература

Board of Governors of the Federal Reserve System, The Federal Reserve System: Purposes and

Functions, 7 ed. — Washington (D. C), 1984.

Crick W. F., The Genesis of Bank Deposits. — Economica, 1927.

Humphrey Thomas, The Theory of Multiple Expansion of Deposits: What It Is and Whence It

Came. — Federal Reserve Bank of Richmond Economic Review, 73 (2), March/April

1987,

pp. 3—11.

Nichols Dorothy A/., Modern Money Mechanics: A Workbook on Deposits, Currency, and Bank

Reserves. — Federal Reserve Bank of Chicago, 1961 (revised in 1968, 1971, 1975, and

1982).

Tobin James, Commercial Banks as Creators of Money, in: Carson D. (ed.), Banking and Monetary

Studies. — Homewood (111.): Irwin, 1963, pp. 408—419.

История

центрального банка США.

Федеральная

резервная система

Как экономические и политические

дискуссии конца XIX — начала XX в.

привели к образованию коалиции,

ратующей за создание центрального

банка США?

Какова история создания Федеральной

резервной системы?

Какова структура Федеральной резервной

системы в настоящее время?

Основные проблемы

Почему Первый банк Соединенных Штатов

был упразднен, став объектом

противоречий?

Какие факторы повлияли на «взлет и

падение» Второго банка Соединенных

Штатов? Повредило ли экономике США

его упразднение?

3. Какие последствия имело введение

нерегулируемой банковской деятельности

в США в середине XIX в.?

Почему гражданская война изменила

денежную и банковскую систему США?

/4^я решения различных государственных проблем (ведение войн, научных исследо-

ваний и т. д.) правительствам часто была необходима помощь финансового агента,

такого, как банк. Поэтому многие экономисты-историки считают, что необходимость

создания центрального банка (как ФРС) главным образом связана именно с прави-

тельственными нуждами.

Роль и функции федерального правительства всегда были предметом острых дис-

куссий в США. Вследствие тесного переплетения интересов федерального правитель-

ства и центрального банка существование последнего в различные периоды истории

США оказалось в центре политических дискуссий. Наши предки горячо спорили о

том, какую структуру должен иметь центральный банк; некоторые посвятили боль-

шую часть жизни борьбе за основание такого учреждения. Естественно, хотя мы

воспринимаем ФРС как само собой разумеющееся, на самом деле период ее сущест-

вования занимает лишь треть национальной истории США.

В данной главе у нас три основные задачи. Начнем мы с краткой истории централь-

ного банка США с XVIII до XX в. Затем обсудим факторы, которые способствовали

созданию Федеральной резервной системы, закончим современной структурой ФРС.

Краткая история центрального банка США

Возможно, столкнувшись с почти монопольной властью Банка Англии, основатели

США в общем были против создания центрального банка независимо от того, будет

374 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

ли он в частном или государственном управлении. К тому же существовавшие тогда

банки были против доминирования сильного национального банка, а правительства

штатов считали себя важнее федерального правительства. Поэтому деятельность бан-

ков регулировалась правительствами штатов вплоть до 1963 г., за исключением пери-

одов существования Первого и Второго банков Соединенных Штатов.

ПЕРВЫЙ БАНК СОЕДИНЕННЫХ ШТАТОВ

Как отмечалось в главе 6, Конгресс предоставил чартер Первому банку Соединенных

Штатов в 1791 г. В определенной степени этот банк выполнял многие функции цен-

трального банка. Он мог контролировать эмиссию банков штатов и выдачу ссуд. Когда

Первый банк Соединенных Штатов решал выдавать больше ссуд частным лицам и

компаниям, то резервы банков штатов увеличивались. При сокращении объема кре-

дитования резервы банков штатов также уменьшались. Первый банк мог регулировать

деятельность банков штатов и по-другому. Если Первый банк Соединенных Штатов

владел их банкнотами, то он мог хранить их (или расплачиваться ими), поэтому бан-

кам штатов не было необходимости сокращать количество золота или серебра, храни-

мых в качестве резервов. Наоборот, если Первый банк предъявлял такие банкноты к

погашению, то банки-эмитенты должны были платить золотом и серебром; их резервы

соответственно уменьшались.

Первый банк Соединенных Штатов был прибыльным, доходность для его инвес-

торов составляла примерно 8% в год. Когда подошел срок истечения чартера в 1811 г.,

Конгресс не продлил его. Было несколько причин для такого решения. Одним из

важнейших поводов для этого явился тот факт, что среди акционеров банка были

иностранцы. В то время, как и в наши дни, американцы опасались иностранного вли-

яния в экономике. Особенно эта точка зрения превалировала во время попытки Пер-

вого банка стать действительно центральным банком. Противники этого также счита-

ли,

что Первый банк Соединенных Штатов будет препятствовать росту банков шта-

тов,

постоянно предъявляя банкноты к погашению.

ВТОРОЙ БАНК СОЕДИНЕННЫХ ШТАТОВ

Во время войны 1812 г. многие лидеры пришли к мнению, что правительству США

необходим институт центрального банка в периоды кризисов. Поэтому в 1816 г. фе-

деральное правительство выдало 20-летний чартер Второму банку Соединенных

Штатов. Второй банк предоставлял услуги коммерческого характера в экономике и

одновременно вьшолнял функции центрального банка. Деятельность банков штатов он

регулировал теми же методами, что и Первый банк Соединенных Штатов.

Многие американцы с подозрением относились к могущественному Второму банку.

Более того, некоторые считали его виновным в финансовой панике 1819 г. Во время

правления влиятельного президента Второго банка Николаса Биддла (Biddle) проти-

востояние возросло. К окончанию срока назначения Н. Биддла влиятельные полити-

ческие силы делали все, чтобы чартер Второго банка не был продлен. Избрание Эндрю

Джэксона (Jackson, 1767—1845) президентом США в 1828 г. только усилило про-

блемы Второго банка. То, что «герой Нового Орлеана», родом из Теннесси, выиграл

у сторонника Второго банка Генри Клея (Clay), было только частью возникших труд-

ностей. Вдобавок к этому во время избирательной кампании большинство членов

правления и чиновников Второго банка открыто выступало против Эндрю Джэксона

и его партии. Также важен и тот факт, что Э. Джэксон — который ранее чуть не стал

банкротом из-за спекулятивных сделок с землей и поэтому не доверял банкам вооб-

ще — считал, что национальный банк будет крайне негативно влиять на американ-

ГЛАВА 15 История центрального банка США. Федеральная резервная система 375

скую экономику, будучи сильно коррумпированным. Э. Джэксон обвинил Второй банк

в монополизации американской финансовой сферы. Это послужило началом «банков-

ской войны» между Э. Джэксоном и Н. Биддлом.

В общем, самой большой политической ошибкой Н. Биддла была подача заявления

на продление чартера Второго банка за четыре года до срока его истечения. Намере-

ния Н. Биддла были такими: он хотел продлить чартер и поставить в затруднительное

положение Э. Джэксона перед выборами 1832 г. Конгресс видел, что такое продление

будет действительно полезным, и попытка Э. Джэксона воспрепятствовать принятию

этого решения по причине неконституционности провалилась, и 3 июля 1832 г. боль-

шинство в Конгрессе проголосовало за продление чартера.

Реакция Э. Джэксона была довольно характерна для него, и, возможно, это была

одна из его самых известных фраз. Он сказал вице-президенту США Мартину Ван-

Бурену (Van Buren): «Банк пытается уничтожить меня, г-н Ван-Бурен, но я сам

уничтожу его». 10 июля 1832 г. Э. Джэксон наложил вето на акт о продлении

чартера, а Конгресс не смог преодолеть вето президента. Продление чартера Второго

банка стало главным вопросом избирательной кампании 1832 г., на которой Э. Джэк-

сон победил с большим преимуществом. После выборов Э. Джэксон изъял все феде-

ральные средства из банка и поместил их в избранные банки штатов, которые назвали

«ручными» банками (pet banks).

ИНФЛЙЦ1^Я ПОСЛЕ УПРАЗДНЕНИЯ ВТОРОГО БАНКА СОЕДИНЕННЫХ ШТАТОВ

Ликвидация Второго банка Соединенных Штатов в 1836 г. внесла многие изменения в

американскую банковскую сферу. Инфляция выросла и продолжалась в 1834—1837 гг.

Экономический спад наблюдался с 1839 по 1843 г. Многие историки считают, что

инфляция и последующий экономический спад явились следствием упразднения Второ-

го банка. Они также считали, что отсутствие регулирования со стороны Второго банка

операций банков штатов привело к быстрому росту бумажных денег и появлению спе-

кулятивных банков (или банков «для диких кошек» (wildcat banks), получивших свое

название вследствие их большой отдаленности, так что, как говорили, только дикие

кошки могли их часто посещать).

Значительное увеличение денежной массы всегда приводило к обесценению денег.

Вспомните из главы 2, что цена денег есть их покупательная способность, так что

значительный прирост денежной массы обычно становится причиной инфляции. На

рис.

15-1 показано, что денежная масса действительно возросла после наложения вето

Э. Джэксоном на продление чартера Второго банка в 1832 г.

Увеличение числа спекулятивных банков не было причиной роста денежной массы

с 1832 по 1836 г. Отношение банковских резервов к объему выданных ссуд не умень-

шилось в этот период, поскольку в общем банки были достаточно осторожны. В

основном это произошло за счет увеличения количества металлических денег — зо-

лотых и в меньшей степени серебряных — в экономике США. К тому же США

были частью мировой экономики. Соединенные Штаты придерживались золотого стан-

дарта, который включал ввоз и вывоз металлических денег, и золотые и серебряные

монеты лежали в основе денежной массы в обращении. В этот период произошло

значительное увеличение импорта металлических денег из Мексики и стран Европы.

Нижняя кривая на рис. 15-1 показывает, что количество металлических денег,

ввозимых в США, сильно возросло в период с 1832 по 1837 г. Было три основные

причины этого:

Увеличение экспорта американского хлопка в Англию.

Иностранные инвестиции в развивающуюся транспортную систему США.