Миллер Р.Л., Ван-Хуз Д.Д. Современные деньги и банковское дело

Подождите немного. Документ загружается.

356

ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

Рис. 14-7

Банк 1

Активы,

долл.

Суммарные резервы 110 000

Обязательные резервы

(110 000)

Избыточные резервы

(0)

Ссуды 990 000

Итого 1 100 000

Пассивы, долл.

Трансакционные

депозиты 1 100 000

Итого 1 100 000

Те,

кто получил ссуду из этих 90 000 долл., потратят эти средства, которые затем

попадут в другие банки.

]Х^\я

упрощения данного примера допустим, что 90 000 долл.

избьпючных резервов выдали в качестве ссуды некой фирме для покупки лицензии компании

Burger King. После продажи лицензии Burger King депонирует 90 000 долл. в банке 2.

Для упрощения анализа не обращайте внимания на предыдущие активы и пассивы банка

2 и рассматривайте только изменения в Т-счетах, происшедшие в результате открьггия

нового депозита (рис. 14-8). Знак «плюс» означает, что поступления увеличились, знак

«минус» — наоборот. Для банка 2 депозит в 90 000 долл., после того как чек был

депонирован ФРС, становится увеличением резервов (активов), так же как и приростом

трансакционных депозитов (пассивов). Поскольку требуемая норма резервного покрьггия

равна 10%, или 9000 долл., банк 2 будет обладать избьп-очными резервами в 81 000 долл.

Но конечно, избьп-очные резервы не приносят доходов, поэтому банк 2 снизит их до нуля,

выдав ссуды на сумму в 81 000 долл. (которые будут приносить доход) (рис. 14-9).

Рис. 14-8

Банк 2

Активы,

долл.

Пассивы, долл.

Суммарные резервы

Обязательные резервы

(9000)

Избыточные резервы

(81 000)

Итого

90 000

+90J)00

Новые трансакционные

депозиты

Итого

90 000

+90 000

Рис. 14-9

Банк 2

Активы,

долл.

Пассивы, долл.

Суммарные резервы

Обязательные резервы

(9000)

Избыточные резервы

(0)

Ссуды

Итого

+9000

+81 000

+90 000

Трансакционные

депозиты

Итого

+90 000

ГЛАВА 14

Депозитные учреждения и предложение денег 357

Напомним, что в данном примере первоначальный вклад в 100 000 долл. был

чеком, который выписал банк на ФРС. Эта сумма немедленно увеличила денежную

массу на 100 000 долл. Процесс создания денег (в дополнение к первоначальной

сумме) происходит вследствие дробления резервов в банковской системе, плюс склон-

ность депозитных учреждений поддерживать избыточные резервы на нулевом уровне

(при условии достаточного спроса на ссуды).

Продолжение процесса расширения депозитов Допустим, еще одна фирма полу-

чила ссуду в банке 2 в размере 81 000 долл., так как она хочет приобрести нефте-

добывающую компанию. У последней есть счет в банке 3. Рассмотрим упрощенный

баланс (Т-счет) банка 3 (рис. 14-10), где показаны только увеличение активов и

пассивов. Когда фирма, взявшая ссуду в банке 2, выплачивает 81 000 долл. директору

нефтедобывающей компании, последний депонирует чек в банке 3. Суммарные резер-

вы банка 3 увеличиваются на эту сумму, когда чек депонируется ФРС.

Рис. 14-10

Банк 3

Активы,

долл.

Суммарные резервы +81 000

Обязательные резервы

(8100)

Избыточные резервы

(72 900)

Итого +81 000

Пассивы,

долл.

Новые трансакционные

депозиты +81 000

Итого +81 000

Поскольку требуемая норма резервного покрытия равна 10%, то обязательные резер-

вы увеличатся на 8100 долл., а избьггочные резервы возрастут до 72 900 долл. Банк 3

будет склонен выдать новую ссуду из не приносящих доход избыточных резервов.

Когда это произойдет, общий объем кредитования увеличится на 72 900 долл. Сум-

марные резервы уменьшатся до 8100 долл., избыточные резервы станут равны нулю,

когда директор нефтедобывающей компании выпишет чек и депонирует его в банке.

Общий объем депозитов — и денежной массы — вследствие этого увеличится еще

на 72 900 долл. (рис. 14-11).

Рис. 14-11

Банк 3

Активы,

долл.

Пассивы,

долл.

Суммарные резервы 8100

Обязательные резервы

(8100)

Избыточные резервы

(0)

Ссуды 72 900

Трансакционные

депозиты

81 000

Итого 81 000 Итого 81 000

Процесс продолжается с банками 4, 5, 6 и т. д. Этот процесс пойдет дальше.

Каждый банк будет получать все меньший и меньший прирост депозитов, ведь 10%

всегда должно находиться в резервах; следовательно, каждое последующее депозит-

358 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

ное учреждение будет выдавать соответственно меньший объем ссуд. В табл. 14-1

показаны новые депозиты, возможные ссуды и инвестиции, обязательные резервы

всех других депозитных учреждений.

Как изменились общий объем депозитов и денежная масса.^ В данном )шрощенном

примере общий объем трансакционных депозитов и, следовательно, объем денежной

массы, первоначально увеличился на 100 000 долл., которые ФРС заплатила продавцу

облигации. Трансакционные депозиты возросли далее на размер вклада в банк 2 в сумме

90 000 долл. А затем они еще увеличились на 81 000 долл., вложенных в банк 3,

Постепенно объем депозитов и денежная масса возрастут до 1 млн. долл. Это показано

в табл. 14-1 и графически представлено на рис. 14-12.

ТАБЛИЦА 14^1

Максимальный потенциальный эффект на прирост денежной массы от увеличения

резервов на 100 000 дол

л* ^ру\

требуемой норме резервного покрытия в tO%

Банк

Все другие банки

Итого

Новые депозиты

100 000

000

900

610

049

144

830

430

467

1^000 000

Возможные ссуды

и инвестиции

(избыточные резервы)

000

900

610

049

144

830

047

387

420

900

000

Обязательные

резервы

000

300

100

290

561

905

314

783

047

100000

CyiVIIVIAPHblE РЕЗЕРВЫ ДОЛЖНЫ У8ЕЛ1/1ЧИТЬ0Я, ЧТОБЫ ПРОИЗОШЛО

МУЛЬТИПЛИКАТИВНОЕ РАСШИРЕНИЕ ДЕПОЗИТОВ

Даже при системе частичного резервного покрытия и нулевых избыточных резервах

объем депозитов и денежная масса не могут увеличиваться без прироста суммарных

резервов. Первоначальный депозит в банк \ в предыдущем примере был в форме

чека, выписанного на федеральный резервный банк соответствующего округа. По-

этому он представлял собой новые резервы для банковской системы. Если бы чек

был выписан, к примеру, на банк 5, то общий объем трансакционных депозитов не

претерпел бы изменений и денежная масса осталась Ьы прежней. Еще раз повторим:

чеки, выписанные на другие банки, представляют собой взаимоисключающие акти-

вы и пассивы. Только при создании избыточных резервов в банковской системе

денежная масса может увеличиться.

Выводы будут те же, как и в том случае, если бы в нашем примере депозит-

ные учреждения использовали свои избыточные резервы вместо выдачи ссуд для

покупки ценных бумаг, приносящих проценты. Владельцы этих ценных бумаг полу-

чат чеки от депозитного учреждения, осуществляющего покупку; продавцы ценных

бумаг затем депонируют эти чеки в свои депозитные учреждения. Процесс расшире-

ния депозитов будет продолжаться точно так же.

ГЛАВА 14 Депозитные учреждения и предложение денег 359

1 2 3

Первоначальные

депозиты

4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Стадии расширения

1 000 000

900 000

800 000

700 000

600 000

500 000

400 000

300 000

200 000

100 000

Всего

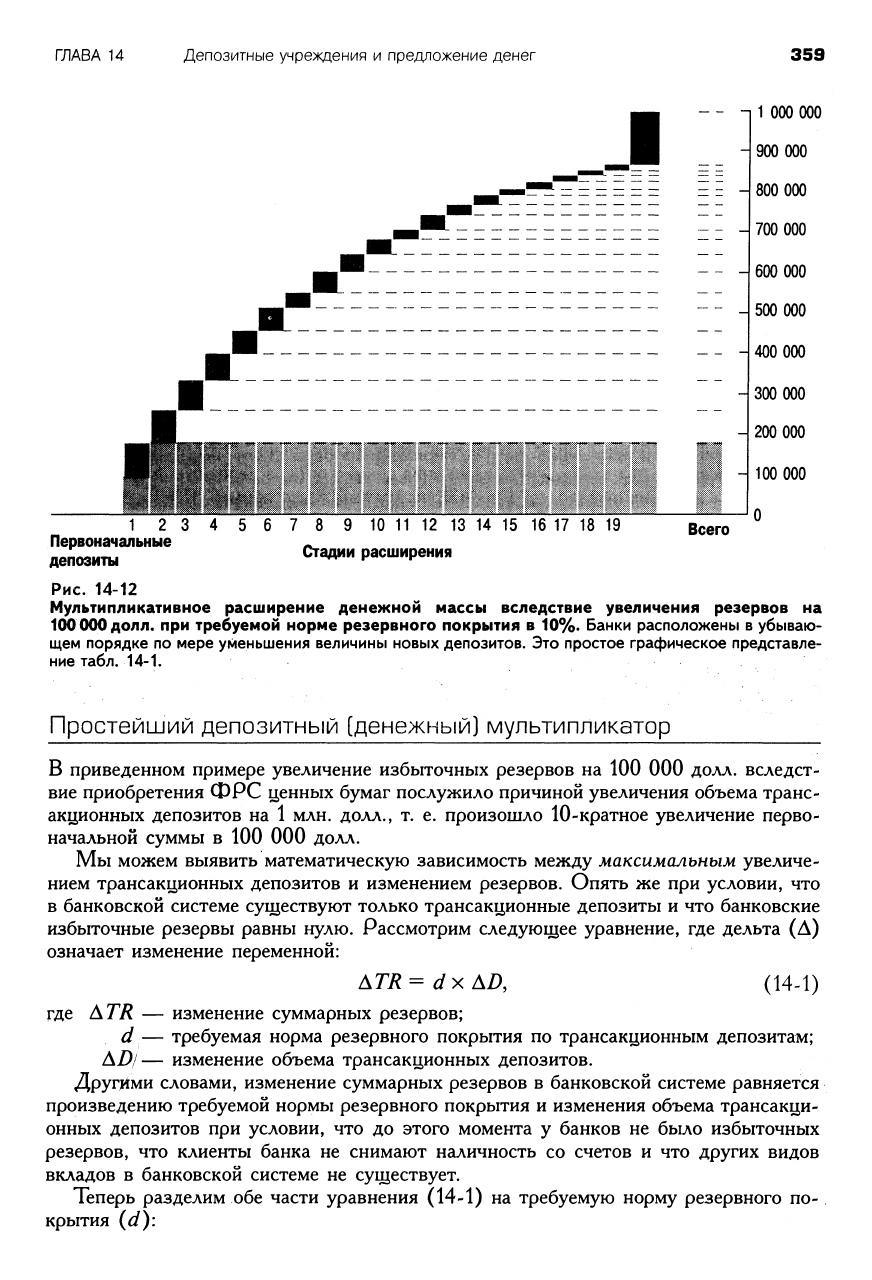
Рис. 14-12

Мультипликативное расширение денежной массы вследствие увеличения резервов на

100000 долл. при требуемой норме резервного покрытия в 10%. Банки расположены в убываю-

щем порядке по мере уменьшения величины новых депозитов. Это простое графическое представле-

ние табл. 14-1.

Простейший депозитный [денежный] мультипликатор

В приведенном примере увеличение избыточных резервов на 100 000 долл. вследст-

вие приобретения ФРС ценных бумаг послужило причиной увеличения объема транс-

акционных депозитов на 1 млн. долл., т. е. произошло 10-кратное увеличение перво-

начальной суммы в 100 000 долл.

Мы можем выявить математическую зависимость между максимальным увеличе-

нием трансакционных депозитов и изменением резервов. Опять же при условии, что

в банковской системе существуют только трансакционные депозиты и что банковские

избыточные резервы равны нулю. Рассмотрим следующее уравнение, где дельта (А)

означает изменение переменной:

ATR =

dxAD,

(14-1)

где

А 77?

— изменение суммарных резервов;

d— требуемая норма резервного покрытия по трансакционным депозитам;

А/)/—

изменение объема трансакционных депозитов.

Друг^йми словами, изменение суммарных резервов в банковской системе равняется

произведению требуемой нормы резервного покрытия и изменения объема трансакци-

онных депозитов при условии, что до этого момента у банков не было избыточных

резервов, что клиенты банка не снимают наличность со счетов и что других видов

вкладов в банковской системе не существует.

Теперь разделим обе части уравнения (14-1) на требуемую норму резервного по-

крытия (d):

360 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

ATR^dxAD

d d ' ^ ^

Это уравнение можно упростить, принимая, что ATR/d = (\/d) X ATR в левой части

уравнения и что d/d = 1 в правой его части, так что

-xATR = AD, (14-3)

^^авнение (14-3) показывает, что изменение суммарных резервов (в соответствии с

нашими допущениями) увеличит трансакционные депозиты в {\/d) X ATR раз. Выра-

жение \fd — это депозитный мультипликатор (мультипликатор расширения депо-

зитов) {deposit expansion multiplier). При условии, что трансакционные депозиты —

единственная форма денег, депозитный мультипликатор также можно назвать денеж-

ным мультипликатором {money multiplier), т. е. это число, на которое нужно умножить

резервы, чтобы получить общее количество денег в обращении. Этот мультипликатор

является также числом для подсчета изменения общего объема депозитов в банковской

системе при изменении резервов. Рассмотрим взятый ранее пример. ФРС увеличила

резервы на 100 000 долл., требуемая норма резервного покрьггия была равна 10%

(0,10).

Подставив эти цифры в уравнение (14-3), получим следующее:

— X100000 = 10x100000 = 1000000 долл. (14-4)

0,10 ^ ^

В данном примере денежный мультипликатор был равен 10 :

1/0,10

= 10.

Депозитный мультипликатор, приведенный в уравнении (14-3), можно использо-

вать и для оценки уменьшения депозитов. Если ФРС продает казначейские векселя

за 100 000 долл., то резервы банковской системы уменьшатся на 100 000 долл. При

условии, что норма резервного покрытия составляет 10%, объем трансакционных

депозитов, а следовательно, и денежная масса уменьшатся на 1 млн. долл.

По этой формуле рассчитывается максимальная величина, на которую могут изме-

ниться объем депозитов и денежная масса вследствие изменения резервов, или мак-

симальные депозитный и денежный мультипликаторы. Эта формула описывает

весьма упрощенную ситуацию, в которой существуют только трансакционные депози-

ты с определенной требуемой нормой резервного покрытия, клиенты банка не снима-

ют наличность со счетов, а банковские избыточные резервы всегда равны нулю. В

действительности требуемая норма резервного покрытия для различных трансакцион-

ных депозитов далеко не одна и та же. Например, в апреле 1992 г. требуемая норма

резервного покрытия для первых 42,2 млн. долл. на текущих счетах для всех банков

была 3%; 10-процентная ставка применялась ко всем депозитам сверх этой суммы.

К тому же банки могут хранить избыточные резервы, даже если они не приносят

дохода в виде процентов. Более того, когда небанковский сектор захочет снять опреде-

ленную сумму наличности с банковских счетов, величина денежного мультипликатора

изменится. Теперь мы приступим к рассмотрению общего денежного и кредитного муль-

типликаторов, которые учитывают вышеперечисленные факторы.

Общий денежный и кредитный мультипликаторы

В действительности некоторые из допущений, которые мы использовали при выведении

максимального денежного мультипликатора, редко имеют место на практике. Банки все

ГЛАВА 14

Депозитные учреждения и предложение денег

361

же хранят (хоть и в небольшом размере) избыточные резервы. Небанковский сектор

снимает наличные деньги со счетов. (К тому же ФРС может вводить обязательные

резервы для срочных вкладов; однако в настоящее время она этого не делает, поэтому

можно не обращать внимания на это дополнительное теоретическое усложнение.) Сле-

дует обязательно рассмотреть все эти факторы для понимания того, каким образом

определяется денежный мультипликатор на практике.

Более того, денежная масса — это не единственная переменная, на которую может

влиять ФРС. Ее также интересует объем предоставляемых банками ссуд, т. е. общий

объем кредитования (total credit). И как мы увидим, анализировать эту проблему

можно, используя принцип мультипликатора.

УТЕЧКА НАЛИЧНОСТИ И ПОЛОЖИТЕЛЬНЫЕ ИЗБЫТОЧНЫЕ РЕЗЕРВЬ!

Для начала снимем два из наших допущений. Во-первых, предположим, что на самом

деле компании и частные лица снимают наличность с банковских счетов. На практике

денежная масса, конечно, состоит из предложения денег со стороны банков (bank-

supplied money) — трансакционных депозитов и из предложения денег со стороны

государства (government-supplied money) — наличных денег. Как мы покажем ниже,

совокупное предложение денег со стороны государства состоит из банковских резер-

вов и наличных денег в обращении. Поэтому наличные деньги — важная часть на-

шего анализа, и необходимо их обязательно учитывать. Во-вторых, допустим, что

банки склонны иметь положительные избыточные резервы. На практике это так и

есть,

поэтому нужно сделать необходимые выводы из этого факта.

Механизм Т-счетов Возьмем предыдущий пример покупки ФРС облигаций на

сумму 100 000 долл. Банк / получает первоначальный вклад от продавца этой обли-

гации (рис. 14-13). Эта операция в точности повторяет начало первого примера, по-

этому на рис. 14-13 показаны те же уровни суммарных резервов, ссуд и депозитов,

как и на рис. 14-6.

Рис. 14-13

Банк 1

Активы,

долл. Пассивы, долл.

Суммарные резервы

Обязательные резервы

(110 000)

Избыточные резервы

(90 000)

Ссуды

Итого

200 000

900 000

1 100 000

Трансакционные

депозиты

Итого

1 100 000

Теперь предположим, что все представители небанковского сектора, включая про-

давца, захотят располагать суммой наличности, которая будет постоянной частью их

трансакционных депозитов. Это упрощенное предположение, но оно вполне логично,

если обычно совершаются сделки с наличностью, объем которых составляет опреде-

ленную долю от сделок, оплачиваемых чеками. Более того, предположим, что доля

этой наличности будет составлять V4 часть, или 25% от трансакционных депозитов.

При этом продавец облигации снимает со счета 20 000 долл. сразу после внесения

первоначального депозита в 100 000 долл. в банк 7. (ФРС переводит деньги за

покупку ценных бумаг путем их прямого зачисления в депозит (direct deposits), по-

362 ЧАСТЬ IV Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

этому снять деньги со счета можно довольно оперативно; это будет обсуждаться далее

в главе 16.)

Когда продавец снял деньги со счета, остаток вклада уменьшится до 80 000 долл.

Следовательно, общий объем трансакционных депозитов банка 1 после снятия денег со

счета будет равным 1 080 000 долл., как показано в правой части Т-счета (рис. 14-14).

Другими словами, чистый прирост депозитов в банке / составит 80 000 долл. и отноше-

ние наличных денег продавца к трансакционным депозитам будет равно 20 000 долл./

80 000 долл. = 0,25. Продавец Достигнет ожидаемого соотношения наличных денег в

его распоряжении и депозитов. Когда продавец снял деньги с банковского счета, общие

резервы банка 1 снизились на величину этого снятия, т. е. на 20 000 долл., как показано

в левой части Т-счета (рис. 14-14). Объем его трансакционных депозитов будет равен

теперь

080 000 долл., а обязательные резервы — 108 000 долл. (общая сумма трансак-

ционных депозитов, умноженная на требуемую норму резервного покрытия, или

1 080 000 долл. X 0,10), а избыточные резервы — 72 000 долл. (суммарные резер-

вы минус обязательные резервы, или 200 000 долл. — 108 000 долл.).

Рис. 14-14

Банк 1

Активы,

долл

Суммарные резервы

Снятие наличности

Чистые суммарные

резервы

Обязательные

резервы

(108 000)

Избыточные

резервы

(72 000)

Ссуды

Итого

200 000

-20 000

180 000

900 000

1 080 000

Пассивы, долл.

Трансакционные

депозиты 1 100 000

Снятие наличности —20 000

Чистые трансакционные

депозиты 1 080 000

Итого 1 080 000

Экономисты называют такое снятие наличности утечкой наличности {currency

leakage).

Если представить процесс расширения депозитов как поток денежных средств,

проходящих через депозитные учреждения, то снятие наличности продавцом облига-

ции представляет собой утечку из этого потока. В предыдущем примере мы не при-

нимали в расчет возможность такой утечки, которая должна была уменьшить депозит-

ный мультипликатор.

Другой фактор, который мы не учитывали, — это возможность того, что депозит-

ные з^реждения захотят иметь избыточные резервы (иногда их называют разумными

резервами — prudential reserves). Это происходит, когда ожидается значительное

повышение процентных ставок (что снизит стоимость покупаемых облигаций), или

если экономика находится в преддверии спада (что увеличит риск невозврата ссуд и

процентов по ним и заставит вкладчиков снимать деньги со счетов).

Для упрощения предположим, что банки хранят избыточные резервы в постоянной

пропорции к сумме новых трансакционных депозитов. В частности, пусть эта пропорция

равна 5% от всех дополнительных трансакционных депозитов. Это означает, что если

текущие избьггочные резервы равны 72 000 долл., то банк 1 будет держать только

4 000 долл. (трансакционные депозиты, умноженные на ожидаемый уровень избьггоч-

ных резервов, или 80 000 долл. X 0,05). Таким образом, остается 68 000 долл. неже-

лательных избыточных резервов, которые банк 1 хотел бы выдать в виде ссуд.

ГЛАВА 14 Депозитные учреждения и предложение денег 363

Это — сумма первоначального вклада, который получил бы банк 2, если бы не

было утечки наличности. Вкладчик банка — фирма Burger King хочет располагать V4

частью внесенного депозита. Это значит, что банк 2 в действительности получит

чистый депозит в размере 54 400 долл., а утечка наличности составит 13 600 долл.

Так что отношение наличности к депозитам фирмы Burger King будет 13 600 долл./

54 400 долл. = 0,25.

Таким образом, на первом этапе после покупки ФРС ценных бумаг на сумму

100 000 долл. первоначальный прирост депозитов банковской системы обеспечен за

счет увеличения депозитов банка 1 на 80 000 долл. (против 100 000 долл. в первом

примере, в котором не учитывалась возможность утечки наличности). На втором этапе

чистый прирост депозитов в банке 2 равен 54 400 долл. (против 90 000 долл. в

первом примере).

Ясно,

что расширение депозитов в нашем примере значительно меньше при утечке

наличности и избыточных резервах банков. И это вполне логично.

Расчет нового депозитного мультипликатора Поскольку расширение депозитов в

нашем примере будет меньше, то и депозитный мультипликатор будет соответственно

ниже. Отметим, что суммарные резервы банковской системы изменятся в размере:

АТТг = (dx AD) + (е X AD) = (d-\-е) х ДД (14-5)

где е — отношение избыточных резервов к трансакционным депозитам, которое в

нашем примере было равно 0,05 (5%). Первое выражение в правой части уравнения

(14-5) — изменение обязательных резервов вследствие изменения общего объема

трансакционных депозитов, второе выражение — изменение избыточных резервов;

сумма этих двух выражений и есть изменение суммарных резервов в левой части

уравнения.

В нашем примере утечка наличности была равна

АС= сх АД (14-6)

где С — банковские резервы и с — величина отношения наличных денег к объему

трансакционных депозитов, ожидаемая небанковским сектором. Наличные деньги в

США состоят из банкнот ФРС, и, таким образом, сумма в левой части уравнения

(14-6) представляет собой именно банкноты ФРС, предложение которых обеспечи-

вается путем распределения резервов банковской системы для удовлетворения спроса

на деньги небанковского сектора.

При этом оба уравнения (14-5) и (14-6) показывают, насколько вырастает пред-

ложение денег со стороны ФРС вследствие ее операций на открытом рынке. Общий

прирост предложения денег со стороны государства будет равен сумме уравнений (14-5)

и (14-6), т. е.

ATR + АС =[(d + е) + AD] + (с х AD) = (d + е + с) х AD. (14-7)

Левая часть уравнения (14-7) — общее изменение предложения денег со стороны

государства. Правая часть уравнения показывает, что такое изменение зависит от

изменения объема депозитов в банковской системе, которое в свою очередь зависит от

требуемой нормы резервного покрытия, уровня избыточных резервов, ожидаемого

банками, и отношения наличных денег к объему трансакционных депозитов, ожидае-

мого небанковским сектором.

При современной системе неразменных денег, когда последние не обеспечены зо-

лотом, предложение денег со стороны государства составляет денежную базу (monetary

3.64 ЧАСТЬ

Операции центрального банка: денежно-кредитная политика

и Федеральная резервная система

base).

Экономисты иногда называют денежную базу деньгами повышенной мощно-

сти (high-powered money),

так как они

лежат

основе денежной системы.

Как от-

мечалось

главе

2, при

золотом стандарте денежная база состояла

из

металлических

монет.

При

современном бумажно-денежном стандарте

она

равна:

МВ

= TR+ Q

(14-8)

где

MB —

денежная база. Следовательно, изменение денежной базы составляет:

АМВ =A77?

+АС.

(14-9)

Таким образом, денежная база изменяется

результате изменений суммарных резер-

вов

количества наличных денег

небанковского сектора. Уравнение (14-9)

— это

левая часть уравнения (14-7). Поэтому

мы

можем переписать уравнение (14-7) сле-

дующим образом:

АМВ

= {d+e +

c)xAD, (14-10)

Если

мы

разделим

обе

части уравнения (14-10)

на

величину

{d + е + с), то

полу-

чим:

xAMB

= AD.

(14-11)

Уравнение (14-11) показывает,

что

расширение депозитов

банковской системе

(правая часть уравнения) равно изменению денежной базы, умноженному

на

опреде-

ленный коэффициент (левая часть уравнения). Депозитный мультипликатор составит

теперь

l/(d + е + с).

Используя данные

из

нашего примера

(d = 0,10, е = 0,05,

0,25), найдем,

что

мультипликатор равен

1/(0,10 + 0,05 +

0,25)=1/0,40=2,5.

Напомним,

что

денежный мультипликатор

предыдущем примере

был

равен просто

\/d

= 1/0,10 =10,

поскольку

мы не

брали

расчет утечку наличности

возможность

избыточных резервов,

т.

е. е и с

равны нулю.

На

практике

же

часто

это не так

(хотя

величина

обычно меньше

0,05, как в

нашем примере). Поэтому

на

практике депозит-

ный мультипликатор

общем намного меньше максимального мультипликатора {\/d).

ОЕЩШШ

ДЕНЕЖНЫЙ 1У!У.ПЫ^ПЛИКДТ0Р

В первом примере,

где не

было утечки наличности

избыточных резервов, депозит-

ный мультипликатор показывал, насколько увеличится денежная масса вследствие

по-

купки

ФРС

ценных бумаг

на

сумму

100 000

долл. Теперь следует напомнить,

что

денежная масса

соответствии

определением

ФРС

денежного агрегата

Ml (см.

гла-

ву

равна:

Л/

= С+Д

(14-12)

где

М —

денежная масса.

Это

означает,

что

изменение денежной массы составит

= АС + АД

(14-13)

т.

е.

денежная масса меняется

ответ

на

изменения объема наличности

небанковско-

го сектора

трансакционных депозитов.

Расчет денежного мультипликатора Теперь можно рассчитать общий денежный

мультипликатор, более приемлемый

на

практике

для

банковской системы. Обозначим

его

т.

Этот мультипликатор показывает, насколько изменилась денежная масса

ответ

на

изменение денежной базы вследствие,

примеру, операций

ФРС по

продаже

ГЛАВА 14 Депозитные учреждения и предложение денег

365

или покупке ценных бумаг на открытом рынке. Следовательно, денежный мультипли-

катор входит

следующее уравнение:

АМ= тхАМВ,

(14Л4)

т. е. изменение денежной массы равно произведению денежного мультипликатора на

изменение денежной базы.

Из уравнения (14-13) следует, что левую часть уравнения (14-14) можно прирав-

нять

АС.

тому же из уравнения (14-10) вытекает, что правую часть урав-

нения (14-14) можно переписать

виде т X (А77? + АС), так что уравнение (14-14)

будет представлено следующим образом:

AD +

АС= тх

(А77?

АС). (14Л5)

Можно сделать еще несколько замен, используя уравнения (14-6)

(14-7),

вместо АС подставить с

AD в левую часть уравнения (14-15) и заменить А77? + АС

на

-Ь

-\-

с)

правой его части. Мы получим следующее:

А7)

(с X AT))

m X (^f +

е +

с) X AD. (14Л6)

Теперь разделим обе части уравнения (14-16) на 7) и будем иметь:

1 4-

с =

m X (^ +

е +

с).

Разделив

обе

части уравнения

на

этот раз

на {d

•¥

+ с),

получим:

d + e +

= т.

(14-17)

Таким образом, общий денежный мультипликатор равен (1

+ c)/(d

е + с).

В нашем примере

с =

0,25,

= 0,10

и е

= 0,05. Следовательно, общий денежный

мультипликатор для гипотетической экономики равен

(1 +

0,25)/(0,10

0,05

+ 0,25)

1,25/0,40

=3,125.

Модель денежного мультипликатора Теперь мы установили, что на практике изме-

нение денежной массы будет равно:

АМ=

^"^^

хАМВ.

Поскольку мы учли все важные факторы, действительно влияющие на денежную

массу, теперь из этого уравнения символ А можно опустить. При этом мы получим:

М = X MB. (14-18)

d+e+c ^ ^

Уравнение (14-18) показывает, что фактическая денежная масса

(М)

равна произве-

дению денежного мультипликатора на денежную базу (MB), которая

свою очередь

равна суммарным резервам банков (77?) плюс наличность (С), или общему предло-

жению денег со стороны государства.

Экономисты называют уравнение (14-18) моделью денежного мультипликатора

(money multiplier model) определения денежной массы

экономике. Если бы мы

знали точные значения

с, d и е в

будущем,

то в

принципе могли бы использовать