Миллер Р.Л., Ван-Хуз Д.Д. Современные деньги и банковское дело

Подождите немного. Документ загружается.

156 ЧАСТЬ II Финансовые инструменты, рынки и институты

текущая продажная цена облигации.»^ В соответствии с нашим уравнением (учитывая,

что в конце третьего года владелец облигации получает купонный доход 50 долл. и ему

выплачивается номинальная стоимость облигации, и игнорируя дополнительные слож-

ности, связанные с обычной практикой выплаты купонного дохода один раз в полгода)

имеем:

Р = 50долл./(1Д)+50долл./(1,1)^ + 1050долл./(1,1)^ =

= 45,45 долл. + 41,32 долл. + 788,88 долл. = 875,65 долл. (7-2)

Поскольку дисконтированная стоимость облигации равна 875,65 долл., конкурент-

ный рьшок оценит эту облигацию в точности по ее экономической стоимости.

Полезно рассмотреть, что означает величина 875,65 долл. в этом контексте. Если

кто-то намерен в настоящий момент осуществить инвестиции в облигации, которые

будут приносить ежегодный купонный доход 10%, он может получить 50 долл. в

первый год, 50 долл. — во второй и 1050 долл. — в третий. Поэтому облигация,

которая приносит доход 50 долл. в год в течение трех лет и по которой в конце

третьего года выплачивается 1000 долл. номинала, имеет текущую стоимость

875,65 долл. при рыночной процентной ставке 10%.

Доходность при погашении и дисконтирование Мы теперь можем вернуться к

первоначальному вопросу. Какова доходность при погашении 3-летней облигации

номиналом 1000 долл. с ежегодным купонным доходом 50 долл. (т. е. 5%), если ее

текущая цена равна 875,65 долл..'^ Воспользуемся для расчета доходности при пога-

шении этой облигации уравнением (7-1). В него следует подставить Р = 875,65 долл.,

R = R^ = 50 долл., R^ = 1050 долл., а г является неизвестной искомой величиной.

Итак,

875,65 дол\. =

50 доАл./(1

+ г) +50 дол\.

/(Ц-г)^

+ 1050

долл./(1

+ г) .

Решая уравнение, найдем

г = г = 0,10 = 10%,

где г — доходность при погашении. Поскольку расчет г^ довольно сложен, лучше

вычислять доходность при погашении с помощью специальных таблиц или програм-

мируемого калькулятора. В табл. 7-1, являющейся частью таблицы данных по реаль-

ным облигациям, приведены сведения о доходности при погашении облигаций с раз-

ными сроками погашения, номиналом 1000 долл. и с номинальной доходностью 6%.

Рынок долгосрочных облигаций Облигации — кредитные инструменты, которые

торгуются на рьшках облигаций. Здесь как обычно цену определяет соотношение спроса

и предложения; цена облигации определяется точкой пересечения кривых предложения

и спроса. Рассмотрим рис. 7-8, на котором показаны спрос и предложение 3-летних

облигаций с номинальной доходностью 5%.

Спрос на облигации отражает намерения кредиторов (покупателями облигаций яв-

ляются кредиторы), и они приобретут больше облигаций по низкой цене, чем по вы-

сокой. Это определяется тем, что облигации приносят фиксированный и определенный

поток доходов R, Чем ниже цена облигации, тем выше доходность при погашении; чем

выше доходность при погашении, тем больше людей готовы предоставить ссуду.

Отметим, что кривая спроса на облигации аналогична кривой предложения кредита,

приведенной на рис. 7-1 и 7-3.

Кривая предложения облигаций отражает намерения заемщиков; продавцами обли-

гаций являются заемщики, которые предлагают больше облигаций при высокой цене,

чем при низкой. Как уже отмечалось, поскольку поток доходов R по облигации посто-

ГЛАВА 7

Процентные ставки

157

янен, более высокие цены на облигации означают более низкую доходность при пога-

шении. Продавцы облигаций хотят поставлять больше облигаций (т. е. занимать боль-

ше) при низкой доходности, чем при высокой.

Цена

облигации, г

$922,69

$875,65

$831,87

Спрос и предложение облигаций

в единицу времени

Рис. 7-8

Спрос и предложение 3-летних облигаций с номинальной доходностью 5%. Этот рисунок показы-

вает, что равновесная цена установится на уровне 875,65 долл., если рыночная процентная ставка равна

10%.

При более высокой цене, скажем 922,69 долл., возникает избыточное предложение облигаций.

Такая цена соответствует доходности при погашении 8%, поэтому такая ситуация соответствует ситуа-

ции с недостаточным предложением кредита (рис. 7-3). Избыточное предложение облигаций означает,

что существует нехватка средств для заемщиков. При более низкой цене, скажем 831,87 долл., возни-

кает недостаточное предложение облигаций. При такой цене на облигации доходность при погашении

равна 12%, и существует избыточное предложение кредита (рис. 7-3). Недостаточное предложение

облигаций приводит к тому, что кредиторы не находят нужного числа заемщиков при существующей

цене на облигации.

ТАБЛИЦА 7-1

Часть облигационной таблицы

pjrm

облигаций с 6 %-й номинальной доходностью

Предположим, что облигация номиналом 1000

долл.,

с номинальной доходностью 6%

сроком погашения в 7Уг ^^т

может быть приобретена приблизительно за 900 долл. Владелец получит 1000 долл. в конце периода. Для вычис-

ления доходности при погашении, или суммарной фактической доходности, найдите число, ближайшее к 90,00 в

колонке срока погашения в 7 Vj

-"^т.

Это число 89,92, или 899,20

долл.,

которое является ближайшим числом к 900

долл.

В крайней левой колонке найдите соответствующую доходность при погашении 7,8% для 6-процентной

купонной облигации или номинальную доходность облигации номиналом 1000 долл.

Доходность при погашении, %

(годовая доходность 6%)

Годы до погашения

95,17

94,24

93,31

92,40

91,50

90,61

6V,

94,85

93,86

92,88

91,91

90,96

90,01

94,54

93,49

92,46

91,44

90,43

89,44

7V.

94,24

93,14

92,05

90,98

89,92

88,88

93,95

92,80

91,66

90,54

89,44

88,35

7,00

7,20

7,40

7,60

7,80

8,00

Изучите рис. 7-8 и сравните его с рис. 7-3. Цена облигации 922,69 долл. соответ-

ствует доходности при погашении 8% (для 3-летней облигации с номинальной доход-

ностью 5%). Такая ситуация создает избьггочное предложение облигаций (рис. 7-8) и

недостаточное предложение кредита (рис. 7-3). Избыточное предложение облигаций

158 ЧАСТЬ II Финансовые инструменты, рынки и институты

приводит к тому, что продавцы облигаций (заемщики) не находят достаточного числа

покупателей (кредиторов). Следовательно, существует нехватка кредита, и процентная

ставка вырастет — цены на облигации упадут.

При цене 831,87 долл., которая соответствует доходности при погашении 12%,

возникает недостаточное предложение облигаций (рис. 7-8) и избьггочное предложе-

ние кредита (рис. 7-3). Недостаточное предложение облигаций приводит к тому, что

покупатели облигаций (кредиторы) не могут найти нужного числа продавцов (заем-

щиков). Если кредиторы не могут найти достаточного числа заемщиков при сущест-

вующей процентной ставке, возникает избыток кредита, и процентная ставка упа-

дет -— цена облигаций вырастет.

ДОХОД ПО БЕССР0ЧНЫ1У1 0БЛИГАЦ1^ЯГУ! |К0НС0ЛЯ1У1}

Рассмотрим экономику, в которой существует только одна процентная ставка, изме-

няющаяся во времени в зависимости от соотношения спроса и предложения кредита

(ссудного капитала). Предположим также, что существует всего одна облигация но-

миналом 1000 долл., каждая новая эмиссия которой осуществляется правительством

ежегодно 1 января. Купонная доходность очередного выпуска устанавливается равной

рыночной процентной ставке в день выпуска. Облигация имеет бесконечную продол-

жительность, т. е. она никогда не будет погашена с выплатой 1000 долл. Такая обли-

гация действительно существует; она называется консоль (consol) и выпускается

британским правительством.

Теперь предположим, что 1 января^ рыночная процентная ставка в рассматриваемой

экономике составляет 10%. Консоль, которую вы можете получить, если отдадите пра-

вительству 1000 долл., имеет большое (бесконечно большое!) число купонов, один из

которых вы можете погасить в конце года, получив доход в размере 100 долл. Иными

словами, вы в конце года высылаете по почте свой купон и через некоторое время

получите, и также по почте, 100 долл. Номинальная доходность облигации равна 10%

годовых. Допустим, что к началу следующего года рыночная процентная ставка подня-

лась с 10 до 20%. И предположим, что вы решили продать консоль

января следую-

щего года. Захочет ли кто-нибудь заплатить вам 1000 долл. за эту облигацию с ее

купонным доходом

10%.'^

Пожалуй, нет. Ведь каждый может купить облигацию нового

выпуска с доходностью 20% годовых, поскольку, согласно нашему предположению,

правительство осуществляет каждую новую эмиссию исходя из текущей рыночной про-

центной ставки. Какова максимальная цена, которую вы можете получить за облига-

цию.-^

Вы должны дать покупателю нечто сравнимое с тем, что он получит, купив новую

облигацию. Поэтому за купонный доход 100 долл. в год в экономике с процентной

ставкой 20% вы получите лишь 500 долл. (100 долл. равно 20% от 500 долл.).

Этот простой пример иллюстрирует важнейший вывод, который используется, далее,

во всей этой книге:

Рыночная цена существующих (старых) облигаций обратно прогюрциональна

рыночной процентной ставке в экономике.

Существует простая формула, описывающая консоль, т. е. облигацию с бесконеч-

ной «продолжительностью» (без срока погашения). Цена консоли с доходом в 1 долл.

в год равна 1 долл., деленному на г, где г — рыночная (номинальная) процентная

ставка (в десятичной форме записи). Это можно представить, как

Цена консоли с доходом в 1 долл. = 1 долл./л

В общем, если R — ежегодный купонный доход, а г — процентная ставка, цена

облигации равна R/r. В нашем примере, следовательно, R = \ долл.

ГЛАВА 7

Процентные ставки 159

В приведенном выше примере сумма, выплачиваемая ежегодно, равнялась 100 долл.

При рыночной процентной ставке 10% по указанной формуле рыночная цена облига-

ции будет 100 долл., деленным на 0,10, или 1000 долл. При рыночной процентной

ставке 20% по той же формуле цена облигации равна 100 долл., деленным rta 0,20,

т. е. 500 долл. Таким образом, даже в отсутствие риска при выплате процентов (или

при выплате основной суммы для облигации определенной «продолжительности», т. е.

со сроком погашения) нельзя бьп'ь уверенным в том, что рьшочная цена существующей

облигации будет оставаться такой, за которую она куплена. Когда процентные ставки в

экономике растут, цены на существующие облигации будут падать, потому что облига-

ция, по определению, есть актив, доходность которого является фиксированной ежегод-

ной суммой. Наоборот, если процентные ставки падают, рьшочные цены на существу-

ющие облигации растут. Иными словами, владельцы облигаций имеют капитальный

убыток или прирост капитала из-за изменения рьшочной цены таких активов.

На рис. 7-9 приведены графики спроса и предложения консолей; как и рис. 7-8, он

аналогичен рис. 7-3. На рис. 7-9 показана цена бессрочной облигации, приносящей

ежегодно 50 долл. ее владельцу. При цене 500 долл., что эквивалентно доходности

10%,

существует равновесие. При более низкой цене существует недостаточное предло-

жение консолей (соответствующее избыточному предложению кредита; рис. 7-3), из-за

которого цены на консоли будут расти, а процентные ставки падать. При цене, более

высокой, чем 500 долл., возникает избьггочное предложение консолей и недостаточное

предложение кредита, из-за чего цены на консоли падают и процентные ставки растут.

Цена

консоли,

$625

$500

$416,67

Число консолей

единицу времени

Рис. 7-9

Спрос и предложение консолей. На этом

рисунке показаны кривые спроса и предложе-

ния консолей с доходом 50 долл. в год. Рав-

новесие существует при цене 500 долл., что

эквивалентно рыночной процентной ставке

10%.

При цене консоли 625

долл.,

эквивалент-

ной процентной ставке 8%, возникает избы-

точное предложение консолей и недостаточ-

ное предложение кредита. При цене консоли

416,67 долл. возникает недостаточное предло-

жение консолей и избыточное предложение

кредита. На конкурентном рынке колебания

спроса и предложения взаимно погашаются, и

цена консоли устанавливается на уровне

500

долл.,

что соответствует цене равновесия.

ИЗМЕНЕНИЯ ПРОЦЕНТНОЙ СТАВКИ И ЦЕНЫ ОБЛИГАЦИИ

Почему между ценой облигации и ее доходностью при фиксированной купонной вы-

плате существует обратно пропорциональная зависимость, станет ясно, если вспом-

нить уравнение (7-1):

Р = V(l +'•) +^2/(1+'-)' + V(l +'•)' + - + /?„/(!+/-)"•

Для облигаций все R — константы. Если г растет, то Р будет падать; если г падает,

то Р растет.

В этой главе мы рассчитывали доходности и цены облигаций. Рассмотрим табл. 7-2,

в которой приведены различные рыночные процентные ставки и соответствующие

цены облигаций с различными сроками погашения. И для 3-летних облигаций, и для

консолей купонный доход равен 50 долл. в год. Отметим, что определенное изменение

160 ЧАСТЬ II Финансовые инструменты, рынки и институты

процентной ставки приводит

гораздо меньшему изменению цены 3-летней» облига-

ции, чем цены консоли.

ТАБЛИЦА 7-^2

Рыночная процентная ставка, % Цена 3-летней облигации Цена консоли

12 831,87 долл. 416,67 долл.

10 875,65 долл. 500,00 долл.

8 922,69 долл. 625,00 долл.

В следующем разделе, рассматривая доходности краткосрочных облигаций (вексе-

лей),

мы снова убедимся в том, что чем меньше срок погашения облигации, тем мень-

ше изменения ее цены при данном изменении рыночной процентной ставки.

Облигации могут приносить своим владельцам прирост капитала или капитальный

убыток. Более того, облигации

более длительными сроками погашения приносят

больший прирост капитала или капитальный убыток, чем краткосрочные при данном

изменении процентных ставок. Из этого важного вывода следует, что долгосрочные

облигации менее ликвидны, чем краткосрочные. Последний вывод чрезвычайно ши-

роко используется

последующих главах.

РАСЧЕТ ПУБЛИКУЕМЫХ ПРОЦЕНТНЫХ СТАВОК

ПО КАЗНАЧЕЙСКИМ ВЕКСЕЛЯМ

Публикуемые процентные ставки по казначейским векселям (Treasury bill rates) —

это ставки дисконта, вычисленные на основании 360-дневного года (такая длитель-

ность года принята для упрощения расчетов). Рассмотрим следующий пример: казна-

чейский вексель номиналом 10 000 долл. со сроком погашения через 91 день прода-

ется на аукционе за 9685 долл. Процентная ставка по векселю рассчитывается по

следующей формуле:

r^=[(F-P)/F\x(36Q/n),

(7-3)

где г^ — процентная ставка по векселю;

F — номинал;

Р — цена;

—

число дней до погашения.

В нашем примере

г^ = [(10 000 долл.

9 685 долл.)/10 000 долл.] X (360/91).

(7-4)

Поэтому Казначейство выставит такой вексель на аукционе по ставке 12,462%.

Расчет эквивалента купонного дохода по казначейским векселям Публикуемые

процентные ставки по казначейским векселям основаны на 360-дневном годе и номи-

нальной стоимости векселя. Эквиваленты купонного дохода основаны на 365-дневном

годе и рыночной цене векселя. Для вычисления эквивалента купонного дохода (coupon

yield equivalent), или аппроксимации фактического годового дохода, следует подста-

вить

уравнение (7-3) длительность года (365 дней) и фактическую цену покупки

казначейского векселя в начале периода. Формула для вычисления аппроксимирован-

ного купонного дохода такова:

r=[(F-P)/P]x(365/n).

(7-5)

ГЛАВА 7 Процентные ставки

161

Здесь г у — аппроксимированный купонный доход;

— цена казначейского ве1:сселя;

п — число дней до погашения. Член

—

Р)/Р

выражает процентную ставку за

период,

член 365/п выражает число периодов

году. Умножая первый член на

второй, получаем годовую процентную ставку; таким образом, можно сравнивать до-

ходность краткосрочных и долгосрочных бумаг, откуда

появился термин «эквива-

лент». Рассчитанная таким образом доходность рассматривается как «аппроксимиро-

ванная» годовая ставка, потому что ее вычисление предполагает, что за все периоды

рыночные условия не изменятся, что, конечно, мало вероятно.

В рассмотренном выше примере 91-дневного казначейского векселя номиналом

10 000 долл. и с продажной ценой 9685 долл., используя упрощенную формулу имеем:

г^ = [(100

96,85)796,85]

(365/91)

0,13046.

(7-6)

Купонный доход такого казначейского векселя равен 13,046%. Эта величина выше

публикуемой процентной ставки, потому что в ней учтены: 1) фактическое число дней

в году;

тот факт, что доход рассчитывается, исходя из фактически затраченной

суммы (цены покупки),

не из номинальной цены казначейского векселя.

ВТОРИЧНЫЙ РЫНОК КАЗНАЧЕЙСКИХ ВЕКСЕЛЕЙ

Казначейские векселя активно торгуются на вторичном рынке, потому что некоторые

покупатели (домашние хозяйства, фирмы, банки, ФРС) предпочитают продавать свои

91-дневные (или другие) векселя до срока погашения. Этот вторичный рынок делает

казначейские векселя самым ликвидным финансовым активом, уступающим по лик-

видности только деньгам. Существуют дилеры, специализирующиеся по государст-

венным ценным бумагам, которые готовы покупать казначейские векселя или прода-

вать их кредиторам

любой момент.

Эти дилеры собирают информацию

ценах продавца и покупателя (ставках дис-

конта) торгуемых векселей. Эти ставки дисконта — не то же самое, что рассмотрен-

ный выше аппроксимированный купонный доход, который представляет собой ставку

ценной бумаги на первичном рынке. Они выступают средством определения цены, по

которой казначейские векселя будут торговаться на вторичном рынке. Для примера

рассмотрим казначейский вексель со сроком погашения 73 дня. Цена продавца этой

ценной бумаги

—

96,785. Это означает, что покупатель должен отдать дилеру

9678,50 долл. В свою очередь покупатель получит казначейский вексель номиналом

10 000 долл., который будет погашен через 73 дня. Формула для расчета аппрокси-

мированного купонного дохода:

r^=[{F-P)/P]x(365/n).

(7-7)

где,

как

раньше,

— цена продавца,

an —

число дней до срока погашения.

Отметим, что теперь, поскольку мы ведем расчет не для первичного рынка, то

А2

—

не обязательно 91 или 282 дня; это число дней, оставшихся до срока погашения

рассматриваемого векселя.

Доходность при погашении этого казначейского векселя рассчитывается, как

г^= [(10 000 долл.

9678,50 долл.)/9678,50] х (365/73) = 0,16608. (7-8)

Поэтому аппроксимированный купонный доход составляет 16,608% годовых. Эта

цифра представляет собой аппроксимированный годовой доход покупателя, который

приобретает этот вексель, хранит его до срока погашения (73 дня)

получает от

Казначейства США 10 000 долл. при погашении векселя. С другой стороны, прода-

вец получает доход

размере 16,608% годовых, продав вексель.

162 ЧАСТЬ II Финансовые инструменты, рынки и институты

Ликвидность

казначейские векселя Отметим, что аппроксимированный купонный

доход по казначейским векселям на вторичном рынке не связан какой-то однозначной

зависимостью ни

объявленным доходом после продажи векселей на аукционе, ни

аппроксимированным купонным доходом в день аукциона. Если соотношение спроса и

предложения новых казначейских векселей, проданных на рынке, резко меняется, экви-

валент купонного дохода на вторичном рьшке может значительно отличаться от дохода

в день выпуска. Однако, чем меньше срок казначейского векселя, тем меньше меняется

фактическая цена этого векселя на вторичном рынке при данном изменении процентных

ставок

экономике. В конце концов для проданного на аукционе 91-дневного векселя

до срока погашения остается всего 90 дней. Даже если общий уровень проценггных

ставок в экономике резко повышается, скажем, через 10 дней после продажи казначей-

ского векселя, его цена на вторичном рынке незначительно упадет, поэтому его владель-

цу надо просто подождать 81 день, чтобы обменять поступления от продажи казначей-

ского векселя на более доходный актив.

Для прояснения этого вопроса рассмотрим крайний случай. Предположим, что

через день после того, как на аукционе было продано большое число казначейских

векселей

эквивалентом купонного дохода 10%, все процентные ставки

экономике

удвоились. Напомним, что в такой ситуации рыночная цена торгуемых консолей упала

бы вдвое по сравнению

их ценой

день выпуска. Что случится

рыночной ценой

казначейского векселя, которому остается до погашения, скажем, 90 дней? Опреде-

лим сначала их цену

день выпуска,

затем цену на следующий день. Если эти

казначейские векселя имели фактический купонный доход 10%

день выпуска, их

цена

этот день могла быть определена по формуле:

r^={{F-P)/P\xO(>Vn).

(7-9)

Отсюда

можно выразить, как

Р = Р/[{ГуХ п/Ъв5)

1].

(740)

Поэтому

10 000 долл.ДОДО (91/365)

1]. (7-11)

Итак,

Р = 9756,75 долл.

Иными словами, при продаже 91-дневный казначейский вексель номиналом 10 000 долл.

имеет рыночную цену 9756,75 долл.

Если за ночь все процентные ставки удваиваются, вчерашний выпуск казначейских

векселей будет продаваться на вторичном рынке по цене, отражающей новую рыноч-

ную конъюнктуру. Эквивалент купонного дохода составит теперь 20%. Рассчитаем

цену казначейских векселей, проданных вчера, до погашения которых осталось 90 дней.

Подставляя новые величины

уравнение (7-10), получим:

10 000 долл./[0,20 (90/365)

1]. (7-12)

Поэтому

9530,03 долл.

Рыночная цена казначейского векселя упадет с цены в момент выпуска 9756,75 долл.

до 9530,03 долл. на следующий день. Уменьшение цены составило только 2,3%, хотя

процентные ставки удвоились.

ГЛАВА 7 Процентные ставки 163

Теперь рассчитаем изменение рыночной цены 5-летней облигации в случае удвоения

процентных ставок. Возвращаясь к уравнению (7-1), по которому рассчитывается цена

долгосрочных облигаций, мы найдем, что в момент выпуска, при процентной ставке

10%,

5-летняя облигация с номинальной доходностью 5% и номиналом 10 000 долл.

будет стоить:

/> = 500долл./1,1 +500долл./(1Д)^ + 500долл./(1,1)^ -f

+ 500долл./(1Д)Ч

500дoлл./(lД)^ (7-13)

Отсюда

Р= 454,55 + 413,22 + 375,66 + 341,51 + 6519,7 = 8104,61 (долл.).

Если процентные ставки удваиваются, т. е. становятся равными 20%, эта облигация

будет продаваться по цене

Р = 500/1,2 +500/(1,2)^ + 500/(1,2)^ + 500/(1,2) V Ю 500/(1,2)^ =

= 416,67 + 347,22 + 289,35 + 241,12 + 4219,71 = 5514,07 (долл.).

Цена этой облигации упадет с 8104,61 до 5514,07 долл. Если вы купите вновь

выпущенную 5-летнюю облигацию с 5-процентной номинальной доходностью, а на сле-

дующий день процентные ставки удвоятся, то облигация будет стоить на 2590,59 долл.

меньше, чем за день до повышения ставок: уменьшение цены составит 31,96%.

Этот результат подтверждает сделанный ранее вывод. Чем меньше срок до пога-

шения облигации или векселя, тем меньше изменяется их цена при определенном из-

менении рыночных процентных ставок. Казначейские векселя необычайно ликвидны

потому, что имеют малую продолжительность и соответственно их рыночные цены

относительно нечувствительны к изменениям процентных ставок. Кроме того, они

свободно торгуются на вторичнол* рынке.

Расчет различных процентных ставок

Теперь вы знаете, что существует много различных видов облигаций и что их доход-

ность часто значительно различается. В этом разделе мы покажем, что эти отличия

объясняются тем, что облигации имеют:

1) различный уровень кредитного риска;

2) различную ликвидность;

3) различные условия налогообложения;

4) различные сроки погашения.

Для упрощения анализа экономисты рассматривают разные виды процентных ста-

вок при таких допущениях:

Предполагают срок погашения одинаковым и рассматривают зависимость доход-

ности по облигациям: а) от кредитного риска; б) от ликвидности; в) от налогооб-

ложения. Такой общий подход обычно называют рисковой структурой процент-

ных ставок {risk structure of interest rates).

Предполагают одинаковыми кредитный риск, ликвидность и налогообложение и

изучают дифференциацию доходности в зависимости от срока погашения. Это назы-

вается временной структурой процентных ставок (term structure of interest rates).

164 ЧАСТЬ II Финансовые инструменты, рынки и институты

РИСКОВАЯ СТРУКТУРА ПРОЦЕНТНЫХ СТАВОК

Облигации с одинаковым сроком погашения имеют разную доходность, если, как уже

указывалось, они характеризуются разным уровнем риска, ликвидностью и налогооб-

ложением.

Различия в уровне кредитного риска Рассмотрим две облигации (Аи В),у которых

все одинаково; у них одна и та же ликвидность, срок погашения, уровень кредитного

риска, они облагаются одинаковым налогом и т. д. В такой ситуации облигации будут

иметь одну и ту же рыночную цену Р; поскольку купонные выплаты по ним одинако-

вы,

их доходность будет одинаковой. Предположим теперь, что корпорация Д выпу-

стившая облигацию В, столкнулась с финансовыми или экономическими трудностями

и рейтинговые агентства снизили рейтинг облигаций корпорации В. Поскольку теперь

кредитный риск по облигации В выше, чем по облигации Л, спрос на облигацию В

упадет, что приведет к снижению цены на эту облигацию и к росту ее доходности. В

то же время возрастает спрос на облигацию А, что приведет к росту ее цены и сни-

жению доходности. Иными словами, возникнет спрэд (разница) в доходности обли-

гаций А и В, представляющий собой премию за риск.

Отметим, что доходность облигации В будет выше доходности облигации Л, пото-

му что купонные выплаты по облигациям одинаковы, но цена облигации А выше цены

облигации В. С другой точки зрения, это можно представить так: поскольку уровень

риска по облигации В выше, инвесторы требуют большего процентного дохода по ней.

Цены облигаций будут изменяться до тех пор, пока спрэд в доходности не станет

соответствовать разнице в степени риска. Мы приходим к заключению, что разные

облигации имеют различную доходность, в частности, потому что уровень риска по

ним неодинаков.

Различия в ликвидности Вновь рассмотрим две облигации (Си/)), одинаковые во всех

отношениях. Предположим, что облигация D стала более ликвидной, например, потому

что торговля ею организована более широко. Повторяя предыдущие рассуждения, мы

приходим к заключению, что спрос на облигацию D растет, а на облигацию С — падает

и что цена облигации D падает, а цена облигации С

растет.

(Напомним, что если купонный

доход по облигациям одинаков, а цены различны, то их доходность различна.)

Можно сделать вывод, что, если разные облигации различаются ликвидностью,

они будут приносить разную доходность. Конкретнее, облигации, ликвидность кото-

рых выше, при прочих равных условиях будут приносить меньшую доходность, чем

облигации, ликвидность которых ниже. Иначе говоря, инвесторы требуют более низ-

кую процентную ставку по более ликвидным облигациям при прочих равных условиях.

Проведенный анализ объясняет, почему государственные ценные бумаги США

более ликвидны, чем корпорационные облигации (рынок облигаций частных корпора-

ций значительно «тоньше», чем рынок государственных ценных бумаг), и имеют от-

носительно низкую доходность. Конечно, государственные ценные бумаги США про-

даются по низкой процентной ставке еще и потому, что они имеют чрезвычайно низ-

кий кредитный риск.

Различия в налогообложении В продаже имеются ценные бумаги, не облагаемые

налогом. Величина не облагаемого налогом дохода по муниципальным облигациям

прямо пропорциональна размеру предельной ставки налога. В 1991 г. в федеральном

налогообложении личных доходов существовало три ставки налога: 15, 28 и

31%,

хотя

с учетом различных вычетов и налоговых льгот фактическая предельная ставка налога

для отдельных категорий налогоплательщиков может доходить до 35%. Размер необ-

лагаемой части дохода меньше для тех, кто платит налоги по ставке 15%, чем для тех,

кто их выплачивает по ставке 31%.

ГЛАВА 7 Процентные ставки

165

На рынке индивиды, принадлежащие к налоговой категории, облагаемой по более

высокой ставке, устанавливают такую цену на не облагаемые налогом муниципальные

облигации, что их доходность падает ниже доходности эквивалентных, но облагаемых

налогом облигаций. В предельном случае фактическая доходность не облагаемых на-

логоми облигаций зависит от предельной налоговой ставки, по которой облагается

маржинальный покупатель таких облигаций. Таким образом, каждый покупатель об-

лигаций, не облагаемых налогом, платит неявный налог, представляющий собой раз-

ность между доходностью муниципальной облигации и доходностью эквивалентной

корпорационной облигации. Приобретение не облагаемых налогом облигаций позволя-

ет инвестору избежать только явного налогообложения.

Процент

8,0

7,5

7,0

6,5

6,0

5,5

5,0

4,5

4,0 Ь

3,5

Доходность по состоянию на 16.30

(по восточному времени)

Вчера

Неделю назад

4 недели назад

Месяцы

Годы

5 7 10

Срок погашения

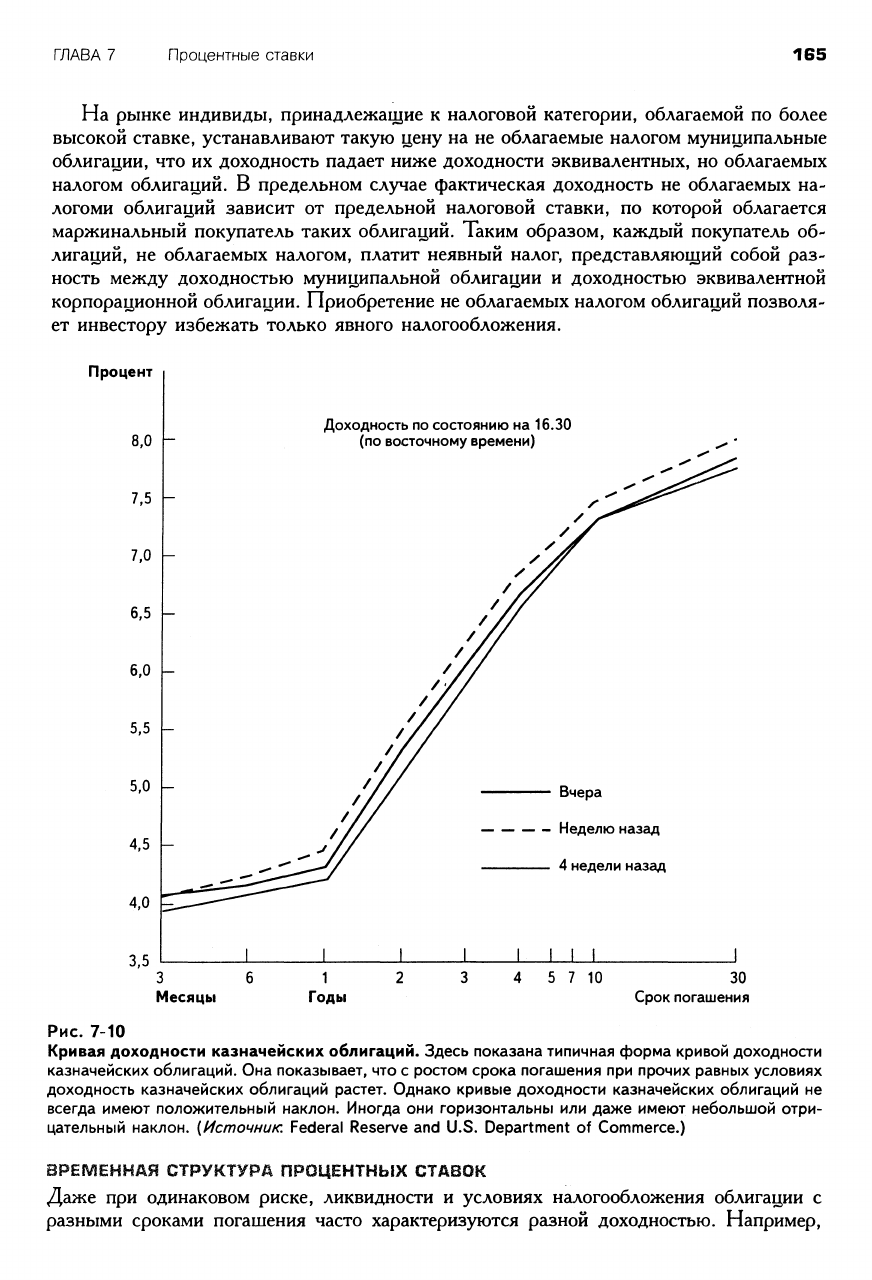
Рис. 7-10

Кривая доходности казначейских облигаций. Здесь показана типичная форма кривой доходности

казначейских облигаций. Она показывает, что с ростом срока погашения при прочих равных условиях

доходность казначейских облигаций растет. Однако кривые доходности казначейских облигаций не

всегда имеют положительный наклон. Иногда они горизонтальны или даже имеют небольшой отри-

цательный наклон. (Источник. Federal Reserve and U.S. Department of Commerce.)

ВРЕГ^^ЕННАЯ СТРУКТУРА ПРОЦЕНТНЫХ СТАВОК

Даже при одинаковом риске, ликвидности и условиях налогообложения облигации с

разными сроками погашения часто характеризуются разной доходностью. Например,