Методичні вказівки до виконання лабораторних робіт з дисципліни Теорія автоматичного керування
Подождите немного. Документ загружается.

Приклади технологічних об’єктів
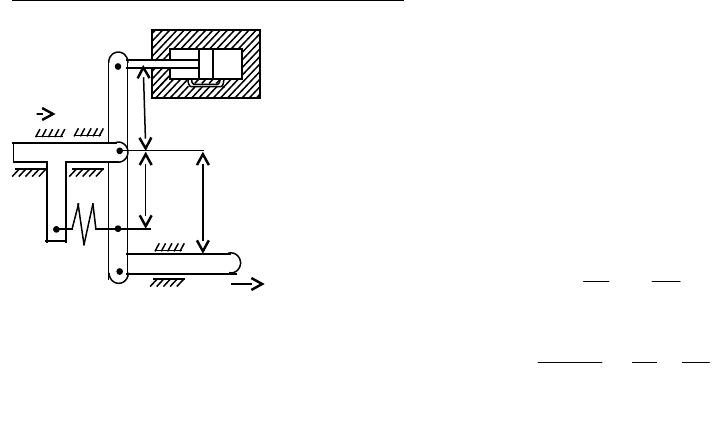
Ізодром з важільною системою (Рис. 4.11).
Вхідні та вихідні параметри ланки вказані
на малюнку.
Коефіцієнт передачі для даного пристрою:
1k
Постійні часу визначаються за формулами
наступним чином:
k
T
2
2
1
1
k
T
2
2
1
31
1
2
,
де ℓ
1
, ℓ
2
, ℓ
3
– довжини плеч важелів, м;
– коефіцієнт в’язкого тертя,
Н·с/м
2
.
Приклади
Чотирьохполюсники (фазо-випереджуючі)
51
x
вх
x
вих
ℓ
1
ℓ
2
ℓ
3
Рис. 4.11
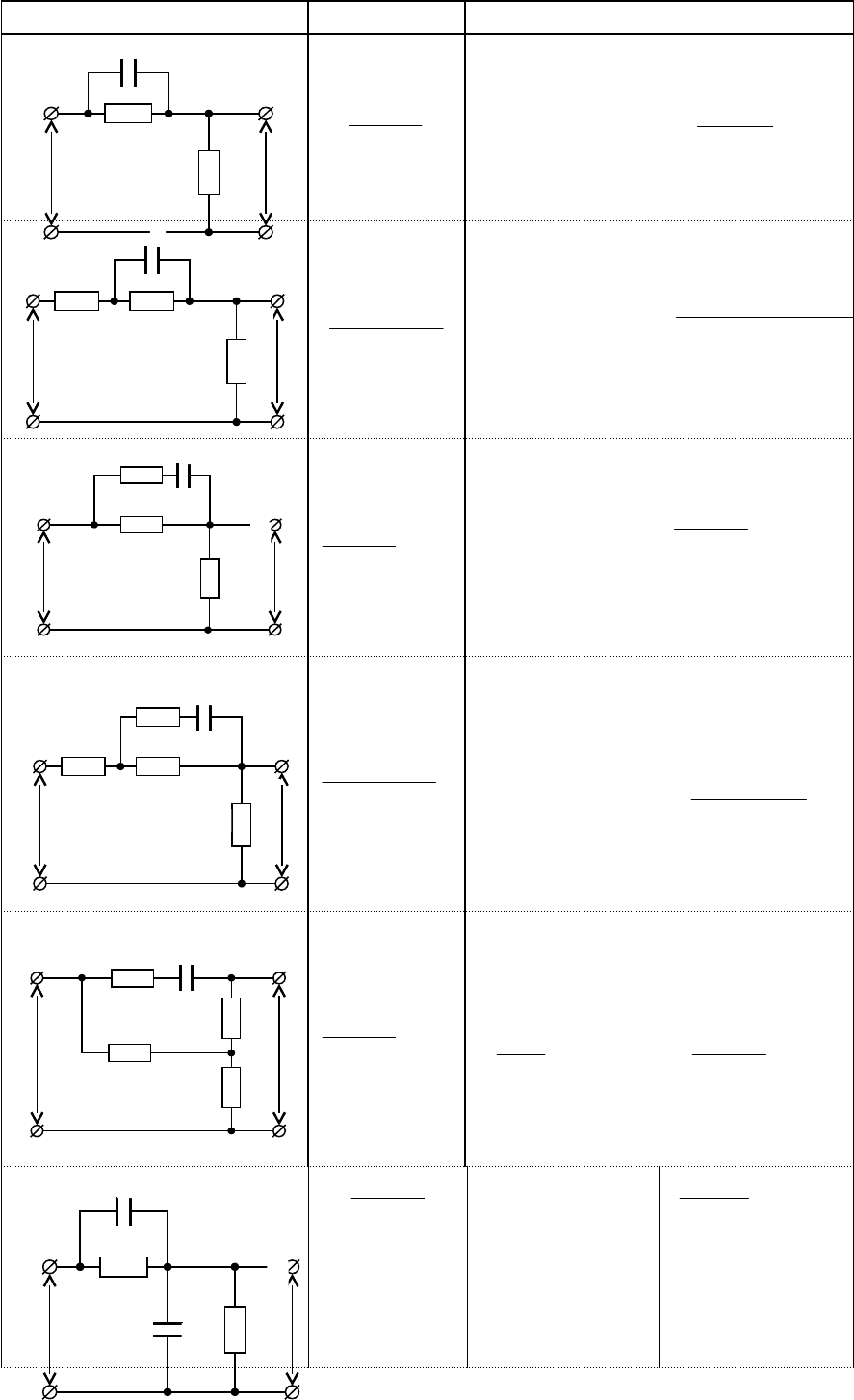
Схема K T
1
T
2
21
2
RR
R
CR
1
CR
RR
R
1
21
2
321
2
RRR
R
CR
1
CR
RRR
RR
1
321
32
21
2
RR
R
CRR
31
CR
C
RR
RR
3
21
21
321
2
RRR
R
CRR
41
C
RRR
R
RR
321
2
1
41
21
2
RR
R
C
R
RR
RRR
2
41
431
C
RR
RR
RR
21
21
43
21
2
RR
R
11
CR
21
21
21
CC
RR
RR
52
С
U
вх
R2
R1
U
вих
U
вх
U
вих
С
R1R3
R2
U
вх
U
вих
С
R4
R3
R1
R2
U
вх
U
вих
R3
R1
С
R2
U
вх
U
вих
R3
С
R1
R4
R2
U
вх
U
вих
С1
С1
R2
R1
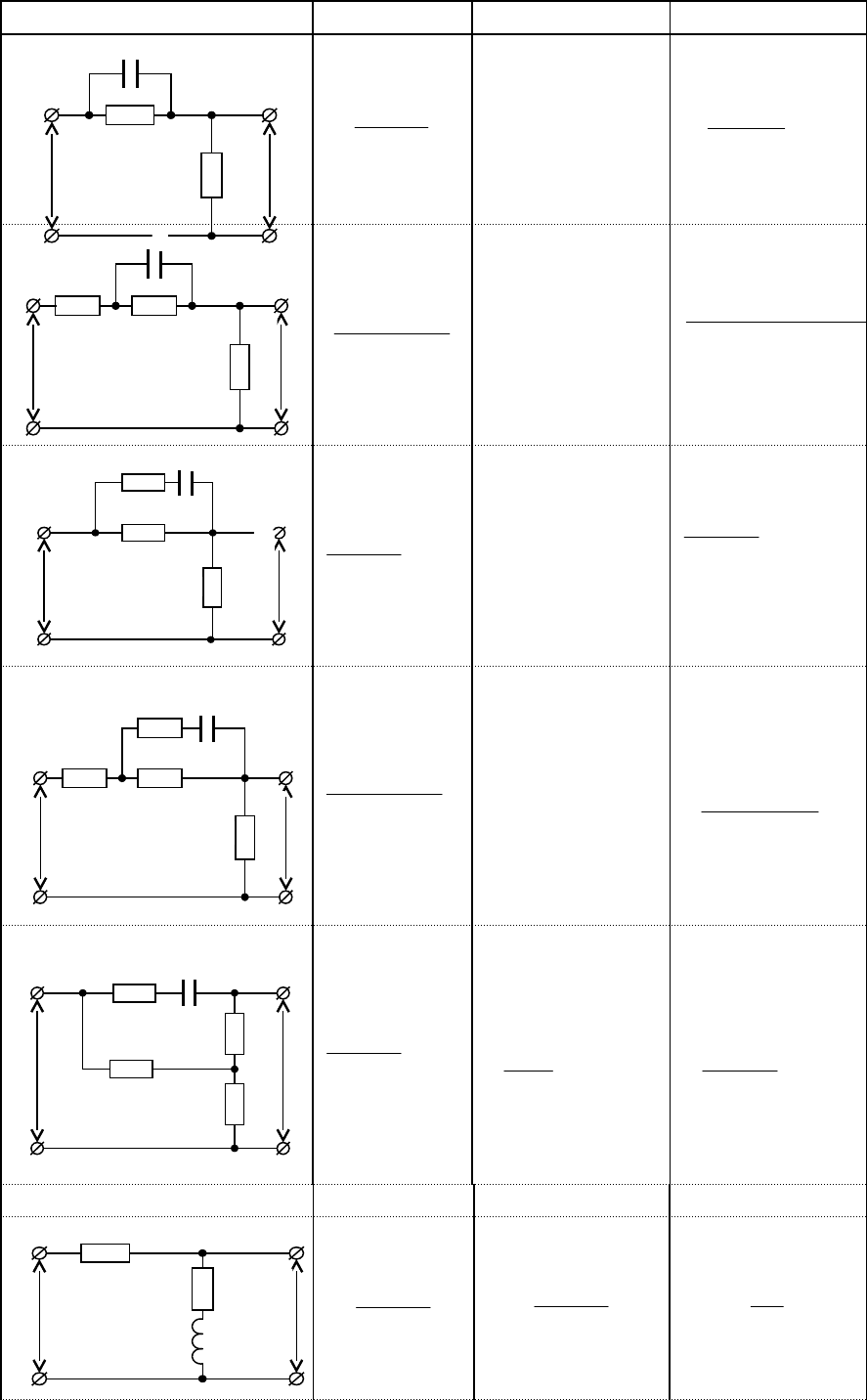
Схема K T
1
T
2
21
2
RR
R
CR
1
CR
RR
R
1
21
2
321
2
RRR
R
CR
1
CR
RRR
RR
1
321
32
21
2
RR
R
CRR
31
CR
C
RR
RR
3
21
21
321
2
RRR
R
CRR
41
C
RRR
R
RR
321
2
1
41
21
2
RR
R
C
R
RR
RRR
2
41
431
C
RR
RR
RR
21
21
43
21
2
RR
R
21
RR
L
2
R
L
53
С
U
вх
R2
R1
U
вих
U
вх
U
вих
С
R1R3
R2
U
вх
U
вих
С
R4
R3
R1
R2
U
вх
U
вих
R3
R1
С
R2
U
вх
U
вих
R3
С
R1
R4
R2
U
вх
U
вих
R2
С1
R1
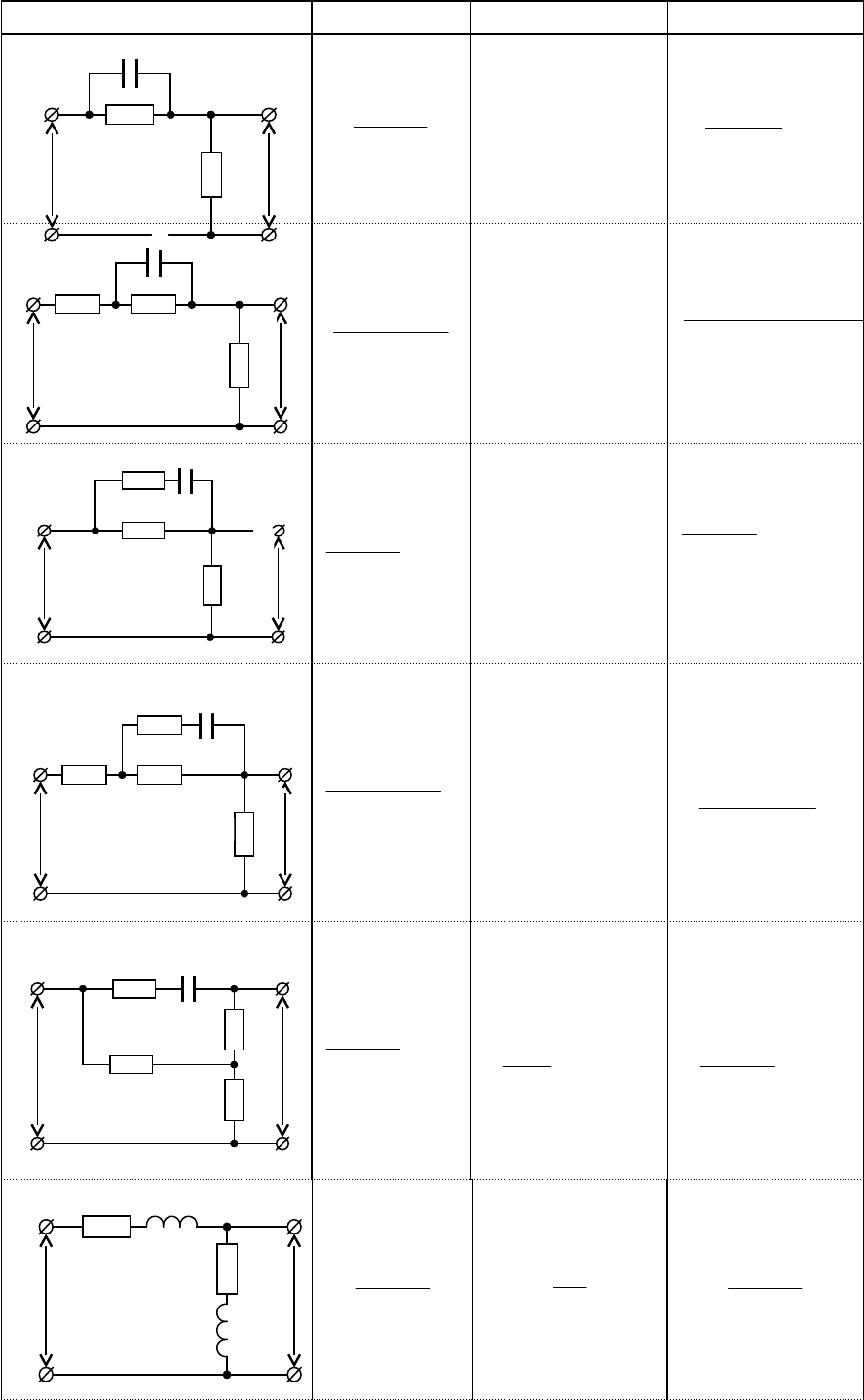
Схема K T
1
T
2
21
2
RR
R
CR
1
CR
RR
R
1
21
2
321
2
RRR
R
CR
1
CR
RRR
RR
1
321
32
21
2
RR
R
CRR
31
CR
C
RR
RR
3
21
21
321
2
RRR
R
CRR
41
C
RRR
R
RR
321
2
1
41
21
2
RR
R
C
R
RR
RRR
2
41
431
C
RR
RR
RR
21
21
43
21
2
RR
R
2
2
R
L
21
21
RR
LL
54
U
вх
U
вих
R1
R2
L1
U
ви
х
С
С
L2
С
U
вх
R2
R1
U
вих
U
вх
U
вих
С
R1R3
R2
U
вх
U
вих
С
R4
R3
R1
R2
U
вх
U
вих
R3
R1
С
R2
U
вх
U
вих
R3
С
R1
R4
R2
55
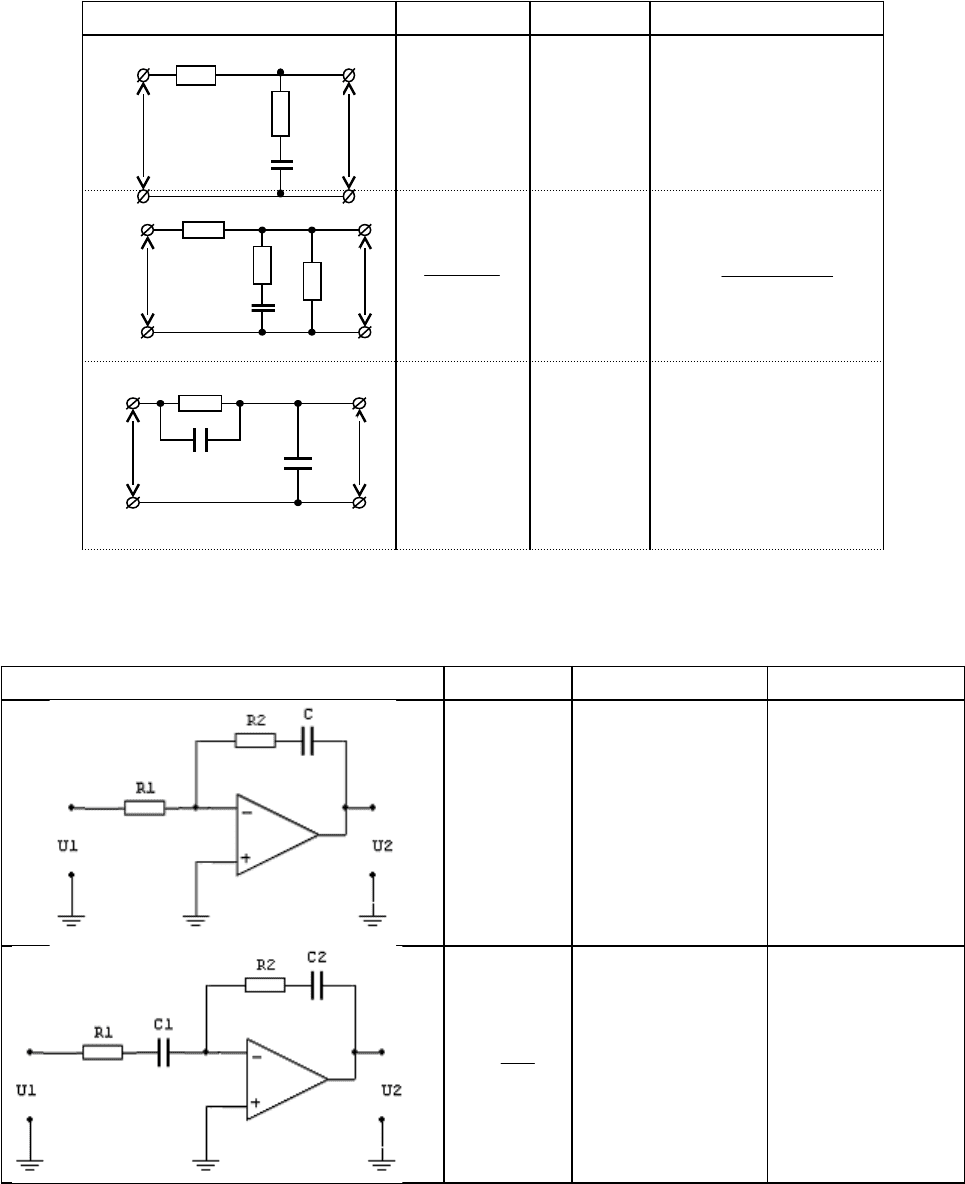
Чотирьохполюсники (фазо-відстаючі)
Схема K T
1
T
2
1
CR
2
CRR
21
31
3
RR
R
CR
2
C
RRR
RRR
R
231
321
2
1
1
RC
21
CCR
Чотирьохполюсники на активних елементах
Схема K T
1
T
2
-1
CR
2
CR
1
2
1
C
C
22
CR
11
CR
56
U
вх
U
вих
R1
R2
R1
U
вх
U
вих
R2
R3
C
R
С1
С2
U
вх
U
вих

Схема K T
1
T
2
1
2
R
R
CR
3
CRR
32
СИСТЕМА З ДВОХ АПЕРІОДИЧНИХ ЛАНОК 1-ГО
ПОРЯДКУ
Мета: зняти часові характеристики, виконати математичний
аналіз та провести ідентифікацію системи, що складається з двох
аперіодичних ланок 1-го порядку.
ВИХІДНІ ДАНІ ДЛЯ НАСТРОЮВАННЯ ПАРАМЕТРІВ СТЕНДУ СУЛ-
3
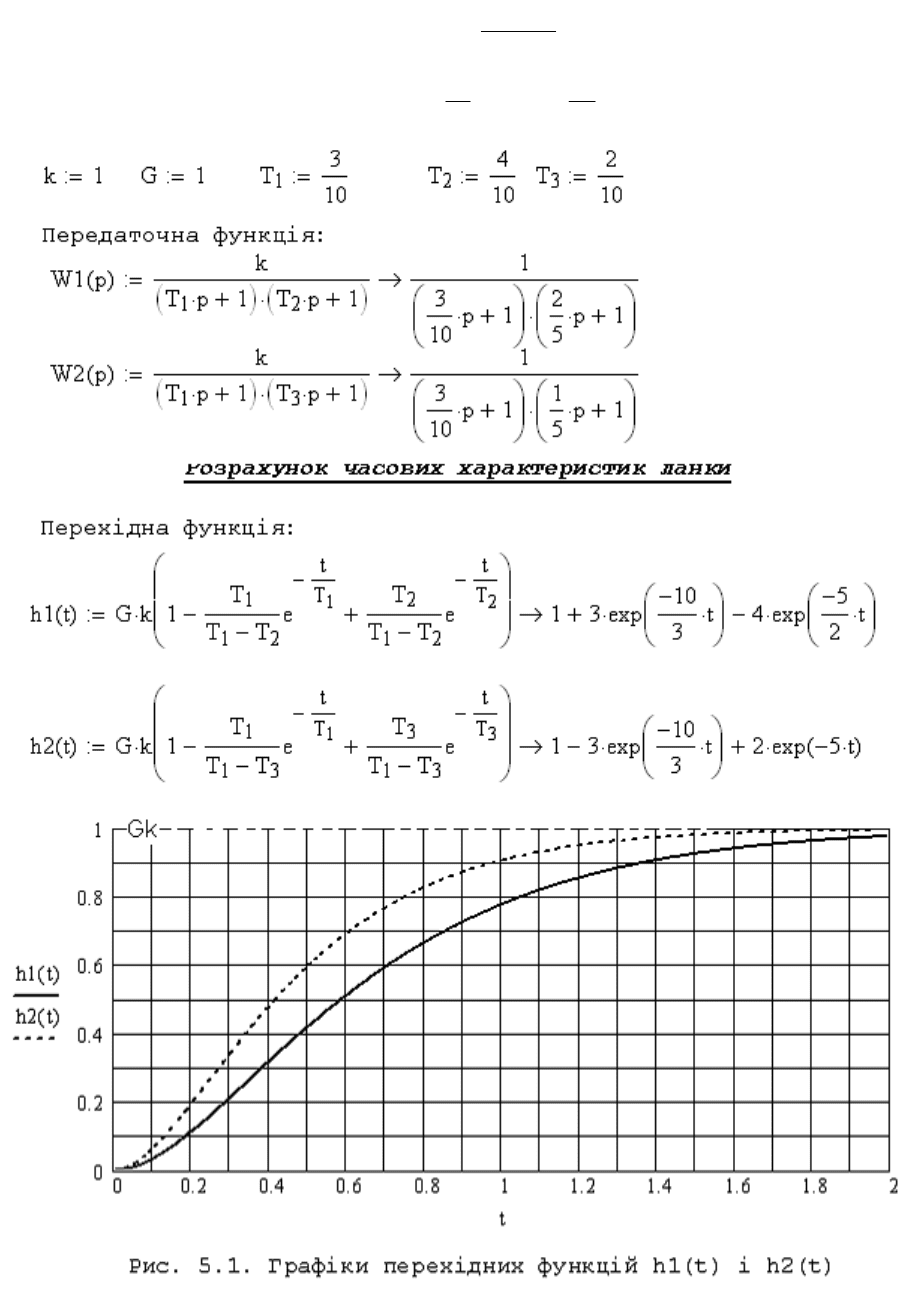
Вхідна напруга, В G 1
Коефіцієнт підсилення k 1
Перша постійна часу, с T
1
0,3
Друга постійна часу (1/2 варіант),
с
T
2
0,4 0,2
Постійна часу для ідентифікації, с T
X
T
X3
Передаточна функція має вигляд:
)1)(1(
)(
21
pTpT
k
pW
Диференційне рівняння ланки:
)()(
)()(
21
2
2
21
tkxty
dt
tdy
TT
dt
tyd
TT
57
)1)(1(
)(
21
pTpT
k
pW
X
Y

Легко бачити, що ланка з даною передаточною функцією може
розглядатися як послідовне з’єднання двох аперіодичних ланок: з
передаточними функціями
1
1
pT
k
і
1
1
2
pT
.
Із взаємної відповідності динамічних характеристик відомо, що
перехідна функція може бути знайдена як зворотне перетворення Лапласа
частки, діленим якої є передаточна функція, а дільником – оператор р.
Тобто:
p
pW
Lth
)(
)(
1
Знайдемо перехідну функцію. Для цього отриманий дріб розкладемо
методом невизначених коефіцієнтів на прості дроби:
)1)(()1)((
1
11
)(
221
2
2
121
2
1
21
рТТТ
Т
рТТТ
Т
р
k
рpTpT
k
p
pW
З таблиці зворотного перетворення Лапласа видно, що
)(1
0
0
1
ta
p
a
L
,
t
e
p
L
1
1
Перетворивши отриману формулу, знаходимо h(t):
2
21
2
1
1
21
1
11
221
2
2
121
2
1
1
1
1
)(
1
1
)(
1
)1)(()1)((
1
)(
T
p
ТТ
Т
L
T
p
ТТ
Т
L
p
Lk
рТТТ
Т
рТТТ
Т
р
kLth
або
21
21
2
21
1
1)(
T
t
T
t
e
ТТ
Т
e
ТТ
Т
kth
Знайдемо тепер імпульсну перехідну функцію. Як відомо, вона
представляє собою похідну від перехідної функції, тобто:
2121
2121
2
21
1
)()(
1
)(
)(
T
t
T
t
T
t
T
t
ee
TT
k
e
ТТ
Т
e
ТТ
Т
k
dt
d
dt
tdh
tw
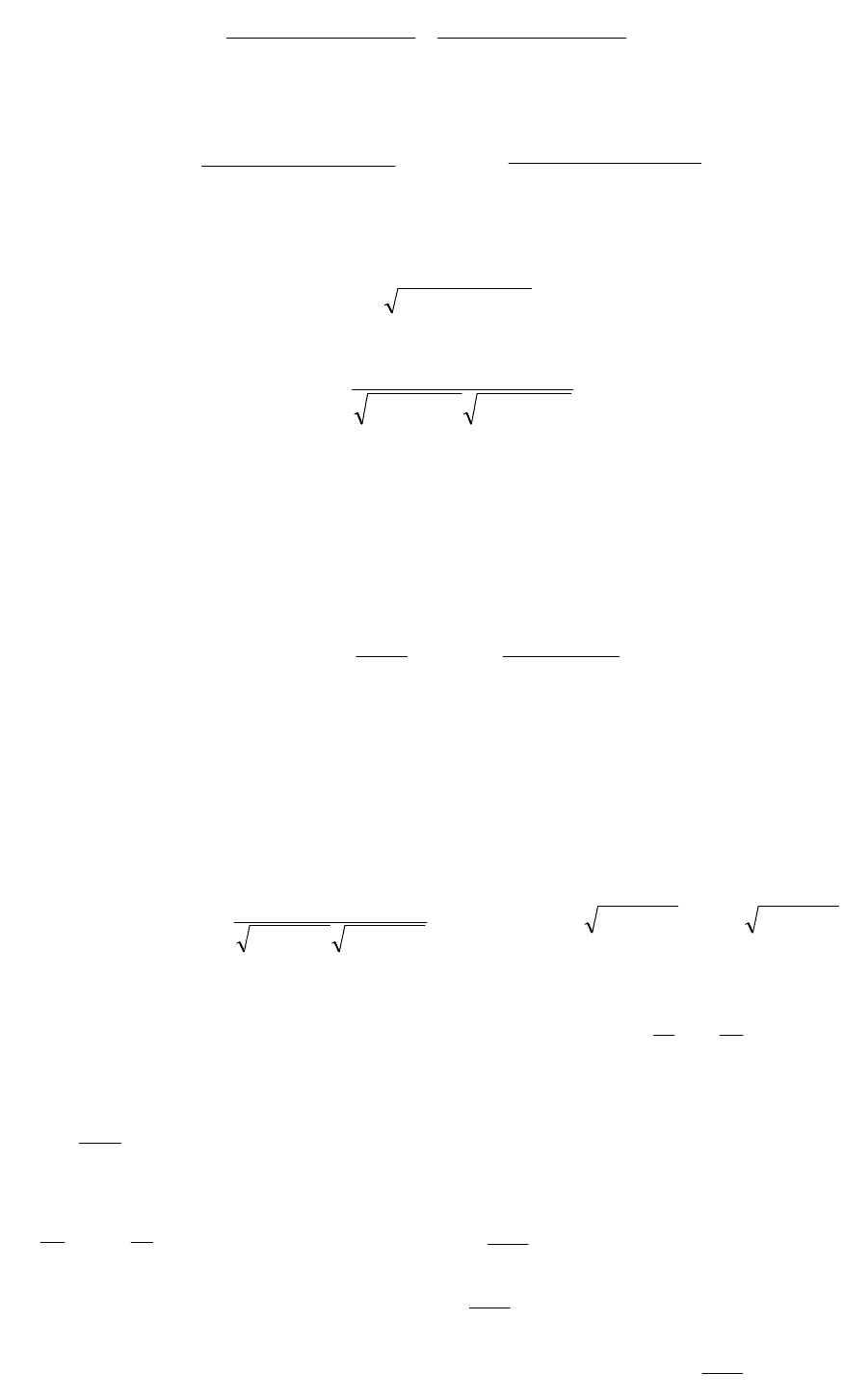
Амплітудно-фазова характеристика може бути отримана шляхом
підстановки в передаточну функцію
jp
.
)1(1
)(
21
jTjT
k
jW
22
21
22
21
21
2
21
)()1(
))(1(
TTTT
jTTTTk
58
j
TT
TTk
TT
TTk
1111
)1(
22
2
22
1
21
22
2
22
1
2
21
Звідси видно, що дійсна і уявна частотні характеристики дорівнюють
відповідно:
11
)1(
)(
22
2
22
1
2
21
TT
TTk
P
;
11
)(
22
2
22
1
21
TT
TTk
Q
.
Амплітудно-частотна характеристика представляє собою модуль
вектора амплітудно-фазової характеристики і знаходиться за формулою:
22
QPA
Підставивши в дану формулу вирази для
P
та
Q
, отримаємо:
A
=
11
22
2
22
1
TT
k
Проаналізувавши графік функції
A
, можна побачити, що дана
ланка має властивості фільтру низьких частот, тобто гармонічні сигнали
малої частоти пропускаються ланкою добре, а сигнали великої частоти
зазнають сильного ослаблення.
Фазочастотна характеристика може бути отримана за формулою:
)1(
2
21
21
TT
TT
arctg
P
Q
arctg
Чим більша частота вхідного сигналу, тим більше відставання по фазі
вихідного сигналу по відношенню до вхідного. Максимально можливе
відставання
180
.
Логарифмічна амплітудно-частотна характеристика описується
виразом:
1lg201lg20lg20
11
lg20lg20
22
2
22
1
22
2
22
1
TTk
TT
k
AL
Для знаходження асимптотичної логарифмічна амплітудно-частотної
характеристики, задамося умовою, що
21
12
1
lg
1
lg
TT
TT
. Перша
асимптота при
0
(
lg
) представляє пряму, що не має нахилу,
тобто
дек
Дб
0
:
kL lg20
1
,
при
12
11
TT
– пряму, яка має нахил
дек
Дб
20
:
2
2
lg20
T
k
L
а при
(
lg
) представляє пряму, яка має нахил
дек
Дб
40
:
59
2
21
3
lg20
TT
k
L
,
частоти спряження при цьому:
1
1
1
T
C
і
2
2
1
T
C
.
60
