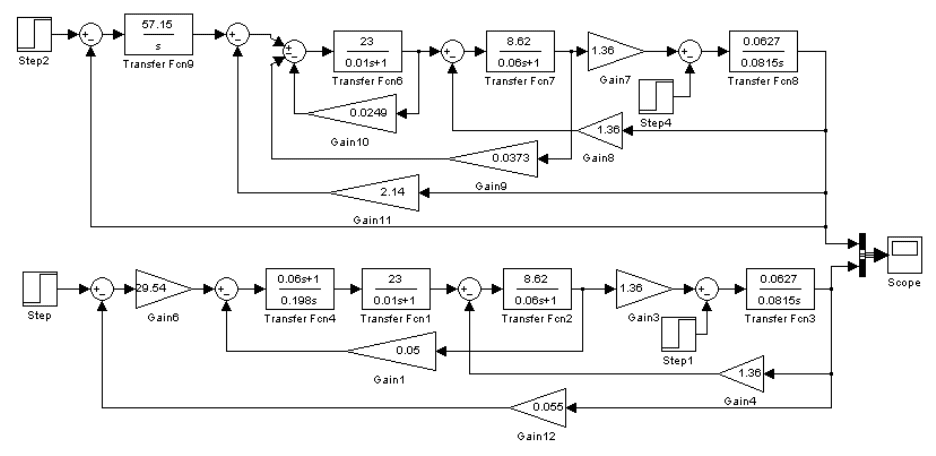
Методическое пособие

Подождите немного. Документ загружается.

Контрольные вопросы и задачи

Пример 13.1. Проверить свойство управляемости для объекта, модель

которого задана системой дифференциальных уравнений вида:

1 2

2 3

3 3 2 1

3 5 .

x x

x x x x u













   





Решение. Определим матрицу коэффициентов системы (А) и матрицу

входа (В)

0 1 0 1

0 0 1 ; 1

3 5 1 4

A B

   

   

  

   

       

   

Порядок системы равен 3, следовательно, матрица управляемости

имеет вид

 

Q B AB A B

Вычислим матрицы произведений

 

 



 

  

 

A B

 

 

 

 

  

 

Составим матрицу управляемости

0 0 1

0 1 1

1 1 4

 

 

 

 

   

 

ее определитель равен

det 1Q 

, следовательно, объект управляем.

13.1. Проверить свойство управляемости для объекта, модель которого

задана системой дифференциальных уравнений вида:

1 2

2 1 2

5 2 .

x x

x x x u







  





13.2. Проверить свойство управляемости для объекта, модель которого

задана системой дифференциальных уравнений вида:

1 2

2 1 2

2 ,

x x u

x x x u

y x

 





  











Найти передаточную функцию модели объекта, вычислить нули и полюса.

13.3. Проверить свойство управляемости для объекта, модель которого

задана системой дифференциальных уравнений вида:

1 1 2

2 1 2

1 2

3 .

x x x u

y x x

  





  





 





Найти передаточную функцию модели объекта, вычислить нули и полюса.

13.4. Проверить свойство управляемости для объекта, модель которого

задана системой дифференциальных уравнений вида:

1 1 2

2 2 3

1 3

2 .

x x x u

x x x

y x x u

  





 





  





13.5. Модель объекта управления задана передаточной функцией:

2 1

( ) .

5 6

W p

p p





 

Записать уравнения модели в форме Коши, проверить свойство

управляемости.

13.6. Модель объекта управления задана передаточной функцией:

( ) .

3 2

W p

p p





 

Записать уравнения модели в форме Коши, проверить свойство

управляемости.

13.7. Уравнения состояний системы имеют вид:

1 1 2

2 2 3

3 1 3

4 2 ,

5 ,

x x x u

y x

  





  





  









Проверить свойство управляемости объекта.

13.8. Модель объекта описывается передаточной функцией:

3 2

( ) .

4 3 5

W p

p p p



  

Проверить управляемость объекта.

13.9. Модель объекта описывается передаточной функцией:

( ) .

5 1

W p

p p U

 

 

Проверить управляемость объекта.

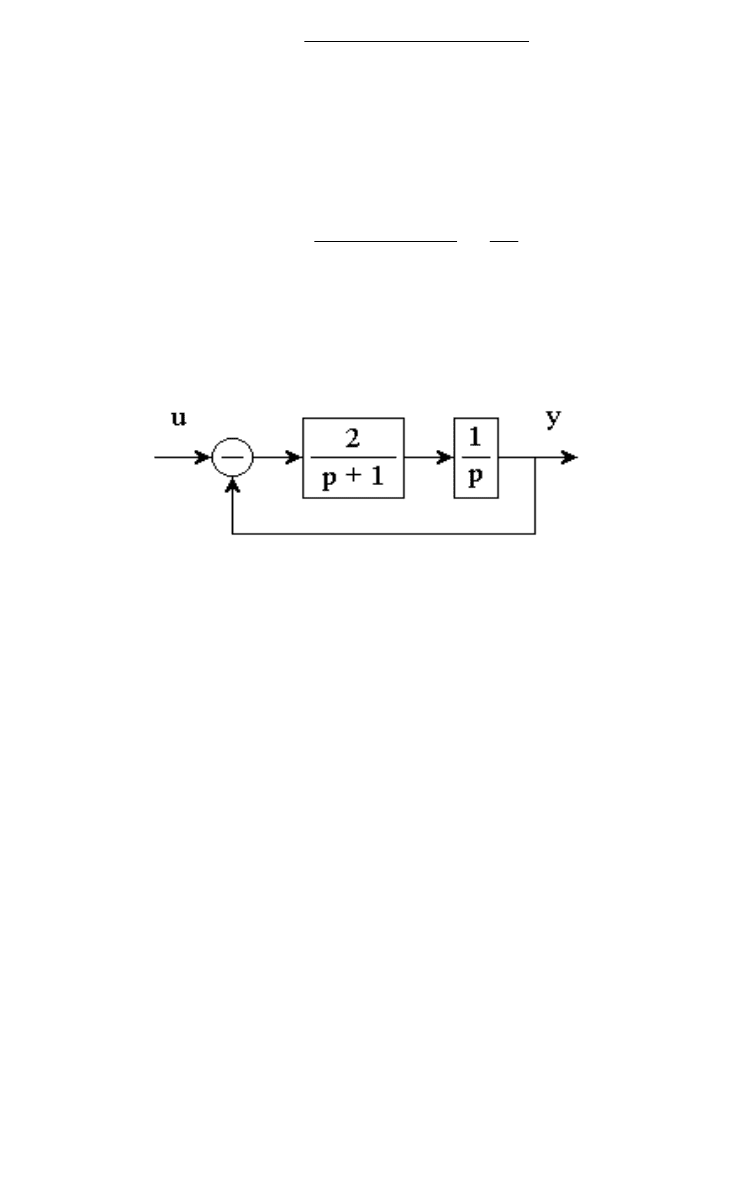
13.10. Дана структурная схема объекта:

Рис. 13.9

Проверить управляемость объекта.

13.11. Модель линейного объекта задана матрицами АВС следующего

вида:

0 1 1

1 0 0

1 1 0

 

 



 

 

;

0 1

1 1

1 0

 

 



 

 

;

 

1 0 1C 

Проверить управляемость объекта.

13.12. Даны уравнения состояний системы:

x Ax Bu

y Cx

 











 

0 1 1

, , 1 0 .

2 1 1

A B C

   

  

   

  

   

Проверить свойство управляемости объекта.

Пример 13.2. Модель объекта управления имеет вид

1 2

2 2 1

2 2 ,

x x

x x x u

y x







  











(14.1)

Требуется вычислить параметры закона управления на основе

матричной процедуры модального метода синтеза, обеспечивающего

выполнение следующих условий:

% 30%;



t c

Решение. Закон управления для объекта второго порядка имеет вид

1 1 2 2

u k x k x dv  

, (14.2)

где

1 2

, ,k k d

– неизвестные коэффициенты (параметры регулятора),

значение которых необходимо определить.

Подставив уравнение (14.2) в (14.1), получим систему уравнений,

которая описывает замкнутую систему:

1 2

2 2 2 1 1

2(1 ) (1 2 ) ,

x x

x k x k x dv

y x







    











Матрицы коэффициентов системы равны

1 2

0 1

;

1 2 2(1 )

k k

 



 

 

 

 



 

 

;

 

1 0C 

Определим характеристический полином системы

2 1

det( ) 2 (1 ) (1 2 ).pI A p p k k     

(14.3)

Неизвестные коэффициенты

можно определить из равенства

(14.3) полиному желаемого вида (

( )

С р

). На основе значения

найдем область допустимого расположения корней замкнутой системы.

Порядок системы равен 2, поэтому выбираем из области два корня,

например,

1,2

0.4 .p j 

Находим желаемый полином:

2 2

1 2

( ) ( )( ) (( 0.4) 1) 0.8 1.16

C p p p p p p p p        

(14.4)

Приравняв коэффициенты полиномов (14.3) и (14.4) при одинаковых

степенях р, имеем

0.6;k 

0.08k 

Из условия статики:

( )

lim

y t v

® 



, определим неизвестный коэффициент

1 1

( ) 0.43d CA B

 

 

Уравнение регулятора имеет вид

1 2

0.08 0.6 0.43u x x v  

Пример 13.3. Для объекта модель которого имеет вид

( )

3 1

W p

p p



 

рассчитать параметры регулятора , используя операторную процедуру

модального метода синтеза. Требования к качеству процессов в системе

следующие:

t 

с;

0%;



ст

 

Решение. Расчетная структурная схема замкнутой системы

Рис. 13.10

где

( ) /

W p k p

– составляющая регулятора, обеспечивающая

нулевую статическую ошибку;

1 0

( ) ( )/5

W p d p d 

– составляющая

регулятора, обеспечивающая динамические свойства; (

1 0

, ,k d d

) –

неизвестные коэффициенты.

Запишем характеристическое уравнение замкнутой системы

1 0

( ) ( 3 1 ) 5 0A p p p p d p d k      

или

3 2

1 0

( ) (3 ) ( 1) 5 0.A p p d p d p k      

Сформируем желаемое характеристическое уравнение 3 – го порядка,

выбрав распределение корней обеспечивающее заданное качество процессов





2.5;









Получим желаемое характеристическое уравнение

1 2 3

( ) ( )( )( ) 0С p p p p

  

    

или

3 2

( ) 7.5 18.5 15 0.C p p p p    

Приравнивая коэффициенты при соответствующих степенях оператора

р, получим расчетные соотношения

3 7.5,d 

1 18.5,d  

5 15.k 

Отсюда находим параметры регулятора

4.5;d 

19.5;d 

3.k 

13.13. Заданы требования к переходным процессам в системе в целом:

3 , 1.5.

t c

 

Записать желаемое характеристическое уравнение третьего порядка.

13.14. Заданы требования к переходным процессам в системе в целом:

5 , 20%, n 4.

t c

  

Записать желаемое характеристическое уравнение.

13.15. Составить модель системы стабилизации второго порядка,

качество процессов в которой удовлетворяли следующим требованиям:

Δ 5%, t 6с, σ 15%, lim (v y) , v const.

ст ст

     

® 

13.16. Записать желаемый характеристический полином четвертого

порядка по заданным показателям качества процессов:

Δ 10%, t 3с, σ 30%.

ст п

  

13.17. Записать желаемый характеристический полином третьего

порядка по заданным показателям качества процессов:

Δ 0%, t 10с, σ 40%.

ст п

  

13.18. Для объекта, модель которого задана передаточной функцией

( ) 2/( 1),W p p 

заданы требования к переходным процессам в системе в целом:

1 , 0%.t c

 

Рассчитать параметры регулятора модальным методом синтеза.

13.19. Для объекта, модель которого описывается передаточной

функцией

3 2

( ) 2/( 4 1),W p p p p   

Заданы требования к переходным процессам в системе в целом:

1 , 30%.t c

 

Найти параметры регулятора модальным методом

синтеза.

13.20. Модель объекта управления имеет вид

1 1 2

2 1 2

2 ,

x x x u

y x

  





  











Заданы требования к переходным процессам в системе в целом:

3 , 30%.t c

 

Рассчитать параметр регулятора модальным методом

синтеза.

13.21 Модель объекта управления имеет вид:

1 2

2 3

3 1 2 3

4 2 ,

x x

x x x x u

y x













   









Заданы требования к переходным процессам в системе в целом:

3 , 0%.

t c

 

Вычислить параметры регулятора модальным методом

синтеза.

13.22. Модель объекта управления имеет вид:

1 1 2

2 1 2

1 2

x x x u

x x x

y x x

  





 





 





Рассчитать параметры регулятора модальным методом синтеза. Обеспечить

требования:

t 

с,

30%.



13.23. Задан объект, поведение которого описывается передаточной

функцией вида

( ) [2(3 1)]/[(5 1)( 2)].W p p p p   

Рассчитать параметры

регулятора модальным методом так, чтобы качество переходных процессов в

замкнутой системе соответствовало следующим оценкам:

t 

с,

30%, 2% от .

ст

  

13.24. Модель объекта описывается передаточной функцией вида

( ) 2/[(3 1)(0,5 1)].W p p p  

Рассчитать параметры регулятора модальным методом синтеза по

требованиям к качеству переходных процессов:

t 

с,

0 Δ 2 от

ст

σ %, % v. 

13.25. Модель объекта заданна системой уравнений

1 1 2

2 1 2

1 2

x x x u

x x x

y x x

  





 





 





Рассчитать параметры регулятора модальным методом синтеза по

требованиям к качеству переходных процессов:

3 , 30%, 0% от .

п ст

t c v

   

13.26. Для объекта, поведение которого описывается передаточной

функцией вида

( ) [5(2 1)]/( 3 1),W p p p p   

рассчитать параметры

регулятора модальным методом по требованиям к качеству переходных

процессов:

5 , 0%, 2% от .

п ст

t c v

   

13.27. Задана модель объекта и требования к переходным процессам в

системе:

2y y u, 



Δ 0%, t 1с, σ 0%.

ст

  

Требуется определить

параметры регулятора модальным методом синтеза, изобразить структурную

схему системы.

13.28. Передаточная функция объекта управления имеет вид:

( ) 10/(4 0.4 1).W p p p  

Используя модальный метод синтеза

рассчитать параметры регулятора, который обеспечивает выполнение

следующих требований:

( ) 0, 30%, 1 .

t t с

    

13.29. Используя модальный метод синтеза рассчитать параметры

регулятора, обеспечивающего выполнение в замкнутой системе следующих

требований:

( ) 0, 30%, 1

t t

    

с. Модель объекта управления

имеет следующий вид:

1 2

2 1 2

2 10 ,

x x

x x x u

y x







  











13.30. Вычислить параметры закона управления на основе модального

метода синтеза. Необходимо обеспечить выполнение следующих условий:

30%; 10 ; 0;

п ст

t с

   

при

 

5;5 .f  

Модель объекта управления

имеет вид:

1 2

2 1 2

2 2 ,

x x

x x x u f

y x







   











13.31. Заданы модель объекта

1 2

2 1 2

0.25 0.1 0.025 ,

x x

x x x u

y x







  









