Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

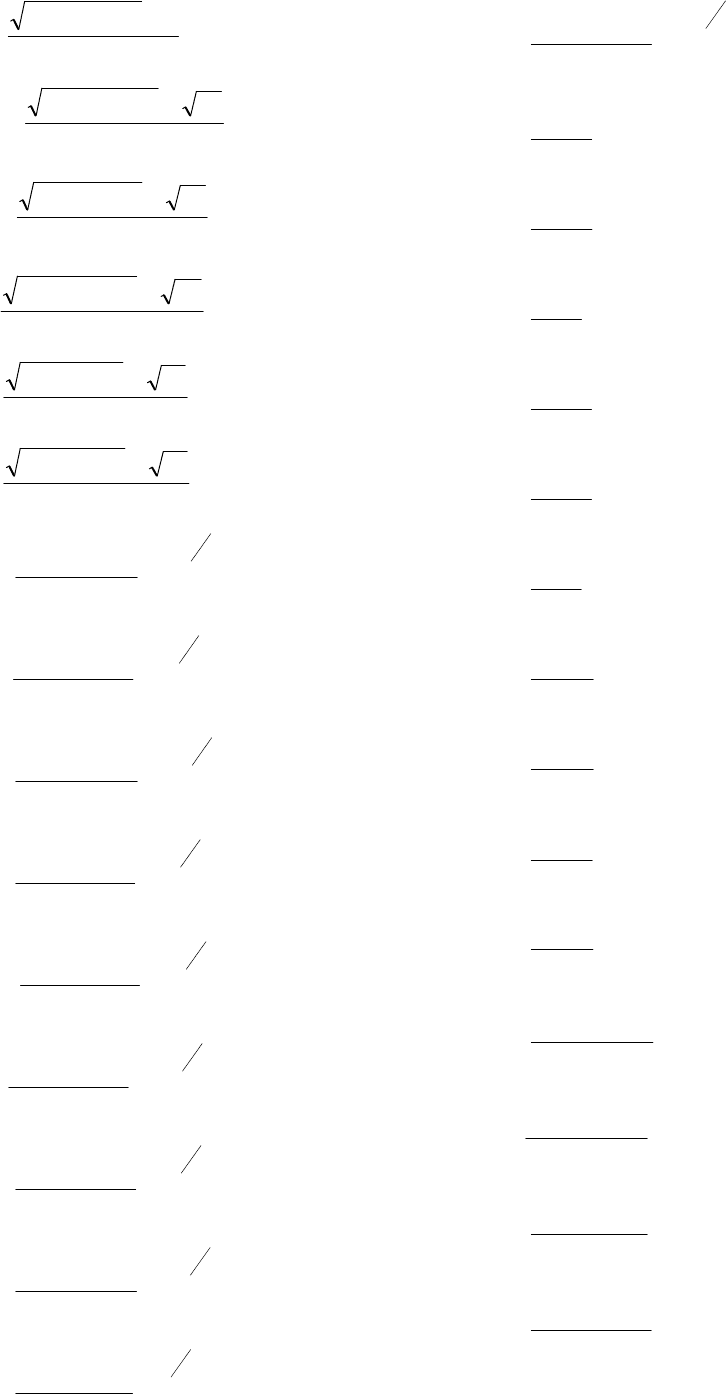
81
175.
;
1
2839
lim
2
1
+
−−−
−→
x
xx
x
176.
;
3
53164
lim
2
3
+
−−−
−→
x
xx
x
177.
;
2
33583
lim
2
2
−
−++
→
x
xx
x
178.
2
26436
lim
2
2
−
−−+
→
x
xx
x
179.
;
2
10433
lim
2
2
−
−+
→
x
x-x
x
180.
;
2
10454
lim
2
2
−
−+
→
x
x-x
x
181.
;
16
722
lim
)75(
)34(
2
2
−
−−
∞→
−−
−−
x
x
x
xx
xx
182.
;
936
386
lim
)47(
)73(
2
2
−−
−
∞→
++
−+
x
x
x
xx
xx
183.
;
695
764
lim
)19(
)74(
2
2
+−
+−
∞→
−+
−+
x
x
x
xx
xx
184.
;
96
968
lim
)37(
)35(
2
2
−
−
∞→
+−
−+
x
x
x
xx
xx
185.
;
689
86
lim
)1(
)66(
2
2
−
+
∞→
−+
−−
x
x
x
xx
xx
186.
;
795
66
lim
)19(
)56(
2
2
−
−−
∞→
−−
+
x
x
x
xx
x
187.
;
57
734
lim
)89(
)33(
2
2
−−
−
∞→
−−
−−
x
x
x
xx
xx
188.
)45(
)58(
2
2
48
344
lim
−−
−−
∞→
++
++
x
x
x
xx
xx
189.
;
77
152
lim
)22(
)8(
2
2
+
+
∞→
−
++
x
x
x
x
xx
190.
;
72
567
lim
)87(
)94(
2
2
+
−−
∞→
−−
−+
x
x
x
xx
xx
191.
9
95
55
lim
+−
∞→
+
+
x
x
x
x
192.
46
25
35
lim
−−
∞→
−
+
x
x
x
x
193.
48
2
4
lim
−−
∞→
+
+
x
x
x
x
194.
26
86
36
lim
+
∞→
−
−
x
x
x
x
195.
48
35
95
lim
−
∞→
+
−
x
x
x
x
196.
87
7
1
lim
+
∞→
+
−
x
x
x
x
197.
32
14
74
lim
−
∞→
+
−
x
x
x
x
198.
92
97
67
lim
−−
∞→
+
+
x
x
x
x
199.
6
78
98
lim
−−
∞→
+
−
x
x
x
x
200.
67
46
26
lim
+−
∞→
−
−
x
x
x
x
201.
86
2
2
664
424
lim
−
∞→
+−
+−
x
x
xx
xx
202.
95
2
2
524
264
lim
+−
∞→
−+
+−
x
x
xx
xx
203.
28
2
2
165
195
lim
+−
∞→
−−
++
x
x
xx
xx
204.
17
2
2
77
397
lim
−−
∞→
+
++
x
x
xx
xx
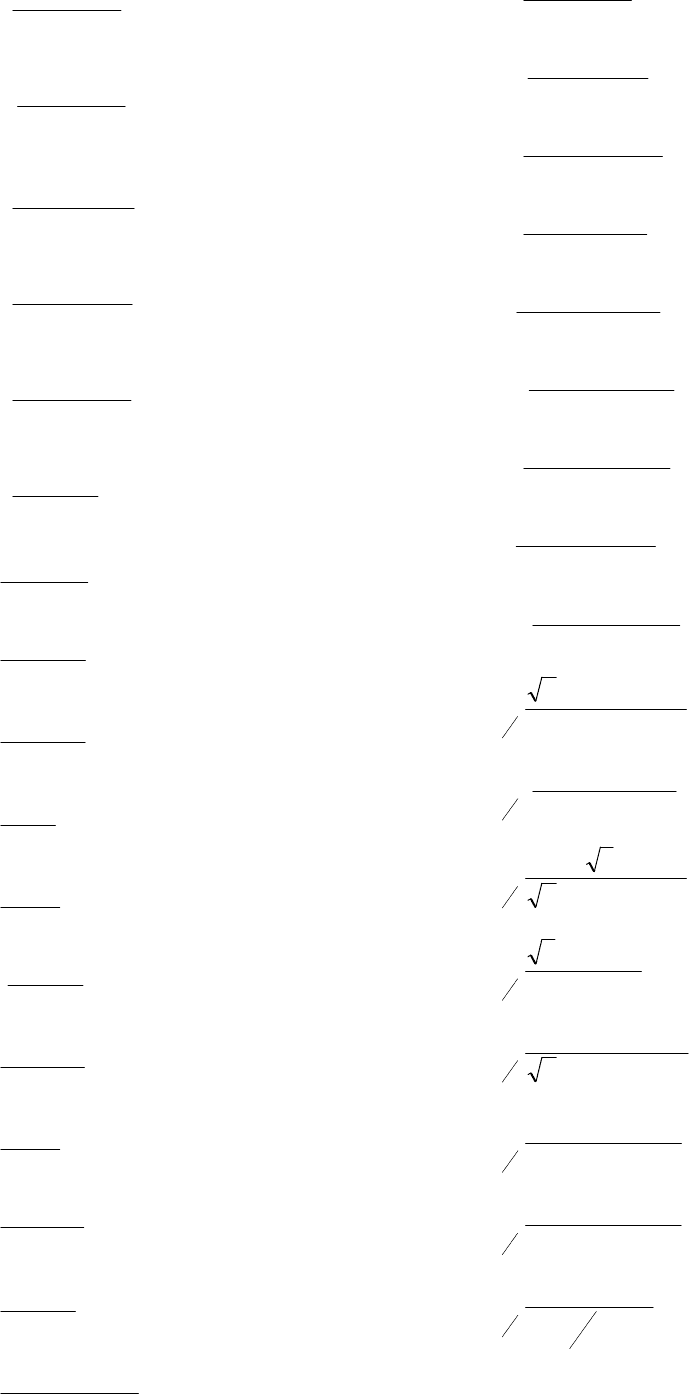
82
205.
98
2
2
43
23
lim
−−
∞→
−
++
x
x
x
xx
206.
48
2
2
87
5
lim
−
∞→
−+
+
x
x
xx
x
207.
86
246
796
lim
2
2
+
−+
−+
∞→
x
xx
xx
x
208.
98
2
2
77
397
lim
−−
∞→
+
+−
x
x
xx
xx
209.
54
2
2
363
193
lim
+
∞→
−−
−+
x
x
xx
xx
210.
49
2
2
8
68
lim
−−
∞→
−
x
x
x
xx
211.
x
x
x
5
arcsin
4arctg
lim
0→
212.
x
x
x
arctg8
9arcsin
lim
0→
213.
x
x
x
5tg
arcsin7
lim
0→
214.
x
x
x
7tg
sin2
lim
0→
215.
x
x
x
7
sin
2tg
lim
0→
216.
arctg9x
4sin
lim
0
x
x→
217.
x
x
x
3arctg
arcsin8
lim
0→
218.
x
x
x
4
sin
tg9
lim
0→
219.
x
x
x
9arcsin
2
lim
0
−
→
220.
;
3tg
arctg6
lim
0
x
x
x→
221.
;
16
)246arctg(
lim
2
4
−
−
→
x
x
x
222.
;
4
3
)99sin(
lim
2
1
−
+
−
→
x
x
x
x
223.
;
7
4
3
)7sin(7
lim
2
1
−
−
+
−→
x
x
x
x
224.
;
4
4
8
)44sin(
lim
2
1
+
+
−
−
→
x
x
x
x
225.
;
28
3
)4arcsin(
lim
2
4
−
+
−
→
x
x
x
x
226.
;
18
21
9
)155arcsin(
lim
2
3
−
−
−
→
x
x
x
x
227.
;
32
20
7
)82arctg(
lim
2
4
−
+
+
−→
x
x
x
x
228.
;
8
34
9
)205arcsin(
lim
2
4
−
−
−
→
x
x
x
x
229.
;
4
6
2
)9sin(9
lim
2
1
−
+
−
−
→
x
x
x
x
230.
;
6
11
7
)63sin(
lim
2
2
+
+
−
−
→
x
x
x
x
231.
(
)
;
)4 (arcsin
sincos2
lim
4
x/π
xx
x
−
−
→
π
232.
;
)4 arctg(
2cos
lim
4
x/π
x
x
−
→
π
233.
( )
;
sincos2
sin82
lim
4
xx
x
x
−
−
→
π
234.
;
2cos
2cos8
lim
4
x
x
x
−
→
π
235.
;
)sin(cos2
1ctg
lim
4
xx
x
x
−
−
→
π
236.
;
tg1
2sincos2
lim
2
4
x
xx
x
−
−
→
π
237.
xx
x
x
2sincos2
tg1
lim
2
4
−
−
→
π
238.
)
4
tg(
)4/cos(
lim
4
x
x
x
−
+
→
π
π
π
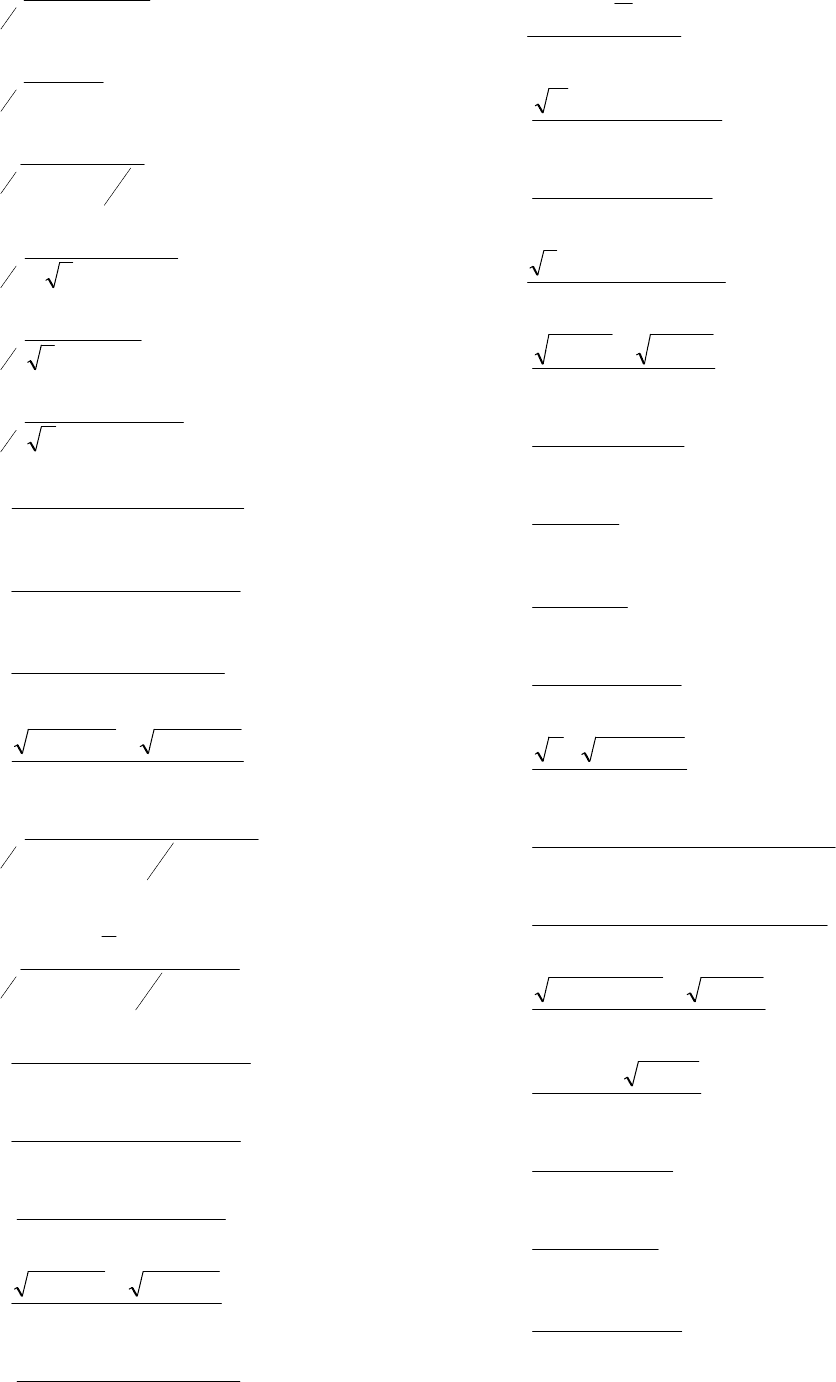
83
239.
1ctg
)4/(ctg
lim
4
−
+
→
x
x
x
π
π
240.
x
x
x
tg1
4/
lim
4
−
−
→
π
π
241.
)
4
cos(x
)4/sin(
lim
4
π
π
π
+
−
→
x
x
242.
4
lim
π
→x
2cos8
)4/arcsin(
−
−
x
x
π
243.
4
lim
π
→x
2cos8
)4/(tg
−
−
x
x
π
244.
4
lim
π
→x
)sin(cos2
)4/(arctg
xx
x
−
−
π
245.
1)arctg(x
)35cos()13cos(
lim
1
−
−
−
−
→
xx
x
246.
)1arctg(x
)89sin()78sin(
lim
1
−
−
−
−
→
xx
x
247.
)2arcsin(
)27(tg)12(tg
lim
2
−
−
−
−
→
x
xx
x
248.
π
π
−
−−+
→
x
xx
x
8sin18sin1
lim
249.
4
lim
π
→x
4
)8cos()4/34(tg
π
π
−
−
−
x
xx
250.
4
)6sin(
4
3
4
lim
4
π
π
π
−
+
−
→
x
xxtg
x
251.
;
)52cos()52(cos
lim
0
x
xx
x
−
−
+
→
252.
x
xx
x
)63sin()63sin(
lim
0
−
−
+
→
253.
0
lim
→x
;
)41(tg)41(tg
x
xx
−
−
+
254.
x
xx
x
sin1sin1
lim
0
−−+
→
255.
0
lim
→x
;
)8cos()24/(tg
x
xx
−
+
π
256.
x
x
x
+−
→
6
sin21
lim
0
π
257.
0
lim
→x
;
)63/(2sin 3
x
x- +
π
258.
0
lim
→x
;
)23/( 2cos-1
x
x
+
π
259.
;
)46/(2cos-3
lim
0
x
x
x
+
→
π
260.
0
lim
→x
;
tg1tg1
x
xx
−−+
261.
0
lim
→x
;
)54/(tg-1
x
x
+
π
262.
0
lim
→x
;
cos5-1
2
x
x
263.
0
lim
→x
;
4cos-1
2
3
x
x
264.
0
lim
→x
;
3cos7 cos
2
x
xx
−
265.
0
lim
→x
;
cos41-2
2
x
x+
266.
0
lim
→x
;
sin1)52sin(1-)10sin(1
2
x
xx
+
+
+
267.
0
lim
→x
;
4tg)74(tg2)144(tg
2
x
xx
+
+
−
+
268.
0
lim
→x
;
4cos3sin81
2
x
xxx −+
269.
0
lim
→x
2
3cos9cos1
x
xx−
270.
0
lim
→x
3
sin77sin
x
xx
−
271.
0
lim
→x
3
6sin6tg
x
xx
−
272.
0
lim
→x
4
22
9sin9tg
x
xx −
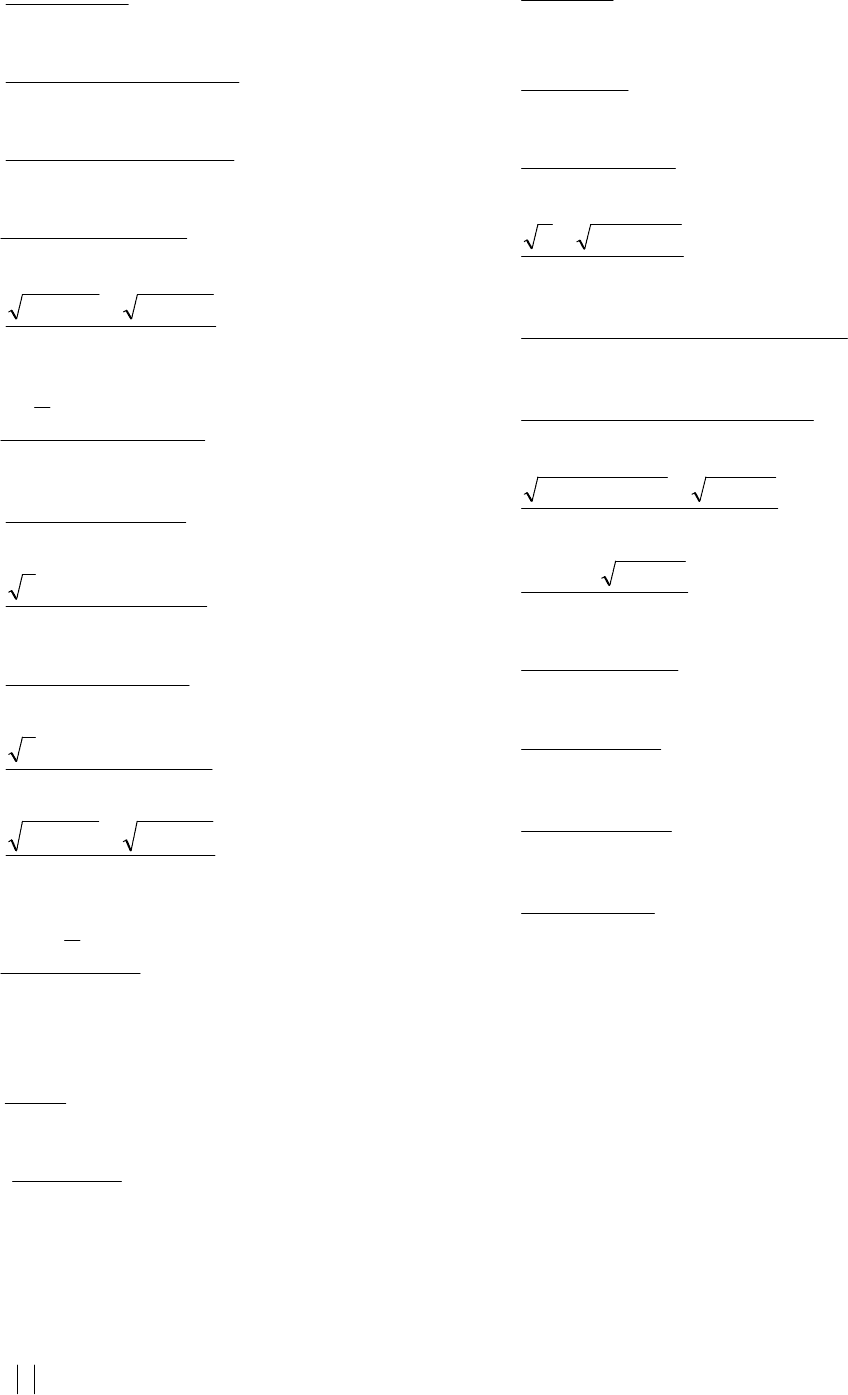
84
273.
0
lim
→x
5
33
sintg
x
xx −
274.
0
lim
→x
x
xx
sin
)81( cos)81cos(
−
−
+
275.
0
lim
→x
x
xx
arcsin
)93sin()93sin(
−
−
+
276.
tgx
x)tg(1x)tg(1
lim
0
−
−
+
→x
277.
0
lim
→x
x
xx
sin
sin1sin1 −−+
278.
x
x
tg
cos(6x)5x
4
π
tg
lim
0
−
+
→
279.
0
lim
→x
x
x
sin
)56/sin(21
+
−
π
280.
0
lim
→x
x
x
arcsin
)23/sin(23 +−
π
281.
0
lim
→x
x
x
sin
)63/cos(21
+
−
π
282.
0
lim
→x
x
x
sin
)46/cos(23 +−
π
283.
0
lim
→x
;
tg
8tg18tg1
x
xx −−+
284.
arctgx
8x
4
π
tg1
lim
0
+−
→x
285.
0
lim
→x
;
arcsin
9cos1
x
x
x
−
286.
0
lim
→x
;
sin
9
3
cos1
x
x
x−
287.
0
lim
→x
;
tg
3соs9cos
xx
x x
−
288.
0
lim
→x
;
arctg
8cos12
xx
x+−
289.
0
lim
→x
;
tg
3sin)43(sin2)83(sin
xx
x x
+
+
−
+
290.
0
lim
→x
;
arctg
1tg)71tg(2)141tg(
xx
x x
+
+
−
+
291.
0
lim
→x
;
sin
7cos4sin81
x
x
x x x −+
292.
0
lim
→x
;
sin
2coscos1
x
x
x x−
293.
0
lim
→x
;
sin33sin
3
x
x x -
294.
0
lim
→x
;
2sin2 tg
3
x
x x -
295.
0
lim
→x
;
6sin6tg
4
22
x
xx −
296.
0
lim
→x
.
sin
sintg
5
33
x
x x −
Исследовать непрерывность следующих функций:
297.
5
3
23
+
−
=
x
x
y
298.
2
6
)12(sin
2
−
+
=
x
x
x-
y
299.
>
≤+
=
1если
1если 1
2
- х, х
- х, x
y
300.
[
]
[ ]
∉
∈
=
11 если ,
11 если ,
2
, - х х
, - х x
y
301.
>+
≤≤++
<+
=
3если,24
31если132
1если53
23
хх-
х - , хх
- х , x
y
302.
≥−
<≤−
<+
=
4если42
43если7
3если12
2
х,
x x, х
х,
y
x
x
85
303.
>−−+
≤<
≤
=
.3если14
3
3
1
еслиlog
31если23
3
2
3
х, xx
x x,
х, х-
y
304.
>+
≤≤
<
−
+
=
2если,1
20если2
0если
1
1
2
x x
x x,
х,
x
x
y
305.
≥
<<
≤
=
1 xесли,
10если
0еслиcos
x
x , e
x x,
y
x
306.
>
≤≤+
<−
=
2если,
22если42
2если37
2
x x
x -, x
- x , x
y
4.2 Производная
Пусть функция
)
(
x
f
y
=
определена на интервале
),( ba
. Дадим
аргументу
),( bax
∈
приращение
0
≠
∆
x
такое, что
),(
baxx
∈
∆
+
, тогда
функция y получит соответствующее приращение
)()(
xfxxfy
−
∆
+
=
∆
.
Если существует конечный предел
x
xfxxf
x
y
x
∆
−
∆
+
=
∆
∆
→∆
)()(
limlim
0
,
то он называется производной функции
)
(
x
f
в точке
x
и обозначается
x
xfxxf
x
y
xf
x
∆
−
∆
+
=
∆
∆
=
′
→∆
)()(
limlim)(
0
.
Пример 1.
Найти, исходя из определения, производную функции
xy =
(
0
≥
x
).
Зададим приращение
x
∆
, такое, что
0
≥
∆
+
xx
.
Тогда
xxxy −∆+=∆
;
Поэтому
x
xxx
x
y
∆
−∆+
=
∆
∆
;
Переходим к пределу при
0
→
∆
x
и получаем
xxxxx
x
x
xxx
x
y
xy
xxx
2
1
)(
limlimlim)(
000
=
+∆+∆
∆
=
∆
−∆+
=
∆
∆
=
′
→∆→∆→∆
;
86
т.е.
x
x
2
1
)(
=
′
.
Основные правила дифференцирования.
Пусть
)(xf
,
)(x
ϕ
- дифференцируемые функции, а
с
- некоторая
постоянная, тогда справедливы следующие правила дифференцирования:
1.
0
=
′
c
;
2.
ϕ
ϕ
′
±
′
=
′
±
ff )(
;
3.
fccf
′
=
′
)(
;
4.
ϕ
ϕ
ϕ
′
⋅
+
⋅
′
=
′
⋅
fff )(
;
5.
2
ϕ
ϕϕ
ϕ
′
⋅−⋅
′
=
′
fff
;
0
≠
ϕ
.
6.
Производная сложной функции.
Если функции
)(ufy
=
и
)(xu
ϕ
=
имеют конечные производные, то
xux
ufy
′
⋅
′
=
′
Таблица производных основных элементарных функций:
1.
umuu
mm
′
=
′
−1
)(
; 11. uuec
u
uctg
′
⋅−=−=
′
2
2
cos
sin
1
) (
;
2.
(
)
u
u
u
′
=
′
2
1
; 12. u
u
′
−
=
′
2
1
1
)u(arcsin
;
3.
u
uu
′
−=
′
2
11
; 13.
u
u
u
′
⋅
−
−=
′
2
1
1
) (arccos
;
4.
uee
uu
′
=
′
)(
; 14.
u
u
uarctg
′
⋅
+
=
′
2
1
1
) (
;
5.
auaa
uu
ln)(
′
=
′
; 15.
u
u
uarcctg
′
⋅
+
−=
′
2
1
1
) (
;
6.
u
u
u
′
=
′
1
)(ln
; 16.
uchu
ee
ush
uu
′
⋅=
′
−
=
′
−
2
) (
;
7.
u
a
u
u
a
′
=
′
ln
1
)(log
; 17.
ushu
ee
uch
uu
′
⋅=
′
+
=
′
−
2
) (
;
8.
uuu
′
⋅
=
′
cos)(sin
; 18.
u
uch
chu
shu
uth
′
⋅=
′
=
′
2
1
) (
;
9.
uuu
′
⋅
−
=
′
sin)(cos
;
19.
u
ush
shu
chu
ucth
′
⋅=
′
=
′
2
1
) (
.

87
Пример 2.
Найти производную функции
x
x
x
arctgxxy
sin
cos
cos
2
+
+=
.
)sin(cos
1
1
2
)sin(cos
cossincossicossin
1
2
)sin(cos
)sin(coscos)sin(cos)(cos
)()(
22
2
2
22
2
2
2
22
xxx
x
arctgxx
xx
xxxxnxx
x
x
arctgxx
xx
xxxxxx
arctgxxarctgxxy
+
−
+
+=
=
+
−+−−
+
+
+=
=
+
′
+
−
+
′
+
′
+
′
=
′
.
Пример 3.
Найти производную
)32(ln
+
=
xtgy
.
Берем производную от
y
как сложной функции
(
)
))((ln xvuy
=
, где
tgv
u
=
,
32
+
=
xv
.
x
vu
xvu
y
′
⋅
′
⋅=
′
υ
))((
1
, где
)32())((
+
=
xtgxvu
,
v
u
2
cos
1
=
′
υ
;
2=
′
x
v
.
Итак,
2
)32(cos
1
)32(
1
2
⋅
+
⋅
+
=
′
x
xtg
y
.
Логарифмическое дифференцирование
В некоторых случаях для нахождения производной заданную
функцию логарифмируют, а затем полученное выражение
дифференцируют. Такая операция называется логарифмическим
дифференцированием.
Пример 4.
Найти производную функции
tgx
xy
)(sin
=
Прологарифмировав заданную функцию, получим
x
tgx
y
sin
ln
ln
=
.
Находим производные от сложных функций в левой и правой частях
равенства

88
1
cos
)ln(sin
cos
sin
1
)ln(sin
cos
1
22
+=⋅+=
′
x
x
x
x
tgxx
xy
y
.
Отсюда выражаем производную
+=
+⋅=
′
1
cos
)ln(sin
)(sin1
cos
)ln(sin
22
x
x
x
x
x
yy
tgx
.
Производная неявной функции.
Для нахождения производной от
y
по
x
неявно заданной функции
0),(
=
yxF
, нужно продифференцировать это уравнение по
x
,
рассматривая
y
как функцию
x
. Затем полученное уравнение
разрешается относительно
y
′
.
Пример 5.
Найти производную функции
y
, заданную уравнением
05
55
=−+ xyyõ
.
Дифференцируем по
x
равенство
05
55
=−+ xyyõ
. Из полученного
соотношения
0)1(555
44
=
′
⋅+⋅−
′
⋅+ yxyyyx
следует, что
44
xyyxyy −=
′
⋅−
′
⋅
или
xy
xy
y
−
−
=
′
4
4
.
Производная функции, заданной параметрически
Если зависимость между
x
и функцией
y
задана параметрически в
виде двух уравнений
=
=
),(
),(
tyy
txx
где
t
-вспомогательная переменная, называемая параметром, то
производные
x
y
′
и
x
y
′
′
функции определяются по правилу
t
t
x
x
y
y
′
′
=
′
и
( )
3
t
tttt
x
x
xyyx
y
′
′
′
′
−
′
′
′
=
′′
.
Пример 6.
Найти
dx
dy
y
=
′
, если
t
a
x
cos
=
,
tby sin
=
.
Имеем
ctgt
b
a
tb
ta
dt
dx
dt
dy
dx
dy
−=
−
+
==
sin
cos
.
Производная обратной функции.
Пусть функция
)(xfy
=
строго монотонна в некоторой окрестности
точки
0
x
и дифференцируема, в точке
0
x
причем её производная
)(
0
xf
′

89
отлична от нуля. Тогда обратная функция )( ygx
=
определена в
некоторой окрестности соответствующей точки )(
00
xfy
=
,
дифференцируема в этой точке и имеет в этой точке производную,
равную
)(
1
)(
0
xf
yg
′
=
′
.
Пример 7.
Найти производную
x
a
.
Показательная функция
x
ay =
, является обратной для
логарифмической функции
yx
a
log=
. Для ее производной справедлива
формула
aa
e
a
e
y
ey
a
x
a
x
aa
y
a
x
ln
logloglog
1
)(log
1
)(
1
====
′
=
′
.
Итак,
aaa
xx
ln)( =
′
.
Дифференциал функции.
Пусть функция
)
(
x
f
y
=
дифференцируема в точке
x
, тогда ее
приращение можно записать в виде
xxxxfy
∆
∆
+
∆
′
=
∆
)()(
α
, где 0)(lim
0
=
∆
→∆
x
x
α
.
Главная, линейная относительно
x
∆
часть xxf
∆
′
)( приращения
функции называется дифференциалом функции и обозначается
dy
:
xxfdy
∆
′
=
)(
.
При
x
x
f
=
)
(
, получим
x
x
x
dx
∆
=
∆
′
=
, поэтому дифференциал
функции
)
(
x
f
y
=
примет вид
dxxfdy )(
′
=
.
Основные свойства дифференциала.
1
.
,
0
=
dC
где
C
= const,
2
.
Cdu
Cu
d
=
)
(
3.
dv
du
v
u
d
±
=
±
)
(
,
4
.
vdu
udv
uv
d
+
=
)
(
,
5
.
)0( ,
2
≠
−
=
v
v
udvvdu
v
u
d
6
.
duufudf )()(
′
=
.

90
Пример 8.
Найти дифференциал функции y=ln(cosx).
tgxdxdx
x
x
dxxdy
−=−=
′
=
cos
sin
))(ln(cos
.
Задачи для самостоятельного решения.
1. Используя определение производной, найти производные функции
в точке x = x
0
.
1. f(x) = 3x + 1 2. f(x) = 7x + 2
3. f(
x) = 4x
2
+ 1 4. f(x) = 2x
2
+ x – 3
5. f(
x) = x
3
+ 2x – 4 6. f(x) = 2 x
2
– 3x + 4
7. f(
x) =
x
8. f(
x) = 32 +x
9. f(
x) =
2
1
x
10. f(x) =
4
1
2
+
x
11. f(
x) =
x
1
12. f(x) =
1
1
−
x
13. f(
x) = sin 2x
14. f(x) =
2
cos
x
15. f(
x) = )x( 23sin
−
16. f(x) =
+
1
3
cos
x
17. f(
x) =
x
2
18. f(
x) = 10
x
19. f(x)= log
2
x 20. f(x)=lgx
2. Найти производные у′ функций:
21. у = x
3
– 3x
2
+ 2x – 1
22. у =
4
4
x
+ x
3
+ 2x – 3
23. у =
2
473
25
+− xx
24. у = 1
41
3
2
3
+−+−
x
x
xx
25. у =
4
5
3
11
x
x
x
x
−++
26. у =
x
xxx
52
3
23 −+
27. у =
7
3
3
532
x
x
x
−+
28. у =
4
32
5
4
3
xxx
+−
29. у =
2
7 23
252
x
xxx
++−
30. у =
2
23
1
2
)(x
xxx
+
++
