Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

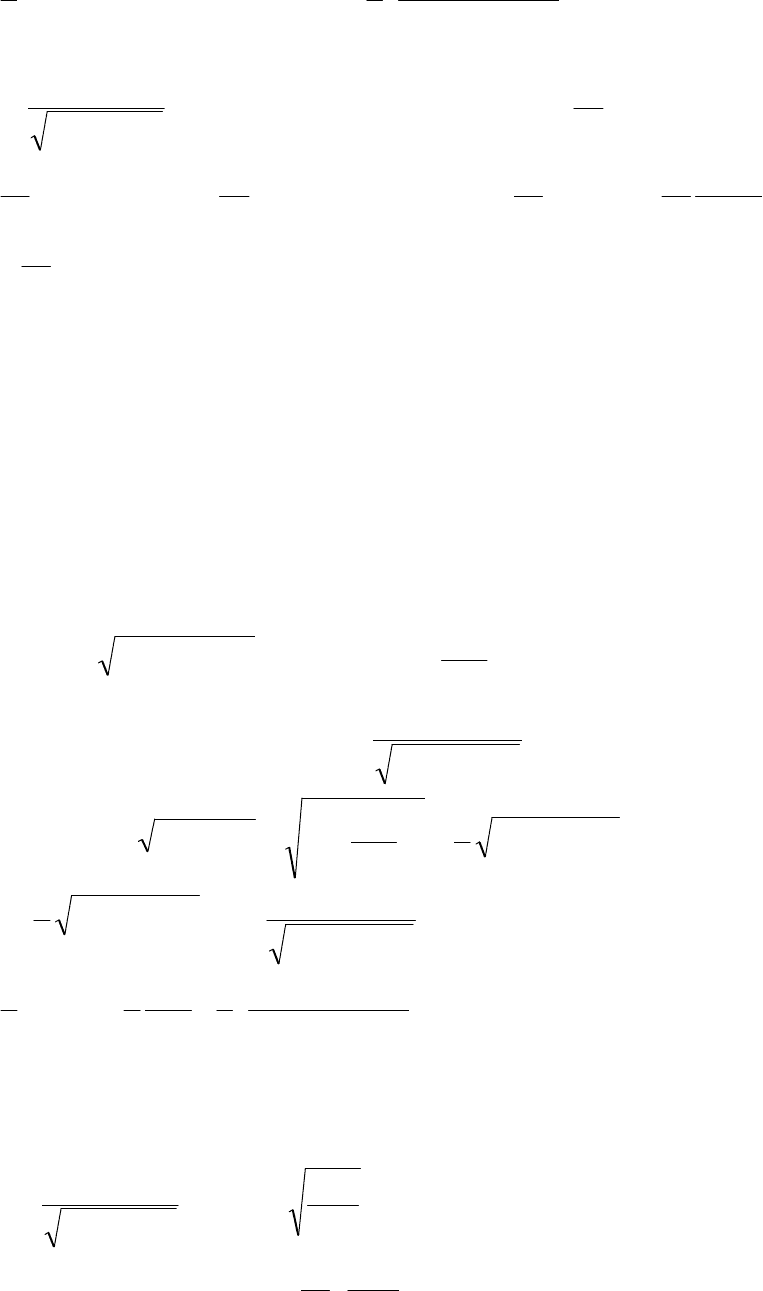
111
= )16(sin1)sin(6
6
1
7/2
+⋅+
∫
xdx = C
x
+
+
⋅
7
/
9
1)sin(6
6
1
7/9
.
6.
dx
x
x
4
73
2
4)(7 −
∫
= dxxx
4/732
4)(7
−
−⋅
∫
=
=
∫
3
3
2
x
dxx =
=
)421
3
(4)(7
21
1
3
4/73
−⋅−
−
∫
x
dx =
[
]
47
3
−= xt =
∫
−
dtt
4/7
21
1
=
C
t
+
−
−
4
/
3
21
1
4/3
=
=
Cx +−−
−
4/33
)47(
63
4
.
Вместо внесения под знак дифференциала можно применять метод замены
переменной, который также называют методом подстановки:
=)( dxxu
∫
=
′
=
=
−
)(
)(
)(
1
xt
dttdx
tx
ϕ
ϕ
ϕ
.)())((= dtttu
'
ϕϕ
∫
Используя замену переменной задачи 5 и 6 будут решаться так:
5a.
dxxx
7
2
1)sin(6cos +
∫
=
( )
−−
=
−
=
+=
dt
t
dx
t
x
xt
2
136
1
6
1
arcsin
1sin6
=
Т.к.
( )
2
2
2
136
6
1
6
1
1sin1cos −−=
−
−=−= t
t
xx , то
=
( )
( )
dt
t
tt
2
7/2
2
136
1
)(136
6
1
−−
−−
∫
=
=
7
/
9
6
1
6
1
7/9
7/2
t
dtt =
∫
= C
x
+
+
⋅
7
/
9
1)sin(6
6
1
7/9
.
6a.
dx
x
x
4
73
2
4)(7 −
∫
=
+
=
+
=
−=
−
dt
t
dx
t
x
xt
3/2
3
3
7
4
21
1
7
4
47
=

112
= dt
t
t
t
3/2
4/7
3/2
7
4
21
1
7
4
−
−
+
⋅
+
∫
=
∫
−
dtt
4/7
21
1
=
C
t
+
−
−
4
/
3
21
1
4/3
=
=
Cx +−−
−
4/33
)47(
63
4
.
Метод интегрирования по частям ( duvuvdvu
∫∫
−= ) − еще один
важный метод интегрирования, который продемонстрируем на следующем
примере
:
7.
dxex
x
−
∫
=
−==
==
−−
xx
evdxedv
dxduxu
;
;
=
dxexe
xx
∫
−−
+−
=
C
e
xe
xx
+−−
−−
.
Интегрирование по частям применяется для следующих, часто
встречающихся случаев ( )(xP
n
− многочлен степени
n
):
∫
kxdxxP
n
sin)( ,
∫
kxdxxP
n
cos)( ,
∫
dxexP
kx
n
)( (здесь через
u
следует обозначить )(xP
n
);
∫
xdxxP
k
n
ln)( ,
∫
kxdxxP
n
arcsin)( ,
∫
kxdxxP
n
arccos)( ,
∫
arctgkxdxxP
n
)( ,
∫
arcctgkxdxxP
n
)( (в этих случаях через
dv
следует обозначить dxxP
n
)( ).
Отметим, что по заданному дифференциалу
dv
, функция
v
определяется
неоднозначно (
∫
= dvv ), поэтому следует выбирать в качестве
v
наиболее
простую формулу.
Далее при нахождении неопределенного интеграла надо изучить методы
интегрирования некоторых классов функций. В примере 8 используется
правило интегрирования выражений вида
c
bx
ax
BAx
+
+
+
2
− в частности, надо
выделить полный квадрат, чтобы узнать какую замену переменной следует
сделать (аналогично интегрируются выражения вида
cbxax
BAx
++
+
2
):
8.
dx
x
x
x
15
8
6
2
+
+
+
∫
= dx
x
x
1)4(
6
2
−+
+
∫
=
=
−=
+
=
dtdx
tx
xt
4
4
=
∫
−
+
dt
t
t
1
2
2
=
=
∫ ∫
−
+
−
⋅ dt
t
dt
t
t
1
1
2
1
1
22
=
=
∫
2
2
t
tdt =
∫
+
−
+−⋅
−
1
1
ln)12
2
(
1
1
2
1
2
2
t
tt
d
t
=
=
C
t
t
t +
+
−
+−
1
1
ln1ln
2
1
2
= C
x
x
xx +
+
+
+++
5
3
ln158ln
2
1
2
.
В следуюшем примере применяем метод интегрирования выражений вида
cbxax
xP
n
++
2
)(
, где )(xP
n
- многочлен степени
1
,
≥
n
n
. Можно показать, что
интеграл от этой дроби можно представить в виде суммы двух слагаемых:
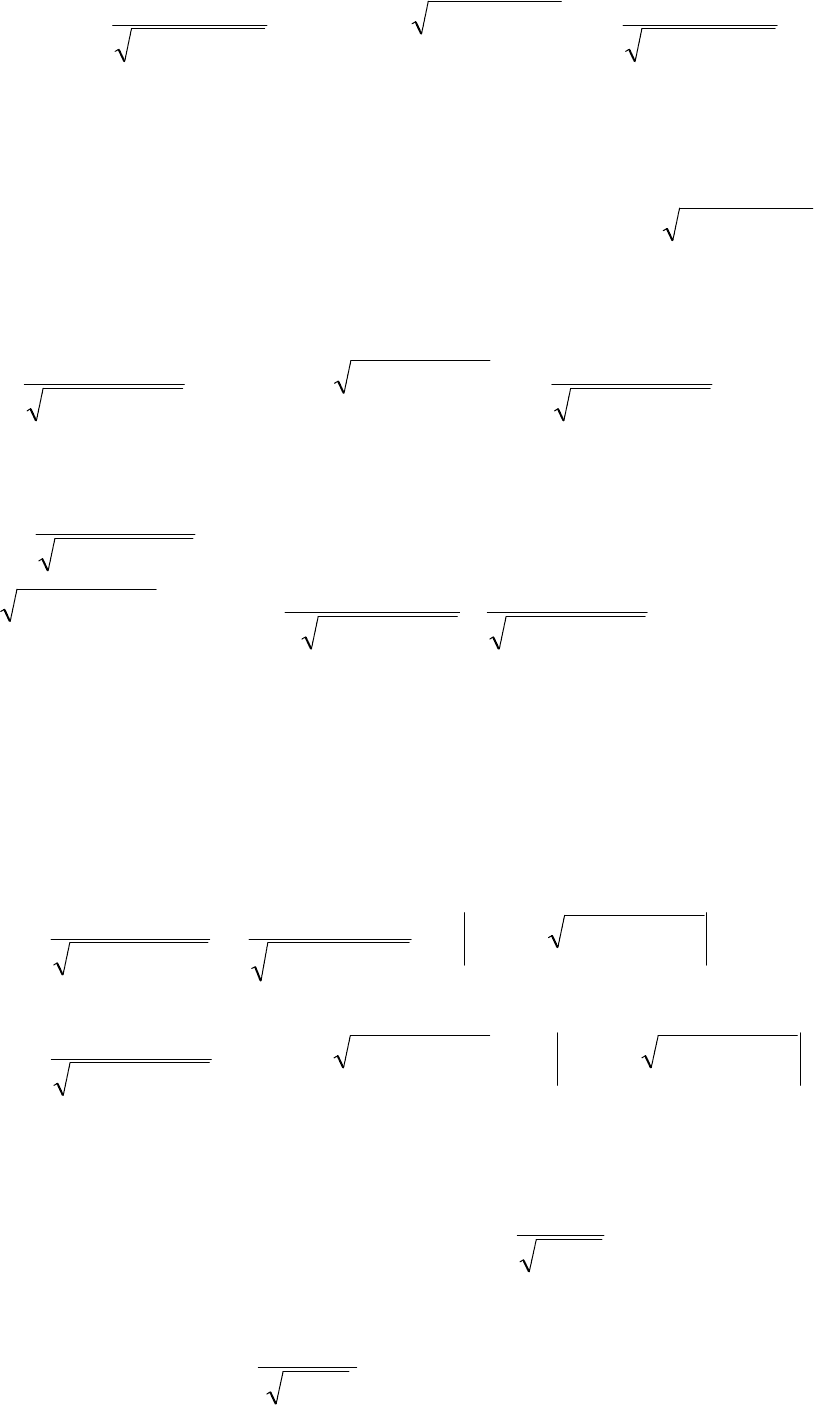
113
(1)
∫∫
++
+++=
++
−
cbxax
dx
cbxaxxQdx
cbxax
xP
n
n
2
2
1
2
)(
)(
α
,
где )(
1
xQ
n−
— многочлен с неопределенными коэффициентами степени
1
−
n
. Чтобы найти коэффициенты этого многочлена, а также постоянную
α
надо:
1. продифференцировать обе части равенства (1),
2. затем умножить обе части полученного равенства на
cbxax ++
2
(после чего получим равенство двух многочленов)
3. приравнять коэффициенты при одинаковых степенях переменной
x
4. решить полученную систему линейных уравнений.
9.
dx
x
x
xx
20
4
1872
2
2
+−
+−
∫
=
( )
∫
+−
++−+
20
4
204
2
2
x
x
dx
xxBAx
α
Сначала находим
α
,
,
B
A
. Для этого дифференцируем левую и правую
часть предыдущего равенства:
204
1872
2
2
+−
+−
xx
xx
=
20
4
20
4
2
42
)(204
22
2
+−
+
+−
−
+++−
x
x
x
x
x
BAxxxA
α
Отсюда получаем
18
7
2
2
+−
x
x
=
α
+−+++− )2)(()204(
2
xBAxxxA .
Теперь приравниваем коэффициенты при
012
,, xxx :
12:
2
=⇒+= AAAx
16247:
1
−=⇒+−=+−−=− BBBAAx
42222018:
0
−=⇒+=+−=
ααα
BAx
И, наконец, находим интеграл
∫
+− 204
2
xx
dx
=
2042ln
16)2(
)2(
2
2
+−+−=
+−
−
∫
xxx
x
xd
Следовательно,
dx
x
x
xx
20
4
1872
2
2
+−
+−
∫
=
( )
Cxxxxxx ++−+−−+−− 2042ln42041
22
.
Теперь можно показать применение интегрирования по частям на более
сложном (по сравнению с примером 7) примере:
10.
dxxx arccos4)(10 −
∫
=
−=−=
−
−
==
xxvdxxdv
x
dx
duxu
45,)410(
1
,arccos
2
2
=
=
∫
−
−
+⋅− dx
x
xx
xxx
2
2
2
1
45
arccos)45( =
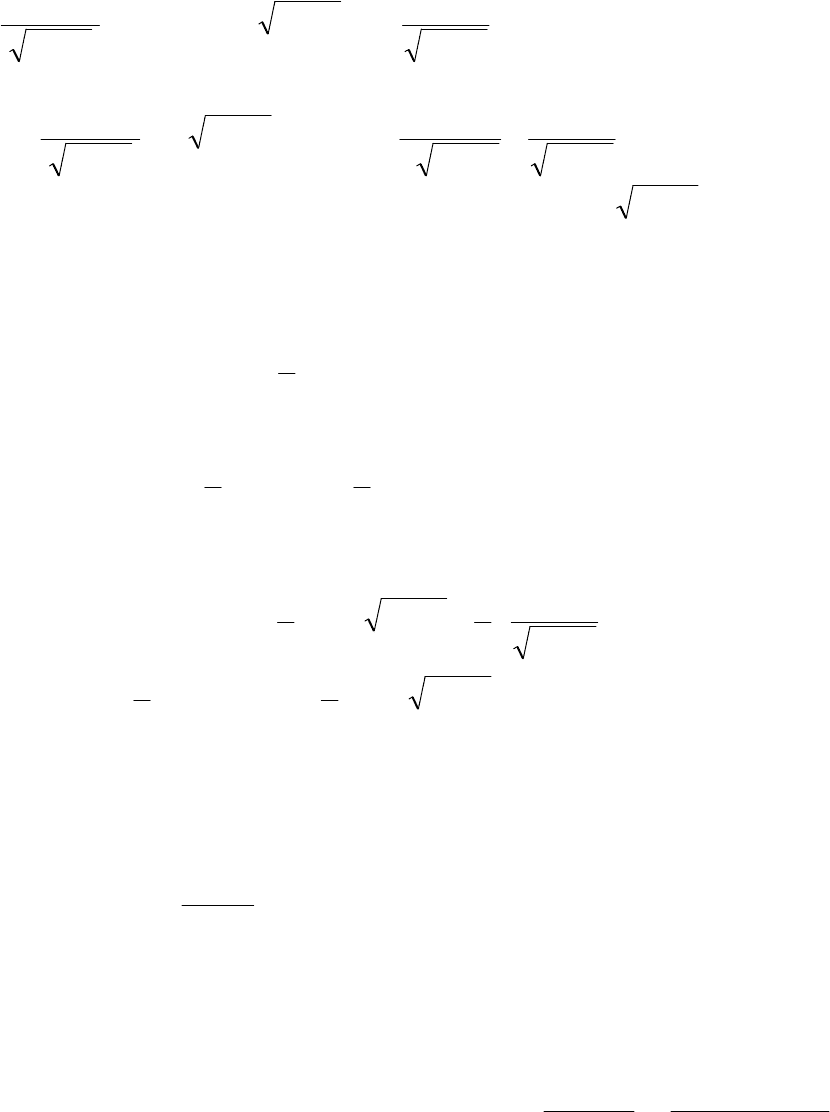
114
Получившийся интеграл находим так (см. предыдущий пример):
∫ ∫
−
+−+=
−
−
dx
x
xBAxdx
x
xx
2
2
2
2
1
1
1)(
1
45
α
Дифференцируем обе части этого равенства:
22
2
2
2
1
1
2
2
)(1
1
45
x
x
x
BAxxA
x
xx
−
+
−
−
++−=
−
−
α
Умножаем обе части полученного равенства на
2
1 x− :
α
++−−=− )()1(45
22
BAxxxAxx
Приравнивая коэффициенты при одинаковых степенях переменной
x
,
находим значения неизвестных величин
α
,
,
B
A
:
2
5
5:
2
−=⇒−−= AAAx
44:
1
=⇒−=− BBx
2
5
2
5
0:
0
=⇒+−=+=
ααα
Ax
Теперь продолжаем решать исходную задачу:
=
∫
−
+−+−+⋅− dx
x
xxxxx
2
22
1
1
2
5
1)4
2
5
(arccos)45( =
=
Cxxxxx +−+−+⋅−−
22
1)4
2
5
(arccos)
2
5
45( .
В примерах 11 и 12 продемонстрировано применение теории
интегрирования рациональных дробей. Напомним, что дробь, в числителе
и знаменателе которой находятся многочлены, называется рациональной
дробью. Пусть )(xP
n
− многочлен степени
n
, )(xQ
m
− многочлен степени
m
, тогда
)(
)(
)(
xQ
xP
xR
m
n
= − рациональная дробь. Если
m
n
<
, то рациональная
дробь называется правильной, а в противном случае (т.е. если выполнено
неравенство
m
n
≥
) неправильной. Всякую неправильную рациональную
дробь можно представить в виде суммы двух слагаемых: многочлена и
правильной рациональной дроби. Поэтому надо уметь интегрировать
правильные рациональные дроби. Дроби вида
( )
α
ax
A
−
и
( )
β
qpxx
NMx
++
+
2
,
где
N
M
A
q
p
a
,
,
,
,
,
− вещественные числа,
β
α
,
− натуральные числа,
04
2
<− qp (т.е. уравнение 0
2
=++ qpxx не имеет вещественных корней),
называются элементарными рациональными дробями. Справедливо
утверждение:
Теорема о разложении правильной рациональной дроби. Всякую
правильную рациональную дробь можно представить в виде суммы
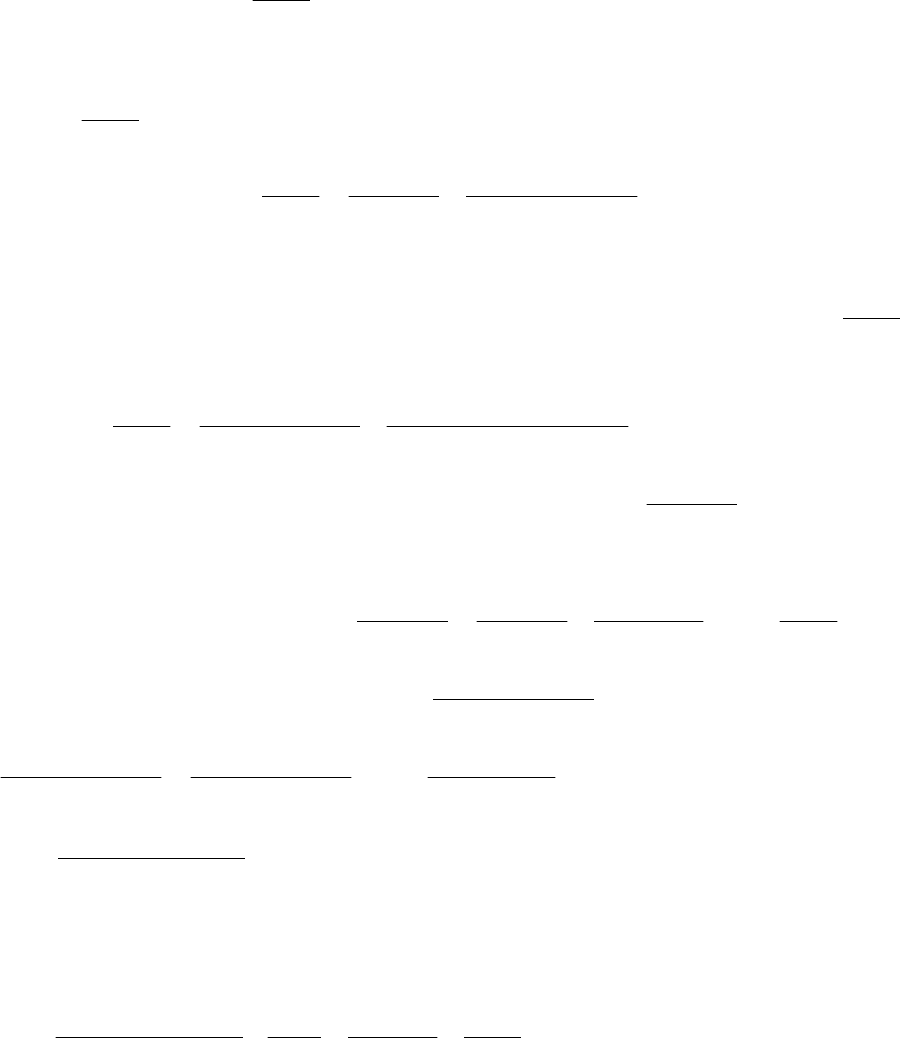
115
элементарных рациональных дробей.
При практическом применении этой теоремы полезны следующие
утверждения (
)(
)(
)(
xQ
xP
xR = − правильная рациональная дробь):
1. Пусть 1,0)(),()()(
11
≥≠−= kaQxQaxxQ
k
. Тогда правильная дробь
)(
)(
)(
xQ
xP
xR = может быть представлена в виде суммы правильных дробей
следующим образом:
)()(
)(
)(
)(
)(
1
1
1
xQax
xP
ax
A
xQ
xP
kk −
−
+
−
= .
2. Пусть 1,04),()()(
2
1
2
≥<−++= kqpxQqpxxxQ
k
, и многочлен )(
1
xQ
не делится на многочлен qpxx ++
2
. Тогда правильная дробь
)(
)(
)(
xQ
xP
xR =
может быть представлена в виде суммы правильных дробей следующим
образом:
)()(
)(
)(
)(
)(
1
12
1
2
xQqpxx
xP
qpxx
NMx
xQ
xP
kk −
++
+
++
+
= .
Из этих утверждений следует, в частности, что если
k
ax
xP
)(
)(
−
- правильная
рациональная дробь, то существуют такие числа
k
AA ,,
1
L
, что
справедливо равенство
ax
A
ax
A
ax
A
ax
xP
k
k
k
k
k
−
++
−
+
−
=
−
−
−
1
1
1
)()()(
)(
L
, а
правильную рациональную дробь
k
qpxx
xP
)(
)(
2
++
можно представить так
qpxx
NxM
qpxx
NxM
qpxx
xP
k
kk
k
++
+
++
++
+
=
++
2
11
22
)()(
)(
L
.
11.
dx
xx
xx
2
2
3)1)((
38366
+−
−−−
∫
Для того, чтобы найти этот интеграл, применяем теорему о
разложении правильной рациональной дроби на сумму простейших
дробей:
2
2
3)1)((
38366
+−
−−−
xx
xx
=
3
)3(
1
2
+
+
+
+
− x
C
x
B
x
A
.
Находим
C
B
A
,
,
из следующего равенства:
)3)(1()1()3(38366
22
+−+−++=−−− xxCxBxAxx
Подставляем
1
=
x
в обе части предыдущего равенства и находим
A
16
80
=
−
, откуда
5
−
=
A
. Подставляем
3
−
=
x
в обе части предыдущего
равенства и находим
B
4
38
)
3
(
36
9
6
−
=
−
−
⋅
−
⋅
−
, откуда
4
−
=
B
.
Приравнивая коэффициенты при
2
x
, получаем равенство
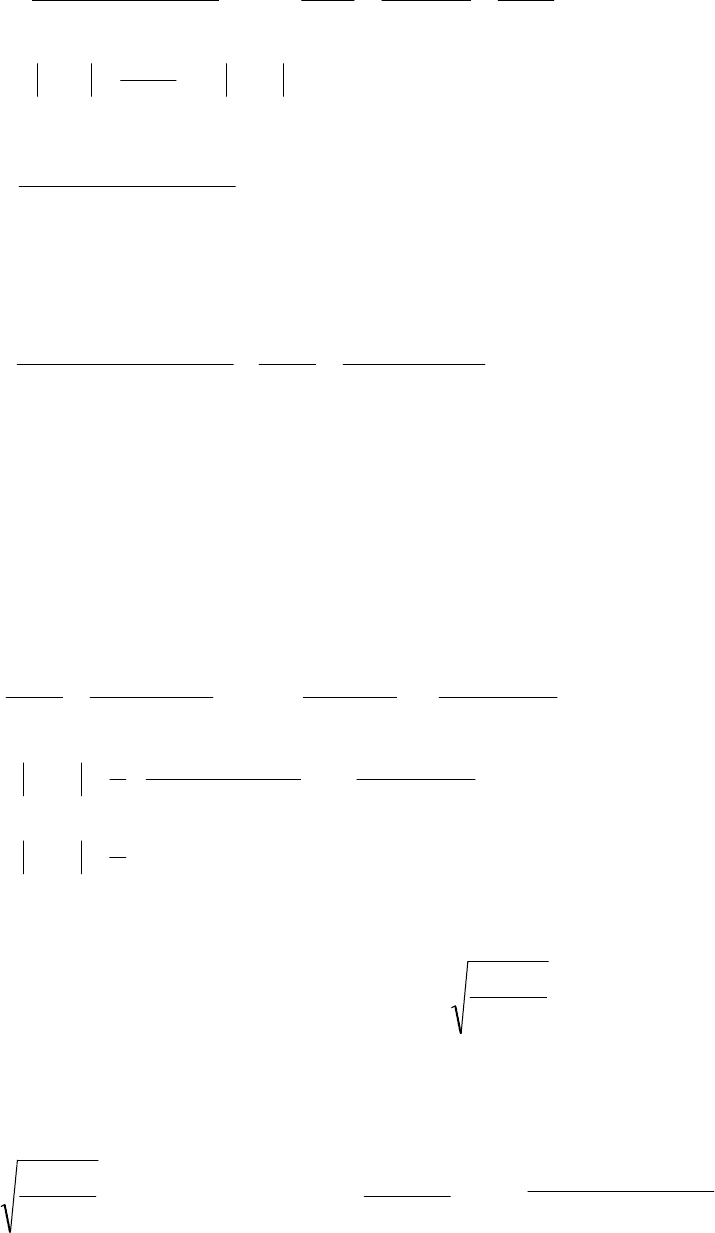
116
C
C
A
+
−
=
+
=
−
5
6
, откуда следует, что
1
−
=
C
. Итак, используя
теорему о разложении правильной рациональной дроби на сумму
простейших дробей, получили
dx
xx
xx
2
2
3)1)((
38366
+−
−−−
∫
= dx
x
x
x
∫
+
−
+
+
−
+
−
−
3
1
)3(
4
1
5
2
=
=
Cx
x
x ++−
+
+−− 3ln
3
4
1ln5 .
12.
dx
xxx
xx
3)22)((
774
2
2
+++
++
∫
=
Для того, чтобы найти этот интеграл, применяем теорему о
разложении правильной рациональной дроби на сумму простейших
дробей:
3)22)((
774
2
2
+++
++
xxx
xx
=
)32(
2
2
++
+
+
+
xx
CBx
x
A
.
Находим
C
B
A
,
,
из следующего равенства:
)2)(()32(774
22
+++++=++ xCBxxxAxx
Подставляем
2
−
=
x
в обе части предыдущего равенства и находим
A
3
9
=
,
откуда
3
=
A
. Приравниваем коэффициенты при
2
x
:
B
B
A
+
=
+
=
3
4
.
Отсюда следует, что
1
=
B
. Приравниваем коэффициенты при
0
x
:
C
C
A
2
9
2
3
7
+
=
+
=
. Отсюда следует, что
1
−
=
C
. Теперь можем найти
интеграл
=
dx
xx
x
x
∫
++
−
+
+
32
1
2
3
2
=
∫∫
++
−
+
+
+
+
dx
x
x
x
xd
1)1(
2)1(
2
)2(
3
2
=
∫∫
++
+
−
++
++
++=
1)1(
)1(
2
1)1(
)1)1((
2
1
2ln3
22
2
x
xd
x
xd
x =
Cxarctgxx ++−++++= )1(2)1)1ln((
2
1
2ln3
2
.
Рассмотрим некоторые приемы интегрирования функций, содержащих
радикалы. Пусть требуется найти
dx
x
x
xR
m
∫
+
+
δγ
βα
, , где
R
− рациональная
функция от двух аргументов,
m
− натуральное число,
δ
γ
β
α
,
,
,
−
константы, удовлетворяющие условию
0
≠
−
βγ
αδ
. В этом случае делаем
следующую замену переменной:
m
x
x
t
δγ
βα
+
+
=
,
отсюда находим
m
m
t
t
x
γα
βδ
−
−
=
,
(
)
( )
dt
t
tm
dx
m
m
γα
βγαδ
−
−
=
−
1
,
после
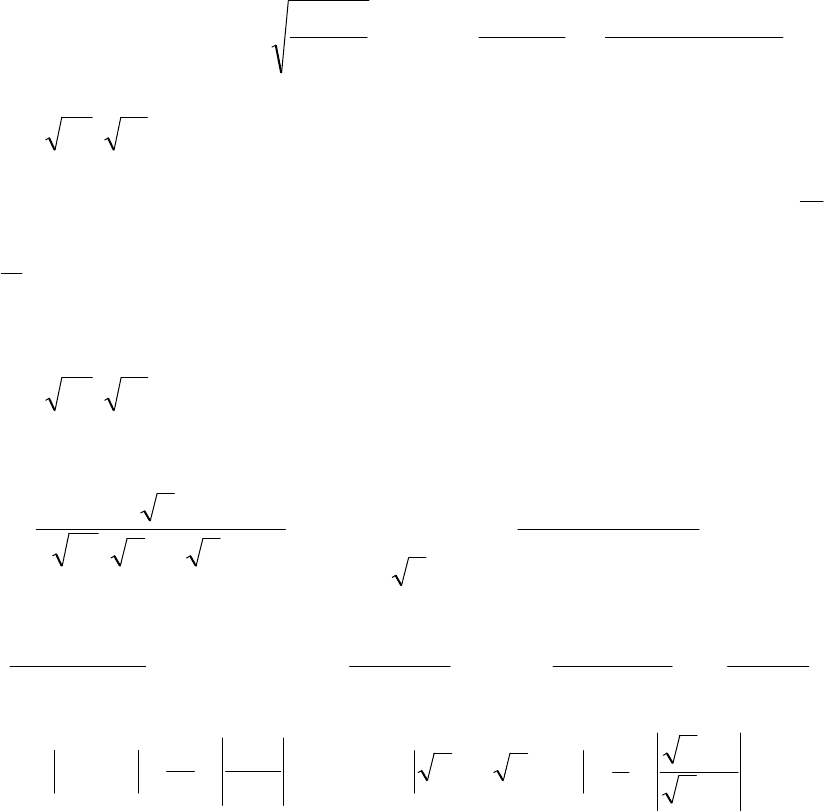
117
этого получаем dx
x
x
xR
m
∫
+
+
δγ
βα
, =
(
)
( )
∫
−
−
−
−
−
dt
t
tm
t
t
t
R
m
m
m
m
γα
βγαδ
γα
βδ
1
, , т.е.
получили интеграл от рациональной дроби. Если надо найти
(
)
dxxxxR
n
l
m
k
∫
,, ,
n
m
,
− натуральные числа, то вначале находим
наименьшее общее кратное чисел
m
и
n
. Пусть это будет
p
. Тогда
1
m
m
p
=
и
1
n
n
p
= натуральные числа, следовательно замена переменной
p
t
x
=
позволяет избавится от иррациональностей. Действительно, в этом случае
(
)
∫∫
−
= dtpttttRdxxxxR
p
lnkm
p
n
l
m
k 1
),,(,,
11
, т.е. получили интеграл от
рациональной дроби.
13.
dx
xxx
x
27)6(6
2710
63
6
5
6
−+
−−
∫
=
=
=
=
6
5
6
6
xt
dttdx
tx
=
∫
−+
−
−
dtt
ttt
t
5
25
6
)276(6
2710
=
=
∫
−+
−
−
dt
t
t
36)3(
2710
2
=
=
−=
+
=
dzdt
zt
tz
3
3
=
∫
−
+
−
dz
z
z
36
310
2
=
∫ ∫
−
+
−
−
−
222
2
6
3
36
)36(
5
z
dz
z
zd
=
=
C
z
z
z +
+
−
+−−
6
6
ln
12
3
36ln5
2
= C
x
x
xx +
+
−
+−+−
9
3
ln
4
1
276ln5
6
6
63
.
При интегрировании выражений вида
x
x
mn
cos
sin
⋅ , где
m
n
,
- целые
числа, следует различать случаи:
1.
1
2
+
=
k
n
, т.е.
n
- нечетное число. Тогда =⋅
∫
dxxx
mn
cossin
∫∫
⋅⋅=⋅=
+
dxxxxdxxx
mkmk
cos)(sinsincossin
212
= =−=
∫
)cossin( xdxx
∫∫
=⋅−−===⋅−−=
L
dtttxtxdxxx
mkmk
)1()cos(coscos)cos1(
22
Т.е. в этом случае вносим
x
sin
под знак дифференциала и получаем
интеграл от многочлена.
2.
1
2
+
=
l
m
, т.е.
m
- нечетное число. Действуем аналогично предыдущему,
но под знак дифференциала вносим
x
cos
:
=⋅
∫
dxxx
mn
cossin
=⋅=
∫
+
dxxx
ln 12
cossin =⋅⋅
∫
dxxxx
in
cos)(cossin
2
==
∫
)sincos( xdxx
===−⋅=
∫
)sin(sin)sin1(sin
2
xtxdxx
ln
L
=−⋅
∫
dttt
ln
)1(
2
3. Если
n
и
m
- четные числа, т.е.если
l
m
k
n
2
,
2
=
=
,
тогда следует
применить формулы ”удвоения аргумента”:
.2cos1sin2,2cos1cos2
22
αααα
−=+=
В этом случае получаем

118
=⋅
∫
dxxx
mn
cossin
=⋅
∫
dxxx
lk 22
cossin
.
2
2cos1
2
2cos1
∫
+
⋅
−
dx
xx
lk
После чего выполняем алгебраические преобразования и вновь, если
необходимо, применяем вышеописанную процедуру.
В примерах 14-15 показано как можно интегрировать произведение
функций
x
sin
и
x
cos
:
14.
dxxx 2)(5
cos
2)(5
sin
42
++
∫
=
=
)25(2)(5
cos
2)(5
sin
5
1
42
+⋅++
∫
xdxx =
[
]
25
+
=
xt =
=
tdtt
cossin
5
1
42
∫
= dt
tt
2
2
2cos1
2
2cos1
5
1
+
⋅
−
∫
=
∫
+− dttt )2cos1)(2cos1(
40
1
2
=
=
∫
+⋅ dttt )2cos1(2sin
40
1
2
=
∫∫
+− )2(sin2sin
80
1
)4cos1(
80
1
2
ttddtt =
=
1
3
2sin
3
1
4sin
4
1
80
1
Cttt +
+− =
Cxx
x
++++− )410(sin
240
1
)820sin(
320
1
16
3
.
15.
dx
x
x
1)(4
cos
1)(4
sin
8
3
−
−
∫
=
=
+=
−
=
4/
4/)1(
14
dtdx
tx
xt
= dt
t
t
t
cos
sin
sin
4
1
8
2
⋅
∫
=
=
)(cos
cos
cos1
4
1
8
2
td
t
t
−
−
∫
=
[
]
tz cos
=
=
∫
−−
−− dzzz )(
4
1
68
= C
z
z
+−
57
20
1
28
1
=
=
C
xx
+
−
−
− )14(cos20
1
)14(cos28
1
57
.
Если подинтегральное выражение является рациональной дробью от
tgx
(или от
ctgx
), то замена переменной вида
tgx
t
=
(соответственно
ctgx
t
=
) приведет к интегралу от рациональной дроби аргумента
t
:
16.
=
−
−
=
+
⋅
−
+
=
+=
=
=
=
−
+
∫∫∫
32
)32(
2
1
1
32
1
)1/(
32
1
2
2
2
2
t
td
t
dt
t
t
tdtdx
arctgtx
tgxt
dx
tgx
tg
=
CtgxCt +−=+− |32|ln
2
1
|32|ln
2
1
.
Если требуется найти интеграл от рациональных дробей, аргументами
которых являются тригонометрические функции
x
sin
и
x
cos
, то часто
применяется универсальная тригонометрическая подстановка:
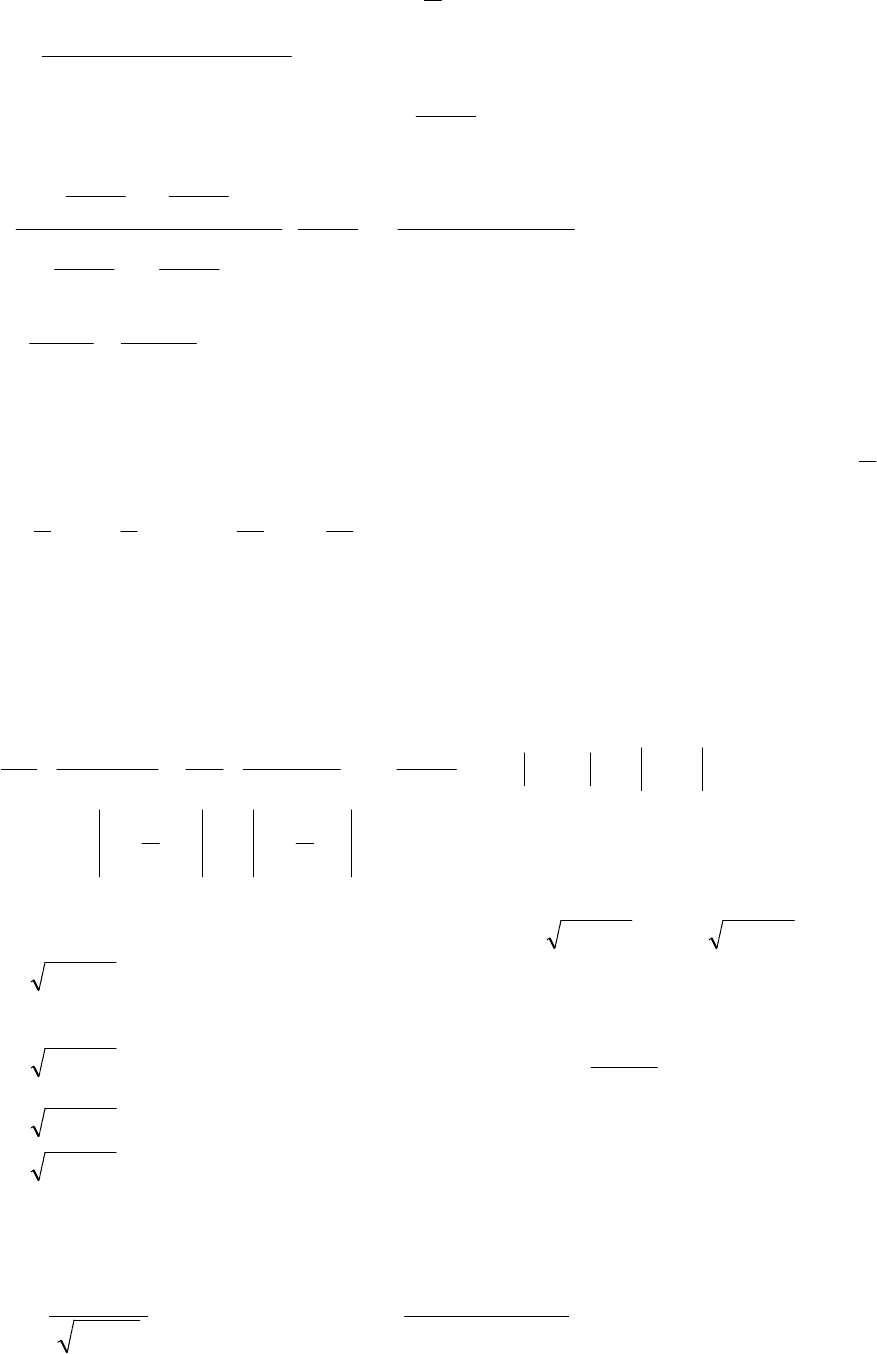
119
17.
dx
x
x
xx
2
cos
2
sin
3
12cos3sin11
+
+
−
−
−
∫
=
+
=
=
=
1
2
2
2
2
t
dt
dx
tarctgx
x
tgt
=
=
1
2
2
1
1
2
1
2
3
12
1
1
3
1
2
11
2
2
2
2
2
2
2
+
⋅
+
+
−
+
+
−
+
−
−
+
−
∫
t
dt
t
t
t
t
t
t
t
t
=
dt
tt
tt
2
)1()46(
15229
2
2
∫
+⋅+
−−−
=
=
dt
t
CBt
t
A
∫
+
+
+
+
1
23
2
=
Находим
C
B
A
,
,
из равенства )23()()1(15229
22
+⋅+++=−−− tCBttAtt .
Сначала в обе части этого равенства подставляем
3
2
−=t :
⇒⋅=−=−⋅+⋅−
9
13
3
13
15
3
2
22
9
4
9 A
3
−
=
⇒
A
. Затем приравниваем коэффициенты при
2
t
и при
0
t
:
23339:
2
−=⇒+−=+=− BBBAt .
623215:
0
−=⇒+−=+=− CCCAt .
Теперь продолжаем:
=
∫∫∫
+
−
+
+−
+
+
+−
1
6
1
)1(
2
2
2
3
)23(
3
3
22
2
t
dt
t
td
t
td
=
Ctarctgtt +−+−+− 61ln23ln
2
=
=
Cx
x
tg
x
tg +−+−+− 31
2
ln2
2
3ln
2
.
При интегрировании выражений вида
),(
22
xaxR −
,
),(
22
xaxR +
,
),(
22
axxR −
можно применять тригонометрические подстановки,
позволяющие избавиться от квадратного корня. Для выражений вида
),(
22
axxR −
делаем замену переменной
t
a
x
sin
1
= , для выражений
),(
22
xaxR +
осуществляем замену
tgt
a
x
⋅
=
, и, наконец для выражений
),(
22
xaxR −
применяем подстановку
t
a
x
sin
=
, как это показано в
следующем примере
18
. tdt
t
tt
xt
tdtdx
tx
dx
x
xx
cos
cos
sin4sin5
arcsin
cos
sin
1
45
2
2
2
⋅
−
=
=
=
=
=
−
−
∫∫
=
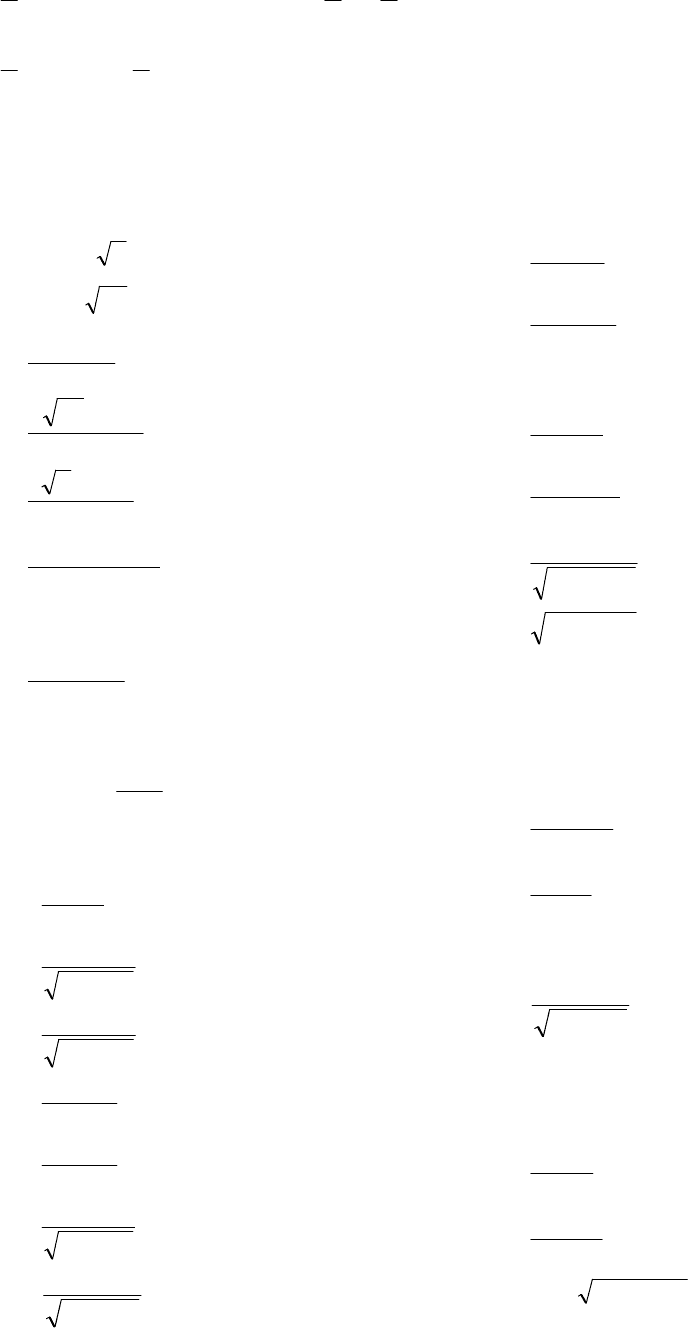
120
=
∫ ∫
−− tdtdtt sin4)2cos1(
2
5
=
Cttt ++− cos42sin
4
5
2
5
=
=
Cxxx ++− )cos(arcsin4)arcsin2sin(
4
5
arcsin
2
5
.
Задачи для самостоятельного решения.
Найти неопределенные интегралы:
1.
( )4
3
x x dx−
∫
;
2.
( )x x dx
2 23 2
+
∫
;
3.
3 4
2
3
x x
x
dx
−
∫
;
4.
2 3
34 5
2
x x
x
dx
−
∫
;
5.
3 4
2
3
x x
x
dx
+
∫
;
6.
3 4
2
3
x x x
x
dx
sin −
∫
;
7.
( )2
2
x
x dx+
∫
;
8.
8 3
3
3
x x
x
x
dx
+
∫
;
9.
( cos )2 3x e dx
x
−
∫
;
10.
( )tg x
tg x
dx
2
2
1
+
∫
;
11.
( sin )3 10x dx−
∫
;
12.
cos
sin
2
2
x
x
dx
∫
;
13.
dx
x4 4
2
−
∫
;
14.
dx
x4 4
2
+
∫
;
15.
dx
x
4
4
2
+
∫
;
16.
dx
x
4
4
2
−
∫
;
17.
dx
x4 9
2
−
∫
;
18.
dx
x8 3
2
+
∫
;
19.
dx
x
3
2
2
+
∫
;
20.
dx
x
4
25
2
−
∫
;
21.
( )3 2
11
x dx−
∫
;
22.
dx
x
5
7
+
∫
;
23.
dx
x(2 )+
∫
3
5
;
24.
dx
x( )8 5
4
3
−
∫
;
25.
( )7 2
3
4
x dx−
∫
;
26.
sin( )3 4x dx−
∫
;
27.
cos( )4 −
∫
x dx
;
28.
e dx
x
− +
∫
7 12
;
29.
dx
xsin ( )
2
5
∫
;
30.
xdx
x
2
5
+
∫
;
31.
x x dx( )
2 21
7+
∫
;
32.
x
x
dx
8 4
2
−
∫
;
33.
x x dxsin( )2 3
2
+
∫
;
34.
x dx
x
2
2
3
−
∫
;
35.
x dx
x
2
6
9
+
∫
;
36.
x dx
x
3
8
16
−
∫
;
37.
cos sinx x dx9 2−
∫
;
