Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

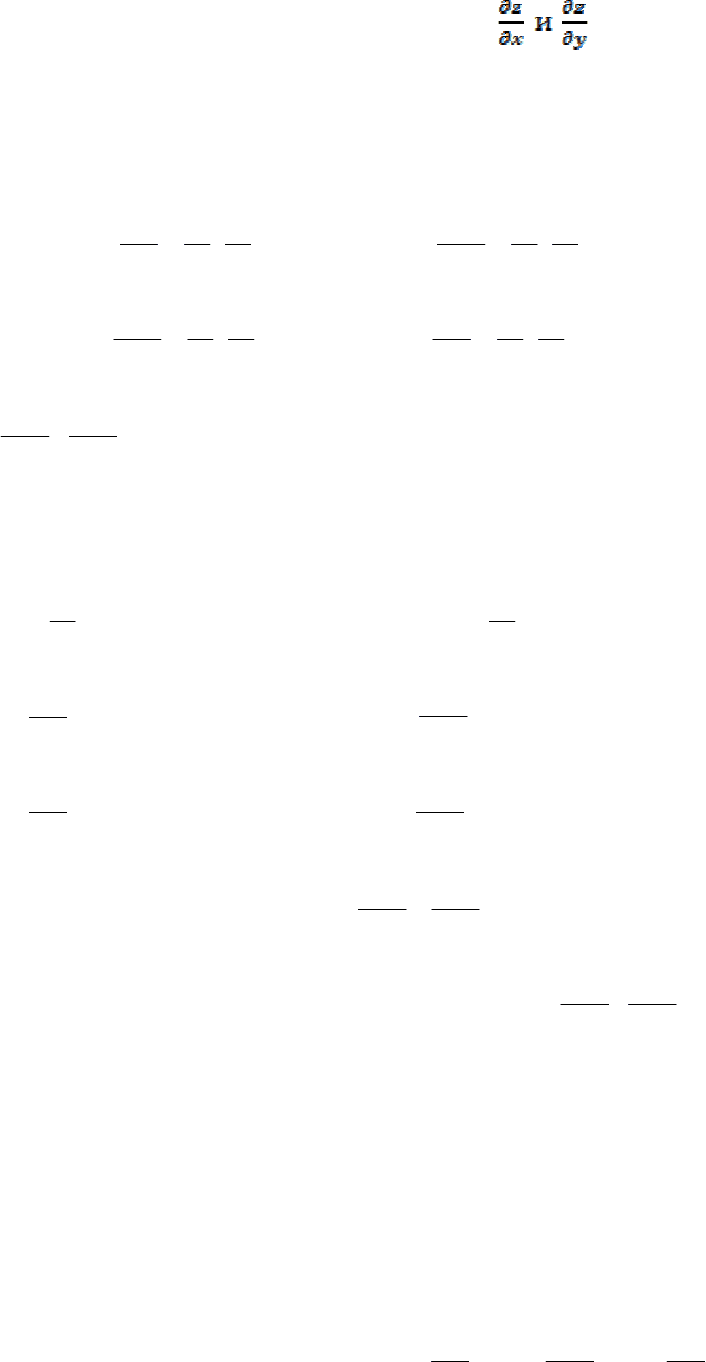
141
z = f (x;y), определенная на множестве G, называются частными
производными I порядка.
Частными производными II порядка функции z = f(x; y) называется част-
ные производные от частных производных первого порядка:
z
x
z
x
x
z
′′
=
∂
∂
∂
∂
=
∂
∂
2
2
xx
,
z
x
z
yyx
z
′′
=
∂
∂
∂
∂
=
∂∂
∂
2
x
z
y
z
xxy
z
′′
=
∂
∂
∂
∂
=
∂∂
∂
2
yx
,
z
y
z
y
y
z
′′
=
∂
∂
∂
∂
=
∂
∂
2
2
yy
xy
z
yx
z
∂∂
∂
∂∂
∂
22
;
– называются смешанными производными.
Пример 8. Найти все частные производные первого и второго порядка для
функции z = cos(x;y):
( ) ( )
′
⋅⋅⋅−=
∂
∂
yxyx
x
z
sin
x
=
(
)
xyy
sin
−
,
( ) ( )
′
⋅−=
∂
∂
xyxy
y
z
sin
y
=
(
)
xyx
sin
−
,
( )( )
′
−=
∂
∂
xyy
x
z
sin
2
2
x
=
(
)
xyy cos
2
−
,
( )( )
′
−=
∂∂
∂
xyy
yx
z
sin
2
y
=
(
)
(
)
xxyyxy
cossin1
−
⋅
−
( )( )
′
−=
∂
∂
xyx
y
z
sin
2
2
y
=
(
)
xyx cos
2
−
,
( )( )
′
−=
∂∂
∂
xyx
xy
z
sin
2
x
=
(
)
(
)
уxyxxy
cossin1
−
⋅
−
,
xy
z
yx
z
∂∂
∂
=
∂∂
∂
22
.
Имеет место утверждение: если производные
xy
z
и
yx
z
∂∂
∂
∂∂
∂
22
существуют и не-
прерывны в некоторой окрестности т. М и непрерывны в самой т. М, то они
равны.
Дифференцируя частные производные II порядка по x и по y , получим ча-
стные производные III порядка.
Полный дифференциал II порядка некоторой функции – это полный
дифференциал от ее полного дифференциала.
(
)
dzdzd =
2
:
2
2
22
2
2
2
2
2 dy
y
z
dxdy
yx
z
dx
x
z
zd
∂
∂
+
∂∂
∂
+
∂
∂
=
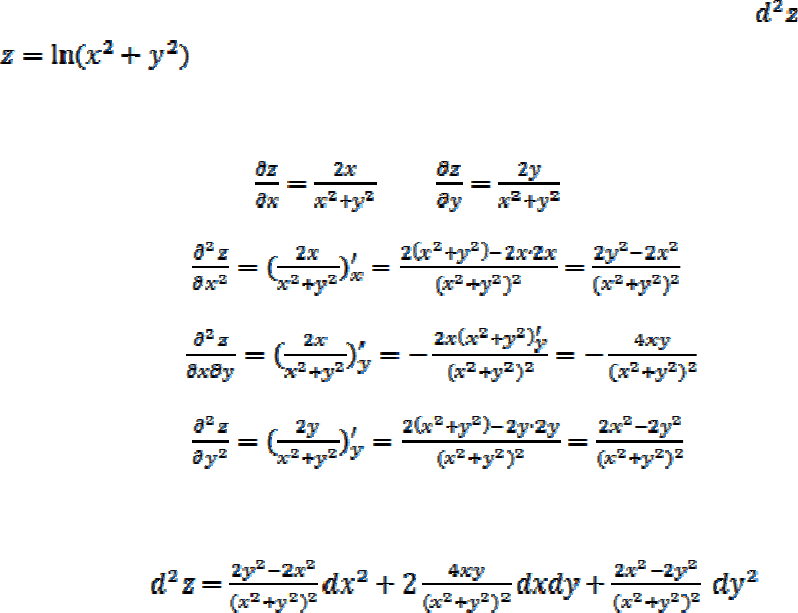
142
Полным дифференциалом n-го порядка функции z = f(x; y) называется пол-
ный дифференциал от полного дифференциала (n-1)-го порядка.
Пример 9. Найти дифференциал II порядка
функции
.
Находим частные производные первого и второго порядка:
, ,
,
,
,
Подставляя в формулу, получим:
.
Экстремумы функций двух переменных. Пусть функция z = f(x; y) опре-
делена в некоторой окрестности точки M
0
(x
o,
y
o
). Точка M
0
(x
o
;y
o
) называется
точкой максимума (минимума) функции z = f(x; y), если существует такая
окрестность т. M
0
,
в которой
для любой т. M(x;y) выполняется условие
f(x;y)
≤
f(x
o
;y
o
) [f(x;y)
≥
f(x
o
;y
o
)].
Точки максимума и минимума функции называются точками экстремума.
Необходимое условие экстремума. Если дифференцируемая функция z =
f(x; y) имеет в т. M
0
(x
o
; y
o
) экстремум, то частные производные первого
порядка в этой точке равны нулю.
Также экстремум функции 2-х переменных может быть в точках, в кото-
рых частные производные первого порядка равны нулю, или не существуют.
Такие точки называются стационарными.
Пример 10. Найти стационарные точки функции
xyyxz 3
33
−−=
.
Находим частные производные первого порядка:
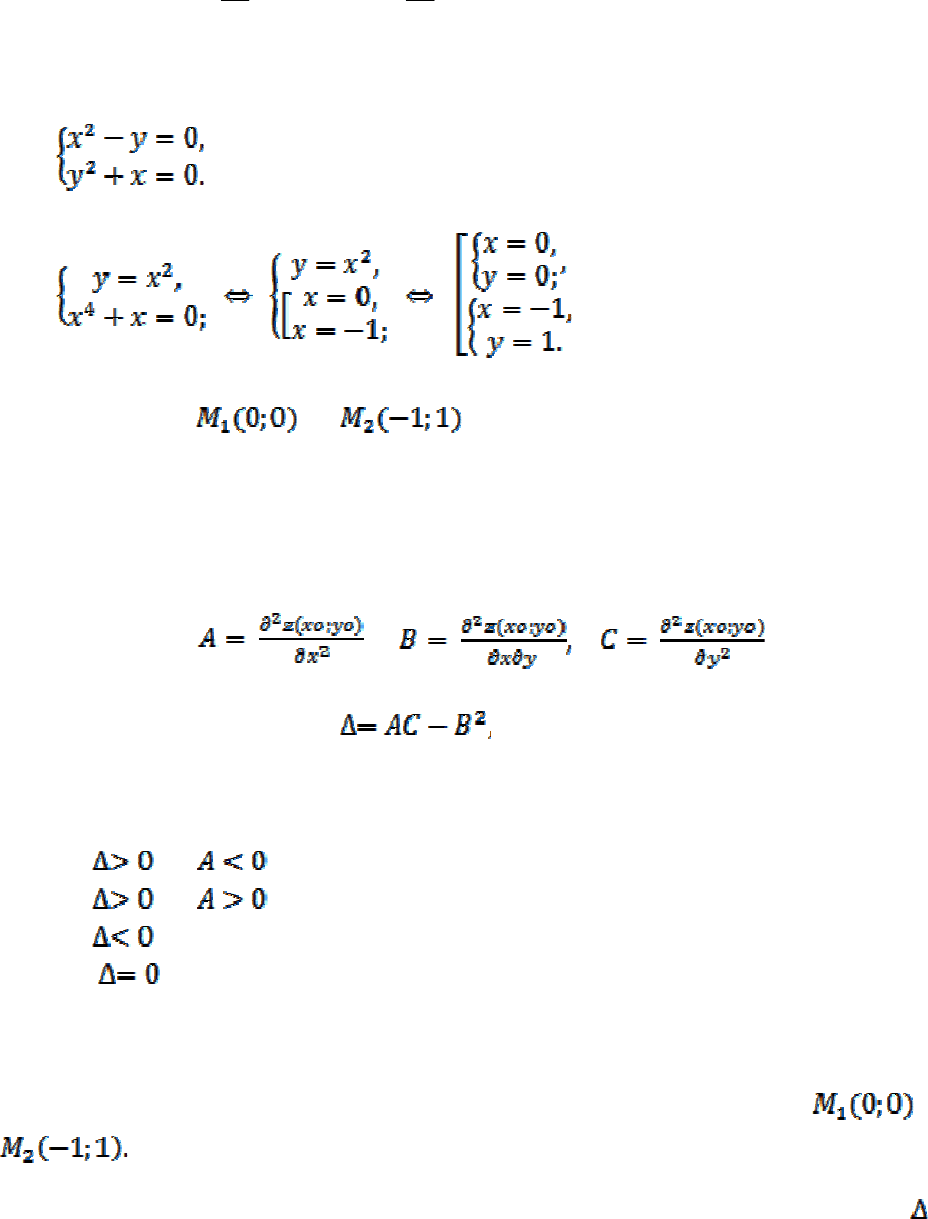
143
xy
dy
dz
yx
dx
dz
33 ,33
22
−−=−=
.
Находим стационарные точки, используя необходимые условия:
Получаем
и стационарные точки.
Достаточные условия экстремума функции двух переменных.
Пусть M
0
(x
o
;y
o
) стационарная точка функции z = f(x; y). Обозначим
, .
Cоставим выражение
тогда достаточные условия экстрему-
ма функции двух переменных z = f(x; y) в точке M
0
(x
o
;y
o
) запишутся в следую-
щем виде:
и , то M
0
(x
o
;y
o
) – точка максимума.
и , то M
0
(x
o
;y
o
) – точка минимума.
, то M
0
(x
o
;y
o
) не является точкой экстремума.
, то точка M
0
(x
o
;y
o
) может как быть, так и не быть точкой
экстремума, поэтому требуется дополнительное исследование.
Пример11. Исследовать на экстремум функцию
xyyxz 3
33
−−=
.
В предыдущем примере найдены стационарные точки
и
Найдем частные производные второго порядка и составим выражение
:
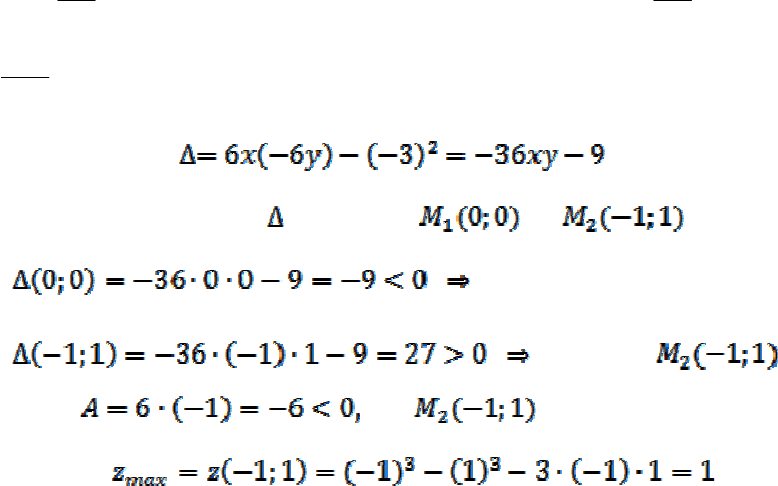
144
,6)33(
2
2
2
xyx
x
z
A
x
=
′
−=
∂
∂
=
,6)33(
2
2
2
yxy
y
z
C
y
−=
′
−−=
∂
∂
=
( )
333
2
2
−=
′
−=
∂∂
∂
=
y
yx
yx
z
B
.
Вычислим значения
в точках и :
экстремума нет.
в точке экстремум
есть, т.к.
то - точка максимума.
Найдем
.
Условный экстремум функции двух переменных. Рассмотрим задачу о на-
хождении экстремума функции z = f(x y) при условии, что переменные x,y
связаны соотношением
(
)
0,
=
yx
ϕ
. Такой экстремум называется условным в
отличие от рассмотренного ранее.
Возможны два случая:
1) уравнение
(
)
0,
=
yx
ϕ
определяет функцию y=y(x) (т.е. разрешимо отно-
сительно переменной y), тогда функция z = f(x; y(x)) – будет функцией одной
переменной и задача отыскания условного экстремума функции двух перемен-
ных сводится к задаче отыскания экстремума функции одной переменной.
2) уравнение
(
)
0,
=
yx
ϕ
не разрешимо относительно переменной y.
В этом случае применяется метод множителей Лагранжа. Составляется
функция Лагранжа:
(
)
(
)
(
)
yxyxfyxL
;;,,
λϕ
λ
+
=
, где λ – параметр, называемый
множителем Лагранжа, и исследуется на обычный экстремум.
Необходимые условие экстремума. Стационарные точки находим решая
систему уравнений:
(
)
( )
( )
=
′
=
=
.0,,
,0,,'
,0,,
'
λ
λ
λ
λ
yxL
yxL
yxL
y
x
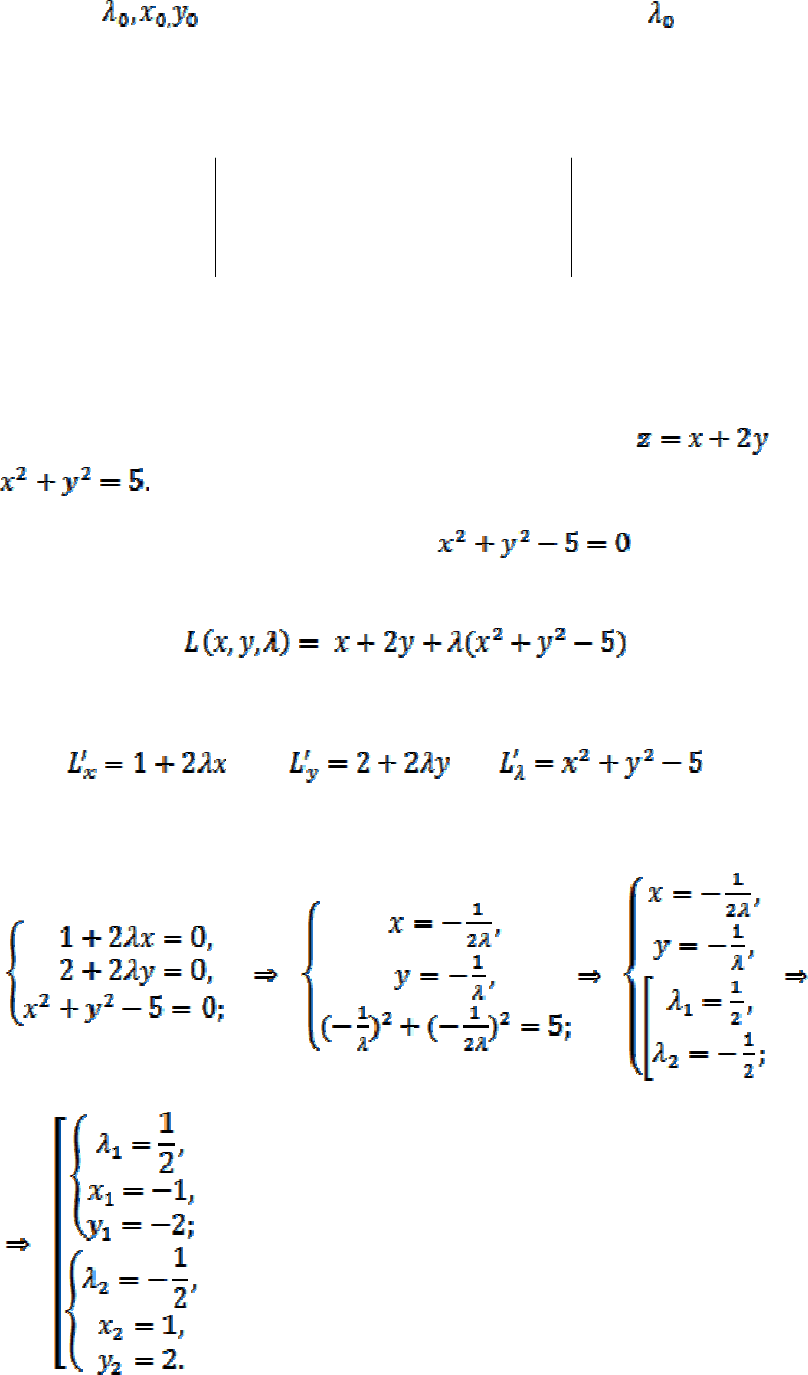
145
Пусть - решения системы, т.е. значению соответствует ста-
ционарная точка M
0
(x
o
;y
o
).
Достаточное условие экстремума. Составляем определитель
(
)
(
)
( ) ( ) ( )
( ) ( ) ( )
00
"
00
"
00
000000
'
00
'
00
'
0
λλλϕ
λλλϕ
λϕλϕ
MLMLM
MLMLM
MM
yyxy
y
xyxx
x
yx
′
′′′′
−=∆
.
Если
0
<
∆
, то функция z = f(x; y) имеет в т. М
0
условный максимум.
Если
0
>
∆
, то функция z = f(x; y) имеет в т. М
0
условный минимум.
Пример 12. Найти условный экстремум функции
при усло-
вии
Запишем уравнение связи в виде
и составим функцию
Лагранжа:
.
Находим частные производные функции:
, .
Составляем и решаем систему:
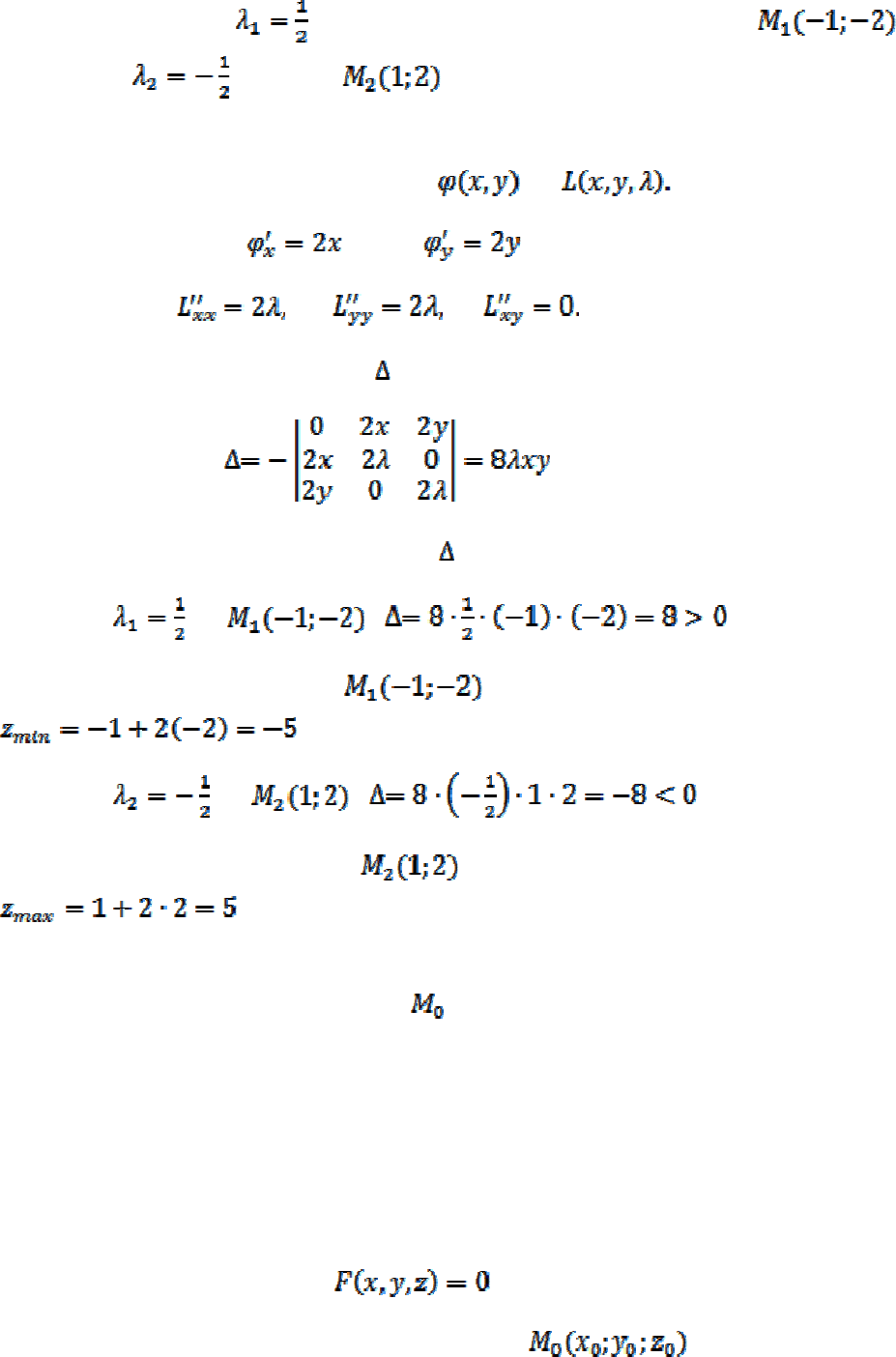
146
Т.е. значению соответствует стационарная точка , а
значению
- точка .
Проверяем достаточные условия: для этого найдем частные производные
первого и второго порядка функций
и
, ,
Составляем определитель
:
.
Найдем значение определителя
для каждой из стационарных точек.
Для
и .
Это значит, что в точке
функция имеет условный минимум и
.
Для
и .
Это значит, что в точке
функция имеет условный максимум и
.
Геометрические приложения частных производных. Касательной плоско-
стью к поверхности в ее точке
(точка касания) называется плоскость,
содержащая в себе все касательные к кривым, проведенным на поверхности
через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к каса-
тельной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид
,
то уравнение касательной плоскости в точке
имеет вид
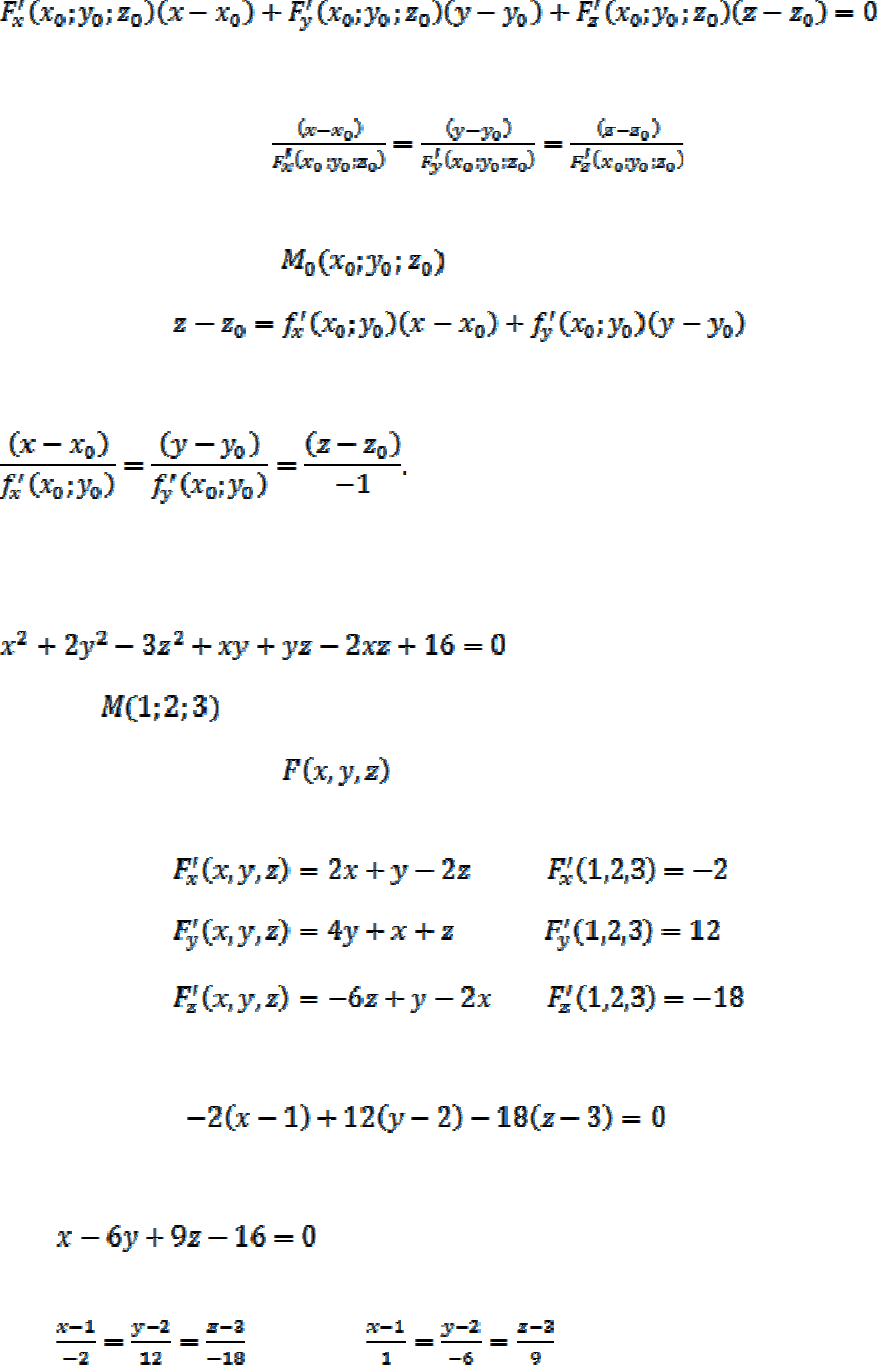
147
.
Уравнения нормали:
.
Если поверхность задана в явной форме z = f(x y), то уравнение касатель-
ной плоскости в точке
имеет вид
,
а уравнение нормали -
Пример 13. найти уравнения касательной плоскости и нормали к поверх-
ности
в точке
.
Обозначив через
левую часть уравнения поверхности, найдем
частные производные и их значения в точке М.
, ;
, ;
, .
Подставляя в формулы, получим
или
- уравнение касательной плоскости,
, или
- уравнения нормали.
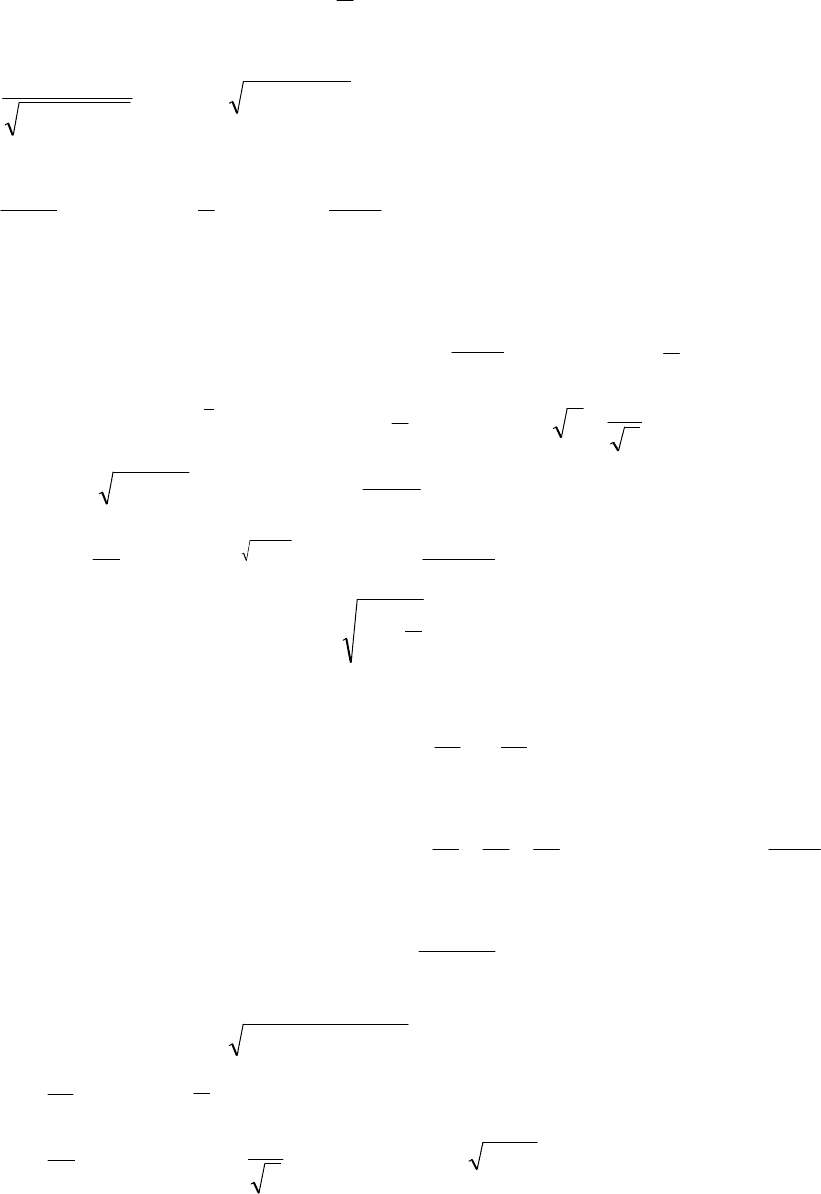
148
Задачи для самостоятельного решения.
1.
Выразить объем конуса V как функцию его образующей x и радиуса ос-
нования у.
2.
Выразить площадь S боковой поверхности правильной четырехугольной
пирамиды как функцию ее высоты x и бокового ребра у.
3.
Найти,
f
( ; )
−
11
если
f x y xy
x
y
( , ) = +
.
4.
Найти область существования функции:
а)
z
x y
=
− −
1
4
2 2
; б)
z x y= − −
1
2 2
; в)
z
x
y
=
+
arccos
.
5.
Найти пределы функций:
а)
x o
y
xy
x
→
→2
lim
sin
; б)
x
y k
x
y
x
→∞
→
+
lim
1
; в)
x o
y
x
x y
→
→
+
0
lim
.
6.
Найти частные производные функций:
а)
z x y x y xy x= + − + − +
3 3 2 2
3 5 6 1
; б)
z
x y
x y
=
−
+
; в)
z
y
x
=
;
г)
z
x
y
=
; д)
z
e
y
x
=
sin
; е)
z arctg
y
x
=
; ж)
z x y
y
x
= +
;
з)
z x x y= + +
ln( )
2 2
; и)
z arctg
x y
xy
=
+
−1
; к)
z x y y x= +sin ( cos sin )
2 2 2
;
л)
z arctg
x
y
=
3
; м)
z
e
x y
=
− +
2 2
; н)
z
x y
x y
=
−
+
cos
2 2
; о)
u xy
z
= ( )
; п)
u
z
xy
=
.
7.
Найти
z
x
′
( ; )2 1
и
z
y
′
( ; )2 1
, если
z xy
x
y
= +
.
8. Найти
u
x
′
( ; ; )1 2 0
,
u
y
′
( ; ; )1 2 0
,
u
z
′
( ; ; )1 2 0
, если
u xy z
=
+
ln( )
.
9. Проверить справедливость равенства
x
z
x
y
z
y
∂
∂
∂
∂
+ = 2
, если
z x xy y= + +ln( )
2 2
.
10. Проверить справедливость равенства
∂
∂
∂
∂
∂
∂
u
x
u
y
u
z
+ + = 1
, если
u x
x y
y z
= +
−
−
.
11. Найти полные дифференциалы следующих функций:
а)
z x y xy= + −
3 3
3
; б)
z x y=
3 2
; в)
z
x y
x y
=
−
+
2 2
2 2
; г)
z x y= +ln( )
2 2
.
12.
Вычислить приближенно:
а)
( , ) ( , )1 02 0 97
3 2
⋅
; б)
( , ) ( , )4 05 2 93
2 2
+
; в)
sin
cos
32
59
o o
⋅
.
13.
Найти
dz
dt
, если
z
x
y
=
, где
x e y t
t
= =, ln
.
14.
Найти
du
dt
, если
u
x
y
= ln sin
, где
x t y t= = +3 1
2 2
,
.
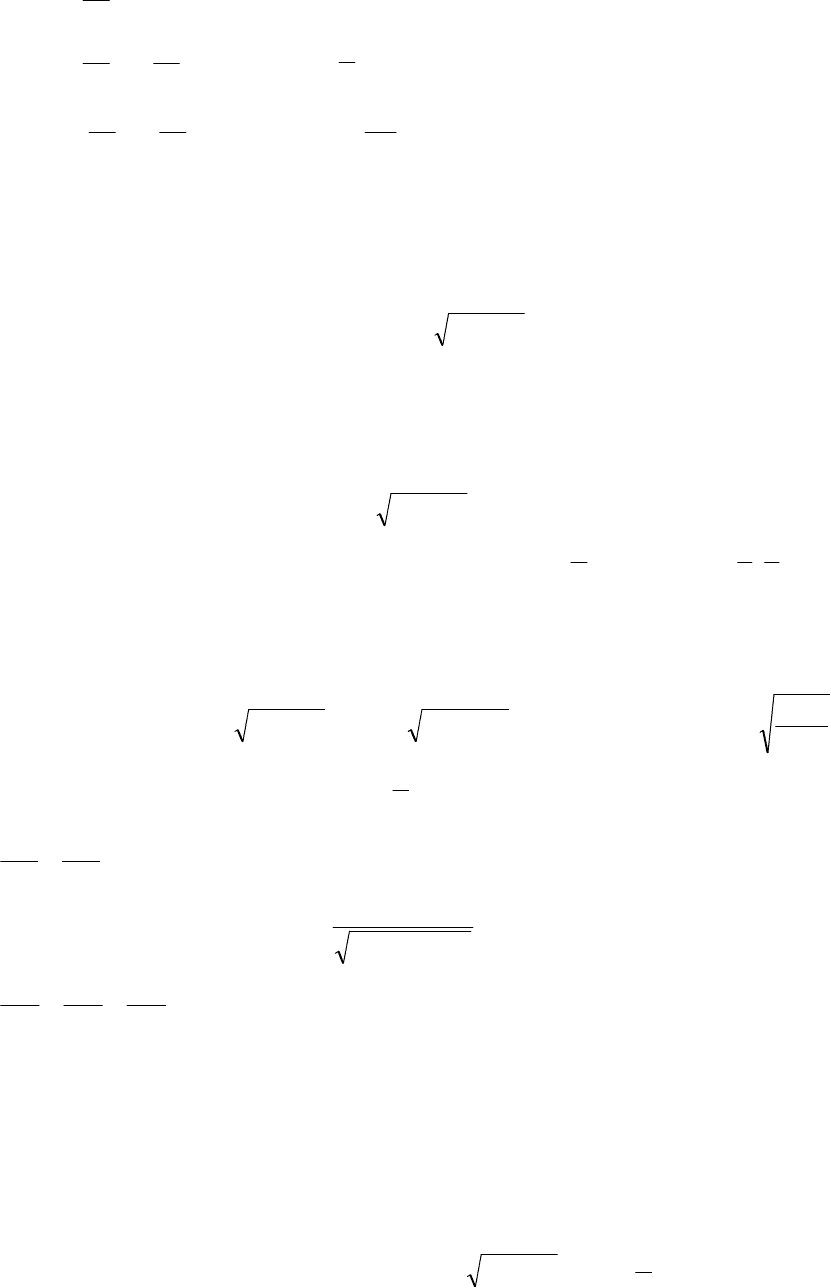
149
15.
Найти
dz
dx
, если
z
u
v
=
, где
u x v x
=
=
sin , cos
.
16.
Найти
∂
∂
z
u
, и
∂
∂
z
v
если
z arctg
x
y
=
, где
x u v y u v
=
=
sin , cos
.
17. Найти
∂
∂
u
x
, и
∂
∂
u
y
если
u v w
w
v
= +
3 3
2
2
, где
v y w x
=
=
cos , sin
.
18.
Найти производную функции
z x xy y= − −
2 2
2
в точке
P
(
;
)
1
2
в направле-
нии, составляющем с осью Ох угол в
60
o
.
19.
Найти производную функции
z x x y xy= − + +
2 2 2
2 1
в точке
M
(
;
)
1
2
по на-
правлению к точке
N
(
;
)
4
6
.
20. Найти производную функции
z x y= +
ln
2 2
в точке
P
(
;
)
1
1
в направлении
биссектрисы первого координатного угла.
21. Найти производную функции
u
xy
yz
zx
=
+
+
в точке
M
(
;
;
)
2
1
3
по направ-
лению к точке
N
(
;
;
)
5
5
15
.
22. Найти градиенты следующих функций в заданных точках:
а)
z x y xy= + −
3 3
3
,
(
;
)
2
1
; б)
z x y= −
2 2
,
(
;
)
5
3
; в)
u
xyz
=
,
(
;
;
)
1
2
3
.
23. Найти угол между градиентами функции
z
y
x
= ln
в точках
A( ; )
1
2
1
4
и
B
(
;
)
1
1
.
24.
Найти частные производные второго порядка следующих функций:
а)
z x y= +( )
2 2 2
; б)
z x y= +
ln
2 2
; в)
z xy y= +
2
2
; г)
z
x
y
=
; д)
z
x y
x
=
−
arcsin
.
25.
Показать, что функция
z arctg
x
y
=
удовлетворяет уравнению
∂
∂
∂
∂
2
2
2
2
0
z
x
z
y
+ =
.
26. Показать, что функция
u
x y z
=
+ +
1
2 2 2
удовлетворяет уравнению
∂
∂
∂
∂
∂
∂
2
2
2
2
2
2
0
u
x
u
y
u
z
+ + =
.
27. Для следующих функций найти дифференциалы второго и третьего по-
рядков:
а)
z x y=
2 3
; б)
z x y y x
=
+
cos sin
.
28.
Найти производные неявных функций:
а)
e y e x
x y
sin cos− = 0
; б)
( ) ( )x y a x y
2 2 2 2 2 2
0+ − − =
; в)
x e y e
y x2 2 2 2
0− =
.
29.
Найти первую и вторую производную неявных функций:
а)
x y e
x y
+ =
−
; б)
x
y
arctgy
−
+
=
0
; в)
ln x y arctg
y
x
2 2
0+ − =
.
30.
Найти частные производные неявных функций:

150
а)
3 4 5 60 0
2 2 2
x y z+ + − =
; б)
y
x
tg
z
c
− = 0
; в)
z ye
x
z
− = 0
.
31.
Составить уравнение нормали и касательной плоскости к каждой из
следующих поверхностей в указанной точке:
а)
2 3 4 9
2 2 2
x y z+ + =
,
M
0
1 1 1( ; ; )
−
; б)
x y z
2 2 2
0+ − =
,
M
0
3 4 5( ; ; )
;
в)
z x y= −4 9
2 2
,
M
0
11 5( ; ; )
−
; г)
x y z= +2 3
2 2
,
M
0
5 1 1( ; ; )
.
32
. Исследовать на экстремум следующие функции:
а)
z x y= − +( )1 2
2 2
; б)
z x y= − −( )1 2
2 2
; в)
z x xy y x y= + + − −
2 2
2
;
г)
z x y xy= + −
3 3
3
; д)
z x xy y x y= + + − −
2 2
3 6
.
33. Найти наибольшие и наименьшие значения функций в областях, огра-
ниченных заданными линиями:
а)
z
x
y
=
−
+
2
5
,
x
y
x
y
=
=
+
=
0
0
1
,
,
; б)
z
x
y
=
−
+
2
5
,
x
y
y
x
=
=
−
=
0
0
1
,
,
;
в)
z x y x y= − −
2
4( )
,
x
y
x
y
=
=
+
=
0
0
6
,
,
;
г)
z x y xy x y= + − − −
2 2
,
x
y
x
y
=
=
+
=
0
0
3
,
,
;
д)
z x y xy= + −
3 3
3
,
x
x
y
y
=
=
=
−
=
0
2
1
2
,
,
,
; е)
z
xy
=
,
x y
2 2
1+ =
;
ж)
z x y xy x y= + − + +
2 2
,
x
y
x
y
=
=
+
=
−
0
0
3
,
,
.
