Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

151
6. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
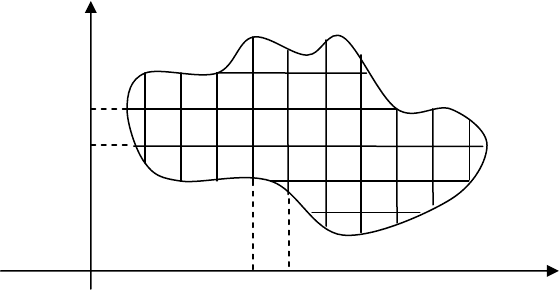
Двойной интеграл. Рассмотрим на плоскости
OXY
область (
D
), ограни-
ченную замкнутой кривой.
Разобьем область (
D
) на n частичных областей сеткой прямых, от-
стоящих друг от друга по оси х на расстояние
i
x
∆
, а по оси у – на
j
y∆
.
В каждой частичной области возьмем произвольную точку
),(
ji
yxP
и
составим интегральную сумму
∑
ji
jiji
Syxf
,
),(
где
),( yxff
=
- функция непрерывная и однозначная для всех точек области
(
D
),
ji
S
- площадь частичной области. Если при стремлении к нулю шага
разбиения области (
D
) интегральные суммы
∑
ji
jiji
Syxf
,
),(
имеют конеч-
ный предел, не зависящий от выбора точек Р, то этот предел называется
двойным интегралом от функции
),( yxf
по области (
D
) и обозначается
∫∫
)(
),(
D
dxdyyxf
Теорема. Если функция
),( yxf
непрерывна в замкнутой области (
D
),
то двойной интеграл
∫∫
)(
),(
D
dxdyyxf
существует.
Свойства двойного интегралв.
1)
Sdxdy
D
=
∫∫
)(
- площадь области (
D
)
У
Х
0
j
y
∆
i
x∆
152
2)
[
]
dxdyyxfdxdyyxfdxdyyxfyxf
DDD
∫∫∫∫∫∫
+=+
)(
2
)(
1
)(
21
),(),(),(),(
3)
∫∫∫∫
=
)()(
),(),(
DD
dxdyyxfkdxdyyxkf
(
k
=const)
4) Если
21
DDD +=
, то
dxdyyxfdxdyyxfdxdyyxf
DDD
∫∫∫∫∫∫
+=
)()()(
21
),(),(),(
Вычисление двойного интеграла.
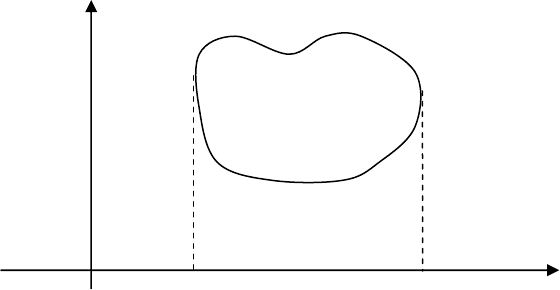
Теорема. Если функция
),( yxf
непрерывна в замкнутой области (
D
),
ограниченной линиями
,
a
x
=
bx
=
,
),(
ba
<
)(
xy
ϕ
=
,
)(
xy
ψ
=
, где
ϕ
и
ψ
-
непрерывные функции и
ψ
ϕ
≤
, тогда
( ) ( )
∫ ∫ ∫∫∫∫
=
=
b
a
b
a
x
x
x
xD
dyyxfdxdxdyyxfdxdyyxf
)(
)(
)(
)()(
,,),(
ψ
ϕ
ψ
ϕ
Пример 1. Вычислить интеграл
∫∫
−
)(
)(
D
dxdyyx
, если область (
D
) огра-
ничена линиями:
2,,0
2
===
xxyy
.
У
Х
0
)(
xy
ψ
=
)(
D
)(
xy
ϕ
=
b
a
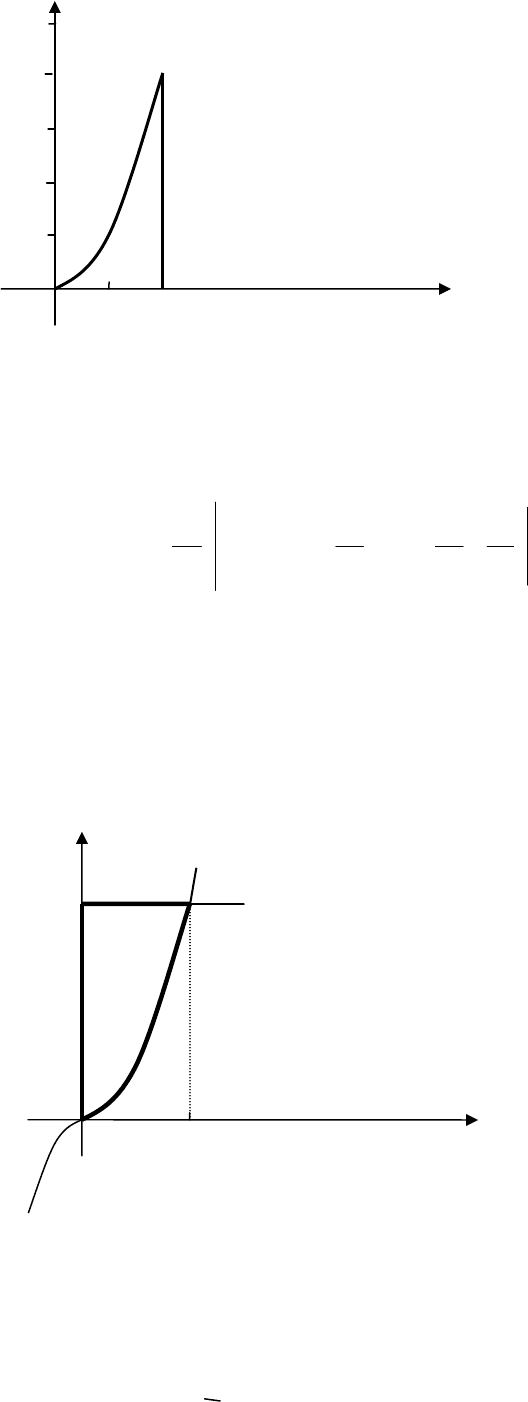
153
Имеем
20
≤
≤
x
,
2
0
xy
≤≤
, поэтому:
8,02,34
10422
)(),(
2
0
2
0
544
3
0
2
0 0
2
)(
2
2
=−=
−=
−=
−=−=
∫∫ ∫∫∫
xx
dx
x
x
y
xydyyxdxdxdyyxf
x
x
D
Теорема. Если функция
),(
yxf
непрерывная в замкнутой области (
D
), ог-
раниченной линиями
)(,
dcdycy
<
=
=
,
)(
yx
Φ
=
,
(
)
)()()( yyyx Ψ≤ΦΨ=
, то
∫∫
)(
),(
D
dxdyyxf
=
∫ ∫
Ψ
Φ
d
c
y
y
dxyxfdy
)(
)(
),(
Пример 2. Вычислить интеграл
∫∫
)(D
xydxdy
, если область (
D
) ограни-
чена линиями
3
xy =
,
8
=
y
,
0
=
x
. Поменять порядок интегрирования
0
у
8
8
=
y
0
=
x
2
0
у
4
2
х
2
xy =
х
3
xy =
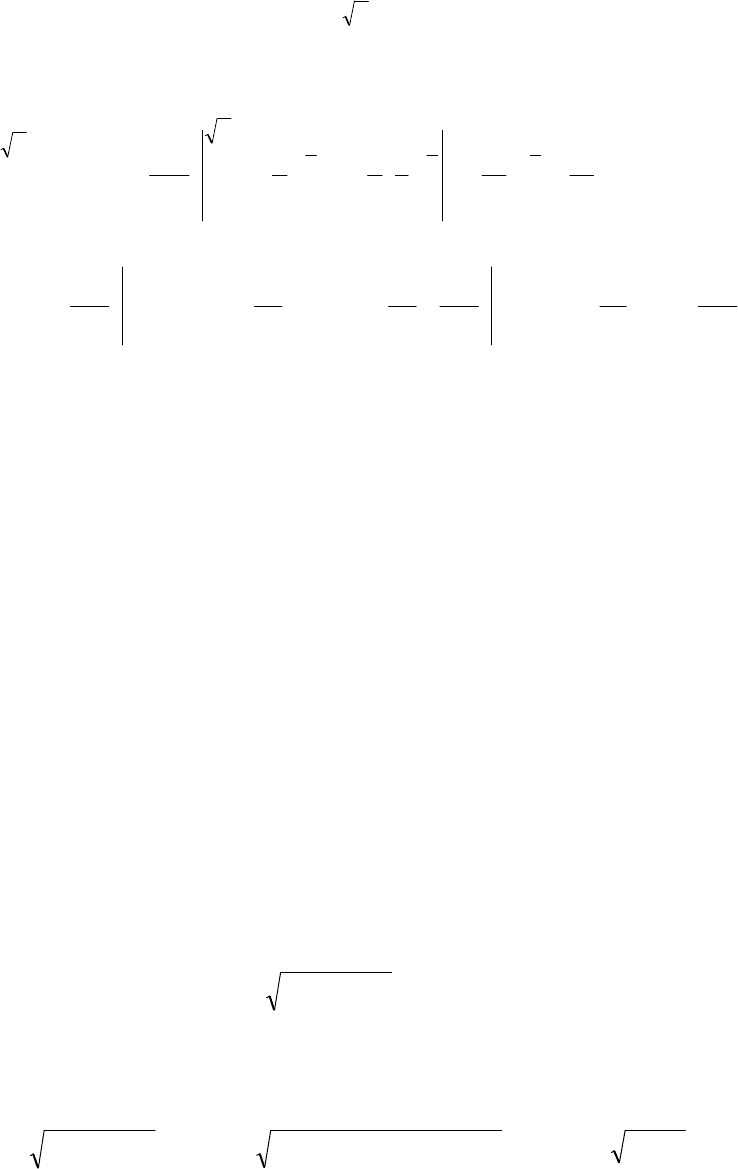
154
Имеем
∫ ∫ ∫ ∫∫∫
==
2
0
8 8
0 0)(
3
3
x
y
D
xydxdydyxydxdydxxy
482
16
3
8
16
3
8
3
2
1
2
1
2
8
3
8
8
0
8
0
3
8
3
5
0
8
0 0
8
0
2
3
3
=⋅=⋅=⋅==
=
∫∫ ∫ ∫
ydyy
yx
dyxydydy
y
y
, а также
481664
16
256
64
16
2
416
822
32
2
32
2
8
2
0
82
2
0
8 2
0
2
0
7
8
2
3
3
=−=−=−⋅=
⋅
−⋅=
−=
=
∫ ∫ ∫ ∫
xx
dx
x
x
xy
dxxydydx
x
x
Двойной интеграл в полярных координатах.
При переходе от декартовых координат к полярным координатам
имеет место формула:
∫∫
)(
),(
D
dxdyyxf
=
∫∫
*)(
)sin,cos(
D
drrdrrf
ϕϕϕ
где
*)(D
- область в полярной системе координат, соответствующая
области (
D
) в декартовой системе координат. Пусть область
*)(D
задается
следующими неравенствами:
)()(,
2
1
ϕϕβϕα
rrr ≤≤≤≤
. Тогда будем иметь:
rdrrrfddrrdrrf
r
rD
)sin,cos()sin,cos(
)(
)(*)(
2
1
ϕϕϕϕϕϕ
β
α
ϕ
ϕ
∫ ∫∫∫
=
.
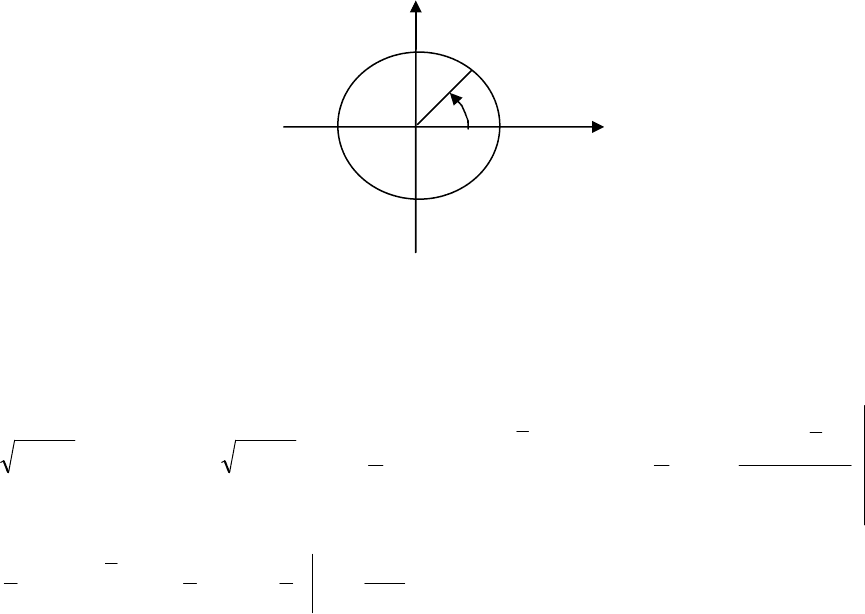
Пример 3. Вычислить
dxdyyx
D
∫∫
−−
)(
22
4
, где (
D
) – круг
4
22
≤+ yx
.
Применив формулу перехода к полярным координатам, получим:
drrdrdrrdrrdxdyyx
DDD
ϕϕϕϕ
∫∫∫∫∫∫
−=−−=−−
)(
2
*)(
2222
)(
22
4sincos44
.
Область (
D
) в полярной системе координат определяется неравенст-
вами
π
ϕ
20
≤
≤
,
20
≤
≤
r
.
155
Заметим, что область (
D
) – круг – преобразуется в область
*)(
D
-
прямоугольник. Имеем:
( ) ( )
( )
=
⋅−
−=−−−=−=−
∫∫ ∫∫∫∫∫
2
0
2
0
2
3
2
2
2
1
2
0
2
0
2
2
0
2
2
0*)(
2
3
24
2
1
44
2
1
44
πππ
ϕϕϕϕ
r
drdrdrdrrddrrdr
D
3
16
3
8
3
8
40
3
1
2
0
2
0
2
0
2
3
π
ϕϕϕ
π
ππ
===
−−=
∫∫
dd
.
Тройной интеграл. Пусть в замкнутой области (V) пространства OXYZ за-
дана непрерывная функция
),,( zyxff
=
. Разбив область (V) плоскостями,
параллельными координатным плоскостям, на конечное число элементар-
ных частей, объемы которых обозначим
ijk
V
и выбрав значение функции f
в некоторой точке этого элементарного объема
),,(
kji
zyxf
, составим инте-
гральную сумму
ijk
kji
kji
Vzyxf ),,(
,,
∑
Если при стремлении к нулю элементарных объемов
ijk
V
разбиения
области (V) интегральные суммы имеют конечный предел, не зависящий от
выбора точек внутри
ijk
V
, то этот предел называется тройным интегралом
от функции
),,(
kji
zyxf
по области (V) и обозначается
∫∫∫
)(
),,(
V
dxdydzzyxf
Теорема существования и свойства тройного интеграла аналогичны
двойному интегралу.
Вычисление тройного интеграла.
Теорема. Если функция
),,( zyxf
непрерывна в замкнутой области
),(),(:)(
21
yxzzyxzV ≤≤
,
)()(
21
xyyxy ≤≤
,
bxa
≤
≤
, тогда
0
-
2
2
r
ϕ
y
2
-
2
x
156
∫∫∫ ∫ ∫ ∫
=
)(
)(
)(
),(
),(
2
1
2
1
),,(),,(
V
b
a
xy
xy
yxz
yxz
dzzyxfdydxdxdydzzyxf
Замечание. Как и в случае двойного интеграла возможен и другой
порядок интегрирования.
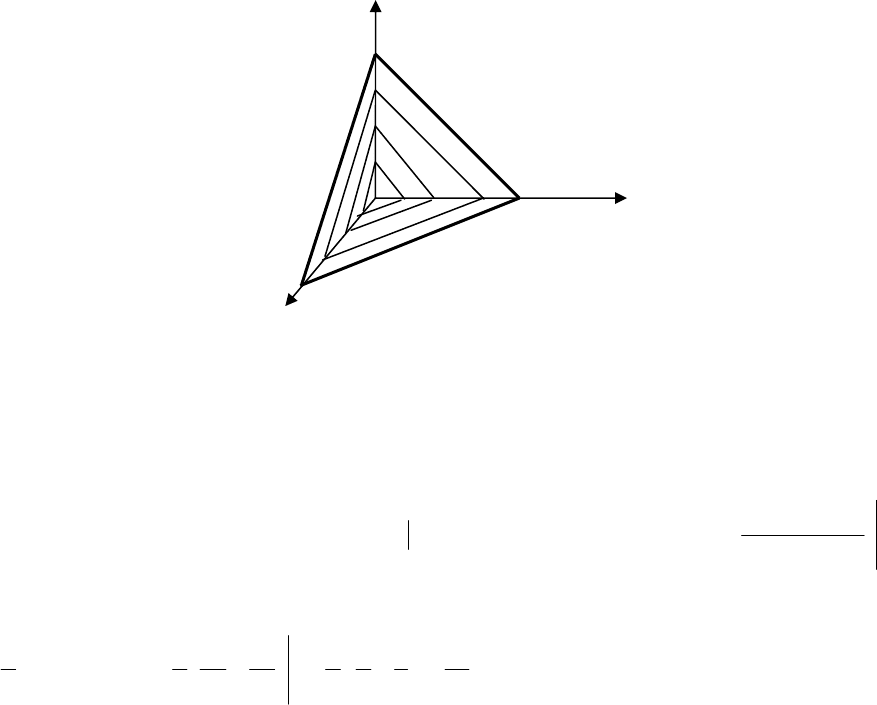
Пример 4. Вычислить интеграл
∫∫∫
)(
V
dxdydzx
, где
≥≥≥
≤++
0;0;0
1
:)(
zyx
zyx
V
Рис. 1.
Область (V) изображена на Рис. 1.
Имеем:
=
−
−−
=−−===
−
−
−−
−
−−
−
∫ ∫ ∫∫ ∫ ∫ ∫ ∫∫∫∫
x
x
yx
x
yx
x
V
yxx
dxdyyxxdxxzdydxdzxdydxdxdydzx
1
0
1
0
1
0
1
0
2
1
0
1
0
1
0
1
0
1
0
1
0)(
2
)1(
)1()(
12
1
3
1
2
1
2
1
322
1
)1(
2
1
1
0
32
1
0
=
−=
−=−−−=
∫
xx
dxxx
.
Пример 5. Вычислить объем тела, ограниченного поверхностями
22
2yxz +=
;
0
=
z
;
4
=
x
;
2
=
y
;
0
=
x
;
0
=
y
.
0
1
1
1
y
z
x+y+z=1
x+y=1

157
Объем тела
( )
∫∫∫ ∫ ∫ ∫ ∫ ∫∫ ∫
+
+
=+====
)(
4
0
2
0
2
0
4
0
2
0
22
4
0
2
0
2
0
22
22
2)(
V
yx
yx
dyyxdxzdydxdzdydxdxdydzV
∫∫
=⋅+⋅=
+=
+=
+=
4
0
3
4
0
3
2
2
0
3
2
4
0
644
3
16
4
3
2
3
16
3
2
3
16
2
3
2
x
x
dxx
y
yxdx
Криволинейные интегралы. Рассмотрим на примерах вычисление
криволинейных интегралов:
Пример 6.
∫
−+=
L
dyyxxydxJ )(
, где
L
- кривая
3
xy =
, пробегаемая от
точки
)0;0(A
, до точки
)8;2(B
. Имеем
dxxdy
2
3=
, отсюда
( ) ( )
=⋅−+⋅=
−+=−+=−+⋅=
∫ ∫
64
2
1
5
32
16
4
3
6
3
54
3
333
2
0
6
5
4
2
0
2
0
543233
x
x
xdxxxxdxxxxdxxxJ
6,13324,612
−
=
−
+
=
.
Пример 7.
∫
++=
L
xdydxxyJ )(
, где
L
- кривая
+=
+=
tty
ttx
2
3
2
, пробегаемая
от точки
)3;2(A
, до точки
)12;6(B
. Данным точкам соответствуют значения
2;1
21
== tt
.
Имеем
(
)
dttdydttdx 23,)12(
2
+=+=
, отсюда
( )
( )
( )( ) ( )
=
+++=+++=+++++++=
∫ ∫
2
1
23
45
2
1
2
1
2342223
2
5
3
9
4
6
596523122
tt
ttdtttttdttttdttttttJ
82
2
5
3
2
3
1)10242432( =
+++−+++=
.
z
y
2
0
4
x
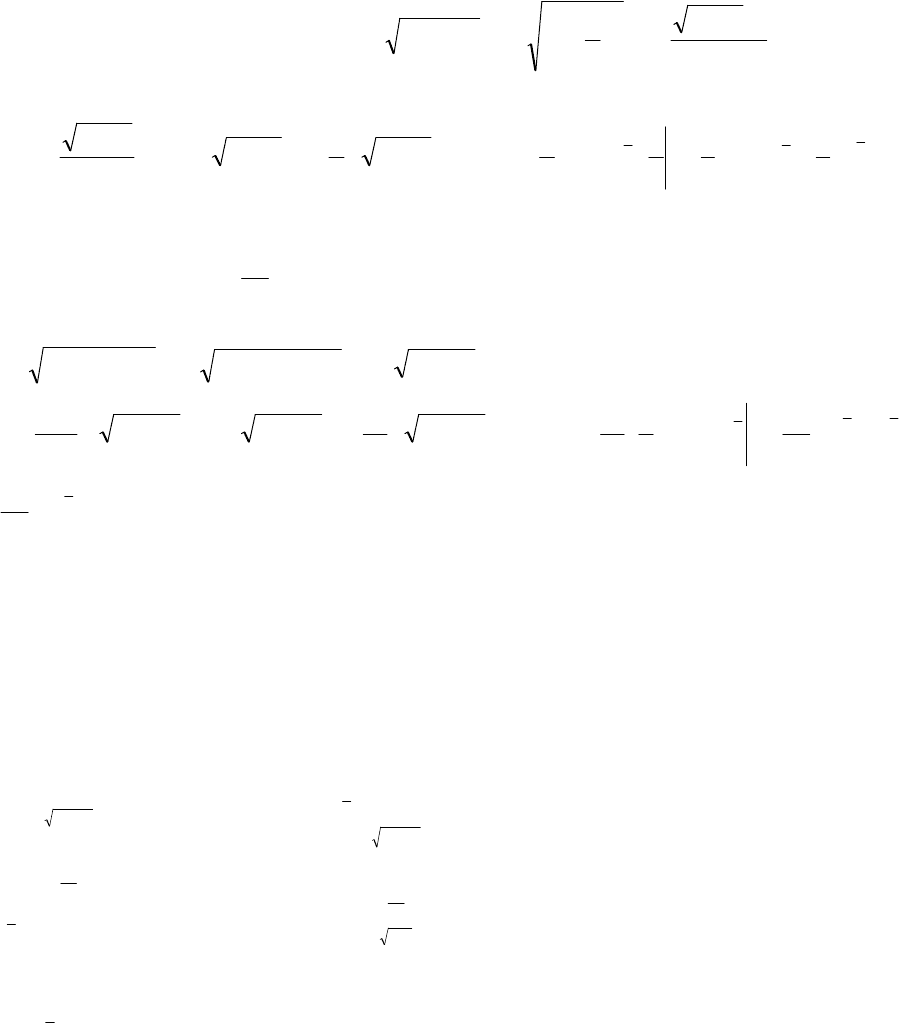
158
Пример 8.
∫
=
L
dsxJ
2
, где
L
- кривая
xy
ln
=
, пробегаемая от точки
)0;1(
A
, до точки
)1;(
eB
. Имеем
( )
x
dxx
dx
x
dxyds
x
2
2
2
11
11
+
=
+=
′
+=
,
ex
≤
≤
1
.
Поэтому
( ) ( )
2
3
2
3
2
1
1
2
3
22
1
2
1
2
2
2
2
3
1
1
3
1
3
2
1
2
1
)1(1
2
1
1
1
⋅−+=⋅+=++=+=
+
=
∫ ∫∫
exxdxdxxxdx
x
x
xJ
e
e
ee
.
Пример 9.
∫
=
L
ds
x
y
J
3
2
, где
L
- кривая
≤≤
=
=
=
10
3
2
t
ty
tx
y
. Имеем
( ) ( )
dtttdtttdtyxds
tt
2222
22
94)3()2( +=+=
′
+
′
=
. Поэтому
(
)
( )
( ) ( )
∫∫∫
=−=+⋅=++=+=+⋅=
1
0
2
3
2
3
1
0
2
3
222
1
0
2
1
0
2
3
2
2
3
)413(
27
1
94
3
2
18
1
9494
18
1
9494 ttdtdtttdttt
t
t
J
−= 813
27
1
2
3
.
Задачи для самостоятельного решения.
Изменить порядок интегрирования. Область интегрирования изобразить на
чертеже.
1.
dx f x y dy
x
x
0
1
2
3
2
∫ ∫
−
( , )
.
2.
dx f x y dy
x
x
0
4
3
4
25
2
∫ ∫
−
( , )
.
3.
dy f x y dx
y
y
0
3
2
2
3
2
∫ ∫
+
( , )
.
4.
dx f x y dy
x
( , )
0
1
1
2
∫∫
.
5.
dx f x y dy
x
x
−
+
∫ ∫
1
0
2
3
2
( , )
.
6.
dy f x y dx
y
y
0
1
2
3
2
∫ ∫
−
( , )
.
7.
dx f x y dy
x
0
1
1
1
2
∫ ∫
−
+
( , )
.
8.
dx f x y dy
x
x
−
−
∫ ∫
3
2
0
2
3
2
( , )
.
9.
dy f x y dx
y
y
0
4
3
4
25
2
∫ ∫
−
( , )
.
10.
dy f x y dx
y
y
0
4
16
3
∫ ∫
( , )
.
159
Вычислить двойные интегралы по соответствующим областям.
11.
( ) ,x y dxdy
D
+
∫∫
2
где (D)-область, ограниченная линиями
x
x
y
y
=
=
=
=
0
2
0
3
,
,
,
.
12. x ydxdy
D
2
∫∫
,
где (D)-область, ограниченная линиями
y
x
y
x
=
=
=
2
0
1
,
,
.
13. ( ) ,x y dxdy
D
2
−
∫∫
где (D)-область, ограниченная линиями
y x y x= = =
3
0 2, , .
14. xydxdy
D
∫∫
,
где (D)-область, ограниченная линиями
y x y x= = =, , .0 4
15. ( ) ,y x dxdy
D
−
∫∫
2
где (D)-область, ограниченная линиями
y
y
x
x
=
=
=
2
0
,
,
.
16. xy dxdy
D
2
∫∫
,
где (D)-область, ограниченная линиями
y x y x= = =
3
8 0, , .
Перейти к полярным координатам, вычислить.
17.
xydxdy
D
∫∫
,
где (D)-область, ограниченная линией
x y x y
2 2
1 0 0+ = ≥ ≥, , .
18. ydxdy
D
∫∫
,
где (D)-область, ограниченная линиями
x y y y
2 2
4 1 1+ = = ≥, ;( ).
19. x dxdy
D
2
∫∫
,
где (D)-область, ограниченная линиями
x y x x
2 2
9 0 0+ = = ≥, ;( ).
20. xdxdy
D
∫∫
,
где (D)-область, ограниченная линией
x y x
2 2
2+ ≤ .
21. Вычислить площади фигур, ограниченных линиями.
1.
xy
y
x
x
=
=
=
4
4
,
,
.
2.
y x y x y= = =
2 2
4 4, , .
3.
y x y x x x= = = = −
2 2
4 2 2, , , .
4.
y x x y
2
4 3 0= + + =, .
5.
y x y x= − =
2
2, .
6.
y x x y y
=
−
=
=
−
ln , , .1 1
7.
( ) .x y x
2 2 3 2
+ =
8.
( ) .x y x y
2 2 3 2 2
2+ = +
9.
( ) .x y x y
2 2 5 3
+ =
10. ( ) .x y xy
2 2 2
+ =
11.
ρ
ϕ
=
−
2
cos
.
12.
ρ
ϕ
=
sin .
13.
ρ
ϕ
=
cos
.
2
22. Вычислить объемы тел, ограниченных поверхностями:
1.
z x y x y x z y= + + = = = =
2 2
4 0 0 0; ; ; ; .
2.
x y z y x x z y+ + = = = = =3 1 0 0
2
; ; ; ; .
3.
z x y y x y z= + = = =
2 2 2
1 0; ; ; .
4.
z x y x y z= − − + = =1 1 1
2 2 2 2
; ; .
5.
z x y x y z= = + = =
2
0 1 0; ; ; .
6.
z y x x z= − = = =4 0 2 0
2
; ; ; .
7.
x y x y z z
2 2
4 4 0+ = + + = =; ; .
8.
x y x x z z
2 2
2 6 0+ = + = =; ; .
9.
z x y y x y x z x= + = = = =
2 2
2 2 0 1; ; ; ; .
10. x y z z
2 2 2
4 1+ + = ≥; .
23. Вычислить следующие криволинейные интегралы по соответствующим
кривым:
160
1.
xdy ydx
L
−
∫
( )
,
где (L)- есть верхняя половина эллипса
x a t y b t
=
=
cos , sin ,
пробегаемая против хода часовой стрелки.
2.
( ) ( ) ,
( )
x y dx x y dy
L
2
− + +
∫
где (L)- есть треугольник с вершинами в точках О(0;0),
А(1;0), В(0;1), пробегаемый против хода часовой стрелки.
3.
2xdy ydx
L
+
∫
( )
,
где (L)- есть дуга параболы
y x
2
=
от точки А(1;1) до точки
В(4;2).
4.
y
y
dx
x
y
dx
L
2
2
1+
−
∫
( )
,
где (L)- есть отрезок прямой, соединяющей точку А(1;2) с
точкой В(2;4).
5.
2 3
3 2 2
xy dx x y dy
L
+
∫
( )
,
вдоль любой кривой, соединяющей точки А(1;2) и В(2;4).
6.
ydx xdy
x y
L
−
+
∫
2 2
( )
,
где (L)- есть окружность
x R t y R t
=
=
cos , sin ,
пробегаемая по ходу
часовой стрелки.
7.
( ) ( ) ,
( )
x y dx y x dy
L
2 2
− + −
∫
вдоль любой кривой, соединяющей точки А(0;0) и
В(3;4).
8.
( ) ( ) ,
( )
x y dx x y dy
L
− + +
∫
где (L)- есть окружность
x R t y R t
=
=
cos , sin ,
пробегаемая
против хода часовой стрелки.
9.
ydx
x
y
dy
L
+
∫
( )
,
где (L)- есть дуга кривой
y e
x
=
−
от точки А(0;1) до точки В(-1;е).
10. ( ) ( ) ,
( )
3 1 2
2 3
x y dx x dy
L
+ + −
∫
где (L)- дуга кубической параболы, соединяющей
точки А(1;1) и В(2;8).
11. xds
L( )
,
∫
где (L)- есть дуга кривой
y
x
=
2
2
,
соединяющей точки А(1;0,5) и В(2;2).
12. yds
L( )
,
∫
где (L)- есть дуга кривой
y
x
=
3
3
,
соединяющей точки А(0;0) и В(3;9).
13.
y
x
ds
L
2
3
( )
,
∫
где (L)- есть дуга кривой
y
x
=
4
4
,
соединяющей точки А
( ; )1
1
4
и
В(2;4).
14. y ds
L
2
( )
,
∫
где (L)- есть дуга кривой
y e
x
= ,
соединяющей точки А(0;1) и В
(
;
)
1
e
.
15. xyds
L( )
,
∫
где (L)- есть дуга кривой
x t
y t
t
=
=
≤ ≤
2
2
0
2
sin ,
cos ,
.
π
