Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

161
7. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Обыкновенным дифференциальным уравнением называется уравнение
относительно неизвестной функции и ее производных различного порядка
0) ..., , , , ,(
)(
=
′′′
n
yyyyxF
.
Порядком дифференциального уравнения называется максимальный порядок
производной, входящей в него.
Решением дифференциального уравнения называется функция, которая обра-
щает это дифференциальное уравнение в тождество.
Процесс нахождения решения данного дифференциального уравнения назы-
вается интегрированием этого уравнения.
Уравнение
,
связывающее между собой независимую переменную, искомую (неизвест-
ную) функцию
, и ее производную называется дифференциаль-
ным уравнением первого порядка.
Если это уравнение можно записать в виде
,
то говорят, что оно разрешимо относительно производной.
Решением (или интегралом) дифференциального уравнения первого порядка
называется любая функция
которая при подстановке в это уравне-
ние обращает его в тождество. График функции
в этом случае на-
зывается интегральной кривой.
Задача отыскания решения дифференциального уравнения первого порядка,
удовлетворяющего заданному начальному условию
,
называется задачей Коши.
Геометрически это равносильно следующему: требуется найти интегральную
кривую уравнения
, проходящую через точку .
Общим решением уравнения
называется такая функция
,
где C - произвольная постоянная, что:
1) при любом конкретном значении С она является решением этого
уравнения;
2) для любого допустимого начального условия
, в окрестно-
сти которого существует решение, найдется такое значение постоянной
, что .
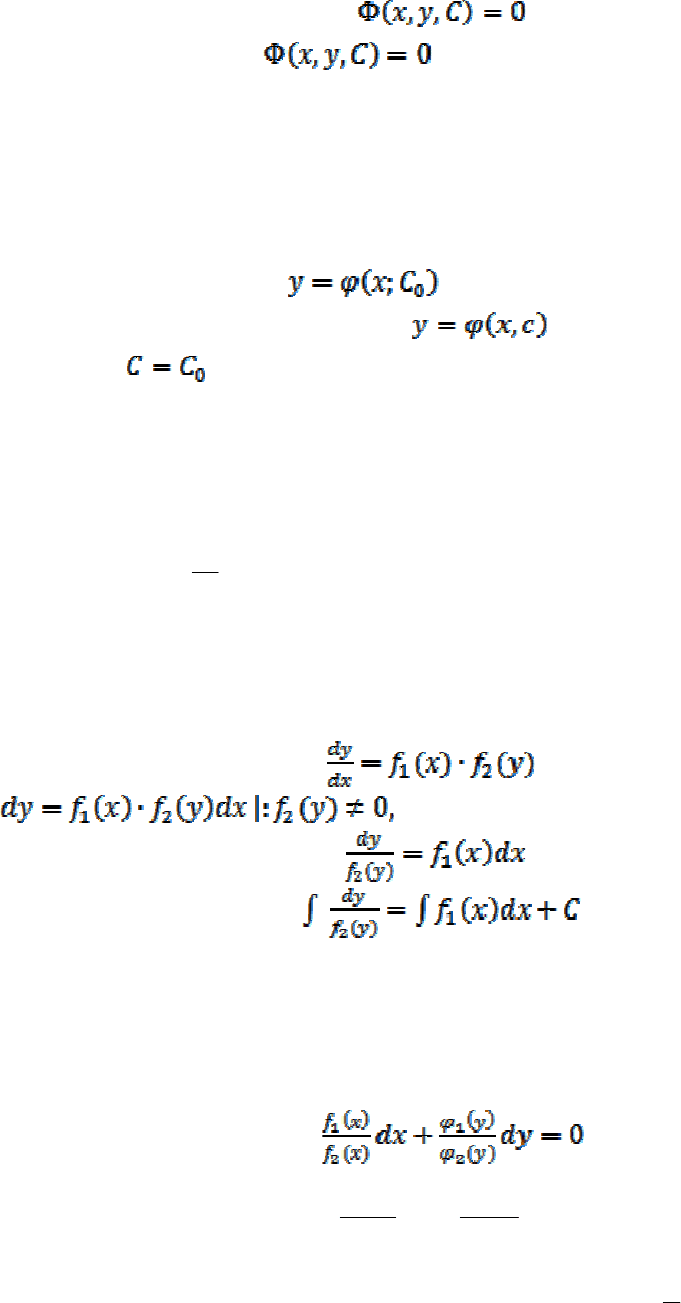
162
В некоторых случаях общее решение дифференциального уравнения прихо-
дится записывать в неявном виде:
.
Тогда соотношение
называется общим интегралом этого
уравнения.
Геометрически общий интеграл представляет собой семейство интегральных
кривых на плоскости Оху.
Частным решением дифференциального уравнения первого порядка называ-
ется функция
,
получаемая из общего решения
при конкретном значении по-
стоянной
.
Уравнения с разделяющимися переменными. Уравнение вида
)()(
21
yfxfy
⋅
=
′
,
где
)(
1
xf
и
)(
2
yf
− непрерывные функции, называется дифференциальным
уравнением с разделяющимися переменными.
Для отыскания решения такого дифференциального уравнения нужно:
1)
y
′
заменить
;
dx
dy
2) разделить переменные (преобразовать уравнение таким образом, чтобы в
левой части содержались функция и дифференциал, например, переменной
x
,
а в правой – функция и дифференциал, например, переменной
y
).
)()(
21
yfxfy
⋅
=
′
,
,
.
Дифференциальное уравнение с разделяющимися переменными может быть
задано в следующем виде:
0)()()()(
2211
=
⋅
+
⋅
dyyxfdxyxf
ϕ
ϕ
Разделим обе части уравнения на
0)(
1
≠
y
ϕ
и
0)(
2
≠
xf
, получим
,
∫ ∫
=+ Сdy
y
y
dx
xf
xf
)(
)(
)(
)(
1
2
2
1
ϕ
ϕ
.
Пример 1. Решить дифференциальное уравнение
x
y
y =
′
.
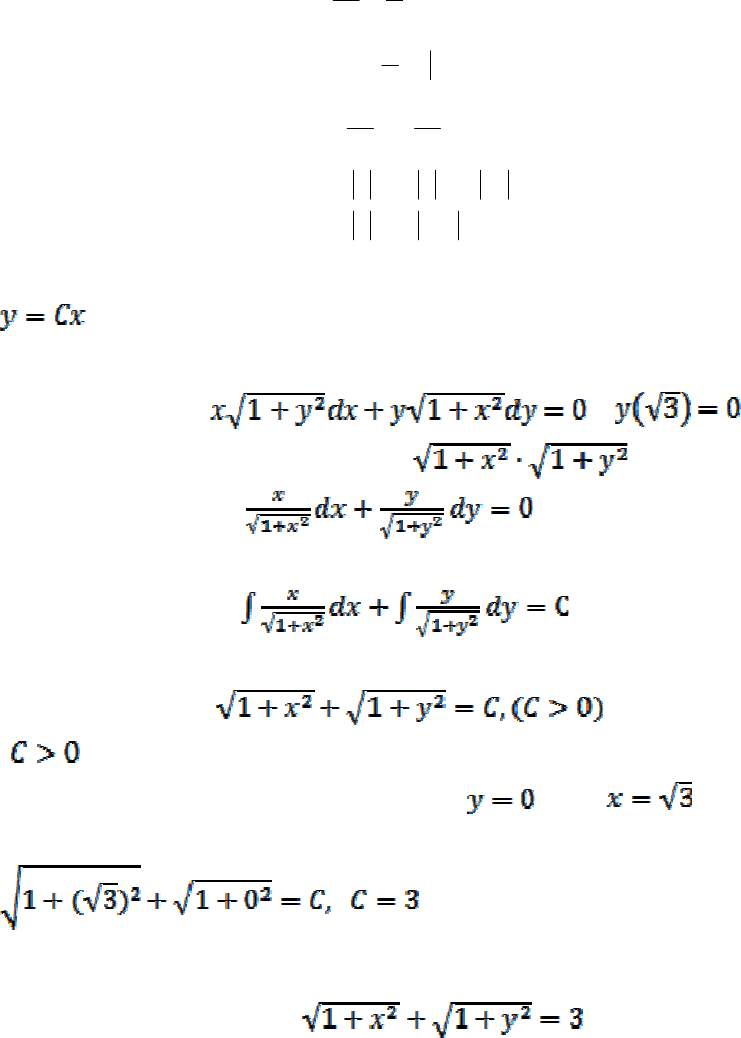
163
,0:
,
≠=
=
ydx
x
y
dx
x
y
dx
dy
.
,lnln
,lnlnln
,
1
1
Cxy
xCy
Cxy
x
dx
y
dy
=
=
+=
=
∫ ∫
- общее решение уравнения.
Пример2. Решить задачу Коши:
, .
Разделим обе части уравнения на
. Получим
.
Интегрируя обе части этого уравнения, получим общий интеграл:
.
Отсюда
.
(
, так как рассматриваются только арифметические значения корня.)
Частное решение получим из условия
при .
Подставляя эти значения х и у в общий интеграл, получим
и частным решением будет
.
Однородные дифференциальные уравнения. Функция
) ;( yxF
называется од-
нородной степени (порядка)
k , если при любом
t
выполняется тождество
). ;() ;( yxFttytxF
k
=
) ;() ;()2(2) ;(
,2) ;(
111
1
yxFyxFtyxttytxtytxF
yxyxF
⇒⋅⋅=+⋅=+=
+=
- однородная функция первой степени.
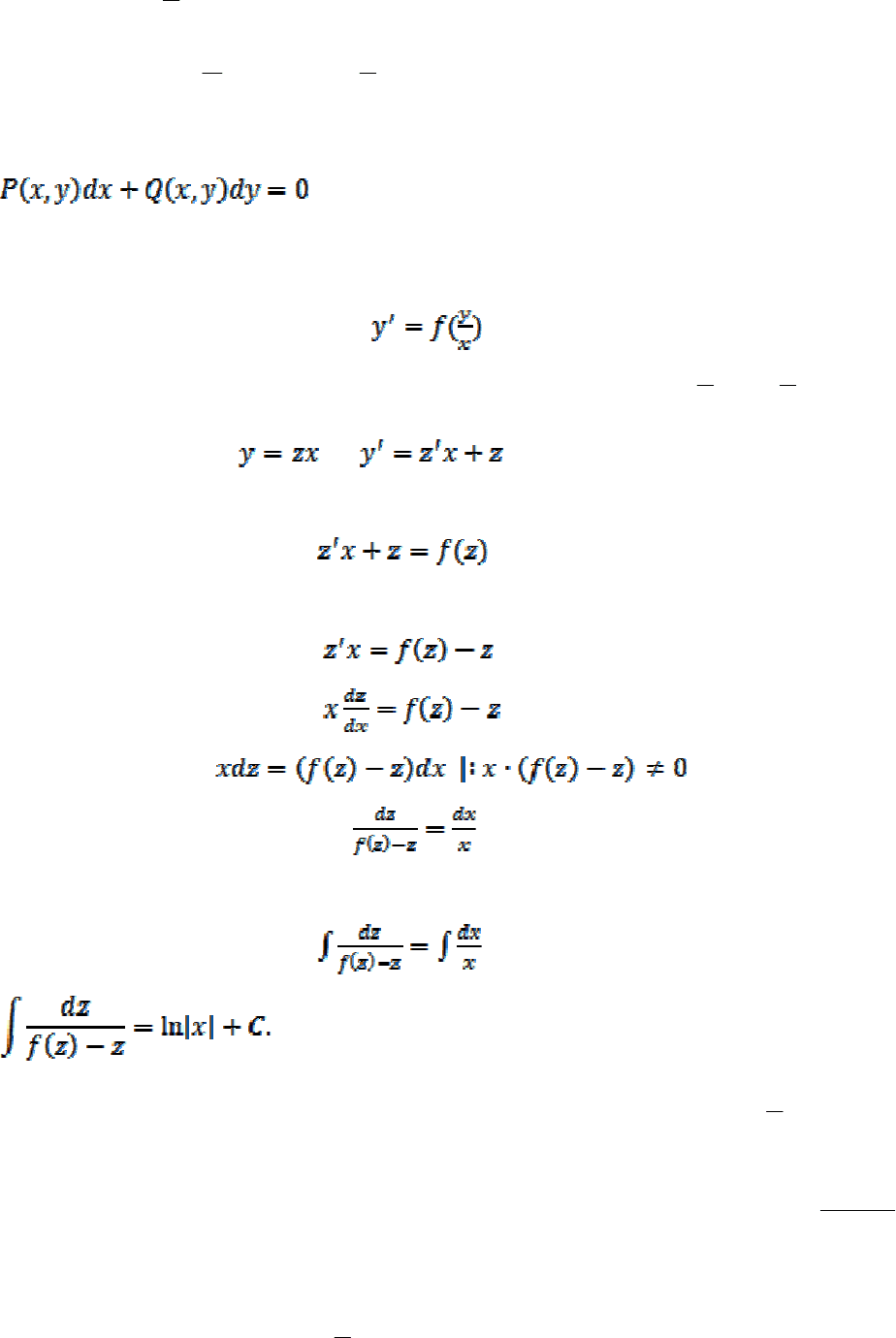
164
) ;() ;(sinsin)() ;(
sin) ;(
22
2222
2
2
2
yxFyxFt
y
x
xt
ty
tx
txtytxF
y
x
xyxF
⇒=
⋅⋅=⋅=
=
- однородная функция второй степени.
Дифференциальное уравнение I порядка
называется однородным, если
) ;( yxP
и
−
) ;( yxQ
однородные функции одной и
той же степени
.k
Это уравнение может быть приведено к виду
.
Способ решения. Введем вспомогательную функцию
==
x
y
z
x
y
xz , )(
, тогда
, ,
подставляя в уравнение, получим
.
Откуда
,
,
,
.
Интегрируя, получим
,
Решив полученное уравнение относительно
,
z
делаем замену
x
y
z =
и выра-
жаем функцию
.
y
Пример 3. Найти общее решение дифференциального уравнения
xy
yx
y
2
22
+
=
′
Функции, стоящие в числителе и знаменателе, однородные II степени, данное
уравнение является однородным.
Введем новую функцию
. , , zxzyzxy
x
y
z +
′
=
′
==
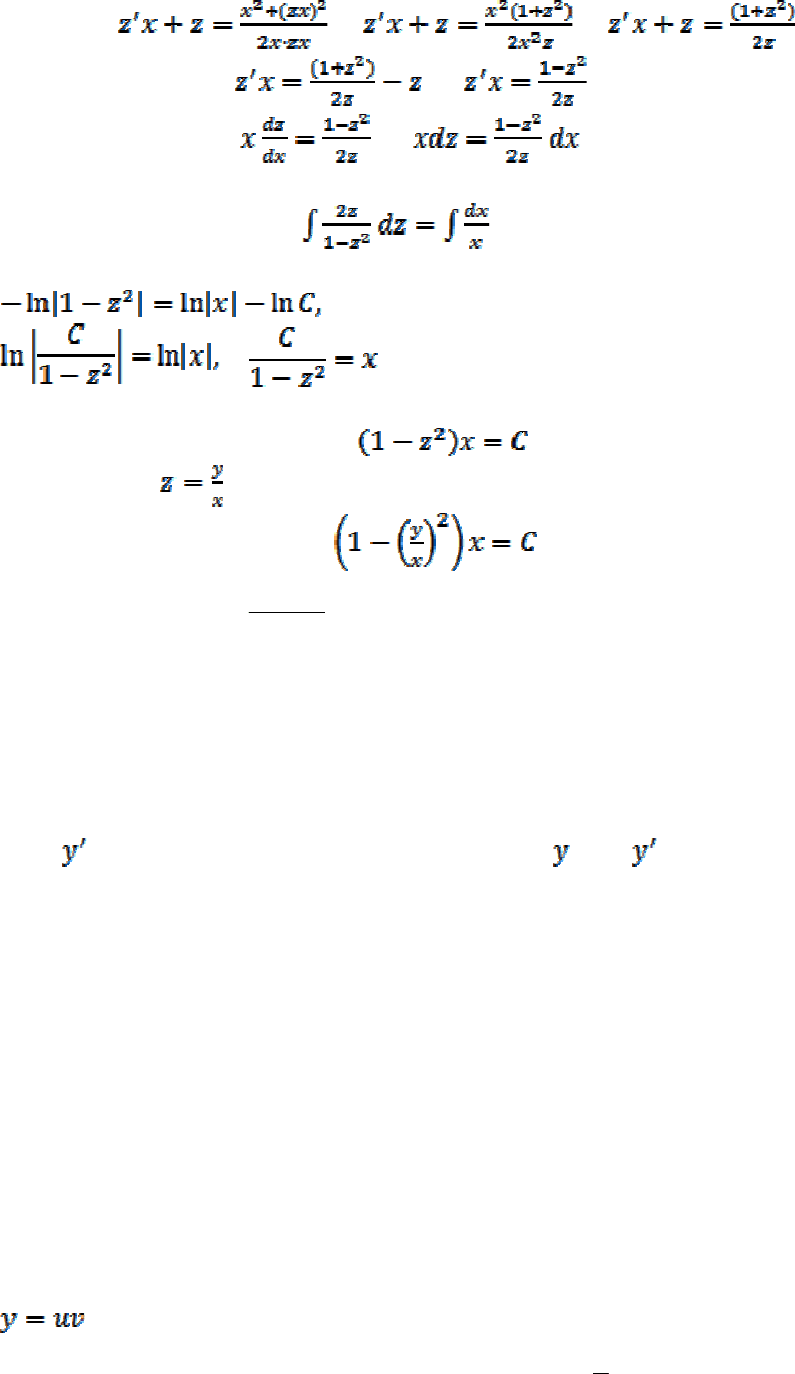
165
Получим
, , ,
, ,
, .
Разделяя переменные и интегрируя, получим
.
Откуда
или
.
Подставляя
, получим
,
С
x
yx
=
−
22
- общее решение уравнения.
Линейные уравнения первого порядка. Линейным дифференциальным уравне-
нием I порядка называется уравнение вида
)()( xfyxpy
=
+
′
.
Способ решения. Если
,0)(
≠
xf
то решение уравнения будем искать в виде
v
u
y
⋅
=
(где
u
и
−
v
функции, зависящие от
x
т. е.
)( ),( xvvxuu
=
=
). Нахо-
дим
и подставляем в уравнение значения и :
(*) ),())((
),()(
,
xfvxpvuvu
xfuvxpvuvu
vuvuy
=⋅+
′
⋅+
′
=⋅+
′
+
′
′
+
′
=
′
Выберем функцию
v
такую, чтобы выражение в скобках
0)(
=
⋅
+
′
vxpv
. Тогда
уравнение (*) сведется к системе двух дифференциальных уравнений.
=
′
=⋅+
′
)2( )(
)1( 0)(
xfvu
vxpv
Решим уравнение (1) системы:
0)(
=
⋅
+
′
vxpv
,
Имеем линейное однородное дифференциальное уравнение I порядка, кото-
рое является уравнением с разделяющимися переменными. Находим из этого
уравнения функцию v, подставляем ее значение во второе уравнение и опре-
деляем функцию u. Запишем общее решение исходного уравнения в виде
.
Пример 4. Найти общее решение уравнения
.
2
xy
x
y =+
′
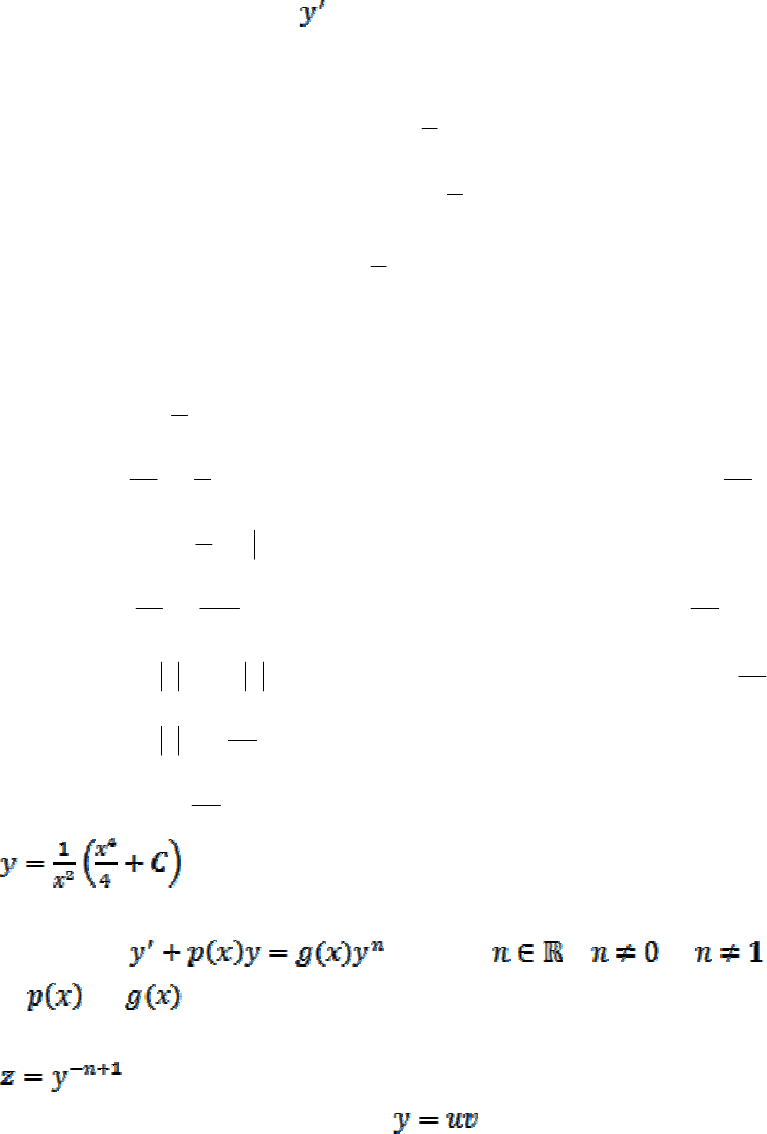
166
Будем искать решение в виде:
,
,
vuvuy
uv
y
′
+
′
=
′
=
Подставляя значения y
в уравнение, группируя по переменной u, перей-
дем к системе двух дифференциальных уравнений, каждое из которых явля-
ется уравнением с разделяющимися переменными, и решим их.
=
′
=+
′
=
+
′
⋅+
′
=+
′
+
′
(2) .
(1) ,0
2
,
2
,
2
xvu
v
x
v
xv
x
vuvu
xuv
x
vuvu
Решим (1) уравнение системы: Решим (2) уравнение системы:
.
x
1
v
,
x
1
lnvln
,
4
,x-2lnvln
, ,
x
2dx
-
v
dv
, v,:vdx
x
2
-dv
,
1
v,
x
2
-
dx
dv
, 0,v
x
2
v
2
2
4
33
3
2
=
=
+==
=⇒==
=
′
=
=⋅
′
=
=
′
=+
′
∫ ∫
C
x
u
dxxdux
dx
du
xu
x
x
u
xvu
- общее решение уравнения.
Уравнения Бернулли. Уравнение вида
, где , , ,
а
и - непрерывные функции, называется уравнением Бернулли.
Это уравнение приводится к линейному уравнению с помощью подстановки
. Уравнение Бернулли можно, не сводя к линейному, проинтегри-
ровать с помощью подстановки
(т.е. методом Бернулли) или приме-
нив метод вариации произвольной постоянной (метод Лагранжа).
Уравнения второго порядка, допускающие понижение порядка. Рассмотрим
отдельные примеры.
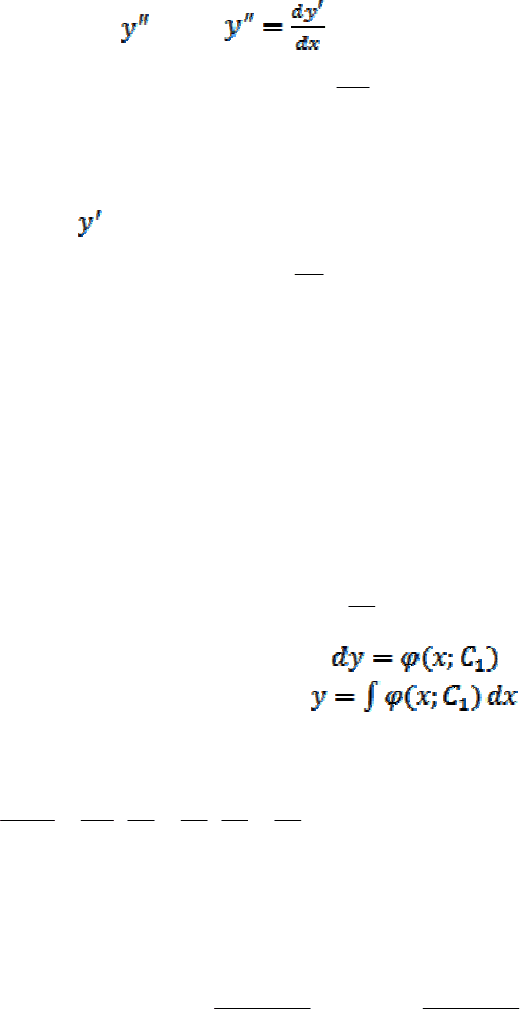
167
1) Уравнение вида
0) ;(
=
′
′
yxF
или это уравнение может быть записано в виде
)(xfy
=
′
′
. В данном уравнении не содержится
y
и
y
′
, поэтому решить его
можно с помощью двукратного интегрирования.
Пример 5. Найти общее решение уравнения
0sin
=
−
′
′
xy
.
Представим
как , получим
,cos
,sin
,sin
1
Cxy
xdxyd
x
dx
yd
+−=
′
=
′
=
′
∫ ∫
Заменяем
на отношение дифференциалов
.sin
,)cos(
,cos
21
1
1
CxCxy
dxCxdy
Cx
dx
dy
++−=
+−=
+−=
∫ ∫
2) Уравнение вида
0) ; ;(
=
′
′
′
yyxF
не содержит переменную
y
. С помощью
подстановки
)(xzy
=
′
преобразуется в дифференциальное уравнение I порядка.
Если
),(xzy
=
′
то
)(xzy
′
=
′
′
, тогда уравнение примет вид:
.0) ; ;(
=
′
zzxF
Решим
это уравнение относительно
), ;()(
1
Cxxz
ϕ
=
и найдем у из уравнения
1
;( Cxy
ϕ
=
′
:
),
1
;( Cx
dx
dy
ϕ
=
,
.
3) Уравнение вида
0) ; ;(
=
′
′
′
yyyF
не содержит переменную х . Введем новую
функцию
)(yz
такую, что
.yz
′
=
.
)(
z
dy
dz
dx
dy
dy
dz
dx
dy
dy
yd
dx
yd
y ⋅=⋅=⋅
′
=
′
=
′′
Уравнение примет вид
.0) ; ;( =
′
y
zzyF
Решив это уравнение, найдем
). ;() ;(
11
CyyCyz
ϕ
ϕ
=
′
⇒
=
∫
+=⇒=
=
2
11
1
) ;() ;(
,) ;(
Cx
Cy
dy
dx
Cy
dy
dxCydy
ϕϕ
ϕ
- общее решение уравнения.
Пример 6. найти общее решение дифференциального уравнения:
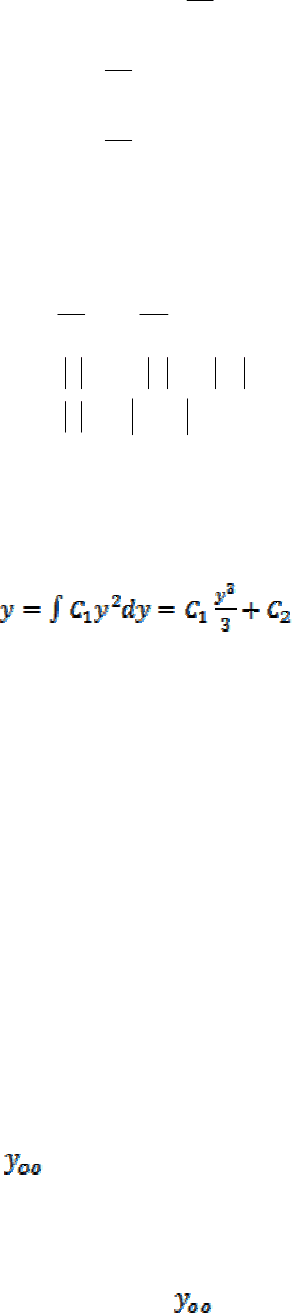
168
,2
,2
,02
, ,
,0)(2
2
2
2
2
dyzdzzy
z
dy
dz
zy
z
dy
dz
zy
z
dy
dz
yzy
yyy
=⋅⋅
=⋅⋅
=−⋅⋅
⋅=
′′
=
′
=
′
−
′′
⋅
Разделяя переменные и интегрируя, получим
.
,
,lnln
,lnln2ln
,2
2
1
2
1
2
1
1
yCy
yCz
yCz
Cyz
y
dy
z
dz
=
′
=
=
+=
=
∫ ∫
Интегрируя последнее равенство, найдем общее решения уравнения у.
.
Линейные дифференциальные уравнения II порядка с постоянными коэффи-
циентами. Линейным дифференциальным уравнением II порядка с постоян-
ными коэффициентами называется уравнение вида:
)(xrqyypy
=
+
′
+
′
′
,
Если
,0)(
=
xr
то уравнение
0
=
+
′
+
′
′
qyypy
называется линейным однород-
ным дифференциальным уравнением II порядка с постоянными коэффициен-
тами.
Общее решение линейного однородного дифференциального уравнения II
порядка с постоянными коэффициентами ищется с помощью характеристи-
ческого уравнения
0
2
=++ qpkk
. Характеристическое уравнение получается
из уравнения
0
=
+
′
+
′
′
qyypy
заменой
. , ,
02
kykyky →→
′
→
′′
Т. к. характери-
стическое уравнение квадратное, то оно имеет не более двух корней.
Справедливо утверждение:
1) если корни характеристического уравнения действительны и различны,
,
21
kk
≠
то общее решение однородного уравнения
0
=
+
′
+
′
′
qyypy
имеет
вид:
xkxk
oo
eCeCy
21
21
+=
2) если корни характеристического уравнения действительны и равные,
,
21
kkk
=
=
то общее решение уравнения имеет вид:
kxkx
oo
xeCeCy
21
+=
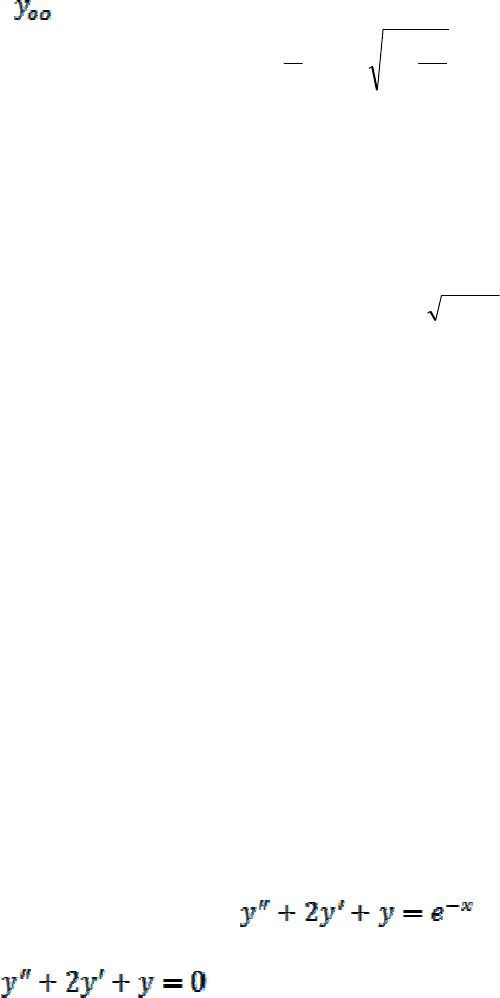
169
3) если характеристическое уравнение не имеет действительных корней, то
общее решение уравнения
имеет вид:
),sincos(
21
xCxCey
x
oo
ββ
α
+=
где
4
,
2
2
p
q
p
−=−=
βα
.
Пример 7. Найти общее решение следующих уравнений:
а)
02
=
−
′
+
′
′
yyy
б)
02
=
+
′
−
′
′
yyy
в)
0134
=
+
′
−
′
′
yyy
)3sin3cos(
3413 ,2 1 1 ,2
036134)4( 0)1( 981
0134 012 02
21
2
212
2
1
2121
22
222
xCxCeyxeCeCyeCeCy
kkkk
DkD
kkkkkk
x
oo
xx
oo
xx
oo
+=+=+=
=−=====−=
<−=⋅−−==−=+=
=+−=+−=−+
−
βα
Решение неоднородных уравнений II порядка с постоянными коэффициента-
ми
)(xrqyypy
=
+
′
+
′
′
.
а) Метод вариации произвольной постоянной.
Находим общее решение соответствующе
го однородного уравнения в виде
2211
yCyCy
+
=
,
где
1
y и
2
y − функции, зависящие от
x
.
Предполагаем, что
1
C и
2
C − функции от переменной
,
x
т. е.
2211
)()( yxCyxCy
+
=
Функции
)(
1
xC и )(
2
xC , находятся из системы дифференциальных уравнений
=
′′
+
′′
=
′′
+
′′
).(
,0
2211
2211
xryCyC
yCyC
Решив эту систему, в которой
1
C и
2
C неизвестные, а
1
y и
2
y ;
1
y
′
и
2
y
′
− ко-
эффициенты найдем
1
C и
2
C , а следовательно и общее решение данного
уравнения.
Пример 8. Найти общее решение уравнения
.
Рассмотрим линейное однородное дифференциальное уравнение
,
составим соответствующее характеристическое уравнение и найдем его об-
щее решение.
xx
oo
xeCeCy
kk
kk
−−
+=
−==
=++
21
21
2
1
012
Будем искать общее решение данного уравнения в виде:
xx
xexCexCy
−−
+= )()(
21
.
Запишем систему дифференциальных уравнений и решим ее.
=−
′
+
′
=
′
+
′
−−−−
−−
.)(
,0
21
21
xxxx
xx
exeeCeC
xeCeC
=−
′
+
′
−
=
′
+
′
.1)1(
,0
21
21
xCC
xCC
Получим
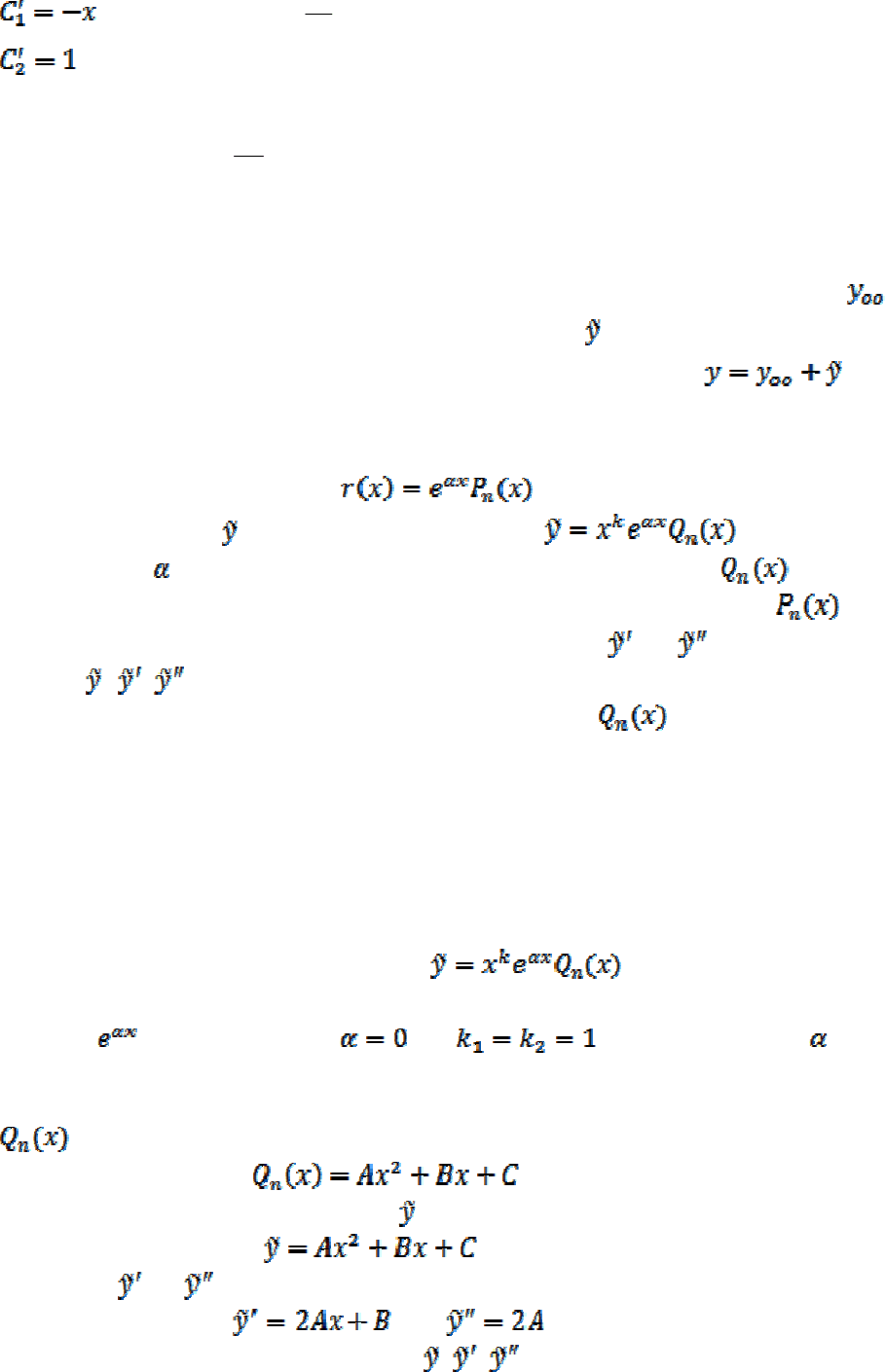
170
, откуда
1
2
1
2
D
x
C +−=
.
, откуда
22
DxC
+
=
.
Таким образом, общее решение исходного уравнения имеет вид:
x
xeDx
x
eD
x
y
−
++
−
+−=
)
2
(
1
2
2
.
б) Метод неопределенных коэффициентов.
Общее решение линейного неоднородного уравнения находится так:
1. Найти общее решение соответствующего однородного уравнения
.
2. Найти одно какое-нибудь частное решение
.
3. Общее решение найти как сумму этих двух решений:
.
Рассмотрим случай, когда правая часть уравнения
)(xrqyypy
=
+
′
+
′
′
имеет специальный вид
.
Частное решение
будем искать в виде г где k число
совпадений
с корнями характеристического уравнения; - много-
член с неопределенными коэффициентами той же степени, что и
.
Способ решения заключается в следующем: найти
и , подставить зна-
чения
, , в данное уравнение, и методом неопределенных коэффици-
ентов найти значения коэффициентов многочлена
.
Пример 9. Найти общее решение уравнения
.2
2
xyyy =+
′
−
′′
1) ищем общее решение соответствующего однородного уравнения:
1
012
0
2
21
2
==
=+−
=
+
′
−
′
′
kk
kk
y
y
y
.
21
xx
oo
xeCeCy +=
2) частное решение ищем в виде
.
Так как правая часть исходного уравнения
2
2 xyyy =+
′
−
′′
не содержит мно-
житель
, следовательно, , и , т.е. совпадений с
корнями характеристического уравнения нет, то получим k = 0.
В правой части исходного уравнения стоит многочлен второй степени, значит
запишется в виде
.
Таким образом, частное решение
запишется как
.
Находим
и :
, .
Подставляем в уравнение значения , , , получим
