Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

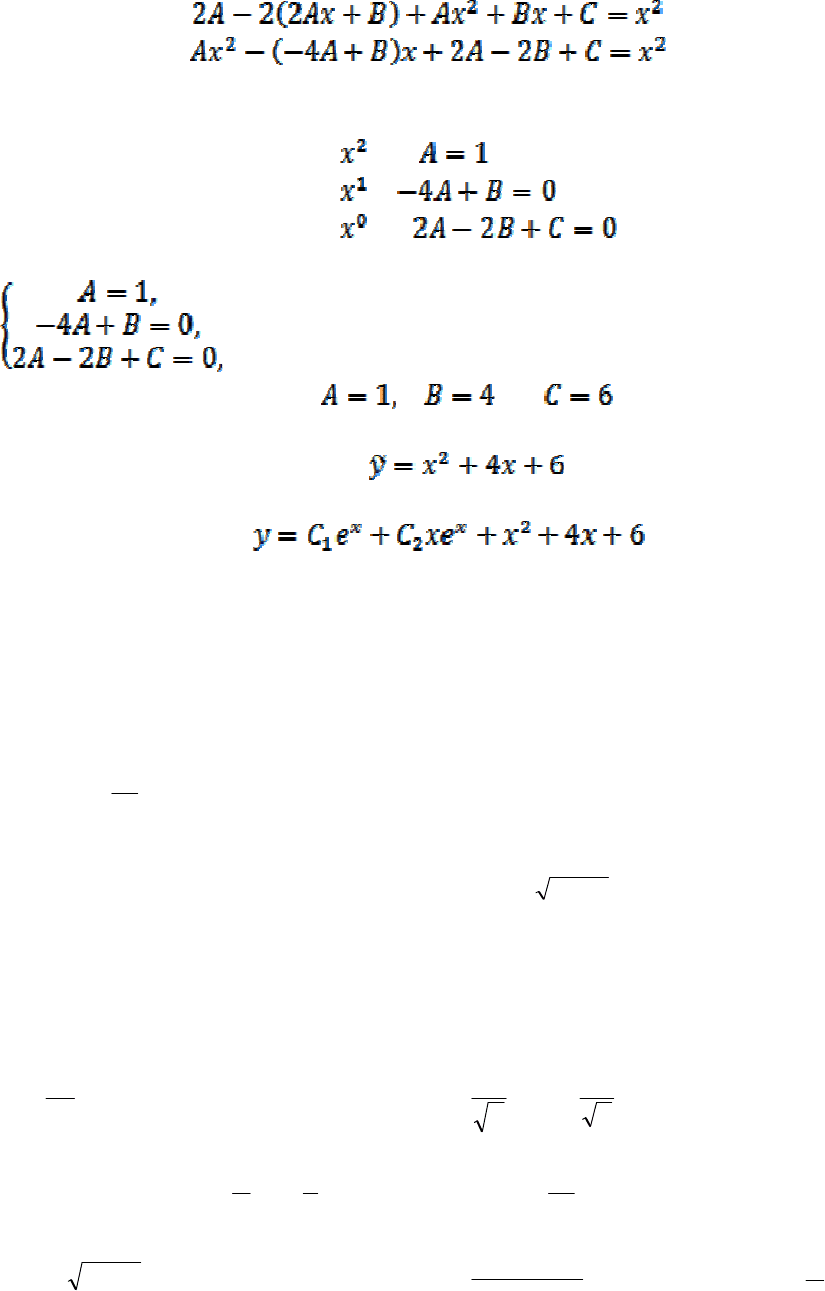
171
,
,
Приравниваем коэффициенты при неизвестных при одинаковых степенях х
в левой и правой частях равенства:
: ,
: ,
: .
Получили систему трех уравнений с тремя неизвестными:
решая которую находим
, .
Таким образом
.
Общее решение уравнения запишется так:
.
Задачи для самостоятельного решения.
Уравнения с разделяющимися переменными.
Найти общие решения дифференциальных уравнений:
1.
( )xy x
dx
dy
+ = 1
.
2.
( ) ( )xy x dx x y y dy
2 2
0+ + − =
.
3.
( ) ( )y x y dy x xy dx− + + =
2 2
0
.
4.
( ) ( )1 0
2
+ − + =x dy xy x dx
.
5.
x y xy y
2
2 3
′
− =
.
6.
(sin ) lnx y y y
′
=
.
7.
e x dy x e dx
y y
( ) ( )1 2 1 0
2
+ − + =
.
8.
cos sin ( )x ydy x e dx
y
− + =2 1 0
.
9.
1 0
2
−
′
+ =x y xy
.
10.
′
=y x e
x2
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
данным начальным условиям:
11.
dy
y
dx
2
0− =
;
y
(
)
0
3
=
. 12.
dy
y
dx
dx
x
+ =
;
y
(
)
0
1
=
.
13.
tgx y y
⋅
′
=
+
1
;
y( )
π
6
1
2
= −
. 14.
( )1 0
2
− + =x
dy
dx
xy
;
y
(
)
0
4
=
.
15.
′
− =y x xy1
2
;
y
(
)
1
0
=
. 16.
dx
x y
ctgx ydy
cos cos
sin
2
0+ =
;
y( )
π
π
3
=
.
Уравнения с разделяющимися переменными.
17. ( ) ( )1 2 3 0
2
+ − + =x dy x y dx
;
y
(
)
0
1
=
−
.
18.
x y dx y x dy( ) ( )
6 2 4
1 1 0+ + + =
;
y
(
)
0
1
=
.
172
19.
1 2
1
0
+
+
+
′
=
cos
sin
x
y
y
;
y( )
π
4
0=
.
20.
′
+
−
=
+
y x y x ysin( ) sin( )
;
y( )
π
π
=
2
.
Однородные уравнения.
Найти общие решения дифференциальных уравнений:
21.
( )x y dx xdy
+
+
=
0
.
22.
′
=
+
y
x y
xy
2 2
.
23.
x y y xy x
2 2 2
′
= − +
.
24. ( )x y ydx x dy− =
2
.
25.
xy y x y
′
− = +
2 2
.
26.
xy dy x y dx
2 3 3
= +( )
.
27.
dy
dx
y
x
y
x
= − +
2
2
1
.
28.
′
=
−
−
y
xy y
x xy
2
2
2
.
29.
xy y y x
′
=
−
(ln ln )
.
30.
xy y x
y
x
′
= + cos
2
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
начальным условиям:
31.
′
=
+
y
x y
x
2
2
;
y
(
)
1
0
=
.
32.
′
=
+
y
xy y
x
2
2
;
y
(
)
1
1
=
.
33.
( )
x y dx xdy
−
+
=
0
;
y
(
)
1
0
=
.
34.
y dx x xy dy
2 2
0+ − =( )
;
y
(
)
1
1
=
.
35.
′
+ =y x xy y( )
2 2
;
y
(
)
2
2
=
.
36.
xy y xtg
y
x
′
− =
;
y( )1
2
=
π
.
37.
xy xe y
y
x
′
= +
;
y
(
)
1
0
=
.
38.
( )xy y arctg
y
x
x
′
− =
;
y
(
)
1
0
=
.
39.
′
= +y
y
x
y
x
sin
;
y( )1
2
=
π
.
40.
′
=
− −
+ −
y
y xy x
y xy x
2 2
2 2
2
2
;
y
(
)
1
1
=
−
.
Линейные дифференциальные уравнения первого порядка. Уравнения Бернул-
ли.
Найти общие решения дифференциальных уравнений:
41.
′
+
=
y xy x
4
.
42.
′
= −y
y
x
1
.
43.
dy
dx
y e
x
+ =
−
.
44.
′
− = −y xy x x e
x
2
3
2
( )
.
45.
x y xy
2
2 3
′
= −
.
46.
( ) ( )1 2 1
2 2 2
+
′
− = +x y xy x
.
47.
x y y x e
x
( ) ( )
′
− = +1
2
.
48.
′
−
+
= +y
y
x
x
2
1
1
3
( )
.
49.
′
+ =y xy x2 2
3
.
50.
′
−
=
y y x x x
sin sin cos
.
51.
( )1
2
+
′
+ =x y y arctgx
.
52.
′
− =y x x y x xln ln3
3 2
.
53.
′
+ =
−
y xe y e
x x e
x
( )1
.
54.
y xy y y
=
′
+
′
ln
.
55.
′
=
+ −
y
y
y y y x2 ln
.
56.
′
+ =y xy xy2 2
2
.
57.
3 2
2 3 3
xy y y x
′
− =
.
58.
2
1
′
+ =
−
y x
y
x
y xln cos
.
59.
′
− =y y x y xcos cos
2
.
60.
( ln )x y x y y
2
−
′
=
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
указанным начальным условиям.
173
61.
xy y
′
+
=
3
;
y
(
)
1
0
=
.
62.
′
−
+
=
y y
2 3 0
;
y
(
)
0
1
=
.
63.
xy y x e
x
′
− =2
3
;
y
(
)
1
0
=
.
64.
′
− =y ytgx
x
1
cos
;
y
(
)
0
0
=
.
65.
xy y x
′
+
=
+
1
;
y
(
)
2
3
=
.
66.
′
− + =y x y x1
2
arcsin
;
y
(
)
0
0
=
.
67.
′
− =y
y
x
x
x x
ln
ln
;
y e
e
( ) =
2
2
.
68.
′
+ =y y e y
x
2
;
y( )0
9
4
=
.
69.
′
+
+
= +y
x y
x
y x x
3
1
1
2
3
2 3
( ) sin
;
y
(
)
0
1
=
.
70.
( )y y x y x
2 2
2 2 0+ +
′
+ =
;
y
(
)
1
0
=
.
Дифференциальные уравнения, допускающие понижение порядка.
Найти общие решения дифференциальных уравнений:
71. y x
IV
=
.
72.
′
′
′
=
+
y x x
cos
.
73.
′′′
=y x xsin sin
4
2
.
74.
′
′
=
y x x
2 ln
.
75.
y e
n ax
( )
=
.
76.
xy y
′
′
+
′
=
0
.
77.
x x y y
ln
⋅
′
′
=
′
.
78.
xy y y x
′
′
=
′
′
−
(ln ln )
.
79.
2
2 2
xy y y a
′′′
⋅
′′
=
′′
−( )
.
80.
′′
− ⋅
′
=y ctgx y x2
3
sin
.
81.
′′
= +
′
y y
1
2
( )
.
82.
2 3 4
2 2
yy y y
′′
−
′
=( )
.
83.
y y y y y( ln ) ( ln )( )1 1 0
2
−
′′
+ +
′
=
.
84.
′′
=
′
y
y
y
.
85.
yy y y y
′′
−
′
=
′
( )
2 2
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
указанным начальным условиям:
86.
′′
+ =y x( )2 1
5
;
y y( ) , ( )− =
′
− = −1
1
12
1
1
4
.
87.
′′
=y xe
x
;
y y
( ) ( )0 0 0
=
′
=
.
88.
′
′
′
=
y x x
sin
;
y y y
( ) , ( ) , ( )0 0 0 0 0 2
=
′
=
′
′
=
.
89.
′′
=y
x
1
2
cos
;
y y( ) , ( )0 1 0
3
5
=
′
=
.
90.
′′
+ =
′
y x xy( )
2
1 2
;
y y
( ) , ( )0 1 0 3
=
′
=
.
91.
2
2
′′
=
′
+
′
y
y
x
x
y
;
y y( ) , ( )1
2
5
1
2
2
=
′
=
.
92.
′
′
′
−
−
′
′
=
y x y
( )1 0
;
y y y
( ) , ( ) , ( )2 2 2 1 2 1
=
′
=
′
′
=
.
93.
′
′
=
′
y yy
2
;
y y
( ) ( )0 0 1
=
′
=
.
94.
′′
−
′
−
= −y
y
x
x x
1
1( )
;
y y
( ) , ( )2 1 2 1
=
′
=
−
.
95.
yy y y y
′′
−
′
=( ) ln
2 2
;
y y
( ) , ( )0 1 0 1
=
′
=
.
Линейные дифференциальные уравнения второго порядка с постоянными ко-
эффициентами.
Найти общие решения дифференциальных уравнений:
96.
′
′
−
=
y y
0
.
97.
′
′
−
′
+
=
y y y
4 3 0
.
98.
′
′
+
′
−
=
y y y
2 0
.
99.
′
′
−
′
+
=
y y y
5 4 0
.
100.
′
′
−
′
+
=
y y y
2 0
.
101.
′′
−
′
+ =y y y
1
4
0
.
102.
′
′
−
′
+
=
y y y
6 9 0
.
103.
′
′
+
=
y y
0
.
104.
′
′
−
′
+
=
y y y
2 2 0
.

174
105.
′
′
+
′
+
=
y y y
6 13 0
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
указанным начальным условиям:
106.
′
′
−
=
y y
9 0
;
y y
( ) , ( )0 2 0 6
=
′
=
.
107. 107.
′
′
+
′
+
=
y y y
3 2 0
;
y y
( ) , ( )0 1 0 3
=
−
′
=
.
108.
′
′
−
′
+
=
y y y
4 3 0
;
y y
( ) , ( )0 6 0 10
=
′
=
.
109.
′
′
+
′
+
=
y y y
6 9 0
;
y y
( ) , ( )0 2 0 3
=
′
=
.
110.
′
′
−
′
+
=
y y y
2 2 0
;
y y
( ) , ( )0 1 0 3
=
′
=
.
Найти общие решения дифференциальных уравнений:
111.
′
′
+
′
−
=
y y y
2 3 1
.
112.
′
′
+
′
=
y y
3 3
.
113.
′
′
+
′
−
=
y y y
4 5 2
.
114.
2 2
′′
+
′
− =y y y e
x
.
115.
′′
+
′
=y y e
x
3
.
116.
′′
+
′
+ =
−
y y y e
x
2 6
.
117.
′′
−
′
+ =y y y e
x
8 17 10
2
.
118.
′
′
+
′
−
=
y y y x
2 3
.
119.
′′
−
′
+ = − +y y y x x6 9 2 3
2
.
120.
′
′
+
′
=
−
y y x
2 1
.
121.
′′
−
′
= −y y x7 1
2
( )
.
122.
′′
+
′
− = +y y y x e
x
6 6 1
3
( )
.
123.
′′
−
′
= +y y x e
x
2 4 4
2
( )
.
124.
′′
−
′
=y y xe
x
4
4
.
125.
4 3
3
4
′′
−
′
=y y xe
x
.
126.
′
′
+
=
y y x
4 sin
.
127.
′
′
+
=
y y x
25 5cos
.
128.
′
′
+
=
y y x
16 8 4cos
.
129.
′
′
+
′
+
=
−
y y y x
6 13 75 2sin
.
130.
′
′
−
′
+
=
+
y y y x x
3 2 3 19cos sin
.
131.
′
′
−
′
−
=
−
y y y x x
2 8 12 2 36 2sin cos
.
132.
′′
+
′
+ =
−
y y y e x
x
6 13 2
3
cos
.
133.
′′
−
′
+ = −y y y e x x
x
4 8 2 2
2
(sin cos )
.
134.
′
′
+
=
y y x x
4 cos
.
135.
′′
+ =y y x x
2
sin
.
136.
′
′
−
′
+
=
+
y y y x x
3 2 3 5 2sin
.
137.
′
′
−
′
+
=
+
y y y x x
4 4 2 2 2sin
.
138.
′′
−
′
+ = +
−
y y y e
x
3 2 1
2
.
139.
′′
−
′
− = +
−
y y y e e
x x
2
2
.
140.
′′
+
′
= −
−
y y x e
x
2
.
141.
′′
−
′
= + + +y y e x x
x
3 1 cos sin
.
142.
′′
+ =y y
x
1
sin
.
143.
′′
+
′
+ =
+
y y y
e
x
5 6
1
1
2
.
144.
′′
+ =y y
x
1
3
cos
.
145.
′′
−
′
+ =
+
y y y
e
x
x
2
1
2
.
Найти частные решения дифференциальных уравнений, удовлетворяющие
указанным начальным условиям:
146.
′
′
−
′
−
=
y y y
6 2
;
y y
( ) , ( )0 1 0 0
=
′
=
.
147.
′
′
−
=
−
y y x
9 2
;
y y
( ) , ( )0 0 0 1
=
′
=
.
148.
′′
+
′
+ = + +y y y x x2 2 2 8 6
2
;
y y
( ) , ( )0 1 0 4
=
′
=
.
149.
′′
+
′
= + +y y x x2 6 2 1
2
;
y y
( ) , ( )0 2 0 2
=
′
=
.
150.
′
′
−
′
=
−
y y x
2 2
;
y y
( ) , ( )0 1 0 1
=
′
=
.
151.
′′
−
′
+ =y y y e
x
4 3
5
;
y y
( ) , ( )0 3 0 9
=
′
=
.
152.
′′
+
′
+ = +
−
y y y x e
x
2 18 8( )
;
y y
( ) , ( )0 2 0 0
=
′
=
.
153.
′′
−
′
+ =y y y xe
x
4 20 16
2
;
y y
( ) , ( )0 1 0 2
=
′
=
.
154.
′
′
+
=
y y t
4 2 2cos
;
y y
( ) , ( )0 0 0 4
=
′
=
.
155.
′
′
−
′
+
=
−
−
y y y x x
3 2 7sin cos
;
y y
( ) , ( )0 2 0 7
=
′
=
.

175
8. РЯДЫ
Числовым рядом называется выражение
∑
∞
=
+++++=
1
321
n
nn
uuuuu KK
,
а числа
KK
n
uuuu
321
,,
членами ряда
. Эти числа образуют бесконечную чи-
словую последовательность. Чтобы задать ряд, надо задать формулу
n
-го
(общего) члена ряда u
n
=f(n).
Сумма
n
первых членов ряда называется
n-ой
частичной суммой
ряда и обозначается
n
n
nn
uuuuuS ++++==
∑
∞
=
K
321
1
.
Если существует предел
S
бесконечной последовательности
}{
n
S
час-
тичных сумм, то есть
SS
n
n
=
∞→
lim
, то этот предел называется
суммой ряда
, а
сам ряд в этом случае называют
сходящимся
. Если же предел
n
n
S
∞→
lim
не су-
ществует, то ряд называют
расходящимся
. Расходящийся ряд суммы не име-
ет.
Необходимый признак сходимости.
Если ряд
∑
∞
=
1
n
n
u
сходится, то его общий член стремится к нулю при
∞
→
n
,
т.е.
0lim =
∞→
n
n
u
.
Из необходимого признака следует , что если
0lim ≠
∞→
n
n
u
, то ряд расходится.
Пример 1.
Исследовать сходимость ряда
0,
12
0
≠+++++=
−
∞
=
∑
aaqaqaqaaq
n
n
n
KK
.
Данный ряд является бесконечной геометрической прогрессией и его n-
ая частичная сумма
n
S
совпадает с суммой n первых членов геометрической
прогрессии, поэтому
q
qa
aqaqaqaS
n
n
n
−
−
=++++=
−
1
)1(
12
K
.

176
Найдем предел этой суммы
q
q
a
q
a
q
qa
S
n
n
n
n
n
n
−
−
−
=
−
−
=
∞→∞→∞→
1
lim
11
)1(
limlim
. В зависимо-
сти от величины q возможны случаи:
1. Если
1<q
, то
0
→
n
q
при
∞
→
n
. Поэтому
q
a
S
n
n
−
=
∞→
1
lim
, исходный ряд схо-
дится и его сумма равна
q
a
−
1
.
2. . Если
1>q
, то
∞→
n
q
при
∞
→
n
. Поэтому
∞=
∞→
n
n
S
lim
, исходный ряд рас-
ходится.
3. . Если
1=q
, то при
1
=
q
ряд приобретает вид a+a+a+…+a+…, для него
naS
n
=
и
∞=
∞→
n
n
S
lim
, т.е. ряд расходится. При
1
−
=
q
ряд приобретает вид a-
a+a-a+…, для него
0
=
n
S
при четном n и
aS
n
=
при нечетном n. Следователь-
но
n
n
S
∞→
lim
не существует и исходный ряд расходится.
Таким образом, ряд геометрической прогрессии сходится при
1<q
и рас-
ходится при
1≥q
.
Пример 2. Выяснить, сходится ряд или расходится
.
1
0
2
2
∑
∞
=
+
n
n
n
Общий член этого ряда
2
2
1
n
n
u
n
+
=
и
1
1
1
1
lim
1
limlim
2
2
2
=
+
=
+
=
∞→∞→∞→
n
n
n
u
nn
n
n
. Так как
0lim
≠
∞→
n
n
u
, то на основании необхо-
димого признака ряд расходится.
Достаточные признаки сходимости рядов с положительными членами.
Рассмотрим числовые ряды с положительными членами
177
∑
∞
=
1
n
n
u
(1) и
∑
∞
=
1
n
n
v
(2).
Первый признак сравнения.
Если, начиная с некоторого
N
для всех членов рядов (1), (2) при
n
>
N
выполняется неравенство u
n
< v
n
,
то
1) ряд (1) сходится, если сходится ряд (2);
2) ряд (2) расходится, если расходится ряд (1).
Второй признак сравнения.
Если существует конечный и отличный от нуля предел
0lim
≠=
∞→
A
v
u
n
n
n
,
то ряды (1) и (2) или оба сходятся или оба расходятся.
При использовании признаков сравнения исследуемый ряд часто срав-
нивают или с бесконечной геометрической прогрессией или с расходящимся
гармоническим рядом
∑
∞
=
1
1
n
n
. Можно сравнивать и с другими известными ря-
дами.
Признак Даламбера.
Пусть для ряда (1) с положительными членами
существует конечный предел
q
u
u
n
n
n
=
+
∞→
1
lim
. Тогда:
1) ряд (1) сходится, если q<1;
2)
ряд (1) расходится, если q>1;
3)
в случае q=1 ряд (1) может оказаться как сходящимся, так и расхо-
дящимся, вопрос о сходимости ряда остаётся открытым.
Радикальный признак Коши.
Пусть для ряда (1) с положительными членами существует конечный пре-
дел
qu
n
n
n
=
∞→
lim
.
Тогда: 1) ряд (1) сходится, если q<1;
178
2)
ряд (1) расходится, если q>1;
3)
в случае q=1 ряд (1) может оказаться как сходящимся, так и расхо-
дящимся, вопрос о сходимости ряда остаётся открытым.
Интегральный признак Коши.
Если f(x) неотрицательная невозрастающая функция при x>0, причём f(n) =
u
n
, то ряд (1) сходится или расходится одновременно с интегралом
∫
∞
1
)( dxxf
.
Пример 3.
Используя признак сравнения, исследовать сходимость ряда
∑
∞
=
+
1
31
1
n
n
.
Сравним данный ряд с рядом бесконечной геометрической прогрессии
∑
∞
=1
3
1
n
n
, который сходится так как
1
3
1
<=
q
. Имеем
nn
3
1
3
1
1
<
+
. Следовательно,
по первому признаку сравнения ряд сходится.
Пример 4.
Используя признак сравнения, исследовать сходимость ряда
∑
∞
=1
1
sin
n
n
.
Сравним данный ряд с гармоническим рядом
∑
∞
=1
1
n
n
, который является
расходящимся. Имеем
1
sin
lim
0
1
1
1
sin
limlim
0
==
→
=
==
→∞→∞→
t
t
t
t
n
n
n
v
u
tn
n
n
n
. По второму при-
знаку сравнения гармонический ряд и данный ряд ведут себя одинаково, по-
этому из расходимости гармонического ряда следует расходимость данного
ряда.
Пример 5.
Исследовать сходимость ряда с помощью признака Даламбера
∑
∞
=
+
1
!2
1
n
n
n
n
.

179
Имеем
!
2
1
n
n
u
n
n
+
=
,
)!1(2
2
)!1(2
1)1(
11
1
+
+
=
+
+
+
=
++
+
n
n
n
n
u
nn
n
, тогда
0
)
1
1(
21
lim
2
1
)1(
2
lim
2
1
)!1(2)1(
!2)2(
limlim
2
2
2
21
1
=
+
+
=
+
+
=
++
+
==
∞→∞→
+
∞→
+
∞→
n
nn
n
n
nn
nn
u
u
q
nn
n
n
n
n
n
n
. Так как q<1, то
согласно признаку Даламбера ряд сходится.
Пример 6.
Исследовать сходимость ряда с помощью радикального признака
Коши
∑
∞
=
−
+
1
32
13
n
n
n
n
.
Имеем
n
n
n
n
u
−
+
=
32
13
, тогда
2
3
32
13
lim
32
13
limlim =
−
+
=
−
+
==
∞→∞→∞→
n
n
n
n
uq
n
n
n
n
n
n
n
.
Так как q>1, то согласно признаку Коши ряд расходится.
Пример 7.
Исследовать сходимость ряда с помощью интегрального призна-
ка Коши
∑
∞
=1
2
ln
n
n
n
.
Используя общий член ряда
n
n
u
n
2
ln
=
, составим функцию
x
x
xf
2
ln
)( =
.
Вычислим интеграл
∞=−===
∞→∞→
∞
∞∞
∫∫
3
1ln
lim
3
ln
lim
3
ln
)(lnln
ln
33
1
3
1
2
1
2
xx
xx
xxdldx
x
x
. Интеграл расходится,
следовательно данный ряд расходится.
Знакопеременные ряды.
Числовой ряд
∑
∞
=1n
n
u (3), содержащий как положительные так и отрицатель-
ные члены, называется знакопеременны.
Достаточный признак сходимости знакопеременного ряда
180
Пусть ряд (3)является знакопеременным. Рассмотрим ряд, составленный
из абсолютных величин членов данного ряда:
∑
∞
=1n
n
u (4).
Если ряд (4) сходится, то и ряд (3) тоже сходится. Ряд (3) при этом на-
зывается абсолютно сходящимся. Если ряд (3) сходится, а (4) расходится, то
ряд (3) называется условно (не абсолютно) сходящимся.
Знакочередующиеся ряды.
Знакопеременный ряд вида
∑
∞
=
−
1
)1(
n
n
n
u , (u
n
>0) называется знакочередующим-
ся.
Признак Лейбница.
Если члены знакочередующегося ряда, начиная с некоторого номера N,
1) монотонно убывают по абсолютной величине
...
21.
>>>
++ NNN
uuu
и
2) стремятся к нулю
0lim =
∞→
n
n
u
,
то ряд сходится и его сумма не превышает первого члена ряда.
Пример 8.
Исследовать сходимость ряда Лейбница
n
n
n
1
)1(
1
1
∑
∞
=
+
− .
Данный ряд сходится по признаку Лейбница так как
...
1
...
3
1
2
1
1 >>>>>
n
. и
0
1
lim =
∞→
n
n
. В то же время, ряд, составленный из абсолютных величин его чле-
нов,
n
n
1
1
∑
∞
=
расходится (гармонический ряд). Таким образом, ряд Лейбница -
условно (не абсолютно) сходящийся ряд.
ФУНКЦИОНАЛЬНЫЕ РЯДЫ.
