Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

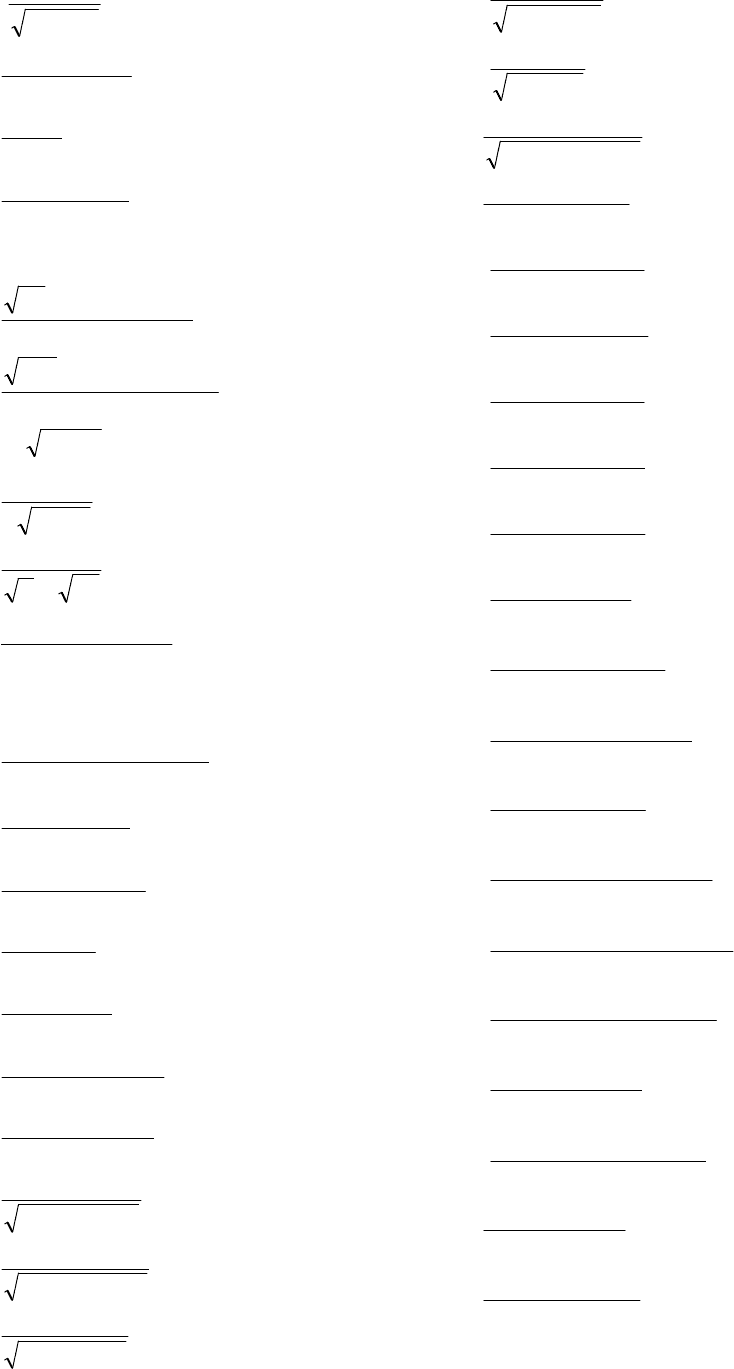
121
38.
e dx
e
x
x
2 4−
∫
;
39.
( )
cos
5 3
7
2
tgx dx
x
−
∫
;
40.
ln xdx
x
∫
;
41.
dx
x x( ln )2 5
3
−
∫
;
42.
sin ( cos )x x dx4 5
8
−
∫
;
43.
x x x dx
x
3 5
6
4 9
9
+
∫
ln( )
;
44.
8 2 6
3
73
9
2
x x x dx
x
+
∫
log ( )
;
45.
x x dx
3 2
3−
∫
;
46.
dx
x x
2
1−
∫
;
47.
dx
x x+
∫
3
;
48.
∫
⋅ )3ln(2sin tgxx
dx
;
49.
tgx x dx⋅ ⋅
∫
ln(cos )
;
50.
dx
x x xcos ( sin cos )2 5−
∫
51.
−
+
− + −
∫
2 7
4
8
2
x
x
x
dx
.
52.
x
x
x
dx
−
+ +
∫
5
2
12
10
2
.
53.
−
−
− −
∫
6 4
6
2
x
x
x
dx
.
54.
7 5
4
8
2
x
x
x
dx
+
+ +
∫
.
55.
5 5
3
18
39
2
x
x
x
dx
+
− + −
∫
.
56.
−
+
− − +
∫
4 5
2
4
16
2
x
x
x
dx
.
57.
−
+
− +
∫
2 2
6 58
2
x
x x
dx
.
58.
−
−
− − +
∫
6 11
6 7
2
x
x x
dx
.
59.
x
x x
dx
−
− −
∫
4
6 5
2
.
60.
−
+
− +
∫
4 6
6
2
x
x x
dx
.
61.
−
+
−
∫
7 14
2
2
x
x x
dx
.
62.
−
+
− + +
∫
3 13
4 12
2
x
x x
dx
.
63.
2 20
2 4 4
x
x x
dx
−
+ −
∫
( )( )
;
64.
6 2
4 3 2 5
x
x x
dx
+
− +
∫
( )( )
;
65.
−
+
− −
∫
8 22
2 7 2 4
x
x x
dx
( )( )
;
66.
−
−
+ −
∫
14 2
3 6 4 5
x
x x
dx
( )( )
;
67.
4 18
3 6 4 3
x
x x
dx
−
− −
∫
( )( )
;
68.
−
−
+ +
∫
22 19
4 4 2 1
x
x x
dx
( )( )
;
69.
−
+
− −
∫
8 20
1 3 7
x
x x
dx
( )( )
;
70.
− − +
− +
∫
27 63 18
3 2 3 7
2
x x
x x
dx
( )( )
;
71.
6 31 68 5
7 2 3
3 2
x x x
x x
dx
+ − −
+ −
∫
( )( )
;
72.
8 26 12
4 1 2 4
3 2
x x
x x
dx
+ −
+ +
∫
( )( )
;
73.
− − − +
+ −
∫
16 32 8 2
2 4 1
3 2
x x x
x x
dx
( )( )
;
74.
− − + +
− +
∫
16 16 36 16
2 2 4 6
3 2
x x x
x x
dx
( )( )
;
75.
18 42 14 56
3 5 2 4
3 2
x x x
x x
dx
− − +
− −
∫
( )( )
;
76.
− + +
− +
∫
2 7 21
2 6 1
3
x x
x x
dx
( )( )
;
77.
12 18 42 4
4 6 2
3 2
x x x
x x
dx
+ − −
− +
∫
( )( )
.
78.
− − −
+ −
∫
7 3 5
2 1
2
2
x x
x x
dx
( )( )
;
79.
14 52 46
1 3
2
2
x x
x x
dx
+ +
− +
∫
( )( )
;
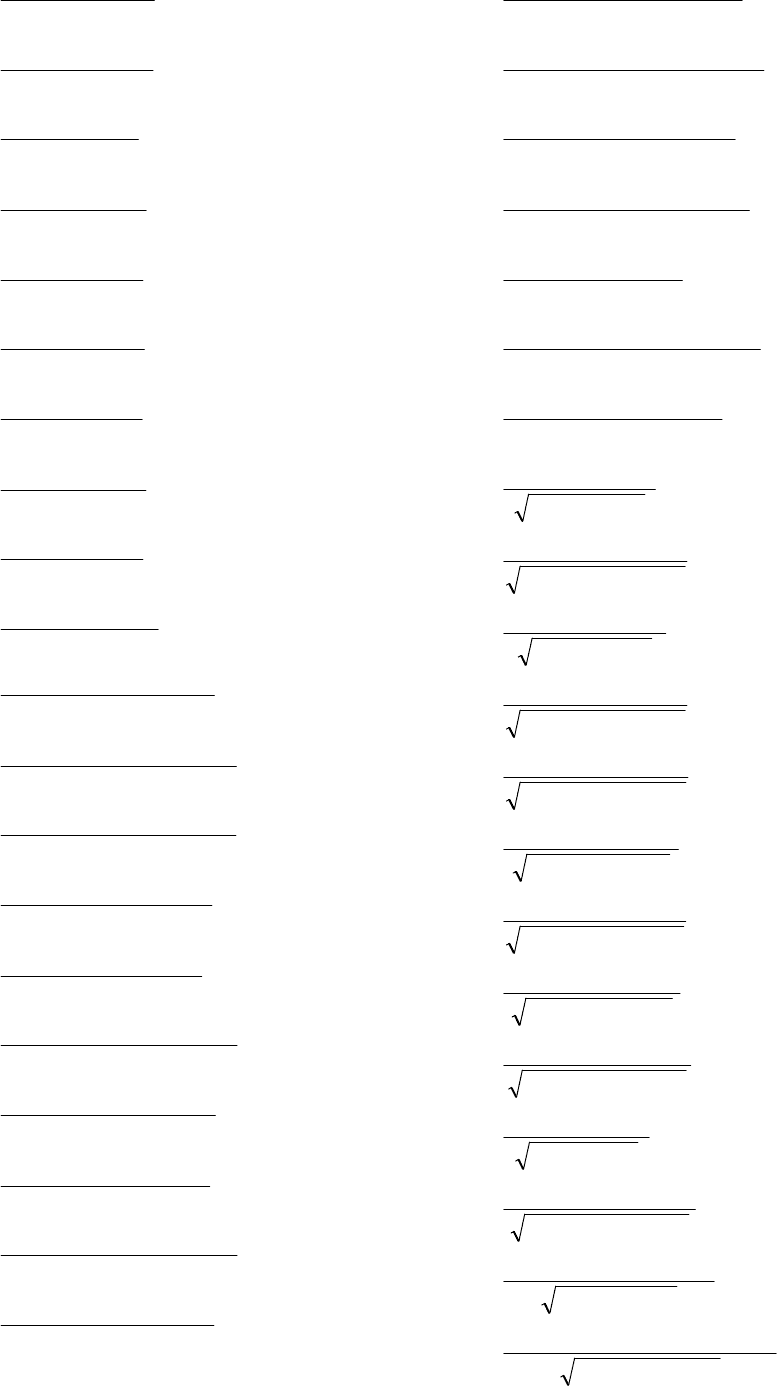
122
80.
− − +
− −
∫
2 4 24
4 2
2
2
x x
x x
dx
( )( )
;
81.
− − +
+ −
∫
x x
x x
dx
2
2
30 40
2 2( )( )
;
82.
4 20 4
1 1
2
2
x x
x x
dx
− +
+ −
∫
( )( )
;
83.
8 47 54
2 4
2
2
x x
x x
dx
− +
+ −
∫
( )( )
;
84.
3 16 17
2 1
2
2
x x
x x
dx
− +
− −
∫
( )( )
;
85.
x x
x x
dx
2
2
6 58
4 3
+ +
− +
∫
( )( )
;
86.
x x
x x
dx
2
2
16 21
1 2
− +
− −
∫
( )( )
;
87.
3 27 90
3 3
2
2
x x
x x
dx
− −
− +
∫
( )( )
;
88.
12 16 3
4 1
2
2
x x
x x
dx
− −
− +
∫
( )( )
;
89.
10 69 74
2 4
2
2
x x
x x
dx
− +
+ −
∫
( )( )
90.
5 53
3 2 2 17
2
x
x x x
dx
+
− + +
∫
( )( )
;
91.
6 23 40
3 2 9 18 13
2
2
x x
x x x
dx
+ +
− + +
∫
( )( )
;
92.
31 64 105
1 16 32 52
2
2
x x
x x x
dx
+ +
− + +
∫
( )( )
;
93.
− − +
+ − +
∫
10 40 70
3 3 8 41
2
2
x x
x x x
dx
( )( )
;
94.
4 29 71
3 8 25
2
2
x x
x x x
dx
+ +
+ + +
∫
( )( )
;
95.
− − −
− + +
∫
35 50 18
2 3 9 18 10
2
2
x x
x x x
dx
( )( )
;
96.
− + −
− − +
∫
6 12 26
2 4 8 25
2
2
x x
x x x
dx
( )( )
;
97.
5 3 46
3 1 6 13
2
2
x x
x x x
dx
− −
+ + +
∫
( )( )
;
98.
2 14 45
3 2 4 16 41
2
2
x x
x x x
dx
+ −
+ − +
∫
( )( )
;
99.
10 2 53
2 1 2 26
2
2
x x
x x x
dx
+ +
+ − +
∫
( )( )
;
100.
− + −
+ − +
∫
62 137 70
2 16 32 20
2
2
x x
x x x
dx
( )( )
.
101.
63 198 310 106
9 36 37
3 2
2 2
x x x
x x
dx
+ + +
+ +
∫
( )
;
102.
− + − +
− +
∫
12 8 31 26
4 8 5
3 2
2 2
x x x
x x
dx
( )
;
103.
− + − +
− +
∫
2 15 90 237
6 25
3 2
2 2
x x x
x x
dx
( )
;
104.
27 105 90
9 18 13
3 2
2 2
x x
x x
dx
− +
− +
∫
( )
;
105.
− − + −
− +
∫
48 48 100 28
16 32 20
3 2
2 2
x x x
x x
dx
( )
;
106.
4 20 24 24
4 8 8
3 2
2 2
x x x
x x
dx
+ + +
+ +
∫
( )
.
107.
− + −
− +
∫
8 28 2
4 16
2
2
x x
x x
dx
;
108.
16 92 78
4 32 48
2
2
x x
x x
dx
− +
− + −
∫
;
109.
− − −
+ +
∫
2 10 12
6 10
2
2
x x
x x
dx
;
110.
54 135 37
9 36 32
2
2
x x
x x
dx
− +
− + −
∫
;
111.
− + −
− + −
∫
16 56 3
4 24 27
2
2
x x
x x
dx
;
112.
− − −
+ +
∫
36 72 53
9 18 18
2
2
x x
x x
dx
;
113.
18 18 31
9 36 35
2
2
x x
x x
dx
− −
− + −
∫
;
114.
− − −
+ +
∫
36 90 34
9 36 37
2
2
x x
x x
dx
;
115.
− − −
− − −
∫
54 180 97
9 36 20
2
2
x x
x x
dx
;
116.
6 24 17
6 8
2
2
x x
x x
dx
+ +
+ +
∫
;
117.
54 162 35
9 36 20
3 2
2
x x x
x x
dx
− +
− + −
∫
;
118.
− − − −
− +
∫
3 28 42
2 17
3 2
2
x x x
x x
dx
;
119.
− + − −
− +
∫
54 234 202 49
9 54 82
3 2
2
x x x
x x
dx
;
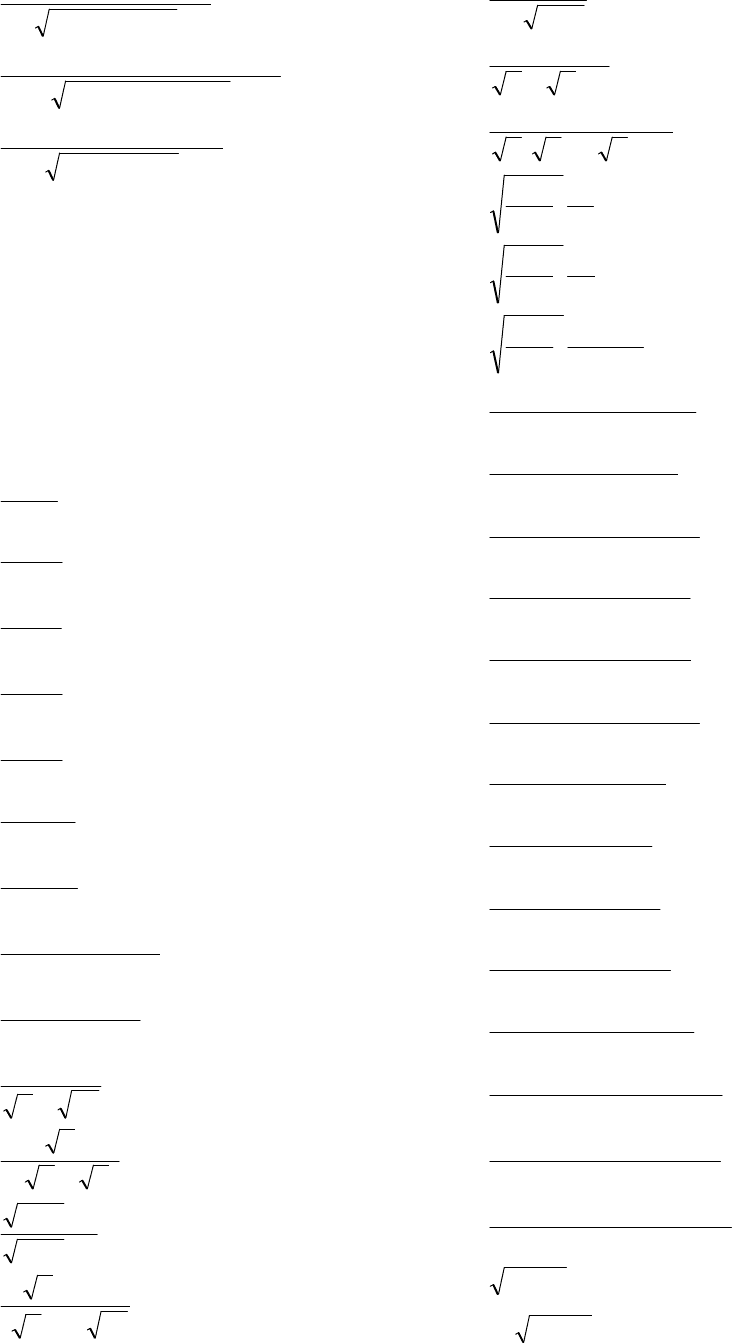
123
120.
− + + +
− + −
∫
6 14 3 2
4 3
3 2
2
x x x
x x
dx
;
121.
− + − +
− + −
∫
54 306 468 191
9 54 72
3 2
2
x x x
x x
dx
;
122.
− + − +
− +
∫
9 47 86 5
6 13
3 2
2
x x x
x x
dx
.
123.
sin cosx xdx⋅
∫
4
.
124.
∫
xdx
2
sin
.
125.
tg xdx
3
∫
.
126.
sin cos
2 3
x xdx⋅
∫
.
127.
sin cos
4 2
x xdx⋅
∫
.
128.
ctg xdx
4
∫
.
129.
dx
x
sin
3
∫
.
130.
dx
x
cos
4
∫
.
131.
cos
sin
3
4
x
x
dx
∫
.
132.
cos
sin
2
4
x
x
dx
∫
.
133.
cos
sin
2
3
x
x
dx
∫
.
134.
dx
ctgx1+
∫
.
135.
ctgx
tg x
dx
1
2
+
∫
.
136.
2 1
2
2
ctgx
x x
dx
+
+
∫
( sin cos )
.
137.
dx
tgx x( ) sin+
∫
1 2
138.
dx
x x+
∫
2
3
.
139.
x
x x x
dx
3
3
( )+
∫
.
140.
x
x
dx
+ −
+ +
∫
1 1
1 1
.
141.
( )
( )
x dx
x x
4
34
1
4
+
+
∫
.
142.
dx
x1 1
3
+ +
∫
.
143.
dx
x x+ +
∫
4
1
.
144.
dx
x x x( )− +
∫
2 2
4
.
145.
1
1
−
+
⋅
∫
x
x
dx
x
.
146.
1
2
+
⋅
∫
x
x
dx
x
.
147.
1
1
2
+
⋅
+
∫
x
x
dx
x( )
.
148.
3
6
8
10
dx
x
x
− − +
∫
sin
cos
;
149.
dx
x
x
6
8
10
sin
cos
+ +
∫
;
150.
dx
x
x
12
51
53
sin
cos
+ +
∫
;
151.
dx
x
x
6
12
14
sin
cos
+ +
∫
;
152.
dx
x
x
16
28
4
sin
cos
− +
∫
;
153.
dx
x
x
10
15
17
sin
cos
+ +
∫
;
154.
dx
x
x
2
5
5
sin
cos
+ +
∫
;
155.
dx
x
x
sin
cos
− −
∫
3
3
;
156.
−
−
+ +
∫
5 15
3
1
sin cos
sin
cos
x x
x
x
dx
;
157.
−
−
−
− −
∫
sin cos
sin
cos
x x
x
x
dx
8 3
2
2
;
158.
−
+
−
+ +
∫
18 14
3
2
2
sin cos
sin
cos
x x
x
x
dx
;
159.
−
−
+
+ −
∫
90 32 86
3 7 7
2
sin cos
( sin cos )
x x
x x
dx
;
160.
−
−
+
+ −
∫
35 38 50
3 3
2
sin cos
(sin cos )
x x
x x
dx
;
161.
−
+
−
− +
∫
16 122 58
4 6 6
2
sin cos
( sin cos )
x x
x x
dx
.
162.
9
2
−
∫
x dx
.
163.
x x dx
2 2
4 −
∫
.
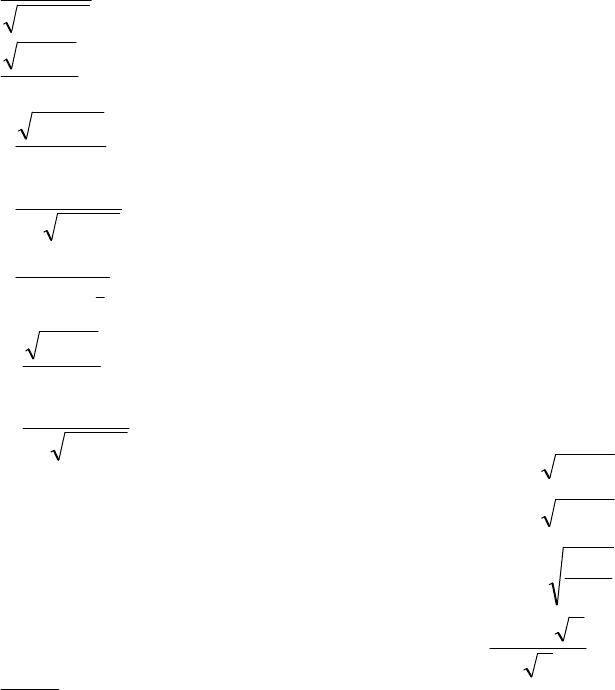
124
164.
x dx
x
2
2
16 −
∫
.
165.
x
x
dx
2
2
1−
∫
.
166.
x
x
dx
2
4
16−
∫
.
167.
dx
x x
2 2
9−
∫
.
168.
dx
x( )9
2
3
2
+
∫
.
169.
1
2
4
+
∫
x
x
dx
.
170.
dx
x x
2 2
4+
∫
.
171.
x xdxcos
∫
;
172.
x xdx
2
sin
∫
;
173.
( ) cos4 2 2x xdx−
∫
;
174.
( ) sinx xdx+
∫
1 3
2
;
175.
xdx
x
sin
2
∫
;
176.
( )4 3
2
−
−
∫
x e dx
x
;
177.
x dx
x
2
∫
;
178.
( )x e dx
x
2 3
2+
∫
;
179.
sin x e dx
x
⋅
∫
;
180.
arcsin xdx
∫
;
181.
arctgdx
∫
;
182.
x xdx
2
ln
∫
;
183.
x x dxln( )3 1−
∫
;
184.
x xdxln
2
∫
;
185.
x xdxarccos
∫
;
186.
x arctgxdx
2
∫
;
187.
arctg x dx2 1−
∫
;
188.
arctg x dx
2
1−
∫
;
189.
arcsin
x
x
dx
+
∫
1
;
190.
arccos x
x
dx
∫
4.5 Определенный интеграл
Пусть функция
)(xfу
=
определена на отрезке
[
]
ba, ,
b
a
<
. Разобьем
этот отрезок на
n
частичных отрезков точками
bxxxxa
n
=
<
<
<
<
=
....
210
. В каждом из полученных частичных отрезков
[
]
ii
xx ,
1
−
выберем произвольную точку
)(
1
iiii
xx
≤
≤
−
ξ
ξ
Сумма
( )
i
n
i
i
xfS ∆=
∑
=
1
ξ
- называется интегральной суммой для функции
)(xf
на отрезке
[
]
ba,
. Предел интегральной суммы
S
при 0max
→
∆
i
x , который
не зависит ни от способа разбиения отрезка
[
]
ba,
на частичные отрезки,
ни от выбора точек в них, называется определенным интегралом
от функции
)(xf
на отрезке
[
]
ba,
и обозначается
( )
i
n
i
i
x
b
a
xfdxxf
i
∆=
∑
∫
=
→∆
)(lim
1
0max
ξ
.
Свойства определённого интеграла.
125
1.
( )
0=∫ dxõf
à
à
,
2.
( )
dxxfdxxf
a
b
b
a
)(∫−=∫ ,
3.
( )
dxxfdxxfdxxf
b
c
c
a
b
a
)()( ∫+∫=∫ ,
4.
( )
dxxgdxxfdxxgxf
b
a
b
a
b
a
)()()]([ ∫±∫=±∫
,
5.
( )
dxxfkdxxfk
b
a
b
a
)(∫⋅=⋅∫
,
6. если
],[ bax
∈
∀
Mxfm
≤
≤
)(
, то
∫
−≤≤−
b
a
abMdxxfabm )()()(
.
Формула Ньютона- Лейбница.
Если функция
)(xfу
=
непрерывна на отрезке [a,b] и функция
)(xF
является некоторой ее первообразной на этом отрезке, то имеет место
формула Ньютона-
Лейбница
( ) ( ) ( )
b
a
b
à
xFaFbFdxõf =−=∫ )(
.
Пример 1
. Вычислить интегралы
dxõ
3
1
0
∫
,
xdxsin
0
π
∫
.
а)
;
4
1
4
1
1
0
43
1
0
==∫ xdxõ
б)
20coscos
0
cossin
0
=+−=−=∫
π
π
π
xxdx
.
Пример 2.
Вычислить интеграл dxxx )
3
2(
8
0
+∫ .
.
3
1
3312
3
64
8
0
3
4
4
3
8
0
2
3
3
2
2
3
2
8
0
)
3
2(
8
0
=+=+⋅=
∫
+∫=+∫ xxdxxdxxdxxx .
Замена переменной.
( )
dtttfdxxf
b
a
)()]([
ϕϕ
β
α
′
∫=∫ ,
где
)(tx
ϕ
=
- функция непрерывная вместе со своей производной
)(t
ϕ
′
на
отрезке
β
α
≤
≤
t
,
)]([),(),( tfba
ϕβϕαϕ
==
- функция непрерывная на
],[
β
α
.

126
Пример 3.
Вычислить интеграл
(
)
dxxx
5
2
2
1
0
−∫ .
( )
12
3
5
6
1
2
1
2
1
.1,2
,1,0
,
2
,2
,2
2
1
2
65
1
2
2
5
2
1
0
=⋅−=∫−=
==
==
=−
−=
−=
=−∫ tdtt
ba
xdx
dt
xdxdt
xt
dxxx
βα
.
Интегрирование по частям.
Если
)(,)( xvvxuu ==
- непрерывно дифференцируемые функции на
отрезке [a,b], то
∫∫
−=
b
a
vdu
b
a
b
a
uvudv .
Пример 4.
Вычислить интеграл
dxxe
x
−
∫
1
0
.
e
e
eeedxexe
evdxdu
dxedvxu
dxxe
xxx
x
x
x
2
12
,
,
1
0
1
1
0
1
1
0
1
0
−
=+−=−−=+−=
−==
==
=∫
∫
−−−−−
−
−
−
.
Задачи для самостоятельного решения
.
Вычислить интегралы:
1.
( sin )x
x
x dx−
−
−
∫
1
4
2
0
1
π
.
2.
dx
x
x
x
)
1
4
cos32(
2
1
0
+
++
∫
π
.
3.
( )x
x
x
dx
4
1
2
2
3 2
1
− +
+
∫
.
4.
( ( ) )3
1
3
1
0
3
2 1
− −
+
∫
x x
dx
.
5.
dx
x xsin cos
2 2
4
3
π
π
∫
.
6.
ctg xdx
2
8
4
2
π
π
∫
.
7.
dx
x x
e
1
1
2
+
∫
ln
.
8.
( ( ) )1 2 1
2
0
1
+ + +
∫
x x dx
.
9.
∫
+
−
1
0
))
3
(
24
3
( dx
x
tg
x
π
.
10.
1
9
0
16
x x
dx
+ −
∫
.
__________________
127
11.
x xdxcos
0
2
π
∫
.
12.
xe dx
x
0
1
∫
.
13.
ln xdx
e
1
∫
.
14.
x xdx
2
0
sin
π
∫
.
15.
x xdxln
1
10
∫
.
16.
x xdxln
2
1
2
∫
.
17.
arctgxdx
0
1
∫
.
18.
arcsin
,
xdx
0
0 5
∫
.
19.
e xdx
x
2
0
2
cos
π
∫
.
20.
4
2
0
2
−
∫
x dx
.
__________________
21.
dx
x x+
∫
2
1
2
.
22.
dx
x x2 3 2
2
2
3
+ −
∫
.
23.
xdx
x x( )( )− −
−
−
∫
1 2
2
1
.
24.
x
x x
dx
3
2
2
3
1+
−
∫
.
25.
x x
x x x
dx
3 2
0 5
1
2 3
4 2
+ +
− −
∫
( )( )
,
.
26.
4 19 19
1 2 3
2
1
0
x x
x x x
dx
− +
− − −
−
∫
( )( )( )
.
27.
dx
x x
3
1
2
+
∫
.
28.
x x
x
dx
2
3
2
0
3 1
1
+ −
−
−
∫
.
29.
x x
x x x
dx
2
2
0
1
1
1 2 2
− −
+ + +
∫
( )( )
.
30.
x
x x x
dx
+
+ +
∫
1
3 2
1
2
.
__________________
31.
dx
x1
2
2
+
−
∫
cos
π
π
32.
tg x
x
dx
( )
cos ( )
+
+
−
∫
1
1
2
1
0
.
33.
cos sin
5
0
2
2x xdx
π
∫
.
34.
cos
sin
3
3
2
4
x
x
dx
−
−
∫
π
π
.
35.
ctg xdx
4
6
4
π
π
∫
.
36.
sin cos
2 4
0
x xdx
π
∫
.
37.
cos
cos
x
x
dx
2
0
2
+
∫
π
.
38.
dx
x x
arctg
sin ( cos )
2
2
2 2
1 −
∫
π
.
39.
cos
sin cos
xdx
x x1
3
2
+ −
∫
π
π
.
40.
4 7
2 3
0
4
−
+
∫
tgx
tgx
dx
π
.
_______________
41.
dx
x x8 2
2
0 5
1
+ −
−
∫
,
.
42.
dx
x x+
∫
1
4
.
43.
xdx
x
3
0
1
1+
∫
.

128
44.
1 2
2
6 3
3 43
1
64
− +
+ +
∫
x x
x x x
dx
.
45.
( )
( )
2
2
3
6 3
1
64
+
+ +
∫
x
x x x x
dx
.
46.
x x dx
2 2
0
1
1 −
∫
.
47.
x
x
dx
2
4
1
2
1−
∫
.
48.
dx
x( )1
2 3
1
3
+
∫
.
49.
x x
x
dx
+ − −
− +
∫
3 2 10
3 2 7
1
2
.
50.
dx
x( )16
2 3
0
2
−
∫
.
4.6 Приложения определенного интеграла.
Вычисление площадей плоских фигур.
1.
Площадь криволинейной трапеции ограниченной линиями
)(xfу
=
,
0 , ,
=
=
=
ybxax
, расположенной выше оси Ох (
0)(
≥
xf
), равна :
S
( )
dxxf
b
a
∫= .
Пример 1.
Найти площадь плоской фигуры ограниченной параболой
2
2 xxy −= и осью Ох.
Парабола пересекает ось Ох в точках О(0;0) и М(2;0), следовательно
будем иметь
3
4
3
8
4
3
1
)2(
2
0
322
2
0
=−=
−=−∫= xxdxxxS .
2.
Если криволинейная трапеция расположена ниже оси Ох (
0)(
≤
xf
), то
ее площадь может быть найдена по формуле
S
( )
dxxf
b
a
∫−=
.
3
.
Пусть на отрезке
[
]
bа; заданны и непрерывны функции
);(
1
xfу
=
(
)
xfy
2
=
такие, что
(
)
xf
2
)(
1
xf
≥
. Площадь фигуры
S
, ограниченной кривыми
)(
1
xf
,
(
)
xf
2
, и прямыми
, , bxax
=
=
вычисляется по формуле:
S
( )
dxxfdxxf
b
a
b
а
12
)( ∫−∫= .
Пример 2.
Найти площадь фигуры, ограниченной гиперболой
х
у
1
= и прямыми
;
x
y
=
.2
=
x
Гипербола пересекает прямую
x
y
=
в точке М(1;1) и
[
]
2;1∈∀
x
выполняется неравенство
x
x
≤
1
, поэтому площадь фигуры, образованной
линиями будет равна
129
.2
2
3
02
2
1
2
4
2
1
,
1
2
1
2
1
2
2
1
2
1
nnnxxdx
x
xdxS lll −=+−−=−=∫−∫=
4.
Площадь криволинейной трапеции, верхняя граница которой задана
параметрическими уравнениями
=
=
),(
),(
ty
tx
ψ
ϕ
β
α
≤
≤
t
, вычисляется по формуле:
S
dttt )()(
ϕψ
β
α
′
∫= .
Пример 3.
Вычислить площадь фигуры, ограниченной эллипсом
.sin,cos tbytax ==
Найдем сначала площадь верхней половины фигуры, ограниченной
эллипсом. При возрастании x от -a до a параметр t убывает от
π
до 0.
Находим
22
2sin
2
)2cos1(
2
sin)sin(sin5,0
0
0
2
00
abt
t
ab
dtt
ab
tdtabdttatbS
π
π
πππ
=
−−=−∫−=∫−=−⋅∫=
.
Таким образом
2
5,0
ab
S
π
=⋅
. Значит,
abS
π
=
.
5. Площадь криволинейного сектора, ограниченного кривой, заданной в
полярных координатах уравнением
,
),
(
β
ϕ
α
ϕ
ρ
ρ
≤
≤
=
и двумя
полярными радиусами, составляющими с полярной осью углы
α
и
β
,
вычисляется по формуле:
S
.)(
2
1
2
ϕϕρ
β
α
d∫=
Пример 4.
Найти площадь фигуры, ограниченной кардиоидой
)cos1(
ϕ
ρ
+
⋅
=
a
.
.
2
3
2
2sin
84
sin
22
2cos1
2
cos
2
)cos1(
2
22
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
2
0
2
aa
a
aa
a
a
d
a
dad
a
d
a
S
ππ
πϕϕ
ϕϕϕ
ϕ
ϕϕϕϕϕ
ππ
ππ
ππππ
=+=++
++=
+
∫+∫+∫=+∫=
Формулы длин дуг плоских кривых.
1.
Длина
L
кривой, заданной уравнением
)(xfу
=
,
b
x
a
≤
≤
вычисляется
по формуле:
( )
dxxfL
b
a
2
1
′
+∫= .

130
Пример 5.
Найти длину дуги кривой
32
xó =
от
0
=
x
до
4
=
x
.
Кривая симметрична относительно оси Ox. Найдем длину верхней ветви
кривой. Из уравнения
2
3
xу = находим
2
1
2
3
xу =
′
. По формуле вычисления
длины дуги получим
( )
27
8
4
9
11
2
1
4
0
2
4
0
=+∫=
′
+∫= dx
x
dxxfL
( )
.11010
27
8
4
9
1
4
0
2
3
−=
+
x
Тогда длина всей кривой будет
(
)
.11010
27
16
−=L
2
.
Длина
L
кривой заданной параметрическими уравнениями
=
=
),(
),(
ty
tx
ψ
ϕ
β
α
≤
≤
t
, вычисляется по формуле:
( )
dtttL
22
)(
ψϕ
β
α
′
+
′
∫=
Пример 6.
Найти длину дуги окружности taytax sin,cos
=
=
от t=0 до t=T.
Из параметрических уравнений окружности находим
taytax
cos,sin =
′
−=
′
. По формуле вычисления длины дуги получим
( ) ( )
.cos)sin()(
0
0
2
2
0
22
0
aTatadtdttatadttytxL
T
TTT
==∫=+−∫=
′
+
′
∫=
3
0
Длина
L
кривой заданной в полярных координатах уравнением
,
),
(
β
ϕ
α
ϕ
ρ
ρ
≤
≤
=
вычисляется по формуле:
( )
ϕϕρϕρ
dL
b
a
2
)(
′
+∫= .
Пример 7.
Найти длину кардиоиды
)cos1(
ϕ
ρ
+
⋅
=
a
.
Из уравнения кардиоиды находим
ϕ
ρ
sin
⋅
−
=
′
a
. Кардиоида симметрична
полярной оси. Найдем половину длины этой линии
( ) ( )
.4
2
sin4
2
cos2
2
cos22
cos22)sin()cos1()(
2
1
0
0
2
0
0
2
2
0
22
0
aadada
dadaadL
===⋅∫=
=+∫=−+∫=
′
+∫=
∫
π
π
π
πππ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕϕϕϕϕϕϕρϕρ
Таким образом
aL 4
2
1
=
. Отсюда находим длину кардиоиды
aL 8
=
.
