Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

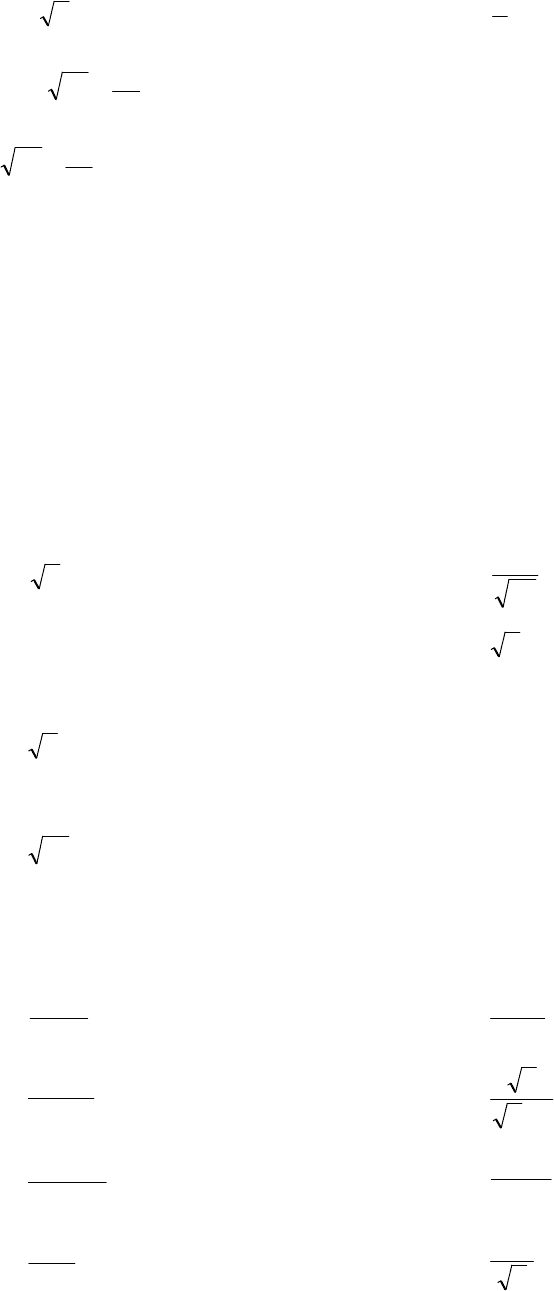
91
31. у = xx sin23
−
32. у = tg x x 37
2
+
33. у =
xx -x ctgcos23
3
+
34. у = x x x tg2sin3
4
1
4
++
35. у =
x xx
x
x
2
2
5
3
log3cos7sin
3
42 −+−++
36. у =
x x x
x
x ln4sin3cos2
1
3
3
2
+−+−
37. у =
xx
53
log4log2 +− 38. у = x xx- lg2log
7
+
39.
xxe
x
cos2ln2y +−= 40. xx
x
tg3log10y
2
+−=
41.
xx
x
sin6ctg23y +−= 42. x
x
coslnx7y −+=
43.
xx arcctg3arcsin2y
+
=
44. 1arccos4arctg7y
+
−
=
xx
45.
xxex
x
sinlg3arctg4y +−+= 46. xxx
x
sin610lnarcsiny −+−=
47.
x
xx 107logarctg3y
3
×+−=
48. xxx
x
lg2arctg3tg2y +−−=
49.
x
xxx 8arctgln6y
3
++−=
50.
xx
x
x
ln23arcsin2
2
y
5 4
−−−=
51.
xx siny
=
52. xx lny
3
⋅=
53.
x
x 10y
3
⋅=
54.
x
x
arccos
y
=
55.
xx arctgy ⋅=
56.
x
x 10y
3
⋅=
57. xx lny
4
= 58. xx lgy
3
⋅=
59.
xx tgy
5
4
⋅=
60. x
x
ctg2y ⋅=
61. xxx lncosy
⋅
⋅
=
62. xxx arctgsiny
⋅
⋅
=
63. xx
x
arcsintg2y ⋅⋅= 64. )(logctgy
2
xxe
x
⋅⋅=
65.
1
1
y
2
2
+
−
=
x
x
66.
3
3
1
1
y
x
x
−
+
=
67.
x
x
cos
1ln
y
+
=
68.
1
y
+
=
x
x
69.
x
xarccos
y =
70.
x
x
2
log
1
y
−
=
71.
2
sin
y
x
x
=
72.
x
xctg
y =
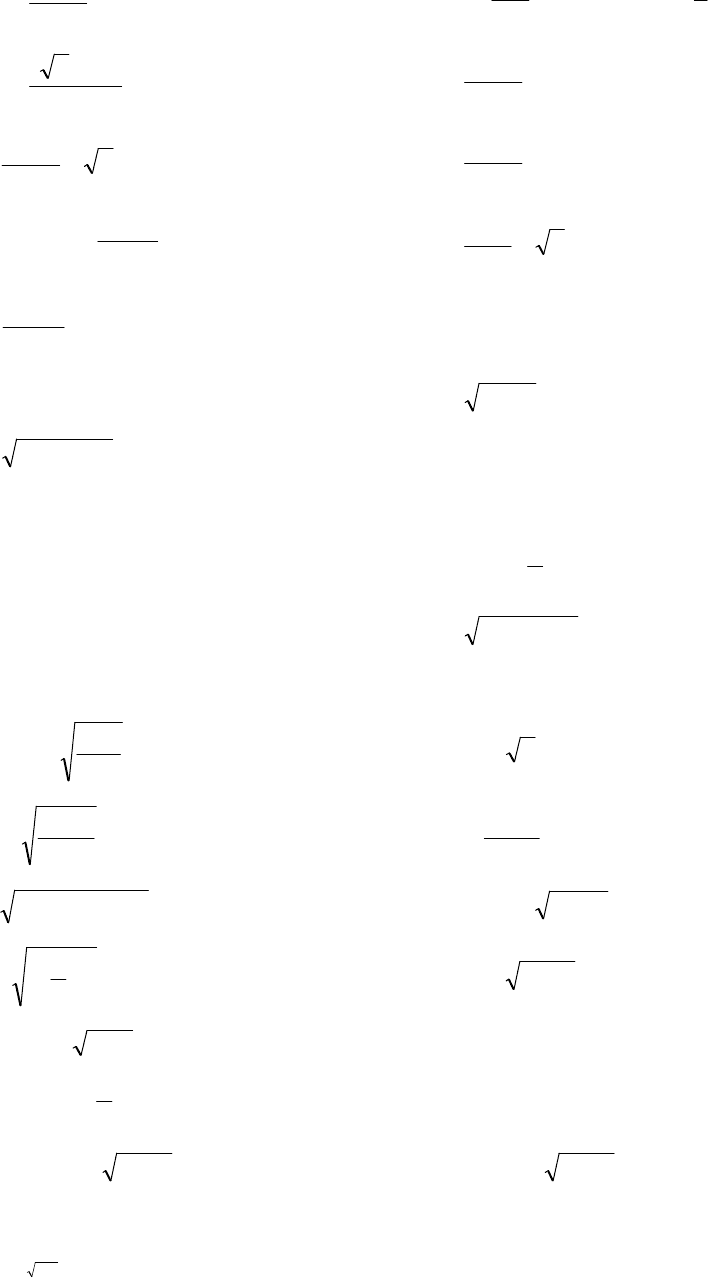
92
73. (0)f найти ,
2
1
21
)(f
′
+
−
=
x
x
x
74.
( )
3
f,
1
f ),(f найти ,
ln
)(f e
e
e
x
x
x
′
′′
=
75.
,1)0(f0,1 найти ,
)1(
)(f
2
′
⋅
+
=
x
x
x
76.
xx
x
x
tg
1
ln
y
2
⋅−
+
=
77.
xx
x
e
x
arcsin
1
y
2
⋅+
+
=
78.
x
ex
x
x
⋅+
+
=
2
1
y
79.
x
x
xx
3
log
1
cosy
−
+⋅=
80.
xx
x
e
x
lg
sin
y
5
+=
81.
x
x
x
x
ln2
arctg
y
2
⋅⋅=
82. x
2
cosy =
83. x
3
siny =
84.
2
1y x−=
85.
xx cosy
3
+=
86. )3(tgy
2
+= x
87. xcoslny
=
88. xsinlny
=
89. x5tglny
=
80.
x
1
arctgy
2
=
91. x2arccoslny
=
92.
x3sin1y
3
+=
93.
5
)5tg1(y x+= 94.
3
)sinln1(y x+=
95.
x
x
+
−
=
1
1
arcsiny
96. xlnlny =
97.
x
x
21
21
lny
−
+
=
98.
2
2
1
1
lny
x
x
−
+
=
99.
2
)(arccos1y x−=
100. )5ln(y
2
++= xx
101.
1
2
tgy +=
x
102.
2
1siny x+=
103.
xsinarcsiny =
104. )arcsin(y
4 x
e=
105.
2
2
arccosy
x
e
−
=
106. )35ln(arctgy
+
=
x
107.
)1(arctgy
2
xx +−= 108.
2
1arctglny x+=
109. xcossintgy
=
110.
x
e
2arcsin
y =
111.
x
ey
ln
=
112.
x
3
sin
3y =
113.
x2cos3
3
10y
−
=
114. )2(siny
cos x
⋅=
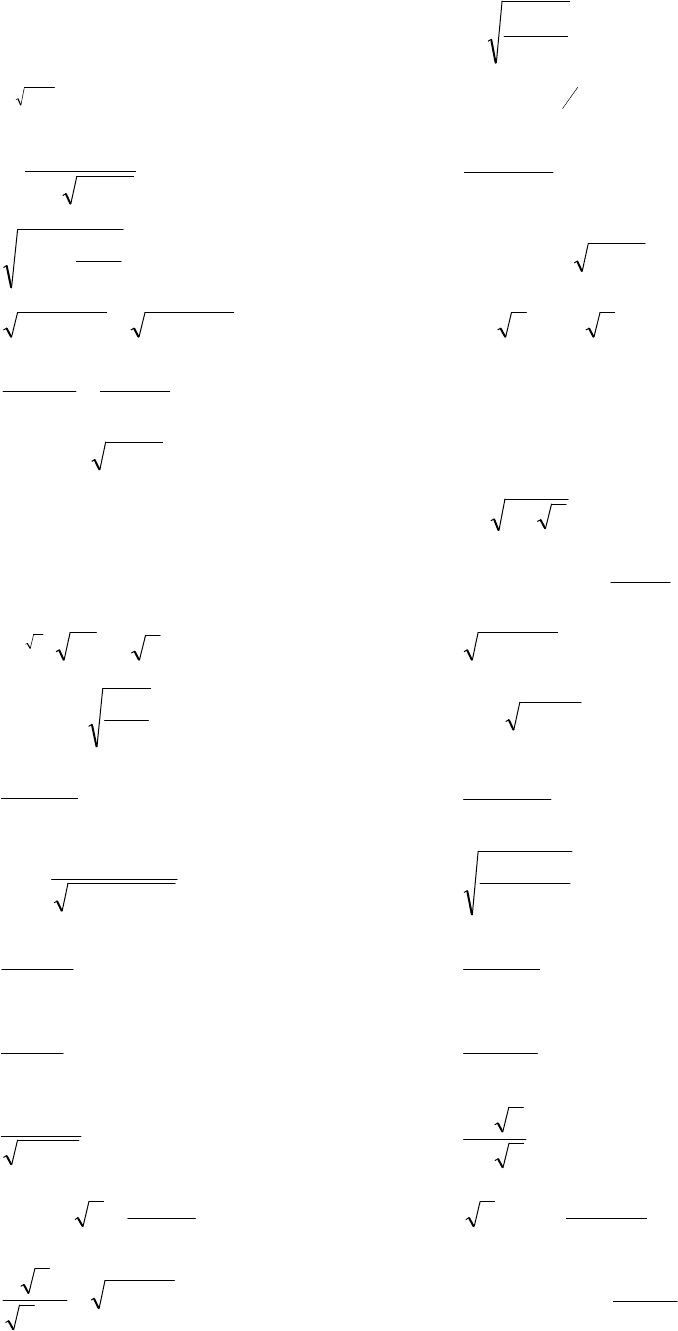
93
115.
)cos(y
23
2
−+
=
xx
e
116.
1
lny
2
2
+
=
x
x
e
e
117.
3
4
1 x
ey
−
=
118.
4
tgcoslgy
x
e
−
=
119.
1
1
lny
2
−+
=
xx
120.
x
e
2
arctg
1
y
−
=
121.
5
2
1
coslny
−
=
x
122.
22
1arcsiny xx −+=
123.
xx 2sin12sin1y −−+= 124.
44
cossiny xx +=
125.
x
x
3
sin
1
3
cos
1
y
22
+=
126. )arccos(lny xx
=
127.
22
1arcsiny xx −=
128.
x
ex
sin
cosy ⋅=
129. xx 2cos)(lgy
=
130.
xx += 1y
2
131.
x
xe
tg1
y
−
=
132.
3
2
1
arcsin)32(y
4
+
+=
x
x
133.
)22(2y
3
3
2
+−= xxe
x
134. xx 7arctg149y
2
⋅+=
135.
1
arccosy
+
⋅=
x
x
x
136.
xx
ee
42
1y +⋅=
137.
x
xx
2tg1
2sin
y
+
=
138.
x
x
2
sin
1
2sin1
y
−
+
=
139.
4cos9
sin2
arctgy
2
−
=
x
x
140.
x
x
arctg1
arctg1
y
+
−
=
141.
x
x
cos
ln
sinln
y =
142.
x
x
ctg1
sin
y
2
+
=
143.
x
x
tg1
cos
y
2
+
=
144.
x
x
2
2
tg1
tg1
y
+
−
=
145.
x
x
2cos
cos2
y =
146.
2
3
3
sin
1
1
y xx
x
x
+
+
−
=
147.
x
x
xx
ln
1
ln1
arctgy
2
+
−
+= 148.
x
x
xx
cos
1
cos1
lny
+
−
−⋅=
149.
xx
x
x
2arcsin41
1
y
2
−−
+
=
150.
x
x
e
e
xx
2
2
22
1
1
sinsiny
−
+
+⋅=
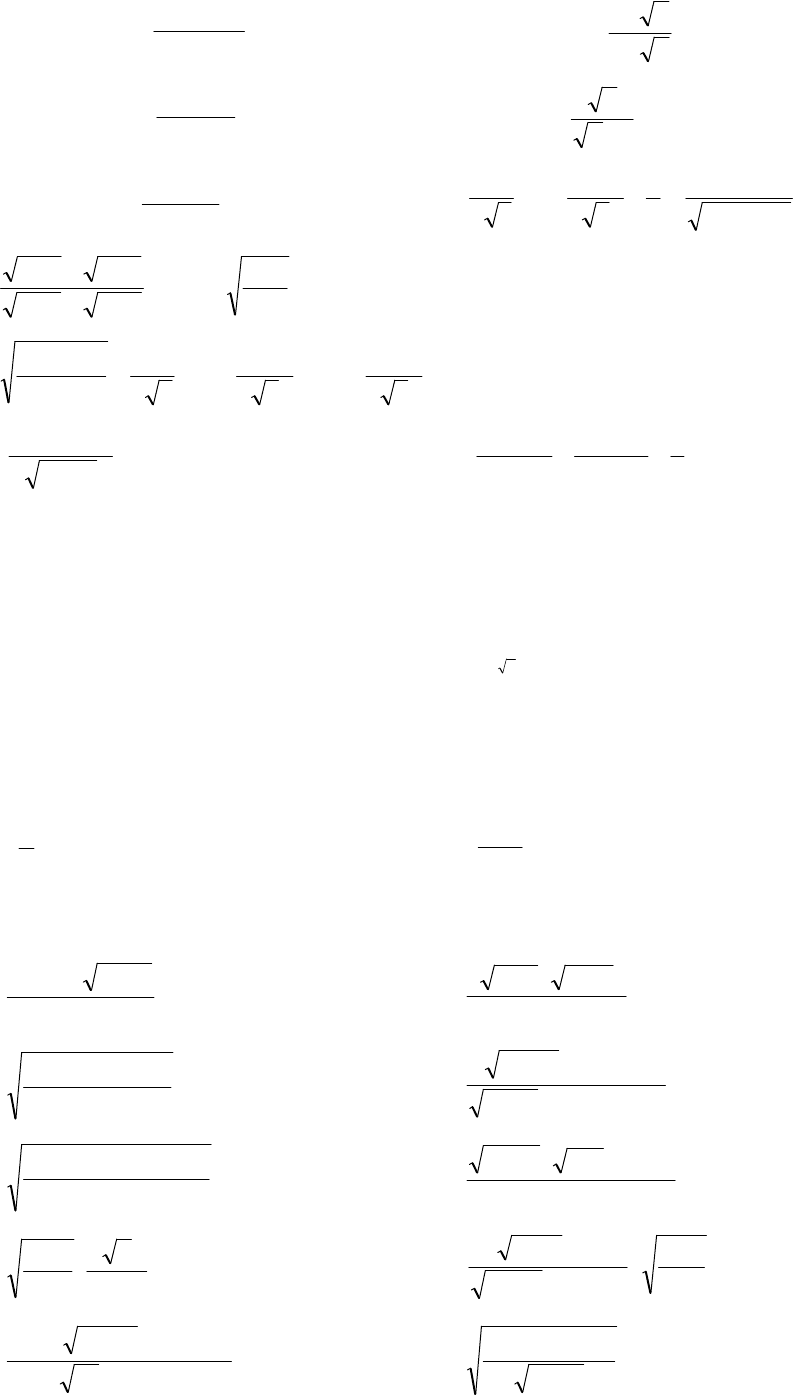
94
151.
x
x
xx
2
cos
1
2tg
)(arcsin4y
2
+
+=
152.
x
x
xx
+
−
+⋅=
1
1
arcsin3y
3
153.
x
x
xx
cos
1
sin
arctg)1(y
2
+
++=
154.
1
lny
22
−
−⋅=
x
x
xx
155.
x
xx
e
ee
xx
+
−
−⋅=
−
1
2cossiny
156.
1
1
ln
6
1
3
12
arctg
32
1
y
2
+−
+
+
−
=
xx
xx
157.
x
x
xx
xx
+
−
+
+++
−−+
=
1
1
arctg2
11
11
lny
158.
)
3
12
arctg
3
12
arctg(
32
1
1
1
lny
4
2
2
−
+
+
+
+−
++
=
xx
xx
xx
159.
)1ln(
1
arctg1
y
24
2
2
++
+
+
=
−
xe
x
xx
x
;
160.
8
3
cos
8
sin3
cos
4
sin
y
24
++=
x
x
x
x
3. Найти производные у′ данных функций, используя правило
логарифмического дифференцирования.
161.
x
x
sin
)(lny =
162.
x
x)(y =
163.
x
x
tg
)1(y += 164.
x
x
cos
)(siny =
165.
)1(2
)(y
+
−=
x
xx 166.
x
x)ctg(y =
167.
2
1
y
x
x
=
168.
x
x
x
+
=
1
y
169.
x
xx
2
2
sin
)(y +=
170.
x
x
ctg
)2tg(y =
171.
3
3
22
)3(
1 )1(
y
−
−+
=
x
xx
172.
32
3
2
)4()3(
21
y
+⋅+
+⋅−
=
xx
xx
173.
3
32
2
)5)(4(
)1(
y
−+
−
=
xx
xx
174.
)15(1
)3(2
y
2
3
3
10
7
2
++⋅+
−⋅+
=
xxx
xx
175.
5
3
)2)(arctg1(
)1()arctg1(
y
++
−⋅−
=
xx
xx
176.
732
2
3
3
)5()1(
coslnsin
y
+⋅−⋅
⋅⋅
=
xxx
xxx
177.
42
1
y
2
3
+
⋅
+
−
=
x
x
x
x
178.
1
)1(1
7
y
32
2
3
+
⋅
−⋅+
⋅+
=
x
x
xx
xx
179.
22
3
354
)1(
)17(cos
y
−
+⋅⋅
=
xe
xxxtg
x
180.
5
2
3
1
)3)(1(
y
+
+−
=
x
xx
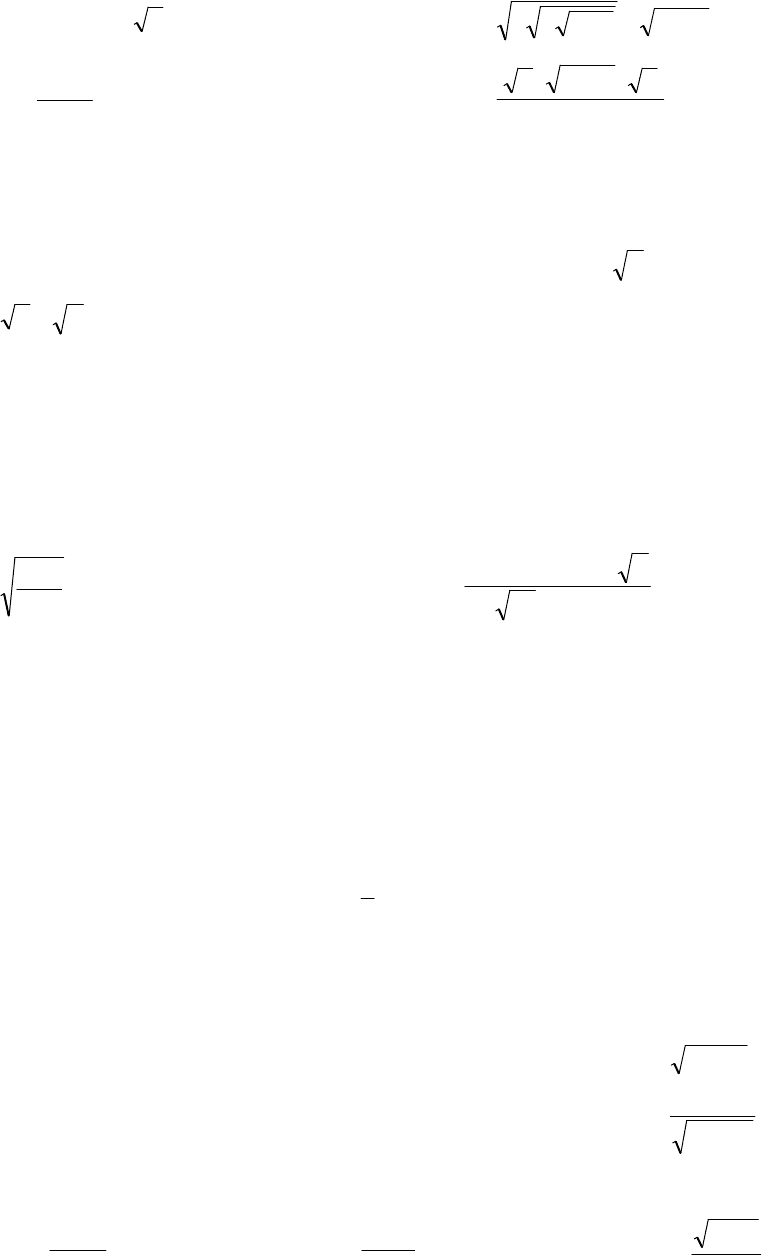
95
181. xxx
x
ln)3ctg(y ⋅−=
182.
xxxxx arcsin11y
23
5
7
⋅−++=
183.
2
)(ln
1
1
y
2
2
x
x
x
x
−
+
−
=
184.
xx
xx
xxx
sin
)4()1(
1
y
7
325
5
3
2
⋅+
+⋅−
⋅−⋅
=
4. Найти производные
х
у
′
и
у
х
′
от функций заданных неявно.
185. 13
33
=−+ уух
186.
0
22
=−⋅−⋅ ухуху
187.
04 =−+ хуух
188. 1
2244
=++ ухух
189. хууx
=
−
arcsinarcsin
190. 0
2
=−⋅ хеу
у
191. 0)(tg)(sin
=
−
+
уx ху 192. xууу cos5sin
+
=
193.
ухуx
еee
=
=+
194.
2
)( arctg ууx =+
195.
2
ln1 хуу =− 196. 0)(ln
22
=⋅−+ ухху
197.
ee
х
у
y
=⋅
+
−
1
1
198.
2
52
32
)4(
)1()1(
e
хху
уху
=
+
+⋅+
199. eхуxууx =−−−
543
)3()2()( 200.
464
)3()2()( eухуxуx =+++
5. Найти производные от у по х от параметрически заданных
функций.
201.
−=
−=
3
2
у
1x
tt
t
202.
−=
=
tt
t
3
2
3
1
у
x
203.
=
=
t
t
2
cosу
tgx
204.
=
=
tв
ta
sinу
cosx
205.
=
=
ta
tа
3
3
sinу
cosx
206.
−=
−=
) cos1(2у
)sin(2x
t
tt
207.
−=
+=
tt
t
arctgу
)1ln(x
2
208.
=
=
tе
tе
t
t
sinу
cosx
209.
−
=
−=
3
2
2
)1(
1
у
2x
t
tt
210.
=
=
t
t
2
cos
1
у
ctglnx
211.
=
=
t
t
2
sin
1
у
tglnx
212.
+
+
=
=
1
1
lnу
arctgx
2
t
t
t
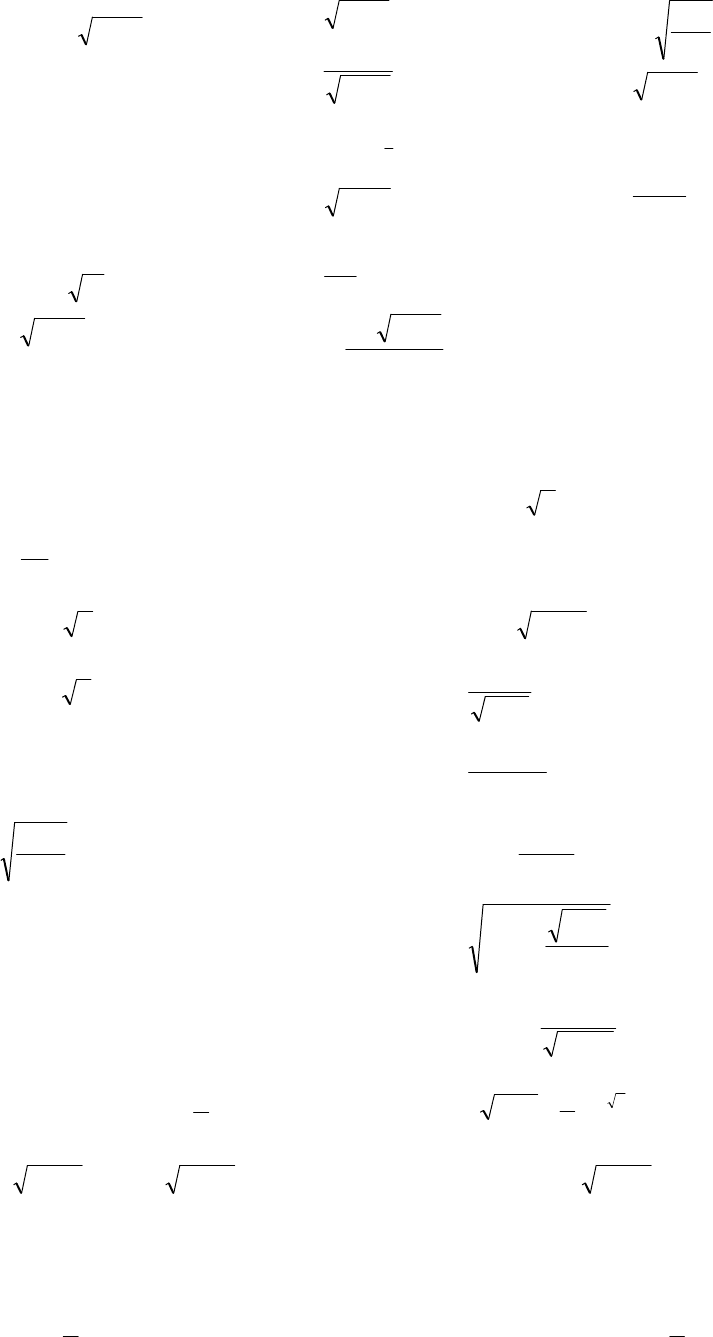
96
213.
=
−=
2
2
)(arccosу
)1arcsin(x
t
t
214.
−
=
−=
2
2
1
у
1x
t
t
t
215.
−=
+
−
=
2
1у
1
1
lnx
t
t
t
216.
=
=
)tgln(у
)2(ctgx
t
t
e
e
217.
+=
=
1у
arctgx
2
t
t
e
e
218.
=
+=
t
t
t
2
22
sin
cos
у
)cos1(x
219.
+=
++=
1у
)1ln(x
2
2
tt
tt
220.
−+
=
=
t
t
t
2
11
lnу
ln
1
x
6. Найти дифференциалы функций
:
221. x3cosy
3
=
222. )ln(siny x=
223.
x
e
sin
1
y
−
=
224.
2
10y
x
−
=
225.
xarccosy =
226.
1arctgy
2
+= x
227.
xx cosy
2
=
228.
1
1
y
+
+
=
x
x
229.
x
arctg
x
y
=
230.
x
x
cos
1
sin
y
−
=
231.
3
2
2
y
−
+
=
x
x
232.
x
x 1
arctgy
2
−
=
233. )cos2ln(siny xxx
+
−
=
234.
3
tg
ctgy
3
x
x −=
235. x3cosy
3
=
236.
+
=
x21
1
arccosy
237.
)
2
tgln()tgln(cosy
x
xx −⋅=
238.
12
2
1
1y
−
−−=
x
ex
239.
)1ln(1y
22
+++−= xxxx 240.
2
1lnarctgy xxx +−=
7. Найти производные второго порядка от функций:
241.
2
arccosy
x
=
242.
x
ctg
y
=
243.
2
siny
2
x
=

97
244.
x
1
arctgy =
245.
2
1y x+=
246.
1
1
y
+
−
=
x
x
247.
)1ln(y
2
xx ++= 248. xx arcsin1y
2
−=
249.
3
ln
y
x
x
=
250.
x
x=y
8. Найти производные третьего порядка от функций:
251. x
2
cosy = 252.
6
)2(y += x
253.
2
arctgy
x
=
254. xx siny
2
= 255.
x
ex
3
y = 256. xe
x
cosy =
257.
)2cos32(siny xxe
x
−=
−
258. xx lny
3
=
259.
x
x2sin
y =
260. xx arctg)1(y
2
+=
9. Найти общие выражения для производных порядка n от функций:
261.
x
3
2y =
262.
2
y
x
e=
263. x
2
siny =
264.
n
x )12(y +=
265.
x
4
y = 266.
1
y
−
=
x
x
267.
x
xe=y
268. )72lg(y
+
=
x 269.
x
x
cos
y
=
270. xx lny
2
=
10. Найти вторые производные у″
хх
от функций, заданных неявно:
271. 03
=
+
+
ух
272. 1=
y
х
273.
222
ayx =+
274.
233
ayx
=
+
275. уxe
y
=+1
276. )sin( yxy
+
=
277. 03
33
=++ axyyx
278.
yx
exy
+
=
279.
y
x
y
+
=
arctg
280. )(ctg yxу
−
=
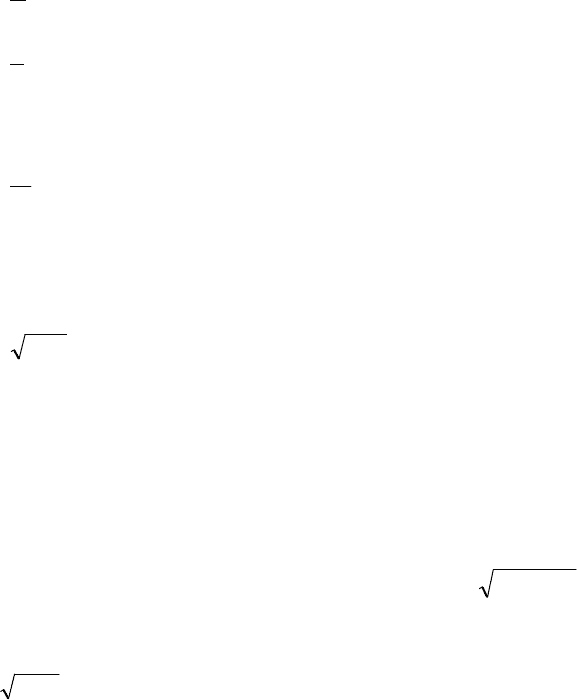
98
11. Найти вторые производные у″
хх
от функций, заданных
параметрически:
281.
=
=
3
2
3
1
у
2
1
x
t
t
282.
=
=
t
t
cos5у
sin5x
283.
=
=
tb
ta
sinу
cosx
284.
−=
=
t
t
t
3
у
x
3
2
285.
−=
−=
)cos1(y
)sin(x
ta
ttа
286.
=
=
ta
t
3
3
sinу
cosx
287.
+=
=
tt
t
3
2
у
x
288.
=
=
tе
tе
t
t
sinу
cosx
289.
=
=
t
t
2
2
tgу
cosx
290.
−=
−=
)2ln(у
3x
t
t
12. Найти дифференциалы указанных порядков от функций:
291. y найти ;353y
224
dxx +−=
292.
y найти ;5y
2
2
d
x
−
=
293.
y найти ;5y
2
2
d
x
−
=
294. y найти ;9lny
22
dx −=
295. y найти ;cosy
32
dx= 296. y найти ;y
43
de
x
=
297.
y найти ;1y
4
dx −=
298. y найти ;lny
5
dxx=
299. y найти ;siny
5
dxx= 300. y найти );1lg(y
10
dx +=
4.3. Приложения производной.
Возрастание и убывание функции.
Функция
)(xfy
=
называется возрастающей (убывающей) на отрезке
],[ ba
, если
)()(
12
xfxf >
при
bxxa ≤<≤
21
(или соответственно
)()(
12
xfxf <
при
bxxa ≤<≤
21
).
Необходимый признак возрастания (убывания) функции на отрезке
],[ ba
.
Если дифференцируемая функция
)(xfy
=
возрастает (убывает) на
отрезке
],[ ba
, то
0)(
≥
′
xf
при
bxa
≤
≤
(или
0)(
≤
′
xf
при
bxa
≤
≤
).
Достаточный признак возрастания (убывания) функции.
Если функция
)(xfy
=
непрерывна на отрезке
],[ ba
и внутри него
имеет положительную (отрицательную) производную
)(xf
′
, то функция
)(xfy
=
возрастает (убывает) на отрезке
],[ ba
.
99
Направление вогнутости, выпуклости графика функции. Точки
перегиба.
График дифференцируемой функции
)(xfy
=
называется выпуклым
(вогнутым) на отрезке
],[ ba
, если отрезок кривой
)(xfy
=
(
bxa
≤
≤
)
расположен ниже (соответственно выше) касательной, проведенной к
кривой в любой точке этого отрезка. Достаточным условием вогнутости
(выпуклости) графика функции, в предложении существования второй
производной
)(xf
′
′
, является выполнение неравенства
)0)((0)(
<
′
′
>
′
′
xfxf
при
bxa
<
<
.
Точка, в которой меняется направление вогнутости графика
функции, называется точкой перегиба. Точка
0
x
, для которой
0)(
0
=
′
′
xf
,
либо
)(
0
xf
′
′
не существует, есть точка перегиба, если
)(xf
′
′
меняет свой
знак при переходе через значение
0
x
.
Экстремум функции.
Точка
0
x
называется точкой экстремума (максимум или минимум),
если функция
)(xfy
=
определена в двухсторонней окрестности точки
0
x
и
для всех точек
x
некоторой области:
δ
<−<
0
0 xx
, выполнено
соответственно неравенство
)()(
0
xfxf <
или
)()(
0
xfxf >
соответственно.
Необходимые условия экстремума.
В точке экстремума
0
x
производная функции
)(
0
xf
′
либо равна нулю,
либо не существует.
Достаточное условие экстремума.
Пусть функция
)(xfy
=
определена и непрерывна в некоторой
окрестности
δ
<−
0
xx
точки
0
x
такой, что
0)(
0
=
′
xf
или не существует
(критическая точка); имеет конечную производную
)(xf
′
в области
δ
<−<
0
0 xx
. Тогда, если при переходе через точку
0
x
производная
)(xf
′
меняет знак с «+» на «-», то точка
0
x
будет точкой максимума. Если при
переходе через точку
0
x
производная
)(xf
′
меняет знак с «-» на «+», то
точка
0
x
будет точкой минимума.
Наибольшее и наименьшее значения функции на отрезке.
Теорема. Наименьшее (наибольшее) значение непрерывной функции
)
(
x
f
y
=
на данном замкнутом отрезке
]
,
[
b
a
достигается или в
критических точках, лежащих внутри отрезка
]
,
[
b
a
(т.е. в точках, где
производная функции )(xf
′
либо равна нулю, либо не существует), или на
концах отрезка
]
,
[
b
a
.
Исследование и построение графика функции.
Построение графика функции
)
(
x
f
y
=
может быть осуществлено
после исследования, которое проводится по следующему плану:
1.
Область определения функции.
100
2.
Область непрерывности функции. Точки разрыва (если они
имеются). Исследование поведения функции в окрестности точек
разрыва 2-ого рода (вертикальные асимптоты).
3.
Четность, нечетность, периодичность, непериодичность функции.
4.
Монотонность функции (нахождение участков возрастания,
убывания).
5.
Точки экстремума.
6.
Выпуклость, вогнутость.
7.
Точки перегиба.
8.
Наклонные асимптоты.
9.
Точки пересечения с осями координат.
10.
Нахождение значений функций в некоторых характерных точках.
11.
Построение графика функции.
Пример 1.
Найти наибольшее и наименьшее значение функции
xx
x
y 3
3
2
3
−+= на отрезке [-4;2].
Находим критические точки функции из уравнения 0
=
′
y . Имеем
0
3
2
2
=
−
+
x
x
. Отсюда находим 3,1
2
1
−
=
=
xx . Обе точки принадлежат
отрезку [-4;2].
Далее
3
5
31
3
1
)1(
2
3
−=−+=y ;
9999)3(3)3(
3
)3(
)3(
2
3
=++−=−−−+
−
=−y ;
−−+
−
=−
2
3
)4(
3
)4(
)4(y
3
2
61216
3
64
)4(3 =++−=− ;
3
2
64
3
8
232
3
2
)2(
2
3
=−+=⋅−+=y .
Сравнив эти значения, заключаем, что 9
max
=
y и достигается оно в
точке
3
−
=
x
;
3
5
min
−=y и достигается оно в точке
1
=
x
.
Пример 2.
Исследовать и построить график функции
3
14
2
−
+
=
x
x
y .
1. Областью определения функции является множество
),3()3,(
+∞
−∞
∈
U
x .
2. Функция непрерывна в области определения.
3
=
x
- точка разрыва функции. Прямая
3
=
x
- вертикальная асимптота.
