Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

71
а)
2 2 2
2 4 2
x y z
+ + =
; б)
2 2 2
2 9 36
x y z
− − =
; в)
2 2 2
2 3 4 0
x y z
− + + =
;
г)
2 2
2 2
y z x
+ =
; д)
2 2
z y x
− =
; е)
2
6 0
y z
− =
.
7.
Построить тело, ограниченное указанными поверхностями.
а)
5
y x
=
,
0
y
=
,
3
x
=
,
0
z
=
.
б)
3
y x
=
,
0
z
=
,
0
y
=
,
x z
=
,
2 2
z x y
= +
в)
2 2
4
x y x
+ =
,
0
z
=
,
z x
=
;
г)
2 2
4
x y y
+ =
,
0
z
=
,
6
y z
+ =
;
д)
2 2 2
9
x y z
+ + =
,
2 2
1
x y
+ ≤
,
0
x
≥
;
е)
2 2 2
4( )
x y z
+ =
,
2 2
4
x y
+ =
,
0
y
≥
,
0
z
≥
.
ж)
2 2
4
z x y
= +
,
2 2
5
z x y
= − −
8.
Установить, что плоскость
2 0
x
− =
пересекает эллипсоид
2 2 2
1
16 12 4
x y z
+ + =
по эллипсу; найти его полуоси и вершины.
9.
Установить, что плоскость
1 0
z
+ =
пересекает однополостный гипер-
болоид
2 2 2
1
32 18 2
x y z
− + =
по гиперболе; найти ее полуоси и вершины.
10. Установить, что плоскость
6 0
y
+ =
пересекает гиперболический па-
раболоид
2 2
6
5 4
x y
z
− =
по параболе; найти ее параметр и вершину.

72
4. МАТЕМАТИЧЕСКИЙ АНАЛИЗ. ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ.
4.1. Пределы.
Некоторые утверждения, облегчающие вычисление пределов. Далее будем
предполагать, что величины
)
(
x
α
и
)
(
x
β
являются бесконечно малыми при
a
x
→
, (т.е.
0
=
)
(
lim
x
ax
α
→
,
0
=
)
(
lim
x
ax
β
→
),
)
(
x
Φ
,
)
(
x
Ψ
--- бесконечно большие
при
a
x
→
, (т.е.
∞
Φ
→
=
)
(
lim
x
ax
,
∞
Ψ
→
=
)
(
lim
x
ax
), величина
)
(
x
R
является
ограниченной в некоторой окрестности точки
a
x
=
,
A
x
f
ax
=
)
(
lim
→
,
B
x
g
ax
=
)
(
lim
→
.
Тогда справедливы следующие утверждения:
1.
B
A
x
g
x
f
ax
±
±
→
=
))
(
)
(
(
lim
;
2.
A
x
x
f
ax
=
))
(
)
(
(
lim
α
±
→
;
3.
0
=
))
(
)
(
(
lim
x
x
ax
β
α
±
→
;
4.
∞
±
Φ
→
=
))
(
)
(
(
lim
x
R
x
ax
;
5.
∞
Ψ
−
Φ
→
=
))
(
)
(
(
lim
x
x
ax
, если 1
)(
)(
lim
≠
Ψ
Φ
→ x
x
ax
;
6.
∞
Ψ
+
Φ
→
=
))
(
)
(
(
lim
x
x
ax
, если
0
>
)
(
)
(
x
x
Ψ
⋅
Φ
;
7.
B
A
x
g
x
f
ax
⋅
⋅
→
=
))
(
)
(
(
lim
;
8.
0
=
))
(
)
(
(
lim
x
x
ax
β
α
⋅
→
;
9.
0
=
))
(
)
(
(
lim
x
R
x
ax
⋅
→
α
;
10.
∞
Φ
⋅
→
=
))
(
)
(
(
lim
x
x
f
ax
, если
0
≠
A
;
11.
∞
Ψ
⋅
Φ
→
=
))
(
)
(
(
lim
x
x
ax
;
12.
B
A
xg
xf
ax
=
)(
)(
lim
→
, если
0
≠
B
;
13.
∞
Φ
→
=
)(
)(
lim
xR
x
ax
;
14.
∞
→
=
)(
)(
lim
x
xf
ax
α
, если
0
≠
A
;
15.
0=
)(
)(
lim
x
xR
ax Φ→
.
(Эти утверждения справедливы и в случае, когда
∞
=
a
.)
73
При вычислении пределов часто встречаются пределы выражений
α
α
sin
,
(
)
α
α
/1
1+ при
0
→
α
, которые называются замечательными пределами:
1
0
0sin
lim
0
=
=
→
α
α
α
- первый замечательный предел;
(
)
[
]
e==+
∞
→
11lim
/1
0
α
α
α
- второй замечательный предел.
Примеры
вычисления пределов числовых последовательностей и пределов
функций.
1)
3
1
/13
/7/21
lim
/13
/7/21
lim
13
72
lim
2
2
2
2
2
2
2
2
=
+
−−
=
+
−−
⋅=
∞
∞
=
+
−−
∞→∞→∞→
n
nn
n
nn
n
n
n
nn
nnn
.
2)
7
52
/67
/3/45/32
lim
67
34532
lim
22
−
=
−
−+−−
⋅=
∞
∞
=
−
−+−−
∞→∞→
n
nnn
n
n
n
nnn
nn
.
3)
(
)
[
]
=∞−∞=+−−−
∞→
43232lim
22
nnn
n
=
(
)
(
)
=
+−++
+−+++−−+
∞→
4
3
2
3
2
4323243232
lim
22
2222
n
n
n
nnnnnn
n
(
)
(
)
=
+−++
+−−+
=
∞→
43232
43232
lim
22
22
nnn
nnn
n
=
22
3
/
4
/
3
2
/
3
2
/13
lim
4
3
2
3
2
13
lim
2222
=
+−++
−
⋅=
+−++
−
∞→∞→
n
n
n
n
n
n
n
n
n
n
nn
.
4)
5
3
5
3
12
1
lim
)12)(2(
)1)(2(
lim
0
0
232
2
lim
22
2
2
2
=
−
−
=
−
−
=
−+
−+
=
=
−+
−+
−→−→−→
x
x
xx
xx
xx
xx
xxx
.
5)
(
)
(
)
=
−+
−+
=
−+
++−+
=
=
−+
−+
→→→
)1)(2(
2)1(
lim
)1)(2(
2121
lim
0
0
2
21
lim
11
2
1
xx
x
xx
xx
xx
x
xxx
=
3
1
2
1
lim
)1)(2(
)1(
lim
11
=
+
=
−+
−
→→
xxx
x
xx
.
6)
2
492/7
2/7
)2/7sin(
2lim
)2/7(sin2
lim
0
07cos1
lim
22
0
2
2
0
2
0
=
⋅
⋅==
=
−
→→→
x
x
x
x
x
x
x
x
xxx
.
( При вычислении этого предела использовали первый замечательный
предел
1
sin
lim
0
=
→
α
α
α
).
7) Используем второй замечательный предел
(
)
e=+
→
α
α
α
/1
0
1lim :
[ ]
=
+
−
+==
+
−
−•
+
−
•
−
+
∞→
∞
−
∞→
)13(
12
4
4
12
13
12
4
1lim1
12
32
lim
x
x
x
x
x
x
xx
x

74
6
/12
)/13(4
lim
12
)13(4
lim
−
+
−−
+
−−
=
=
=
∞→∞→
e
e
e
x
x
x
x
xx
.
При раскрытии неопределенностей типа
0
0
и
∞
∞
можно пользоваться
правилом Лопиталя:
Теорема. Пусть функции
)
(
x
f
и
)
(
x
g
дифференцируемы на интервале
)
,
(
b
a
, причем производная
)(xg
′
не обращается в нуль на этом интервале. Если
эти функции являются бесконечно малыми (бесконечно большими величинами)
при
a
x
→
и существует
)(
)(
lim
xg
xf
ax
′
′
→
,
то тогда существует
)(
)(
lim
xg
xf
ax→
и
)(
)(
lim
xg
xf
ax→
=
)(
)(
lim
xg
xf
ax
′
′
→
.
Это правило применимо и в случае, когда
∞
=
a
.
Для раскрытия неопределенности типа
∞
⋅
0
преобразуем соответствующее
произведение
)()(
xgxf
⋅
(предполагаем, что
0)(lim =
→
xf
ax
,
∞=
→
)(lim xg
ax
), в дробь
)(/1
)(
xg
xf
(получим неопределенность типа
0
0
), либо в дробь
)(/1
)(
xf
xg
(получим
неопределенность типа
∞
∞
). В случае неопределенности типа
∞
−
∞
можно
преобразовать разность
)()( xgxf
−
в произведение
[
]
)(/)(1)( xfxgxf
−
⋅
с
последующим применением вышеизложенного.
Неопределенности типов
00
,0,1
∞
∞
раскрывают с помощью
предварительного логарифмирования, после чего возникает неопределенность
типа
∞
⋅
0
.
8)
(
)
( )
3
2
3cos3
2
lim
3sin
1
lim
0
0
3sin
1
lim
2
0
2
0
2
0
−
=
−
=
′
′
−
=
=
−
−
→
−
→
−
→
x
e
x
e
x
e
x
x
x
x
x
x
.
9)
0
2
1
lim
)(
)(
limlim
222
==
′
′
=
∞
∞
=
+∞→+∞→+∞→
x
x
x
x
x
x
ee
x
e
x
.
10)
=
′
′
=
==∞⋅=⋅
−
+→
−
+→
−
+→
)2(
)(
lim
0
0
2
lim]0[}2{lim
/1
00
/1
00
/1
00
xtg
e
xtg
e
xctge
x
x
x
x
x
x
=
==⋅=⋅==
−
+→
−
+→
−
−−
+→
x
te
xx
ex
x
xe
x
x
x
x
x
x
11
lim
3
1
3
)3(cos
lim
)3(cos3
lim
/1
2
00
2
/12
00
2
2/1
00
0
2
lim
3
12
lim
3
1
)(
)(
lim
3
1
lim
3
1
lim
3
1
22
2
==
∞
∞
==
′
′
=
∞
∞
==⋅=
+∞→+∞→+∞→+∞→
−
+∞→
t
t
t
t
t
t
t
t
t
t
ee
t
e
t
e
t
et
.
11)
[
]
∞
→
= 1)(coslim
)(
0
2
xctg
x
x .
75
Пусть Ax
xctg
x
=
→
)(
0
2
)(coslim . Логарифмируя это выражение, получим:
[ ]
=
==⋅∞===
→→→
0
0
)(
cosln
lim0)ln(cos)(lim})ln{(coslimln
2
0
2
0
)(
0
2
xtg
x
xxctgxA
xx
xctg
x
2
1sin
cos2
cos
lim
2)(cos
)sin(cos
lim
)(
)cos(ln
lim
22
0
22
1
0
2
0
−=⋅
−
=
⋅
−⋅
=
′
′
=
→
−
−
→→
x
x
x
x
xx
xx
xtg
x
xxx
.
Далее получаем:
e
eeAA
1
/1
2
1
ln
2/12/1
===⇒−=
−
, следовательно
e
x
xctg
x
1
)(coslim
)(
0
2
=
→
.
Задачи для самостоятельного решения.
Найти пределы числовых последовательностей:
1.
3
n
2n
lim
−
∞→n
2.
5
4n
4-3n
lim
n
+
∞→
3.
3
2n
7n
lim
n
+
+
∞→
4.
4
3n
1n
lim
2
2
n
+
−
∞→
5.
2
5n
3n-n
lim
2
2
n
−
∞→
6.
5
3n
1)(n
lim
3
3
n
−
+
∞→
7.
5
21n
1n
lim
2
3
n
+
−
∞→
8.
1
n
5n
34n
lim
4
3
n
−
+
−
∞→
9.
52
53
n
8n
7n
3n2n
lim
+
−
∞→
10.
4
-
3n
2n
38n11n
lim
2
3
n
+
−+
∞→
11.
5
-
3n
2n
1nn
lim
2
37
n
+
++
∞→
12.
3
4n
8n
49n4n
lim
69
8
n
−
+
−+
∞→
13.
)4n1)(3n(4
n)3)(7n(2n
lim
43
32
n
−+
−+
∞→
14.
4
3
3 2
n
73n
2n5n
lim
n
−
+
∞→
15.
6
5n
4n
3)1n)(2n-(n
lim
2
2
n
+
+
−+
∞→
16.
n84
2n-13n
lim
3 3
2
n
++
+
∞→
n
17.
1
5n
7n
3)(2n5)(3n
lim
4
4
n
−
+
−−+
∞→
18.
4
42
33
7n1)(2n
4n)(32)(n
lin
n
n
++
+−+
∞→
19.
3
34
44
3n-n2)(3n
2n)(31)-(2n
lim
+
−−
∞→
n
20.
1311n
2)1)(nn(n
lim
32
n
+⋅+⋅+
+
+
∞→
nn
21.
53n3)(2
n2
lim
2n
n
+⋅+
⋅
∞→
n
76
22.
nn
nn
n
4
3
2
43
lim
⋅
−
+
∞→
23.
nn
n12n
n
3
5
-
4
3
32
lim
⋅
⋅
−
+
∞→
24.
2n1n
1nn
n
5
2
53
lim
++
+
∞→
+
−
25.
121 - 2)!(n
1)!(n
lim
+
+
∞→
n
26.
! 1)(n n!
! 3)(n2
lim
n
++
+
+
∞→
27.
)1n(n lim
2
n
−−
∞→
28.
n)- nn( lim
2
n
+
∞→
29.
)3n -13n( lim
22
n
n++
∞→
30.
2n)-5n4n( lim
2
+
∞→n
31.
)12n-3n(lim
23 2
n
+
∞→
32.
)1n-n( lim
3
2
3
2
n
+
∞→
33.
2n)-8n1n( lim
3 3
n
+
∞→
34.
)3(n lim
3 3
n
n−+
∞→
35.
2n
1nn1n
lim
2
23
n
+
+−−
∞→
36.
7n
2nnn3n
lim
35
n
+
+−+
∞→
37.
n
3)-1)(n-n(n1)(n
lim
3
n
−+
∞→
38.
)n-(n lim
3 23 2
3
n
nn +⋅
∞→
39.
)7-n-6n(5n lim
n
+⋅+
∞→
40.
(
)
44
4
3
23 lim −−+⋅
∞→
nnn
n
41.
n
n
+
∞→
1-n
1n
lim
42.
n
+
∞→
23n
1-2n
lim
n
43.
;
43
23
lim
n
n
n
n
−
+
∞→
44.
n
+
+
∞
→
72n
54n
lim
n
45.
43
n
32n
12n
lim
−
∞→
+
+
n
46.
14
n
1n
3n
lim
−
∞→
+
−
n
47.
n
n
−
+
∞→
1n
1n
lim
2
2
48.
n
+−
+
∞→
7n2n
n2n
lim
2
2
n
49.
2
53n
13n
lim
2
2
n
n
+
−
∞→
50.
53
2
2
n
1nn
1nn
lim
−
∞→
+−
−+
n
Найти пределы функций:
51.
1
6
9
433
lim
2
2
−
−
++
∞→
х
х
-
хх
x
52.
х
х
-
хх
x
9
5
186
lim
2
2
−
++
∞→
;
53.
1
7
3
24
lim
2
2
+
−
++
∞→
х
х
-
х-х
x
;
54.
4
5
3
68
lim
2
2
+
+
++
∞→
х
х
-
х-х
x
;
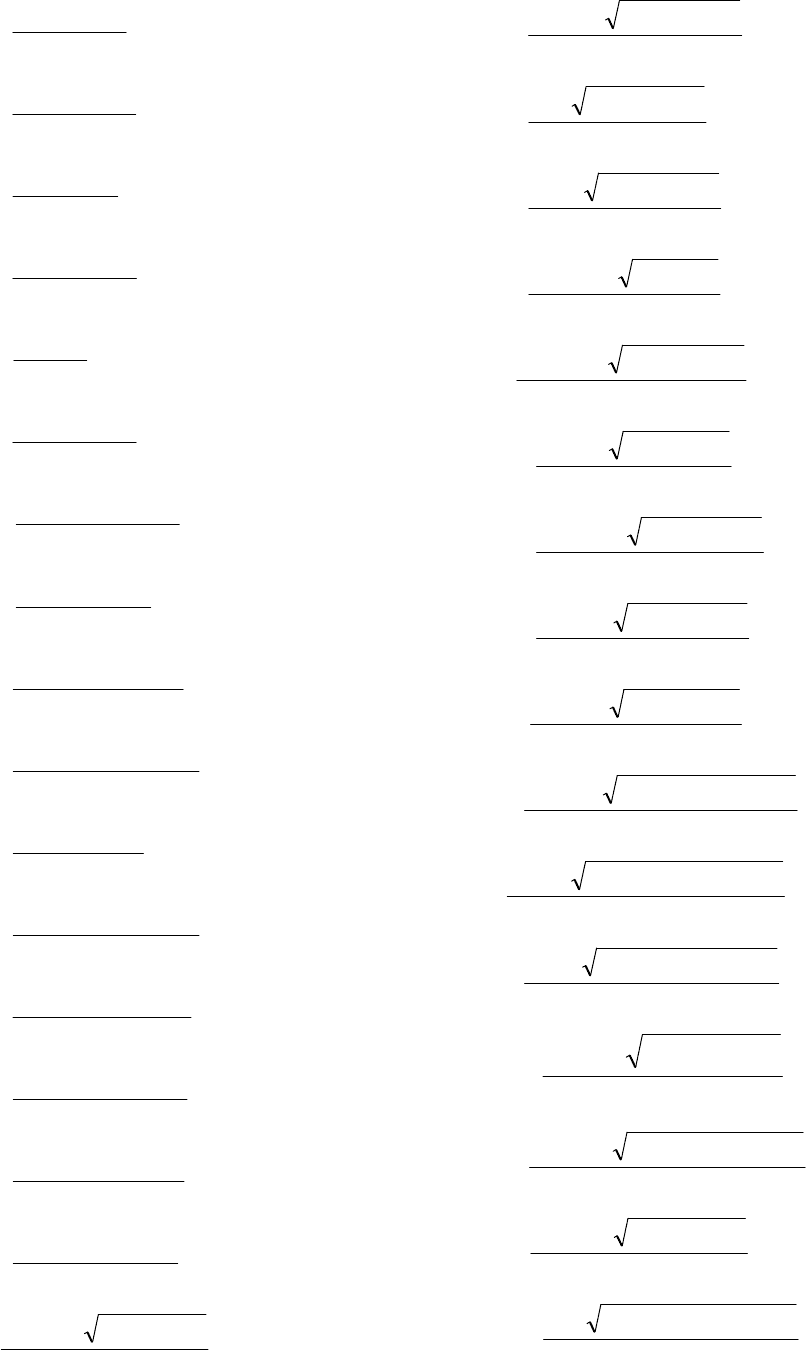
77
55.
х
х
хх
x
8
7
179
lim
2
2
+
+−
∞→
;
56.
8
8
8
853
lim
2
2
−
−
+−
∞→
х
х
-
хх-
x
;
57.
5
2
35
lim
2
2
+
+−
∞→
х
хх
x
;
58.
х
х
-
хх-
x
3
3
387
lim
2
2
+
−−
∞→
;
59.
4
6
98
lim
2
2
+
∞→
х
-х-
x
;
60.
3
5
5
83
lim
2
2
−
+
++
∞→
х
х
-
хх-
x
;
61.
8
3
9
943
lim
23
23
−
−
−
+−+
∞→
х
х
-
х
ххх
x
;
62.
;
6
8
4
276
lim
23
23
−
−
−+
∞→
х
х
-
хх-
x
63.
3
8
7
4483
lim
23
23
−
+
+
++
∞→
х
х
х
хх-х-
x
;
64.
;
4
8
3
6
4588
lim
23
23
+
+
+
+−−
∞→
х
х
х
-
ххх-
x
65.
3
6
6
982
lim
2
23
+
+
−−
∞→
х
х
-
хх
x
;
66.
9
9
4
8
533
lim
23
23
−
+
+
+++
∞→
х
х
х
-
ххх-
x
;
67.
8
2
3
7382
lim
2
23
+
+
+
+++
∞→
х
х
ххх
x
;
68.
;
1
5
7
9
444
lim
23
23
−
−
+
−+
∞→
х
х
х
ххх-
x
69.
;
1
2
9
973
lim
23
23
−
−
+
+++
∞→
х
х
х
-
ххх
x
70.
;
8
5
8
773
lim
23
23
+
+
+
+
∞→
х
х
х
-хх-
x
71.
2
4396
lim
2
+
+−−−
∞→
-
х
xхх
x
;
72.
7
8
66939
lim
2
+
+++
∞→
х
-
хх-х-
x
;
73.
;
5
9
4382
lim
2
−
−−
∞→
х
-
хх-х-
x
74.
;
1
3
27524
lim
2
−
−+
∞→
х
хх-х-
x
75.
8
5
3483
lim
2
+
+−+
∞→
х
-
ххх-
x
;
76.
;
3
7
22423
lim
2
+
−+++
∞→
х
-
ххх-
x
77.
;
7
3
352
lim
2
−
−−++
+∞→
х
ххх
x
78.
9
65799
lim
2
+
−+−−
+∞→
-
х
ххх-
x
;
79.
4
3
93459
lim
2
+
−++
−∞→
х
-
хх-х-
x
;
80.
;
5
4
14319
lim
2
+
+−+−
+∞→
х
ххх
x
81.
4
754576
lim
3 23
−
++−+
+∞→
-
х
xxx-х-
x
;
82.
;
2
5
97466
lim
3 23
−
+−+−+
−∞→
х
xxx--х
x
83.
3
4
22227
lim
3 23
−
+−+−
−∞→
х
xxx-х
x
;
84.
;
2
4
82832
lim
3 3
+
−−−
−∞→
х
-
xx-х
x
85.
2
9
758534
lim
3 23
+
−+−++
+∞→
х
xxxх
x
;
86.
8
7
59532
lim
3 3
−
−−++
+∞→
х
-
xxх
x
;
87.
9
7
35742
lim
3 23
−
+−−−
−∞→
х
-
xxx-х-
x
;
78
88.
;
8
7
635794
lim
3 23
−
−+−++
−∞→
х
xxxх
x
89.
;
1
6
64426
lim
3 3
+
+−+
+∞→
х
xxх--
x
90.
;
2
6
32545
lim
3 23
+
−+−++
+∞→
х
-
xxх-
x
91.
;
)4278()6(
69)1362(
lim
2
++−
++−+−
+∞→
хх- х
х ххх
x
92.
)9212()3(
74)17995(
lim
2
++−
++++−
+∞→
хх- -х
х ххх
x
;
93.
)1589()56(
78)5635(
lim
2
х-х х
х ххх-
x
++−
+++−−
+∞→
94.
;
)2533()73(
66)33366(
lim
2
+++
++−+−
+∞→
хх- х-
х ххх
x
95.
)2359()2(
64)79765(
lim
2
++++
−+++
+∞→
хх х
х х-хх
x
96.
)5468()94(
32)74324(
lim
2
−++
+++++
+∞→
хх- х-
х ххх-
x
;
97.
)5877( )4(7
69)1262(5
lim
2
−+++
+−−+−
+∞→
ххх
х ххх
x
98.
)6262( )74(
4)66893(
lim
2
++−
+++
+∞→
хх-х
х- хх-х-
x
;
99.
)1214()29(
42)15277(
lim
2
+++−
++−−
+∞→
хх х-
х х-хх-
x
100.
;
)9788( )56(
88)4565(
lim
2
х-х-х-
х хх
x
++
+−−−
+∞→
101.
)334977(lim
2
+−
∞→
xx-x-
x
102.
)23636(lim
2
+
∞→
x-x-
x
;
103.
);175(lim
2
++
∞→
xx-x-
x
104.
);491634( lim
2
x-x-x
x
++
∞→
105.
);483676(lim
2
+−−
∞→
xxx-
x
106.
);262555(lim
2
++−+
∞→
xxx
x
107.
);753616(lim
2
++−
∞→
xxx-
x
108.
);264957(lim
2
x-xx
x
+−+
∞→
109.
);69933(lim
2
++−−
∞→
xxx
x
110.
);856478(lim
2
++−+
∞→
xxx
x
111.
);475545( lim
22
x
−+−−+
∞→
xxxx
112.
);599189(lim
22
+−−+−
∞→
xxxx
x
113.
);49555(lim
2
++−−
∞→
xxxx
x
114.
);874134(lim
22
++−−+
∞→
xxxx
x
115.
);5585(lim
22
+−+
∞→
xxx
x
116.
);636246(lim
22
−+−−−
∞→
xxxx
x
117.
);7749(lim
22
−+−++
∞→
xxxx
x
118.
);878678(lim
22
−+−−+
∞→
xxxx
x
119.
);9944(lim
22
+−−+
∞→
xxxx
x
120.
);96756(lim
22
xxxx
x
+−−+
∞→
121.
);5255845x(lim
3 233 23
x
++−−++
∞→
xxxx
122.
);759685x(lim
3 33 23
x
xxxx
+−++−
∞→
79
123.
);5729582x(lim
3 233 23
x
+++−−−+
∞→
xxxxx
124.
);89535353x(lim
3 233 23
x
+++−+−−
∞→
xxxxx
125.
);97648494x(lim
3 233 23
−−−−−−+
∞→
xxxxx
x
126.
);35645x(lim
3 233 3
x
+−−++
∞→
xxx
127.
);17659775x(lim
3 233 23
x
+++−+++
∞→
xxxxx
128.
);623465x3x-4x(lim
3 233 23
x
++−−++
∞→
xxx
129.
);83483-4x-8x(lim
3 233 23
x
−−−−
∞→
xxx
130.
);65928x-9x9x(lim
3 233 23
x
−−+−++
∞→
xxx
131.
99
4362142
lim
2323
−
−−+−+++
∞→
x
xxxxxx
x
;
132.
89
5933433
lim
2323
−
−++−−−+
∞→
x
xxxxxx
x
;
133.
:
95
944834
lim
2323
−
−+−−−+
∞→
x
xxxxxx
x
134.
26
2888698
lim
233
+
+−+−−+
∞→
x
xxxxx
x
;
135.
;
74
3764226
lim
2323
−
−−−+−−
∞→
x
xxxxxx
x
136.
;
15
552263
lim
2323
+
++−−−+−
∞→
x
xxxxxx
x
137.
92
5934854
lim
2323
+
−+−−+−
∞→
x
xxxxxx
x
138.
;
99
4593449
lim
2323
−
−+−−−+
∞→
x
xxxxx
x
139.
;
34
552792
lim
33
−
+−+−
∞→
x
x-xxx
x
140.
;
3
16782558
lim
2323
+
−−−−−
∞→
x
xx-xx-xx
x

80
141.
4
3
283
lim
2
2
4
−
+
++−
−→
x
x
xx
x
142.
;
44
3
2
4885
lim
2
2
4
−
−
+−−
−→
x
x
xx
x
143.
;
36
21
3
283
lim
2
2
4
−
+
+−−
→
x
x
-
xx
x
144.
8
18
5
43
lim
2
2
4
+
+
−
++−
→
x
x
xx
x
145.
24
30
9
8184
lim
2
2
4
−
−
+−
→
x
x
xx
x
;
146.
;
7
2
9
4117
lim
2
2
1
−
−+−
→
x
-
x
xx
x
147.
2
5
3
422
lim
2
2
2
+
−
−
+−−
−→
x
x
xx
x
148.
;
12
20
8
15174
lim
2
2
3
−
+
++
−→
x
x
xx
x
149.
;
3
26
9
2110
lim
2
2
3
−
−
+−
→
x
x
xx
x
150.
;
12
14
6
27307
lim
2
2
3
−
+
−−−
−→
x
x
xx
x
151.
;
6
29
21
4
6135
lim
23
2
3
+
−
+
++−
→
x
x
x
-
xx
x
152.
;
21
28
13
2
2185
lim
23
2
3
−
+
−
++−
→
x
x
x
xx
x
153.
;
2
6
7
972
lim
23
2
1
−
−
+
+−−
→
x
x
x
xx
x
154.
;
8
22
4
6117
lim
23
2
2
+
+
+
+−−
−→
x
x
x
-
xx
x
155.
;
3
7
25
9
1574
lim
23
2
3
+
−
−
++−
→
x
x
x
xx
x
156.
;
1
5
12
8
2
lim
23
2
1
+
+
+
++−
−→
x
x
x
xx
x
157.
;
18
3
9
2
372
lim
23
2
3
+
+
−
+−
→
x
x
x
xx
x
158.
;
24
14
26
8
352
lim
23
2
3
+
+
+
−+
−→
x
x
x
xx
x
159.
;
3
11
8
682
lim
23
2
1
x
x
x
xx
x
+
−
−+−
→
160.
;
1
2
8
7
45
lim
23
2
1
−
+
−
+−
→
x
x
x
xx
x
161.
;
8
14
13
2
105189
lim
23
23
2
+
−
−
++−−
−→
x
x
x
-
xxx
x
162.
;
8
16
20
7
633
lim
23
23
2
+
+
+
−+
−→
x
x
x
xxx
x
163.
;
18
24
33
9
21232
lim
23
3
1
−
−
+
−+−
→
x
x
x
xx
x
164.
;
12
5
24
7
27962
lim
23
23
3
+
+
−
+−+−
→
x
x
x
xxx
x
165.
;
6
11
3
5
10584
lim
23
23
2
x-
x
x
-
xxx
x
+
−
−−+
−→
166.
;
8
2
5
11072
lim
23
23
1
−
−
+
+++−
−→
x
x
-x
xxx
x
167.
;
9
24
5
4
91232
lim
23
23
3
−
−
+
++−−
−→
x
x
x
xxx
x
168.
;
3
2
2
2110103
lim
23
23
3
−
−
−
−+−
→
x
x
x
xxx
x
169.
;
6
7
6
2
166
lim
23
23
2
−
+
−
+−−
→
x
x
x
xxx
x
170.
;
8
4
6
2
51229
lim
23
23
1
+
−
−
+−−
→
x
x
x
xxx
x
171.
;
3
3128
lim
2
3
−
−−+
→
x
xx
x
172.
;
2
152
lim
2
2
−
−−−
→
x
xx
x
173.
;
2
104
lim
2
2
+
−+−
−→
x
xx
x
174.
;
2
5175
lim
2
2
−
−−−
→
x
xx
x
