Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

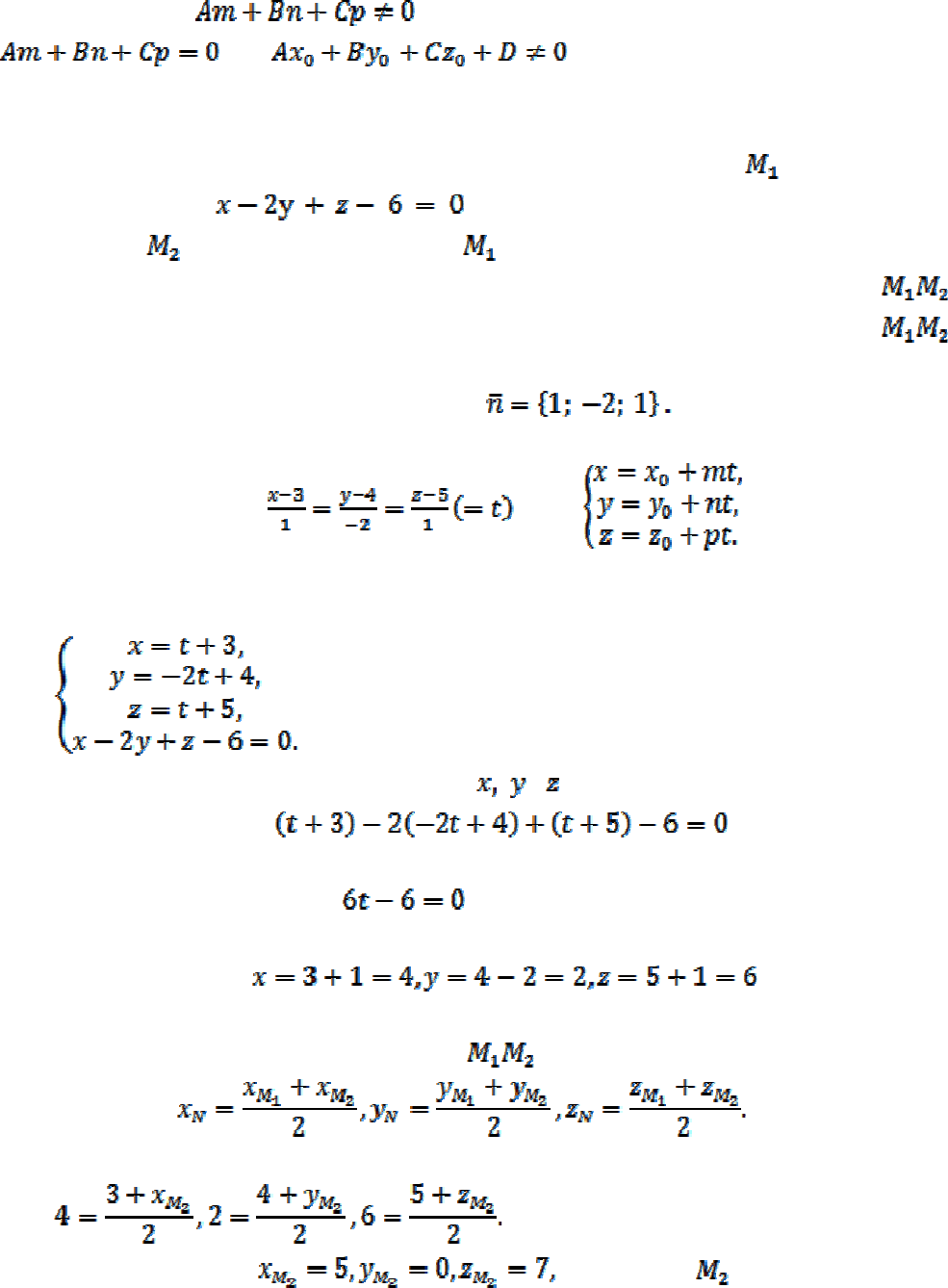
51
(Если , то прямая пересекает плоскость; если
и — прямая параллельна плоско-
сти.)
Пример 7
. Найти координаты точки, симметричной точке (3;4;5) относи-
тельно плоскости
.
Точка
, симметричная точке относительно плоскости, принадлежит
прямой, перпендикулярной к плоскости и является концом отрезка
,
который пересекает плоскость в точке N . Причем N - середина отрезка
.
Направляющий вектор прямой, перпендикулярной к плоскости совпадает с
нормальным вектором данной плоскости
Составим уравнение прямой, перпендикулярной к плоскости
или
Координаты точки N пересечения этой прямой с плоскостью находим, решая
систему
Подставляем значения переменных
, в уравнение плоскости, получим
,
откуда
т.е. t = 1.
Следовательно,
,
т.е. N(4;2;6) — точка пересечения прямой и плоскости.
А так как точка N — середина отрезка
, то
Имеем
Отсюда находим
т.е. точка имеет координаты
(5;0;7).
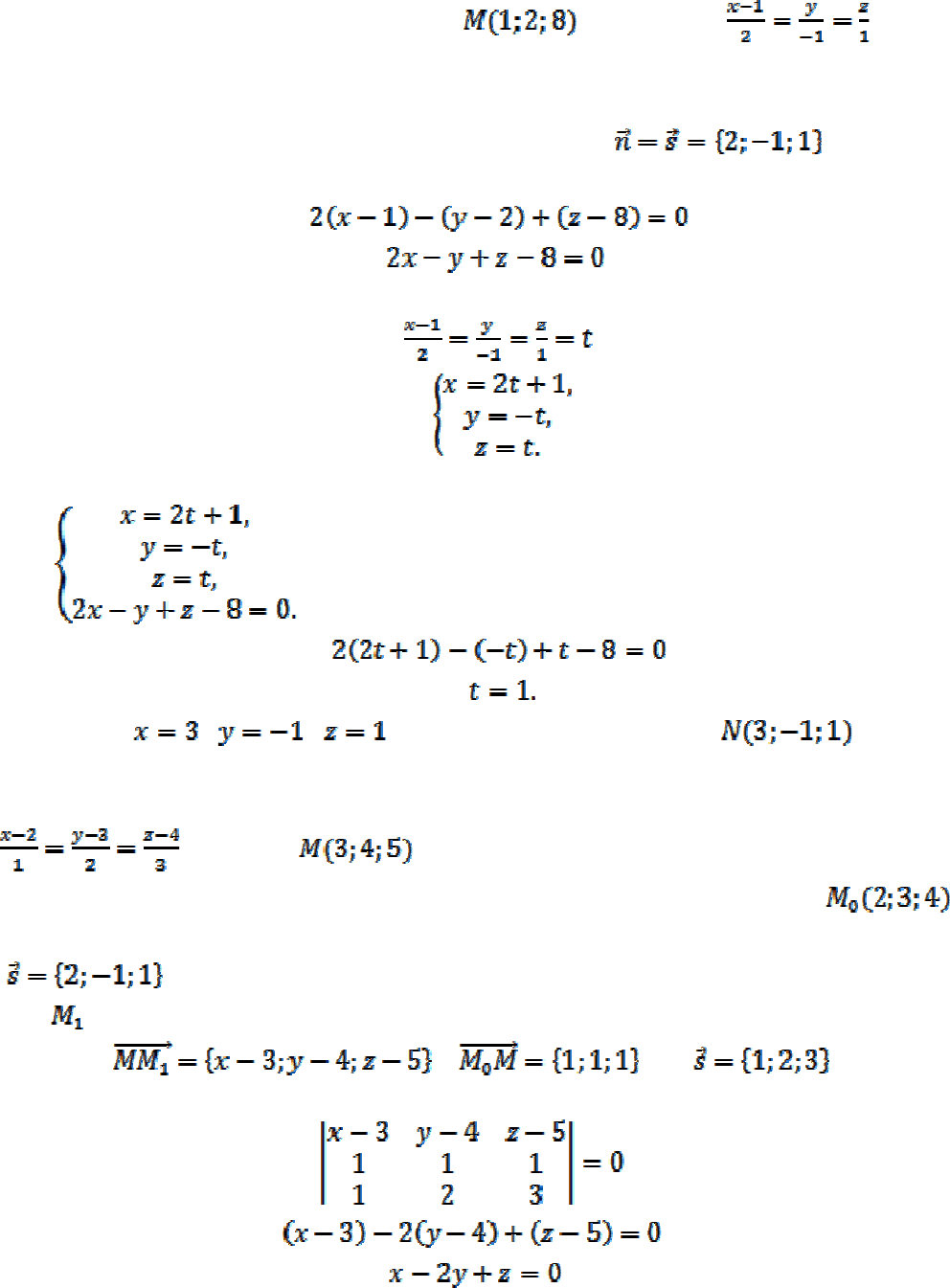
52
Пример 8
. Найти проекцию точки на прямую .
Обозначим искомую точку через N. Точка N - точка пересечения данной
прямой и плоскости к ней перпендикулярной. Нормальный вектор плоскости
совпадает с направляющим вектором прямой, т.е.
. Составим
уравнение плоскости
,
.
Уравнения данной прямой запишем в параметрической форме
,
Для определения координат точки N составим систему и решим ее:
,
Тогда
, , . Таким образом получим - .
Пример 9
. Написать уравнение плоскости, проходящей через прямую
и точку .
По условию прямая лежит в плоскости, это значит, что точка
также принадлежит этой плоскости, а направляющий вектор прямой
параллелен искомой плоскости. Выберем текущую точку плоско-
сти
(x;y;z). Рассмотрим векторы
, и .
Эти векторы компланарны, условие их компланарности запишется в виде
,
,
-
искомое уравнение плоскости.
53
Задачи для самостоятельного решения.
1.
Даны точки
(3; 2; 1)
A
− −
,
(0;0; 2)
B
−
,
( 3;1;0)
C
−
,
( 4; 2;2,5)
D
− −
. Укажите,
какие из них принадлежат плоскости
2 3 4 0
x y z
− + =
. (Ответ: точки
А,В и D.)
2.
Составить уравнение плоскости, проходящей через точку
0
( 3;0;2)
M
−
и
перпендикулярно вектору
)5;3;2(
=
n
r
. (Ответ:
2 3 5 4 0
x y z
+ + − =
.)
3.
Составить уравнение плоскости, проходящей через точку
0
(3;4;5)
M
и
перпендикулярно вектору
)2;3;1(
−
−
=
n
r
. (Ответ:
3 2 5 0
x y z
+ − − =
.)
4.
Составьте уравнение плоскости, проходящей через точку
0
(2; 3; 1)
M
− −
и перпендикулярно вектору
21
MM , где
1
(3;4;1)
M
и
2
(1; 2; 3)
M
− −
. (От-
вет:
3 2 9 0
x y z
+ + + =
.)
5.
Даны точки
(3; 2;4)
A
−
и
(1;4;2)
B
. Составьте уравнение плоскости, про-
ходящей через точку А и перпендикулярной вектору
AB
. (Ответ:
3 7 0
x y z
− + − =
.)
6.
Составьте уравнение плоскости, проходящей через точку
(1; 1;2)
M
−
перпендикулярно к отрезку
1 2
M M
, если
1
(2;3; 4)
M
−
,
2
( 1;2; 3)
M
− −
. (От-
вет:
3 0
x y z
+ − =
.)
7.
Составить уравнение плоскости в «отрезках», если она проходит через
точку
(6; 10;1)
M
−
и отсекает на оси Ох отрезок
3
−
=
a
, а на оси Оz – от-
резок
2
=
c
. (Ответ:
1
2
4
3
=+
−
+
−
zyx
.)
8.
Составить уравнение плоскости, которая проходит через точку
(2; 3; 4)
M
− −
и отсекает на осях координат отличные от нуля отрезки
одинаковой величины. (Ответ:
5 0
x y z
+ + + =
.)
9.
Составьте уравнение плоскости, параллельной плоскости хОу и прохо-
дящей через точку
0
(2; 2;3)
M
−
. (Ответ:
3 0
z
− =
.)
10.
Найти величины отрезков, отсекаемых на осях координат плоскостью,
проходящей через точку
(2; 3;3)
M
−
параллельно плоскости
3 3 0
x y z
+ − =
. (Ответ:
( 2; 6;2)
− −
.)
11.
Найти величины отрезков, отсекаемых на осях координат плоскостью,
проходящей через точку
( 2;7;3)
M
−
параллельно плоскости
4 5 1 0
x y z
− + − =
. (Ответ:
1/15;4/15; 1/ 3
− −
.)
12.
Составить уравнение плоскости, проходящей через середину отрезка
1 2
M M
перпендикулярно к этому отрезку, если
1
(1;5;6)
M
,
2
( 1;7;10)
M
−
.
(Ответ:
2 22 0
x y z
− − + =
.)
13.
Составить уравнение плоскости, перпендикулярной оси Ох и проходя-
щей через точку
0
(2; 1;3)
M
−
. (Ответ:
2 0
x
− =
.)
54
14.
Составьте уравнение плоскости, перпендикулярной оси Оz и проходя-
щей через точку
0
( 2; 3; 1)
M
− − −
. (Ответ:
1 0
z
− =
.)
15.
Составьте уравнение плоскости, параллельной плоскости хОz и прохо-
дящей через точку
0
( 3; 2;4)
M
− −
. (Ответ:
2 0
y
+ =
.)
16.
Составьте уравнение плоскости, проходящей через ось Ох и через точ-
ку
(3;2;4)
M
. (Ответ:
2 0
y z
− =
.)
17.
Составьте уравнение плоскости, проходящей через ось Оz и через точ-
ку
(1;1;1)
M
. (Ответ:
0
x y
− =
.)
18.
Составьте уравнение плоскости, проходящей через ось Оу и через точ-
ку
( 2; 3; 4)
M
− − −
. (Ответ:
2 0
x z
− =
.)
19.
Составьте уравнение плоскости, параллельной оси Оz и проходящей
через точки
1
(3; 1;2)
M
−
и
2
( 2;3;4)
M
−
. (Ответ:
4 5 7 0
x y
+ − =
.)
20.
Составьте уравнение плоскости, параллельной оси Оу и проходящей
через точки
1
(1; 2; 1)
M
− −
и
2
(3;2; 4)
M
−
. (Ответ:
3 2 1 0
x z
+ − =
.)
21.
Составьте уравнение плоскости, параллельной оси Ох и проходящей
через точки
1
( 4;2;5)
M
−
и
2
( 5; 1;3)
M
− −
. (Ответ:
2 3 11 0
y z
− + =
.)
22.
Составьте уравнение плоскости, проходящей через точку
0
(2; 1;3)
M
−
и
параллельной векторам
)1;0;3(
−
=
a
r
и
)2;2;3(−=b
r
. (Ответ:
2 3 6 25 0
x y z
− + − =
.)
23.
Составьте уравнение плоскости, проходящей через точки
(2;3; 5)
M
−
и
( 1;1; 6)
N
− −
параллельно вектору
)3;4;4(
=
a
r
и. (Ответ:
2 5 4 31 0
x y z
− + + =
.)
24.
Составьте уравнение плоскости, проходящей через точку
0
( 4; 3;1)
M
− −
и параллельной векторам
)3;2;5(
−
=
a
r
и
)2;4;1( −=b
r
. (От-
вет:
8 7 18 35 0
x y z
+ + + =
.)
25.
Составить уравнение плоскости, проходящей через точку
( 2;3;4)
M
−
и
параллельной плоскости
2 3 4 0
x y z
+ − + =
. (Ответ:
2 3 8 0
x y z
+ − + =
.)
26.
Составить уравнение плоскости, проходящей через точку
( 1; 2;3)
M
− −
и
параллельной плоскости
2 3 1 0
x y z
− + − =
. (Ответ:
2 3 7 0
x y z
− + − =
.)
27.
Составить уравнение плоскости, проходящей через точки
1
( 2; 3;1)
M
− −
и
2
(1;4; 2)
M
−
и перпендикулярной плоскости
2 3 4 0
x y z
+ − + =
. (Ответ:
2 3 5 0
x y z
− − =
.)
28.
Составить уравнение плоскости, проходящей через точки
(1; 4; 3)
A
− −
и
(4; 2; 1)
B
− −
и перпендикулярной плоскости
3 7 0
x y z
− − + =
. (Ответ:
2 9 0
x y z
− + − =
.)
29.
Составить уравнение плоскости, проходящей через точки
1
(2; 1; 3)
M
− −
и
2
( 3;4;1)
M
−
и перпендикулярной плоскости
3 2 0
x y z
− − + =
. (Ответ:
1 0
x y
+ − =
.)

55
30.
Составьте уравнение плоскости, проходящей через точку
( 1; 1;2)
M
− −
и
перпендикулярной плоскостям
2 2 4 0
x y z
+ − + =
и
2 4 0
x y z
− + − =
.
(Ответ:
2 3 4 3 0
x y z
+ + − =
.)
31.
Составить уравнение плоскости, проходящей через начало координат
перпендикулярно к плоскостям
5 7 0
x y z
+ − + =
и
3 2 3 0
x y z
− + − =
.
(Ответ:
9 5 16 0
x y z
− − =
.)
32.
Найти острый угол между плоскостями
2 3 4 1 0
x y z
− + − =
и
3 4 3 0
x y z
− − + =
. (Ответ:
1259
′
=
o
ϕ
.)
33.
Найдите острый угол между плоскостями
1 0
x y z
− + + =
и
2 3 3 0
x y z
+ − − =
. (Ответ:
2072
′
=
o
ϕ
.)
34.
Определить, при каком значении В плоскости
4 1 0
x y z
− + − =
и
2 10 3 0
x By z
+ + − =
будут перпендикулярны. (Ответ:
3
B
=
.)
35.
Определить, при каком значении С плоскости
3 5 3 0
x y Cz
− + − =
и
3 2 5 0
x y z
− + + =
будут перпендикулярны. (Ответ:
9
C
= −
.)
36.
Найти расстояние от точки
(2;3;4)
A
до плоскости
4 3 12 5 0
x y z
+ + − =
.
(Ответ:
60/13
.)
37.
Найдите расстояние от точки
(1; 2;1)
A
−
до плоскости
10 2 11 10 0
x y z
− + − =
. (Ответ: 1.)
38.
Найдите расстояние от точки
(2;3; 2)
A
−
до плоскости
6 7 6 22 0
x y z
− − − =
. (Ответ:
11
.)
39.
Найдите расстояние между параллельными плоскостями
2 3 6 28 0
x y z
− + + =
и
2 3 6 14 0
x y z
− + − =
. (Ответ: 6.)
40.
Найдите расстояние между параллельными плоскостями
2 4 0
x y z
− + − =
и
2 10 0
x y z
− + + =
. (Ответ:
6
.)
41.Составить канонические уравнения прямой , проходящей через точку
(3; 1;2)
A
−
a)
параллельно вектору
(2;1; 3)
а
−
r
;
b)
параллельно оси Оу;
c)
параллельно прямой
5 2 3
4 2 1
x y z
− + −
= =
−
.
42.
Составить параметрические уравнения прямой, проходящей через точ-
ку
(2;4; 5)
B
−
а)
параллельно вектору
(0; 1;3)
m
−
r
;
б)
параллельно оси Оz;
в)
параллельно прямой
1 4
1 2 3
x y z
+ −
= =
−
.
43.
Составить канонические уравнения прямой, проходящей через две точ-
ки
(2; 5;0)
A
−
и
(3; 1;4)
B
−
и записать его в параметрическом виде.
44.
Составить параметрические уравнения прямой, проходящей через точ-
ки
(2;2; 3)
A
−
и
(1; 0; 1)
B
−
и записать их в каноническом виде.

56
45.
Дана прямая
3 2 0
2 2 3 1 0
x y z
x y z
− + − =
+ − + =
.
а)
Найти какой-нибудь ее направляющий вектор
m
r
.
б)
Записать уравнения этой прямой в каноническом виде.
46.
Дана прямая
2 4 5 0
4 2 3 0
x y z
x y z
+ − − =
− + + =
.
а)
Найти какой-нибудь ее на направляющий вектор
m
r
.
б)
Записать уравнения этой прямой в каноническом виде.
47.
Составить канонические и параметрические уравнения следующих
прямых:
а)
4 3 0
2 8 0
x y
x y z
+ − =
− + + =
; б)
2 4 8 0
2 1 0
x y z
x y z
− + − =
+ − − =
;
в)
3 2 0
3 2 0
x y z
x y z
+ + + =
− − − =
; г)
7 2 4 0
3 4 0
x y
x z
− + =
+ =
.
48.
Проверить, параллельны ли прямые
а)
2 2
1
3
x t
y t
z
= −
= − +
=
и
2 4 5 3 0
2 3 7 0
x y z
x y z
+ − + =
+ + − =
.
б)
2 1
6 3 4
x y z
− +
= =
− −
и
2 3 2 0
2 8 3 1 0
x y z
x y z
− + − =
+ − + =
.
49.
Проверить, перпендикулярны ли прямые
а)
3
2 2
4
x t
y t
z t
=
= − +
= − +
и
2 4 0
3 2 0
x y z
x y
− + − =
+ − =
.
б)
3 1 0
2 9 0
x y z
x y z
+ − − =
− − =
и
2 2 5 0
2 2 2 0
x y z
x y z
+ + + =
− − + =
.
50.
Найти точки пересечения прямой, проходящей через точки
1
(2;0; 4)
A
−
и
2
(3;1; 5)
A
−
, с координатными плоскостями.
51.
Найти точки пересечения прямой, проходящей через точки
1
( 1;3; 2)
B
− −
и
2
(2; 1; 4)
B −
, с координатными плоскостями.
52.
Даны вершины треугольника АВС.
(2; 5;4)
A
−
,
(3; 2; 1)
B
−
,
(0; 4; 3)
C
−
. Со-
ставить:
а) уравнение стороны АВ треугольника АВС;
б) уравнение медианы, проведенной из вершины А;

57
в) уравнение средней линии треугольника АВС, параллельной сто-
роне АВ;
г) уравнение биссектрисы его внутреннего угла при вершине С;
д) уравнение его высоты, опущенной из вершины В.
52.
Вычислить угол между прямой
2 1 3
3 4 2
x y z
− + −
= =
и плоскостью
2 3 4 0
x y z
+ − + =
. (Ответ:
14 22
ϕ
′
=
o
.)
53.
Вычислить угол между прямой
4 1 3
3 2 4
x y z
+ − −
= =
и плоскостью
2 3 2 5 0
x y z
− − + =
. (Ответ:
21 07
ϕ
′
=
o
.)
54.
Составить уравнение плоскости, проходящей через точку
( 1; 2; 3)
M
− −
перпендикулярно прямой
2 1 3
4 3 2
x y z
+ − +
= =
. (Ответ:
4 3 2 4 0
x y z
+ + + =
.)
55.
Составить уравнение плоскости, проходящей через точку
(2; 1; 4)
M
− −
перпендикулярно прямой
3 2 5
2 4 3
x y z
− + +
= =
. (Ответ:
2 4 3 12 0
x y z
+ + + =
.)
56.
Через точку
(1;3; 2)
M
провести прямую, перпендикулярную плоскости
2 2 3 0
x y z
− + − =
. (Ответ:
1 3 2
1 2 2
x y z
− − −
= =
−
.)
57.
Составьте уравнение перпендикуляра к плоскости
4 5 3 0
x y z
− − − =
, про-
ходящего через точку
( 1;1; 2)
M
− −
. (Ответ:
1 1 2
4 5 1
x y z
+ − +
= =
− −
.)
58.
Найти точку пересечения прямой
2 3 1
4 2 5
x y z
− − +
= =
с плоскостью
2 3 4 0
x y z
+ − − =
.(Ответ:
(6;5; 4)
.)
59.
Найти точку пересечения прямой
3 1 5
2 3 2
x y z
+ − +
= =
с плоскостью
2 3 22 0
x y z
+ + − =
.(Ответ:
(1;7; 1)
−
.)
60.
Составьте уравнение перпендикуляра к плоскости
3 2 26 0
x y z
− + − =
,
проходящего через точку
( 2; 2; 4)
− −
. Найдите координаты основания
этого перпендикуляра (Ответ:
2 2 4
1 3 2
x y z
+ − +
= =
;
(1; 7;2)
−
.)
61.
Убедиться в том, что прямая
2 4 1
4 3 2
x y z
− + −
= =
−
параллельна плоскости
5 2 7 3 0
x y z
− + + =
.
62.
Проверьте, что прямая
1 4 1
2 3 3
x y z
− − +
= =
− −
параллельна плоскости
3 5 3 4 0
x y z
− − − =
.
63.
Проверьте, что прямая
3 1 2
4 2 3
x y z
− − +
= =
лежит в плоскости
2 2 9 0
x y z
− − − =
.

58
64.
Проверьте, что прямая
1 3 4
2 1 5
x y z
− + −
= =
−
лежит в плоскости
3 4 2 7 0
x y z
− − − =
.
65.
Составить уравнение плоскости, проходящей через прямую
2 3 4 0,
3 0
x y z
x y z
+ − + =
− + + =
и точку
(2;1; 1)
M
−
. (Ответ:
2 5 7 8 0
x y z
− + + =
.)
66.
Составить уравнение плоскости, проходящей через прямую
2 4 5 5 0,
2 2 1 0
x y z
x y z
− + + =
− + − =
и точку
(3; 2;1)
M
. (Ответ:
4 2 7 0
x y z
+ − − =
.)
67.
Составить уравнение плоскости, проходящей через точку
(3; 4;0)
M
и
прямую
2 3 1
1 2 2
x y z
− − +
= =
. (Ответ:
4 0
y z
− − =
.)
68.
Составить уравнение плоскости, проходящей через две параллельные
прямые
3 1
2 1 2
x y z
− −
= =
и
1 1
2 1 2
x y z
+ −
= =
. (Ответ:
2 2 1 0
x y z
+ − − =
.)
69.
Показать, что прямая
3 1
6 8 9
x y z
− −
= =
−
параллельна плоскости
3 2 1 0
x y z
+ − − =
, а прямая
7, 2, 2 1
x t y t z t
= + = − = +
лежит в этой плоскости.
70.
Составить уравнение плоскости, проходящей через точку
(2;3; 1)
M
−
и
прямую
3, 2 5, 3 1
x t y t z t
= − = + = − +
. (Ответ:
10 13 12 47 0
x y z
+ + − =
.)
71.
Найти проекцию точки
(4; 3;1)
M
−
на плоскость
2 15 0
x y z
− − − =
. (Ответ:
1
(5; 5;0)
M −
.)
72.
При каких значениях n и А прямая
5 5
3 6
x y z
n
− +
= =
перпендикулярна к
плоскости
2 2 7 0
Ax y z
+ − − =
? (Ответ: А=-1, n=-6.)
73.
Доказать, что прямая
1 1 3
2 1 3
x y z
+ + −
= =
−
параллельна плоскости
2 0
x y z
+ − =
, а прямая
2 4
2 1 3
x y z
− −
= =
−
лежит в этой плоскости.
74.
Доказать, что прямая
1 2 1
2 3 6
x y z
− + −
= =
−
перпендикулярна к прямой
2 4 2 0,
4 5 4 0
x y z
x y z
+ − + =
− − + =
.
75.
Найти точку пересечения прямой
1 1
1 2 6
x y z
− +
= =
−
и плоскости
2 3 1 0
x y z
+ + − =
.(Ответ:
(2;3;6)
M
.)
76.
Найти проекцию точки
(3;1; 1)
P
−
на плоскость
2 3 30 0
x y z
+ + − =
. (Ответ:
1
(5;5;5)
P
.)
77.
При каком значении А плоскость
3 5 1 0
Ax y z
+ − + =
параллельна прямой
1 2
4 3 1
x y z
− +
= =
? (Ответ: А=-1.)

59
78.
При каких значениях m и С прямая
2 1 5
4 3
x y z
m
− + −
= =
−
перпендикулярна к
плоскости
3 2 1 0
x y Cz
− + + =
? (Ответ: С=1,5 , m=-6.)
79.
При каких значениях А и В плоскость
6 7 0
Ax By z
+ + − =
перпендику-
лярна к прямой
2 5 1
2 4 3
x y z
− + +
= =
−
? (Ответ: А=4, В=-8.)
80.
Показать, что прямая
3 1
6 8 9
x y z
− −
= =
− −
параллельна плоскости
3 1 0
x y z
+ − + =
, а прямая
7, 2, 2 1
x t y t z t
= + = − = +
лежит в этой плоскости.
81.
Найти точку пересечения прямой
7 1 5
5 1 4
x y z
− − −
= =
и плоскости
3 2 8 0
x y z
− + − =
.(Ответ:
(2;0;1)
M
.)
82.
При каких значениях В и D прямая
2 9 0
x y z
− + − =
,
3 0
x By z D
+ + + =
лежит в плоскости Оху? (Ответ: В=-6 , D=-27.)
83.
Найти точку, симметричную точке
(4;3;10)
M
относительно прямой
1 2 3
2 4 5
x y z
− − −
= =
. (Ответ:
1
(2;9;6)
M
.)
3.3. Кривые второго порядка.
Кривые второго порядка - это линии, уравнения которых в прямо-
угольной системе координат являются уравнениями второй степени. Рас-
смотрим четыре вида кривых второго порядка: окружность, эллипс, гипербо-
ла и парабола.
Окружностью называется множество всех точек плоскости равноуда-
ленных от данной точки, называемой центром.
Эллипсом называется множество всех точек плоскости, для которых
сумма расстояний до двух данных точек, называемых фокусами, есть вели-
чина постоянная, большая, чем расстояние между фокусами.
Гиперболой называется множество всех точек плоскости, для которых
модуль разности расстояний до двух данных точек, называемых фокусами,
есть величина постоянная, меньшая, чем расстояние между фокусами.
Параболой называется множество всех точек плоскости, каждая из ко-
торых находится на одинаковом расстояние от данной точки, называемой
фокусом, и от данной прямой, называемой директрисой.
Для каждой из кривых второго порядка можно выбрать такую декарто-
ву систему координат, в которой уравнение кривой будет иметь наиболее
простой вид, этот вид называется каноническим.

60
Кривые
второго
порядка.
Канониче-
скоеуравне-
ние.
Фокальное рас-
стояние(с).
Эксцентри-
ситет
)
(
ε
.
Чертеж.
1.
эллипс
1
2
2
2
2
=+
b
y
a
x
222
b
a
с
−
=
а
с
ε =
;
1
0
<
<
ε
2.
гипербола
1
2
2
2
2
=−
b
y
a
x
222
b
a
с
+
=
а
с
ε =
;
1
>
ε
3.
парабола
pxy 2
2
=
2
р
с =
1
=
ε
Через
1
F и
2
F обозначены фокусы эллипса и гиперболы,
F
фокус па-
раболы, l - директриса параболы. Числа a, b, c, p положительны. Расстояние
между фокусами для эллипса и гиперболы равно 2с. Расстояние между фоку-
сом и директрисой для параболы равно р.
Оси симметрии эллипса называются его осями. Точка пересечения осей
симметрии называется центром эллипса. Точки, в которых эллипс пересекает
оси, называются его вершинами. Вершины ограничивают на осях отрезки
