Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.


21
−++
−−
−
+
+
−
10=683
35=745
24=462
321
321
321
xxx
xxx
xxx
Решение:
Прямой ход метода Гаусса.
−
−−
−
−
10|683
35|745
|
24462
2
5
−
−
2
3
−
−
−−
−
−
92|24340
50|6220
Делим элементы строки 1 на 2
Делим элементы строки 2 на 2
−−
−
−
46|12170
|
253110
11
17
−
(
)
81|8100
−
Обратный ход метода Гаусса.
Из равенства 81=81
3
−
⋅
x следует, что 1=
3
−
x .
Далее находим:
2
11 x
⋅
−
3
3 x
⋅
−
25
=
⇒
2
11
x
⋅
−
1)
(
3
−
⋅
−
25
=
2=
2
−
⇒
x
.
1
2
x
⋅
−
2
6
x
⋅
+
3
4
x
⋅
+
24
=
−
⇒
1
2
x
⋅
−
2)
(
6
−
⋅
+
1)
(
4
−
⋅
+
24
=
−
4=
1
x
⇒
.
Ответ:
4=
1
x
; 2=
2
−
x
; 1=
3
−
x
.
В процессе выполнения прямого хода метода Гаусса может получится
строка имеющая вид
)
|
0
...
0
(0
d
, где число
0
≠
d
. Это означает, что исходная
система уравнений не имеет решения.
Приведем пример системы, которая не имеет решения.
Пример 4.
Найти все решения следующей системы уравнений:
−++−
−+−+−
−++−
−+−+−
51=1221813
50=137104
28=7825
7=2543
4321
4321
4321
4321
xxxx
xxxx
xxxx
xxxx
Решение:
Прямой ход метода Гаусса.

22
−−
−−−
−−
−
−
−
51|1221813
50|137104
28|7825
| 72543
3
5
−
−
3
4
−
3
13
−
−
−−
−−
−
−
244|622280
122|311140
119|311140
Делим элементы строки 3 на 2
−−
−−
−
−
122|311140
122|311140
| 119311140
14
14
−
14
14
−
−
−
42|0000
42|0000
Делим элементы строки 1 на 42
Делим элементы строки 2 на 42
−
−
1|0000
1|0000
Так как в процессе прямого хода метода Гаусса получили строку
)
1
|
0
...
0
(
−
, то система уравнений не имеет решения.
Ответ:
Система не имеет решения.
Если в процессе выполнения обратного хода метода Гаусса после
подстановки найденных ранее неизвестных будет получено уравнение с
несколькими неизвестными, то все неизвестные кроме одного надо объявить
параметрами, выразить оставшееся неизвестное через параметры и продолжить
выполнение обратного хода метода Гаусса. В этом случае система уравнений
имеет бесчисленное множество решений, которые и будут найдены во время
обратного хода.
Далее приведем пример системы уравнений, которая имеет бесчисленное
множество решений.
Пример 5.
Найти все решения следующей системы уравнений:
−−++−
−+−−
−+−+
−+−+
6=8263
43=48925
35=35634
49=43872
4321
4321
4321
4321
xxxx
xxxx
xxxx
xxxx
Решение:

23
Прямой ход метода Гаусса.
−−−
−−−
−−
−
−
6|8263
43|48925
35|35634
| 4943872
2
4
−
2
5
2
3
−−
−−
−
−
159|11320330
159|11922310
126|10220220
Делим элементы строки 1 на 2
−−
−−
−
−
159|11320330
159|11922310
| 635110110
11
31
−
−
11
33
−
−
−−
−
−
330|44011000
204|2726800
Делим элементы строки 1 на 68
Делим элементы строки 2 на 110
−−
−
−
3|4100
| 34100
1
1
−
Так как в процессе прямого хода метода Гаусса получили матрицу вида:
(
)
0|0000
то прямой ход закончен и начинаем обратный ход, причем начинаем его с
последней выделенной (подчеркнутой) строки, в которой есть хотя бы один не
нулевой элемент.
Обратный ход метода Гаусса.
Так как в равенстве 3=41
43
−
⋅
+
⋅
−
xx
имеются два неизвестных, то одно
из этих неизвестных объявим параметром. Пусть, например,
tx
=
4
---
параметр. Тогда из предыдущего равенства следует, что 34=
3
+
tx
.
Далее находим:
2
11
x
⋅
−
3
10
x
⋅
+
4
51
x
⋅
−
63
=
⇒
2
11
x
⋅
−
3)
(4
10
+
⋅
+
t
t
⋅
−
51
63
=
3=
2
−
−
⇒
tx
.
1
2
x
⋅
2
7
x
⋅
+
3
8
x
⋅
−
4
43
x
⋅
+
49
=
−
⇒
1
2
x
⋅
3)
(
7
−
−
⋅
+
t
3)
(4
8
+
⋅
−
t
t
⋅
+
43
49
=
−
22=
1
−
−
⇒
tx
.
Ответ:
22=
1
−
−
tx
; 3=
2
−
−
tx
; 34=
3
+
tx
;
tx
=
4
;
t
--- параметр.
Метод Гаусса можно применять для решения любой системы линейных
алгебраических уравнений, в частности, для решения переопределеных систем

24
(т.е. систем уравнений, в которых число неизвестных меньше числа уравнений)
и систем уравнений, в которых число неизвестных больше числа уравнений.
Приведём примеры 6 и 7 решения переопределенной системы уравнений.
Пример 6.
Найти все решения следующей системы уравнений:
−−+−
+−
++
−−−
59=3589
48=3068
13=1927
10=1176
321
321
321
321
xxx
xxx
xxx
xxx
Решение:
Прямой ход метода Гаусса.
−−−
−
−
−
−
59|3589
48|3068
13|1927
| 101176
6
7
−
−
6
8
−
−
6
9
−
−
−−
−
−
444|1111110
368|92920
148|37370
Делим элементы строки 1 на 37
Делим элементы строки 2 на 92
Делим элементы строки 3 на 111
−
−−
−
−
4|110
4|110
| 4110
1
1
−
1
1
Так как в процессе прямого хода метода Гаусса получили матрицу вида:
0|000
0|000
то прямой ход закончен и начинаем обратный ход, причем начинаем его с
последней выделенной (подчеркнутой) строки, в которой есть хотя бы один не
нулевой элемент.
Обратный ход метода Гаусса.
Так как в равенстве 4=11
32
−
⋅
−
⋅
xx
имеются два неизвестных, то одно из
этих неизвестных объявим параметром. Пусть, например,
tx
=
3
--- параметр.
Тогда из предыдущего равенства следует, что 4=
2
−
tx
.
Далее находим:
1
6
x
⋅
−
2
7
x
⋅
−
3
11
x
⋅
−
10
=
⇒
1
6
x
⋅
−
4)
(
7
−
⋅
−
t
t
⋅
−
11
10
=
33=
1
+
−
⇒
tx
.
Ответ:
33=
1
+
−
tx
; 4=
2
−
tx
;
tx
=
3
;
t
--- параметр.

25
Пример 7.
Найти все решения следующей системы уравнений:
+−−
+−−
+−−
−++−
19=364
21=789
28=295
10=423
321
321
321
321
xxx
xxx
xxx
xxx
Решение:
Прямой ход метода Гаусса.
−−
−−
−−
−
−
19|364
21|789
28|295
| 10423
3
5
−
3
9
−
3
4
−
−
−
−
97|7260
153|15420
134|14370
Делим элементы строки 2 на 3
−
−
−
97|7260
134|14370
| 515140
14
37
−
14
26
−
−− 32|3200
11|1100
Делим элементы строки 1 на 11
Делим элементы строки 2 на 32
−− 1|100
| 1100
1
1
Так как в процессе прямого хода метода Гаусса получили матрицу вида:
(
)
0|000
то прямой ход закончен и начинаем обратный ход, причем начинаем его с
последней выделенной (подчеркнутой) строки, в которой есть хотя бы один не
нулевой элемент.
Обратный ход метода Гаусса.
Из равенства 1=1
3
x
⋅
следует, что 1=
3
x
.
Далее находим:
2
14
x
⋅
3
5
x
⋅
+
51
=
−
⇒
2
14
x
⋅
(1)
5
⋅
+
51
=
−
4=
2
−
⇒
x
.
1
3
x
⋅
−
2
2
x
⋅
+
3
4
x
⋅
+
10
=
−
⇒
1
3
x
⋅
−
4)
(
2
−
⋅
+
(1)
4
⋅
+
10
=
−
2=
1
x
⇒
.
Ответ:
2=
1
x
; 4=
2
−
x
; 1=
3
x
.

26
В заключение приведем пример решения системы уравнений, в которой
количество неизвестных больше числа уравнений.
Пример 8.
Найти все решения следующей системы уравнений:
+++−
−−−−−
−
−
−
−
8=54684
6=3728
11=27432
4321
4321
4321
xxxx
xxxx
xxxx
Решение:
Прямой ход метода Гаусса.
−
−−−−−
−
−
−
−
8|54684
6|3728
| 1127432
2
8
2
4
−−
−
−
−
−
28|0440
100|22246280
Делим элементы строки 1 на 2
Делим элементы строки 2 на 4
−−−−
−
−
50|11123140
| 70110
1
14
Так как в процессе прямого хода метода Гаусса получили матрицу вида:
(
)
148|1113700
−
−
−
то прямой ход закончен и начинаем обратный ход.
Обратный ход метода Гаусса.
Так как в равенстве 148=11137
43
−
⋅
−
⋅
−
xx
имеются два неизвестных, то
одно из этих неизвестных объявим параметром. Пусть, например,
tx
=
4
---
параметр. Тогда из предыдущего равенства следует, что 43=
3
+
−
tx
.
Далее находим:
2
1
x
⋅
3
1
x
⋅
−
7
=
−
⇒
2
1
x
⋅
4)
3
(
1
+
−
⋅
−
t
7
=
−
33=
2
−
−
⇒
tx
.
1
2
x
⋅
2
3
x
⋅
−
3
4
x
⋅
−
4
27
x
⋅
−
11
=
−
⇒
1
2
x
⋅
3)
3
(
3
−
−
⋅
−
t
4)
3
(
4
+
−
⋅
−
t
t
⋅
−
27
11
=
−
23=
1
−
⇒
tx
.
Ответ:
23=
1
−
tx
; 33=
2
−
−
tx
; 43=
3
+
−
tx
;
tx
=
4
;
t
--- параметр.
Задачи для самостоятельного решения.
1. Решить следующие системы линейных алгебраических уравнений тремя
способами (методом Гаусса, методом Крамера, матричным методом):
а)
5 3 5 12,
7 5 7 20,
8 3 9 14,
x y z
x y z
x y z
− + + =
− − = −
− − = −
б)
8 5 7 7,
3 4 6 22,
7 4 5 30,
x y z
x y z
x y z
− − =
+ − =
+ + = −
в)
3 4 7 4,
9 2 6 8,
4 7 9 19,
x y z
x y z
x y z
− − − = −
+ + = −
− + + =
27
г)
6 3 8 12,
2 7 6 54,
2 9 8 68,
x y z
x y z
x y z
− − + = −
− + − =
− + − =
д)
2 3 3 4,
3 5 2 25,
5 9 3 44,
x y z
x y z
x y z
− − + =
− + + = −
− − =
е)
4 3 7 38,
5 2 4 8,
7 4 9 56,
x y z
x y z
x y z
− + + = −
+ + =
− + + = −
ж)
9 5 8 5,
7 4 6 4,
9 9 4 13
x y z
x y z
x y z
− + + = −
− + + = −
− − =
.
2. Решить матричное уравнение
A X B
⋅ =
, где А,В,Х – матрицы, если
а)
7 4
3 1
A
−
=
−
,
28 9
9 1
B
=
; б)
2 3
5 4
A
=
,
4 7
3 7
B
−
=
−
;
в)
3 2
4 3
A
−
=
,
10 11
2 9
B
=
; г)
2 3 3
3 5 2
5 9 3
A
− −
= −
− −
,
11 9 13
9 8 12
14 15 19
B
− −
= −
− −
;
д)
4 7 7
5 3 7
4 3 6
A
− −
= − −
− −
,
20 25 18
10 26 15
10 22 13
B
−
= −
−
; е)
3 4 9
4 5 8
3 4 5
A
−
=
−
,
6 38 10
47 10 13
14 26 10
B
−
=
−
;
ж)
4 7 5
5 8 2
3 5 3
A
= − −
,
34 6 17
23 15 4
23 5 11
B
= − − −
.
3. Найти решения следующих систем уравнений:
а)
2 3 4 13,
2 5 2 3,
2 2 3 6,
3 3 4 8,
x y z
x y z
x y z
x y z
− + =
− + + = −
− − + =
+ − = −
б)
4 3 2 15,
4 5 1,
3 2 6,
2 4 3 14,
x y z
x y z
x y z
x y z
− − + = −
+ + = −
+ + =
+ − =
в)
3 3 2 0,
2 4 3 13,
7 7 4 2,
5 2 2 4,
x y z
x y z
x y z
x y z
− + − =
− + + =
− + = −
− + = −
г)
5 2 3 4,
3 3 1,
2 0,
6 3 4 5,
x y z
x y z
x y z
x y z
+ + =
− + + = −
− + + =
+ + =
д)
2 3 2 5 8,
5 2 5 3 3,
3 7 3 4 11,
x y z w
x y z w
x y z w
− + − = −
− − − + =
+ + + =
е)
4 4 3 2 1,
3 2 2 4 3,
5 7 4 3 5,
x y z w
x y z w
x y z w
− + − = −
− − − = −
− + − + =
ж)
2 3 6 4 11,
3 4 10 2 9,
4 3 8 3 5,
x y z w
x y z w
x y z w
+ − − =
− + + − =
− − + = −
з)
4 8 3 2 8,
3 2 4 3 11
2 5 7 2 7,
x y z w
x y z w
x y z w
+ + − =
+ − + =
− + + + =
и)
3 2 4 4 7,
2 4 5 3 1,
4 3 3 2 6,
3 4 3 3 0,
x y z w
x y z w
x y z w
x y z w
+ + + =
+ + − = −
+ + + = −
+ + − =
к)
2 3 4 5 3,
3 2 2 4 2,
5 2 3 2 5,
4 9 5 3 26
x y z w
x y z w
x y z w
x y z w
+ + + =
+ + + =
− − + − =
− + + =
.

28
2. ВЕКТОРНАЯ АЛГЕБРА
Вектором
называется направленный отрезок.
Обозначения: a,
a
,
AB
. Длина этого отрезка называется
модулем вектора
и
обозначается |a| ,
ABa
,
Векторы называются
коллинеарными
, если они лежат на одной прямой или
на параллельных прямых.
Векторы называются
компланарными,
если они лежат в одной плоскости
или на параллельных плоскостях.
Вектор называется
нулевым,
если его начальная и конечная точки
совпадают. Нулевой вектор не имеет определенного направления и считается
коллинеарным и перпендикулярным любому вектору.
Два вектора называются
равными
, если они коллинеарны, имеют
одинаковую длину (модуль) и одинаковое направление.
Суммой
a
+
b
векторов
a
и
b
называется вектор,
идущий из начала вектора
a
в конец вектора
b
, если
начало вектора
b
совпадает с концом вектора
a
.
Такое правило сложения векторов называют
правилом
треугольника.
Свойства сложения:
1.
a
+
b
=
b
+
a
.
2. (
a
+
b
)+
c
=
a
+(
b
+
c
).
3. Для любого вектора
a
существует нулевой вектор
0
такой, что
a
+
0
=
a
.
4. Для каждого вектора
a
существует противоположный ему вектор -
a
такой,
что
a
+
(-
a
)=
0
.
Произведением
k
a
вектора
a
на число
k
называется вектор
b
,
коллинеарный вектору ,
a
имеющий модуль, равный |
k
||
a
|, и направление,
совпадающее с направлением
a
при
k
>0 и противоположное
a
при
k<0.
Свойства умножения вектора на число:
1.
k(
a
+
b
) = k
a
+ k
b
.
2. (
k + m)
a
= k
a
+ m
a
.
3.
k(m
a
) = (km)
a
.
Если ненулевые векторы
a
и
b
коллинеарны, то существует такое число
k
,
что
b
=
k
a
.
Разностью
векторов
a
и
b
называется вектор
a
–
b
=
a
+(–1)
·
b
Линейной комбинацией
векторов
a
1,
a
2
,…,
a
n
называется выражение вида:
k
1
a
1
+ k
2
a
2
+…+ k
n
a
n,
,
где
k
i
– действительные числа.
b
a
ba +

29
Векторы
a
1,
a
2
,…,
a
n
называются
линейно зависимыми
, если найдутся такие
числа
k
1
, k
2
,…, k
n
, не все равные нулю, что соответствующая линейная
комбинация векторов равна нулю, т.е.
k
1
a
1
+ k
2
a
2
+…+ k
n
a
n
=
0
. (1)
Если же равенство (1) возможно только при всех
k
i
= 0, то векторы называются
линейно независимыми.
Свойства линейной зависимости векторов
:
1. Если система векторов содержит нулевой вектор, то она линейно зависима.
2. Если среди
n
векторов какие-либо (
n
-1) линейно зависимы, то и все n
векторов линейно зависимы.
3. Любые три вектора на плоскости линейно зависимы.
4. Любые четыре вектора в трехмерном пространстве линейно зависимы.
Базисом
на плоскости (в пространстве) называются два (три) любых
линейно независимых вектора.
Любой вектор плоскости (пространства) может быть представлен в виде
линейной комбинации базисных векторов. Числовые коэффициенты этой
линейной комбинации называются
координатами
данного вектора в
рассматриваемом базисе. Если
a
,
b
,
c
– базис и
d
=
k
a
+ m
b
+ p
c
, то числа
k,
m, p
есть координаты вектора
d
в базисе
a
,
b
,
c
.
Представление вектора в виде линейной комбинации базисных векторов
называется разложением вектора
d
в базисе векторов
a
,
b
,
c
и обозначается
символически
d
=
{
k; m; p
}.
Свойства базиса:
1.
Разложение вектора по данному базису единственно, т.е. его координаты
в этом базисе определяются единственным образом.
2.
При сложении двух векторов их координаты в данном базисе
складываются.
3.
При умножении вектора на число все его координаты умножаются на это
число.
4.
Проекцией
вектора
АВ
на ось u
называется положительное число
ВА
′′
,
если направления вектора
В
А
′′
и
направление оси u совпадают и
отрицательное число -
ВА
′′
, если вектор
В
А
′′
и ось u противоположно
направлены. Точки
А’
и
B’
являются
основаниями перпендикуляров,
опущенных из точек А и В на ось u.
Проекция вектора
a
=
АВ
на ось u обозначается: пр
u
a
, пр
u
АВ
.
B
ϕ
a
a
u
'
A
B
′
A
30
Свойства проекции:
1.
Пр
u
a
= |
a
| cosφ, где φ – угол между
a
и осью u.
2.
При сложении двух векторов их проекции на любую ось складываются.
3.
При умножении вектора на число его проекция на любую ось умножается на
это число.
Три попарно ортогональных единичных вектора
i
,
j
,
k
образуют
декартову систему координат
.
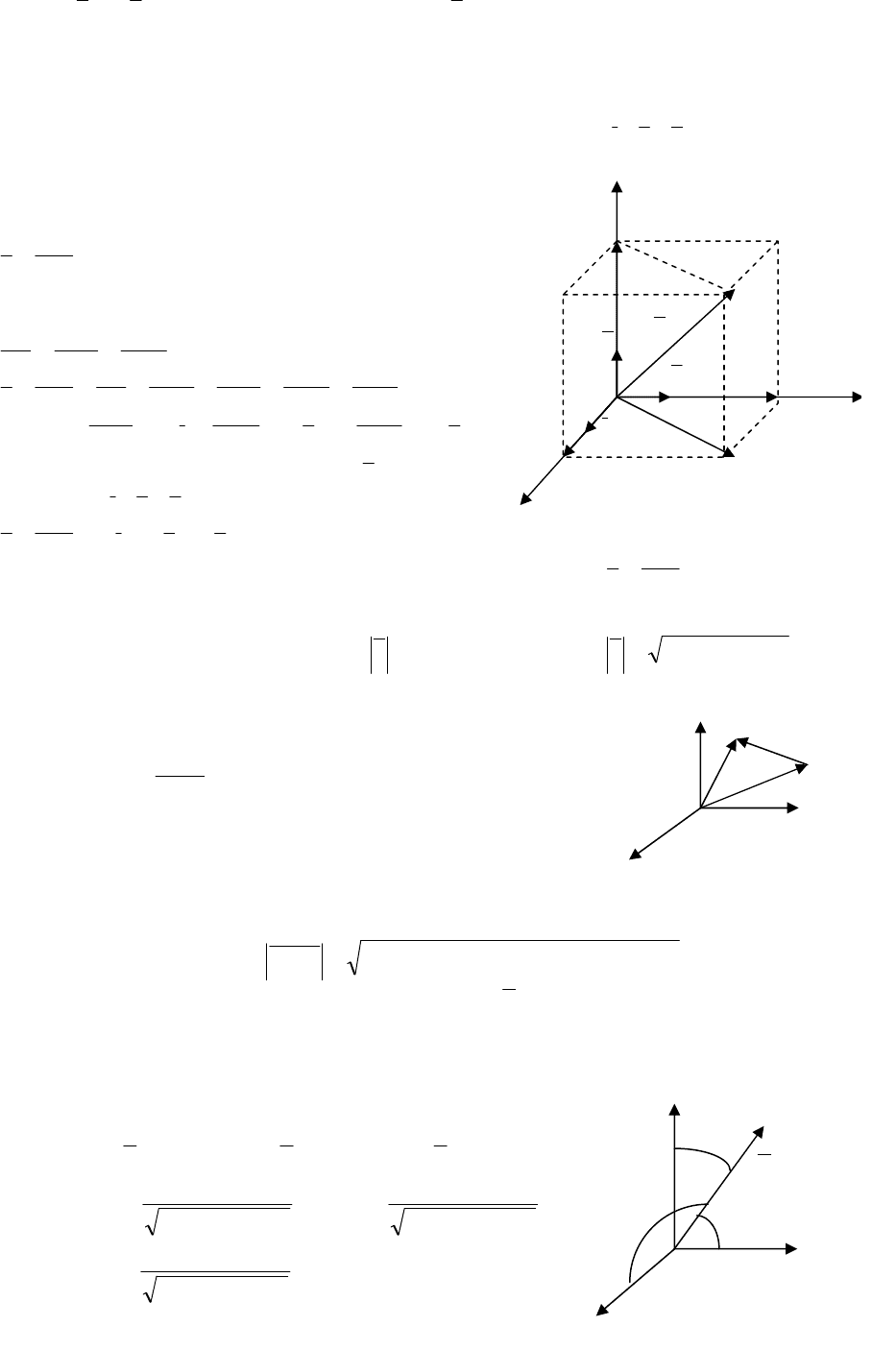
Любой
точке М(X,Y,Z) в пространстве можно
поставить в соответствие радиус-вектор
a
=
ОМ
, имеющий начало в точке О –
начале координат. Используя
определение суммы векторов , получаем
ОP
=
21
ОМОМ +
и радиус-вектор
a
=
ОМ
=
3
ОМОP +
=
321
ОМОМОМ ++
. А
так как
iXОМ =
1
,
jXОМ =
2
и
kXОМ =
3
,
то разложение радиус-вектора
a
в базисе
векторов
i
,
j
,
k
будете иметь вид
a
=
ОМ
=X
i
+Y
j
+Z
k
. Таким образом координаты точки М(X,Y,Z) и
координаты соответствующего ей радиуса-вектора
a
=
ОМ
={X,Y,Z}
совпадают.
Модуль радиуса-вектора равен
222
2
ZYXa ++=
или
222
ZYXa ++=
.
Если вектор в пространстве определяется
начальной точкой N
1
(X
1
,Y
1,
Z
1
) и конечной точкой
N
2
(X
2
,Y
2,
Z
2
), то в координатной форме имеем
21
NN
={X
2
–X
1
; Y
2
-Y
1
; Z
2
-Z
1
}.
Декартовы координаты вектора равны его
проекциям на оси Ох, Оу и Оz декартовой
системы координат.
Расстояние L между точками N
1
(X
1
,Y
1,
Z
1
) и N
2
(X
2
,Y
2,
Z
2
) выражается формулой
( ) ( ) ( )
2
12
2
12
2
1221
ZZYYXXNNL −+−+−==
Косинусы углов, образованных вектором
d
={X,Y,Z} c осями декартовой
системы координат, называются его
направляющими косинусами
.
Свойства направляющих косинусов:
1.
X = |
d
| cos
α
, Y = |
d
| cos
β
, Z = |
d
| cosγ.
2.
222
cos
ZYX
X
++
=
α
,
222
cos
ZYX
Y
++
=
β
,
222
cos
ZYX
Z
++
=
γ
.
3.
cos
2
α + cos
2
β + cos
2
γ = 1.
x
z
N
1
N
2
O
y
d
O
β
α
γ
z
y
x
О
М
a
M
3
(0,0,Z)
M
2
(0,Y,0)
M
1
(X,0,0)
k
i
j
y
z
x
P(X,Y,0)
