Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

31
Условие коллинеарности векторов.
Два ненулевых вектора
a
=a
x
i
+ a
y
j
+ a
z
k
и
b
=b
x
i
+ b
y
j
+ b
z
k
коллинеарны
тогда и только тогда, когда для координат этих векторов справедливы
равенства
z
z
y
y
x
x
b
a
b
a
b
a
==
.
Деление отрезка в заданном отношении.
Пусть даны точки M
1
(X
1
,Y
1,
Z
1
) и M
2
(X
2
,Y
2,
Z
2
). Координаты точки M(X,Y
,
Z),
лежащей на отрезке M
1
M
2
и делящей его в отношении
2
1
MM
MМ
=
λ
равны
λ
λ
+
+
=
1
21
XX
X
,
λ
λ
+
+
=
1
21
YY
Y
,
λ
λ
+
+
=
1
21
ZZ
Z
.
Если точка M(X,Y
,
Z) делит отрезок M
1
M
2
пополам, то
λ
= 1 и её координаты
определятся по формулам
2
21
XX
X
+
=
,
2
21
YY
Y
+
=
,
2
21
ZZ
Z
+
=
.
Скалярное произведение векторов.
Скалярным произведением
двух векторов называется число равное
произведению модулей векторов на косинус угла между ними
a b
= |
a
|
·
|
b
|
·
cosφ.
Обозначения скалярного произведения:
a b
, (
a
,
b
),
a
·
b
.
Скалярное произведение векторов связаны с их проекциями
a b
= |
a
| пр
a
b
= |
b
| пр
b
a
.
Свойства скалярного произведения:
1.
a b
=
b a
.
2. (
k
a
)
b
= k(
a
,
b
).
3. (
a
+
b
)
c
=
a c
+
b c
.
4.
a
2
=
a a
= |
a
|
2
, где
a
2
называется скалярным квадратом вектора
a
.
Приложения скалярного произведения:
1. Если векторы
a
и
b
определены своими декартовыми координатами
a
={X
1
, Y
1
, Z
1
},
b
={X
2
, Y
2
, Z
2
}, то:
1.
a b
= X
1
X
2
+ Y
1
Y
2
+ Z
1
Z
2
.
2. cosφ =
2
2
2
2
2
2
2
1
2
1
2
1
212121
ZYXZYX
ZZYYXX
++⋅++
++
.
3. пр
a
b
=
2
1
2
1
2
1
212121
ZYX
ZZYYXX
++
+
+
, пр
b
a
=
2
2
2
2
2
2
212121
ZYX
ZZYYXX
++
+
+
.
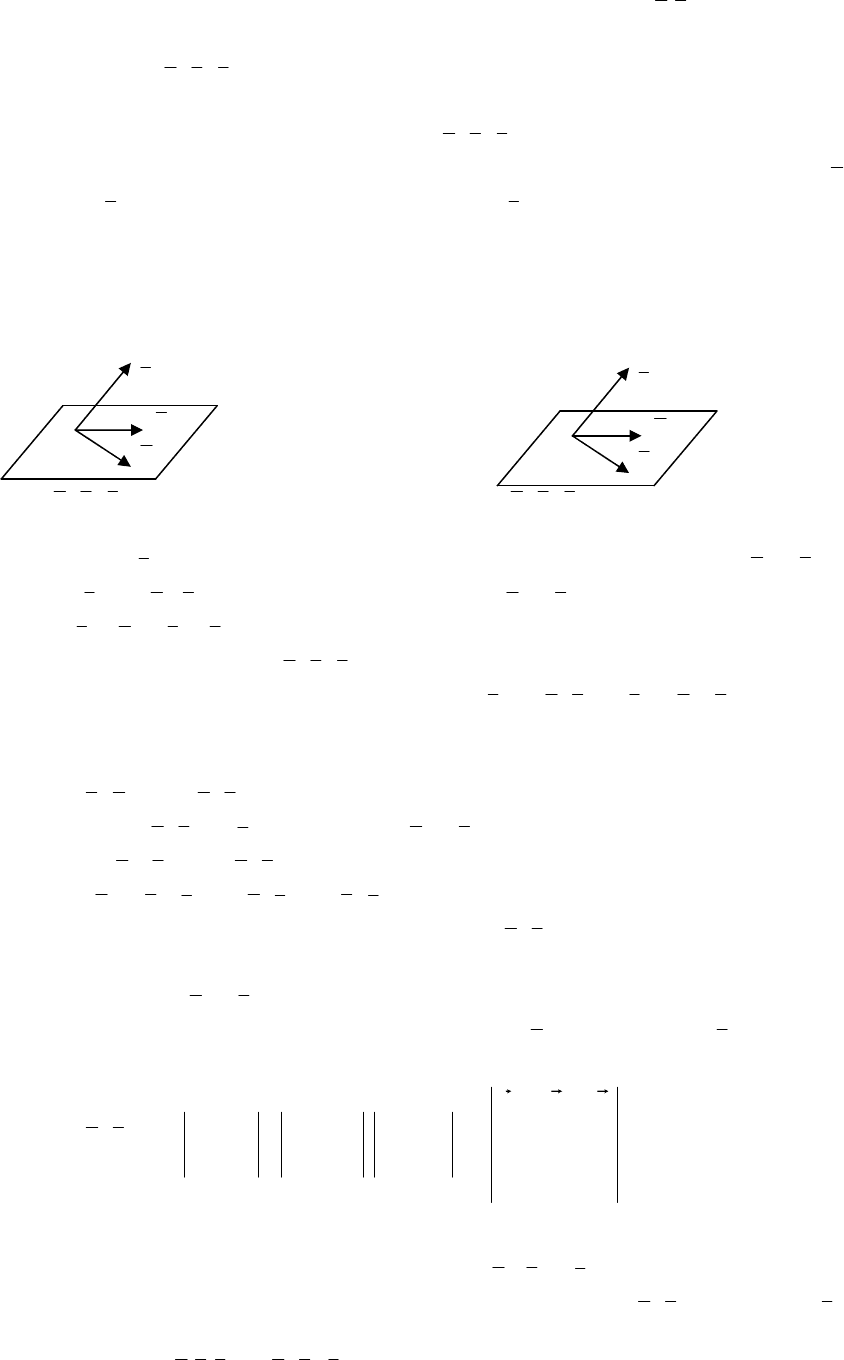
32
Условие перпендикулярности векторов:
Для того чтобы векторы были
перпендикулярными необходимо и достаточно чтобы
a b
= 0.
Векторное произведение векторов.
Векторы
a
,
b
,
c
, для которых определен порядок следования называются
упорядоченной тройкой векторов.
Тройка некомпланарных векторов
a
,
b
,
c
называется
правой (левой),
если
после приведения к общему началу кратчайший поворот от вектора
a
к
вектору
b
, наблюдаемый с конца вектора
c
, виден совершающимся против (по)
часовой стрелке.
a
,
b
,
c
– правая тройка
a
,
b
,
c
– левая тройка
Вектор
c
называется
векторным произведением
векторов
a
и
b
, если:
1.
|
c
| = |
a
||
b
|sinφ, где φ – угол между
a
и
b
.
2.
c
⊥
a
и
c
⊥
b
.
3.
Тройка векторов
a
,
b
,
c
является правой.
Обозначения векторного произведения:
c
= [
a
,
b
],
c
=
a
×
b
.
Свойства векторного произведения.
1.
[
b
,
a
] = - [
a
,
b
].
2.
Если [
a
,
b
] =
0
, то векторы
a
и
b
коллинеарны.
3.
[(k
a
),
b
] = k[
a
,
b
].
4.
[(
a
+
b
),
c
] = [
a
,
c
] + [
b
,
c
].
5.
Модуль векторного произведения |[
a
,
b
]| равняется площади S
параллелограмма, построенного на приведенных к общему началу
векторах
a
и
b
.
6.
Если в декартовой системе координат
a
={X
a
, Y
a
, Z
a
},
b
={X
b
, Y
b
, Z
b
}, то
[
a
,
b
] =
.,,
bbb
aaa
bb
aa
bb
aa
bb
aa
ZYX
ZYX
kji
YX
YX
ZX
ZX
ZY
ZY
=
−
Смешанное произведение векторов.
Смешанным произведением
векторов
a
,
b
и
c
называется результат
скалярного произведения векторного произведения [
a
,
b
] на вектор
c
.
Обозначение:
a b c
= [
a
,
b
]
c
.
b
a
c
a
b
c
33
Свойства смешанного произведения.
1.
Смешанное произведение [
a
,
b
]
c
равно +V- объему параллелепипеда,
построенного на приведенных к общему началу векторах
a
,
b
,
c
, если они
образуют правую тройку или –V, если
a
,
b
,
c
– левая тройка.
Если
a
,
b
и
c
компланарны, то [
a
,
b
]
c
= 0.
2.
a b c
=
b c a
=
c a b
.
3.
a b c
= -
b a c
.
4.
Если
a
= {X
a
, Y
a
, Z
a
},
b
= {X
b
, Y
b
, Z
b
},
c
= {X
c
, Y
c
, Z
c
}, то
a b c
=
ccc
bbb
aaa
ZYX
ZYX
ZYX
.
Пример 1. Даны вершины
А
(0,2),
В
(4,1),
С
(-2,-3), треугольника
АВС
.
Найти: а) длину медианы
АE
; б) внутренний угол
С
.
а) Для нахождения длинны медианы
АЕ
используем формулу расстояния
между двумя точками:
2 2
( ) ( )
E A E A
AE x x y y= − + −
.
Координаты точки
Е
найдем по формулам координат середины отрезков:
1 1
( ), (4 2) 1
2 2
Е В С Е
x x x x
= + = − =
;
1 1
( ), (1 3) 1
2 2
Е В С Е
y y y y
= + = − = −
;
Е
(1; -1), тогда
2 2
(1 0) ( 1 2) 10
AE = − + − − =
.
б) Внутренний угол
С
треугольника
АВС
образован векторами
и
СА СВ
.
Используя формулу косинуса угла между векторами
cos
CA CB
C
CA CB
⋅
∠ =
⋅
, определим
угол
С.
Найдем координаты и длины векторов
и
СА СВ
:
{ }
{ }
.1345246},4;6{)3(1);2(4
,512},1;2{)3(2);2(0
22
22
==+==−−−−=
=+==−−−−=
CBCB
CACA
Скалярное произведение векторов
и
СА СВ
равно:
2 6 1 4 16,
СА СВ
= ⋅ + ⋅ =
⋅
тогда
16 4 4
, .
5 13 65 65
cos arccos
4
C C
=
∠ = ∠ =
⋅
Пример 2
. Даны векторы
a
={ 0; -5; -1},
b
={ -2; 2; -1} и
c
={ 3; -5; 0}.
Вычислите:
а) скалярное произведение
b
,
c
;
34
б) модуль векторного произведения векторов
a
,
b
;
в) смешанное произведение векторов
a
,
b
и
c
. Проверьте: г) будут ли
коллинеарны или ортогональны какие-либо два из трех заданных векторов;
д) будут ли компланарны три заданных вектора.
а) Найдем скалярное произведение векторов
b
и
c
:
2 3 2 ( 5) ( 1) 0 16
bc
= − ⋅ + ⋅ − + − ⋅ = −
.
б) Чтобы вычислить
,
b
а
, найдем координаты векторного произведения
,
а b
:
( ) ( ) ( )
,
5 1 0 1 0 5
0 5 1
2 1 2 1 2 2
2 2 1
5 ( 2) 0 2 0 10 7 2 10 {7; 2; 10}
i j k
а b i j k
i j k i j k
− − − −
= − − = − + =
− − − −
− −
= − − − − + − = + − = −
Тогда
,
2 2 2
7 2 ( 10) 153
а b
= + + − =
.
в) Смешанное произведение векторов
a
,
b
и
c
найдем по формуле:
0 5 1
2 2 1
3 5 0
аbс
− −
= − −
−
,
вычислив определитель третьего порядка, получим
a
b
c
= 11.
г) Два вектора коллинеарны, если их координаты пропорциональны или
векторное произведение равно нулевому вектору. Из б) следует, что
,
а b
≠
0
,
следовательно векторы
a
и
b
не коллинеарны.
Проверим коллинеарность векторов
a
и
c
,
b
и
c
:
0 5 1
3 5 0
− −
≠ ≠
−
, следовательно
векторы
a
и
c
не коллинеарны.
2 2 1
3 5 0
− −
≠ ≠
−
, следовательно векторы
b
и
c
не
коллинеарны.
Из а) следует, что векторы
b
и
c
не ортогональны, т.к. скалярное
произведение этих векторов не равно нулю. Найдем скалярные произведения
векторов
a
c
и
a
b
:
0 3 ( 5) ( 5) ( 1) 0 25 0
ac
= ⋅ + − ⋅ − + − ⋅ = ≠
,
0 ( 2) ( 5) 2 ( 1) ( 1) 9 0
ab
= ⋅ − + − ⋅ + − ⋅ − = − ≠
.
Это значит что векторы
a
и
c
,
a
и
b
не ортогональны.
д) Условием компланарности трех векторов является равенство нулю их
смешанного произведения. Из в) следует, что
a
b
c
≠ 0, это значит, что векторы
a
,
b
и
c
не компланарны.
Пример 3
. Доказать, что векторы
a
={ 1; 3; -1},
b
={ 1; 0; 1} и
c
={ 0; 1; 1}
образуют базис, и найти координаты вектора
d
={ 5; -3; 2} в этом базисе.
Три вектора образуют базис, если они не компланарны, т.е. смешанное
произведение
a
b
c
≠0.
35
Найдем смешанное произведение векторов
a
,
b
и
c
:
5 0
1 3 1
1 0 1
0 1 1
аbс
= − ≠
−
=
, следовательно векторы
a
,
b
,
c
образуют базис.
Обозначим координаты вектора
d
в базисе
a
b
c
через х, у и z. Тогда
d x
а yb zс
= + +
,
или переходя к координатной форме
1 1 0 5
3 0 1 3
1 1 1 2
x y z
+ + = −
−
, получим
5,
3 z = -3,
2.
x y
x
x y z
+ =
+
− + + =
Решая систему методом Крамера, найдем:
1 1 0 5 1 0
, 3 0 1 5, 3 0 1 0, 0
1 1 1 2 1 1
x
x x
x
∆
= ∆ = = − ∆ = − = =
∆
−
;
1 5 0 1 1 5
, 3 3 1 25, 5; , 3 0 3 15, 15.
1 2 1 1 1 2
y
z
y y z z
y z
∆
∆
= ∆ = − = − = = ∆ = − = =
∆ ∆
− −
Таким образом,
d
= 5
b
- 3
c
или
d
={ 0; 5; -3} в базисе
a
b
c
.
Пример 4.
Вершины пирамиды находятся в точках A ( 2; -1;1), B (-2;3;1), C
( 1;2;3) и D ( 1; -2; 2). Вычислите:
а) площадь грани ABC;
б) площадь сечения, проходящего через середину ребра AB и вершины C и
D пирамиды;
в) объем пирамиды ABCD.
а) Площадь треугольника равна половине площади параллелограмма
построенного на тех же векторах, т.е.
,
1
2
ABC
S AB AC
=
.
Найдем координаты векторов
AB
и
AC
:
{
}
{
}
}.2;3;1{13);1(2;21},0;4;4{11);1(3;22
−=−−−−=−=−−−−−= ACAB
Векторное произведение
,
AB AC
равно:
,
2 2 2
, .
4 0 4 0 4 4
4 4 0 8 8 8 (8;8; 8)
3 2 1 2 1 3
1 3 2
1
8 8 ( 8) 192 8 3, 8 3 4 3
2
ABC
i j k
АВ АС i j k i j k
АВ АС S
− −
= − = − + = + − = −
− −
−
= + + − = = = ⋅ =
б) Найдем координаты точки М – середины ребра АВ:
1 1 1
(2 ( 2)) 0; ( 1 3) 1; (1 1) 1,
2 2 2
M M M
x y z
= + − = = − + = = + =
получим М (0; 1; 1).
Площадь треугольника МСD определяется по формуле:
,
1
2
MCD
S MC MD
=
.
Найдем координаты векторов
MC
и
MD
и
,
MC MD
:

36
{
}
{
}
}.1;3;1{12;12;01},2;1;1{13;12;01
−−=−−−−==−−−= MDMC
[ ]
[ ]
.66
2
1
,66)4(17,
},41;7{
31
11
11
21
13
21
131
211,
222
==−++=
−=
−
+−
−
=
−
=
MCD
SMDMC
kji
kji
MDMC
в) Объем пирамиды АВСD вычисляется по формуле:
1
.
6
V
АВ АС АD
=
Координаты векторов
{
}
}.1;1;1{12);1(2;21},2;3;1{},0;4;4{
−−=−−−−−=−=−= ADACAB
Найдем смешанное произведение векторов
4 4 0
1 3 2 24,
1 1 1
AB AC AD
−
= − = −
− −
, тогда
1
24 4.
6
V
= − =
1.
По данным векторам
a
и
b
построить следующие векторы: 1) 2
a
;
2) –0,5
b
; 3) 3
a
+0,25
b
; 4) 0,5
a
-3
b
.
2.
Даны: |
a
|=
13, |
b
|=19 и |
a
+
b
|=
24
.
Вычислить |
a
-
b
|.
3.
Даны: |
a
|=
11, |
b
|=23 и |
a
-
b
|=
30
.
Вычислить |
a
+
b
|.
4.
Даны вершины А(3,2,-5), В(1,4,3) и С(-3,0,1) треугольника. Найти
координаты середин его сторон.
5.
Даны вершины А(2,-1,4), В(3,2,-6) и С(-5,0,2) треугольника. Вычислить
длину медианы, проведенной из вершины А.
6.
Даны три вершины А(3,-1,2), В(1,2,-4) и С(-1,1,2) параллелограмма. Найти
его четвертую вершину D.
7.
Отрезок прямой, ограниченный точками А(-1,8,3) и В(9,-7,2) разделен
точками на пять равных частей. Найти координаты этих точек.
8.
Определить при каких значениях
α
и
β
векторы
a
={-2,3,
β
} и
b
={
α
,-6,2}
коллинеарны.
9.
Проверить, что четыре точки А(3,-1,2), В(1,2,-1), С(-1,1,3) и D(3.-5.3)
служат вершинами трапеции.
10.
Даны два вектора
a
={3,-2,6} и
b
={-2,1,0}. Определить координаты
следующих векторов: 1)
a
+
b
;
2)
a
–
b
; 3) 2
a
;
4)2
a
+3
b
; 5) 0,5
a
-
b
.
11.
Даны два вектора
a
={2,4,3} и
b
={-1,5,8}. Определить координаты
следующих векторов: 1)
a
+
b
;
2)
a
–
b
; 3) 3
a
;
4)
a
+2
b
; 5) 0,5
a
-3
b
.
12.
Найти разложение вектора
x
в базисе векторов
p,q,r,
если
а)
};4,2,1{},1,0,1{},2,1,0{},7,4,2{
−
=
=
=
−
=
rqpx
б)
};2,1,0{},1,1,2{},0,3,1{},1,12,6{
−
=
−
=
=
−
=
rqpx
в)
};1,1,1{},2,3,0{},1,1,2{},4,4,1{
−
=
=
−
=
−
=
rqpx
г)
}.1,2,1{},3,0,2{},1,1,4{},5,5,9{
−
=
−
=
=
−
=
rqpx
13.
Выяснить, будут ли векторы
а
1
={1,1,1,1},
а
2
={1,2,1,2},
а
3
={3,1,3,1},
а
4
={0,1,0,1} линейно зависимыми или линейно независимыми.
37
14.
Доказать, что система векторов, содержащая два равных вектора, линейно
зависима.
15.
Найти все значения
λ
, при которых вектор
b
={7,-2,
λ
} линейно выражается
через векторы
а
1
={2,3,5},
а
2
={3,7,8},
а
3
={1,-6,1}.
16.
Векторы
a
и
b
образуют угол
3
π
ϕ
=
; зная, что |
a
|
=3 и |
b
|=4, вычислить: 1)
a b
;
2)
a
2
; 3)
b
2
; 4) (
a
+
b
)
2
; 5) (3
a
+2
b
)(
a
-
b
)
; 6) (
a
-
b
)
2
.
17.
Векторы
a
и
b
образуют угол
3
2
π
ϕ
=
; зная, что |
a
|
=5 и |
b
|=3, вычислить: 1)
a b
;
2)
a
2
; 3)
b
2
; 4) (
a
+
b
)
2
; 5) (3
a
+2
b
)(
a
-
b
)
; 6) (
a
-
b
)
2
.
18.
Даны векторы
a
={4,-2,-4} и
b
={6,-3,2}. Вычислить: 1)
a b
;
2)
2
a
;
3)
2
b
;
4) (2
a
–
3
b
)(
a
+
b
)
; 5) (
a
+
b
)
2
.
19.
Даны векторы
a
={2,4,4} и
b
={2,-6,3}. Вычислить: 1)
a b
;
2)
2
a
;
3)
2
b
4) (3
a
+
2
b
)(
a
-
b
); 5) (
a
-
b
)
2
.
20.
Даны вершины четырехугольника А(1,-2,2), В(1,4,0), С(-4,1,1) и D(-5,-5,3).
Доказать, что его диагонали АС и ВД взаимно перпендикулярны.
21.
Вычислить проекцию вектора
a
={5,2,5} на ось вектора
b
={2,-1,2} и найти
косинус угла между этими векторами.
22.
Вычислить проекцию вектора
a
={6,3,2} на ось вектора
b
={2,2,1} и найти
косинус угла между этими векторами.
23.
Даны вершины А(-1,-2,4), В(-4,-2,0) и С(3,-2,1) треугольника. Определить
его внутренний угол при вершине В.
24.
Даны три вектора
a
={2,-1,-3},
b
={1,-3,2} и
c
={3,-4,12}. Найти вектор
x
,
удовлетворяющий условиям:
x a
=-5,
x b
=-11,
x c
=20.
25.
Определить и построить вектор
c
=
a
×
b
, если 1)
a
=
3
i
,
b
=
2
k
;
2)
a
=
i
+
j
,
b
=
i
-
j
;
3)
a
=
2
i
+
3
j
,
b
=
3
j
+
2
k
.
26.
Раскрыть скобки и упростить выражения:
1)
i
×
(
j
+
k
) –
j
×
(
i
+
k
) +
k
×
(
i
+
j
+
k
);
2) (
a
+
b
+
c
)
×
c
+
(
a
+
b
+
c
)
×
b
+
(
b
-
c
)
×
a
;
3) (2
a
+
b
)
×
(
c
-
a
) + (
b
+
c
)
×
(
a
+
b
);
4)
2
i
(
⋅
j
×
k
)+ 3
j (
⋅
i
×
k
)+ 4
k
(
⋅
i
×
j
).
27.
Векторы
a
и
b
образуют угол
3
2
π
ϕ
=
; зная, что |
a
|
=1 и |
b
|=2, вычислить: 1)
|
a
×
b
|
2
;
2)
|(3
a
+2
b
)
×
(
a
-
b
)
|
2
; 3) |(
a
+3
b
)
×
(3
a
-
b
)
|
2
.
28.
Даны векторы
a
={3,-1,-2} и
b
={1,-2,-1}. Вычислить: 1)
a
×
b
;
2) (2
a
+
b
)
×
b
; 3) (3
a
+
2
b
)
×
(
a
-
b
).
29.
Даны векторы
a
={1,1,-3} и
b
={3,2,0}. Вычислить: 1)
a
×
b
;
2) (
a
+
3
b
)
×
b
;
3) (
a
+
2
b
)
×
(
a
-
3
b
).
30.
Построить параллелограмм на векторах
a
=
2
j
+
k
и
b
=
i
+
2
k
и вычислить
его площадь и высоту.
31.
Даны вершины А(1,-2,8), В(0,0,4) и С(6,2,0) треугольника. Вычислить его
площадь и длину высоты, опущенной из вершины В на сторону АС.

38
32.
Даны вершины А(1,-1,2), В(5,-6,2) и С(1,3,-1) треугольника. Вычислить его
площадь и длину высоты, опущенной из вершины В на сторону АС.
33.
С помощью векторного произведения выяснить, коллинеарны ли векторы
a
={1,0,3} и
b
={2,0,6}.
34.
Векторы
a
,
b
и
c
,
образующую
правую тройку, взаимно
перпендикулярны. Зная, что |
a
|
=4, |
b
|=2 и |
c
|
=3, вычислить
a b c
.
35.
Вектор
с
перпендикулярен к векторам
a
и
b
,
угол между векторами
a
и
b
равен 30
0
. Зная, что |
a
|
=6, |
b
|=3 и |
c
|
=3, вычислить
a b c
.
36.
Даны три вектора
a
={0,1,-3},
b
={3,2,1},
c
={1,3,2} . Вычислить
a b c
.
37.
Установить, компланарны ли векторы:
1)
a
={2,3,-1},
b
={1,-1,3},
c
={1,9,-11};
2)
a
={1,1,-3},
b
={0,1,0},
c
={1,1,1};
3)
a
={2,-1,2},
b
={1,2,-3},
c
={3,-4,7}.
38.
Доказать, что четыре точки А(1,2,-1), В(0,1,5), С(-1,2,1), D(2,1,3) лежат в
одной плоскости.
39.
Выяснить, будут ли векторы
а
1
={1,0,1},
а
2
={1,1,2},
а
3
={2,1,2} линейно
зависимыми или линейно независимыми.
40.
Вычислить объем пирамиды, вершины которой находятся в точках А(5,2,0),
В(2,5,0), С(1,2,4), D(0,0,0).
41.
Даны вершины пирамиды: А(2,3,1), В(4,1,-2), С(6,3,7), D(-5,-4,8). Найти
длину её высоты , опущенной из вершины D.
39
3. ЭЛЕМЕНТЫ АНАЛИТЕЧЕСКОЙ ГЕОМЕТРИИ
3.1 Прямая на плоскости.
Уравнение прямой на плоскости можно записать в разных видах.
Общее уравнение прямой:
0
=
+
+
C
By
Ax
; (1)
Уравнение прямой, проходящей через точку );(
00
yx с данным нормаль-
ным вектором
{
}
BAN ;= :
0)()(
00
=
−
+
−
yyBxxA ; (2)
Нормальный вектор – ненулевой вектор, перпендикулярный прямой.
Каноническое уравнение прямой (проходящей через точку );(
00
yx , с
данным направляющим вектором
{
}
nms ;= ):
n
yy
m
xx
00
−
=
−
; (3)
Направляющий вектор
– ненулевой вектор, параллельный прямой или
лежащий на прямой.
Уравнение прямой через две данные точки
);(
11
yx
и
);(
22
yx
:
12
1
12
1
yy
yy
xx
xx
−
−
=
−
−
; (4)
Уравнение прямой с данным угловым коэффициентом:
b
kx
y
+
=
, (5)
где
k
угловой коэффициент,
α
tg
k
=
,
α
- угол наклона прямой к поло-
жительному направлению оси абсцисс.
Уравнение прямой, проходящей через точку
);(
00
yx , с данным угловым
коэффициентом
k
:
40
)(
00
xxkyy
−
=
−
. (6)
Условия перпендикулярности и параллельности прямых.
Если прямые
параллельны, то их нормальные, также как и направляющие, векторы колли-
неарны.
Если прямые перпендикулярны, то их нормальные, также как и направ-
ляющие, векторы перпендикулярны.
Условие параллельности двух прямых можно записать и через угловые
коэффициенты. Пусть даны две прямые
111
:
bxkyl
+
=
,
222
:
bxkyl
+
=
.
Две прямые параллельны тогда и только тогда, когда
21
kk
=
,
21
bb
≠
.
Условие перпендикулярности двух прямых
1
21
−=⋅ kk
, угловые коэффи-
циенты перпендикулярных прямых обратны по абсолютной величине и про-
тивоположны по знаку.
Угол между прямыми.
Угол между прямыми может быть найден как
угол между направляющими или нормальными векторами. Например, если
прямые имеют нормальные векторы
{
}
11
1
; BAN = и
{
}
22
2
; BAN = , то косинус
угла
α
между прямыми будет равен
21
21
NN
NN
αсos
rr
r
r
⋅
⋅
= . Если известны угловые
коэффициенты прямых, то
21
12
1 kk
kk
αtg
+
−
= .
Расстояние от точки до прямой. Расстояние от точки );(
00
yx до пря-
мой
0
=
+
+
C
By
Ax
находится по формуле:
22
00
BA
CByAx
d
+
++
=
.
Ниже приведены примеры решения некоторых задач.
.
Пример1.
В треугольнике АВС с вершинами А(2;-2), В(3,1); С(-4;-2)
составить
а) уравнение стороны АВ;
б) уравнение медианы АМ треугольника АВС, проведенной из верши-
ны А;
в) уравнение высоты ВН треугольника АВС, проведенной из вершины
В;
