Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

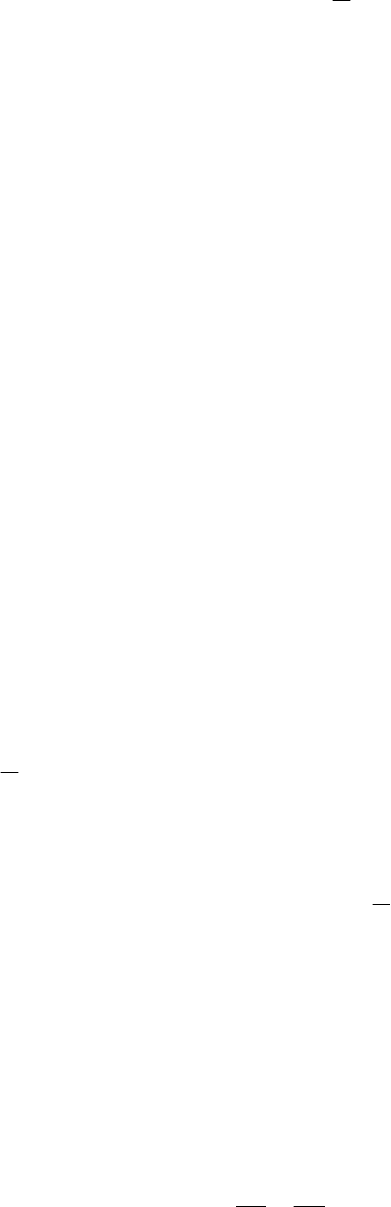
61
длиной 2а и 2в. Величины а и в называют соответственно большой и малой
полуосями эллипса.
Эксцентриситетом эллипса называется отношение
а
с
, где с - половина
расстояния между фокусами эллипса, а - большая полуось эллипса.
Эксцентриситет эллипса принимает значения от 0 до 1 и характеризует
форму эллипса. Чем меньше эксцентриситет, тем больше эллипс похож на
окружность, чем больше эсцентриситет, тем больше эллипс вытянут вдоль
своей большей оси.
Если
в
а
=
, то каноническое уравнение эллипса примет вид
222
ayx
=
+
. Это уравнение окружности радиуса а с центром в начале коор-
динат. Эксцентриситет окружности равен 0.
Оси симметрии гиперболы называют осями гиперболы. Точка пересе-
чения осей симметрии называется центром гиперболы. Одна из осей гипер-
болы пересекает ее в двух точках, которые называются вершинами гипербо-
лы. Эта ось называется действительной осью гиперболы. Другая ось гипер-
болы не имеет с ней общих точек и называется мнимой осью гиперболы.
Прямоугольник со сторонами длиной 2а и 2в, параллельными осям гипербо-
лы и проходящими через ее вершины, называется основным прямоугольни-
ком гиперболы. Его диагонали являются асимптотами гиперболы. В системе
координат, в которой уравнение гиперболы имеет канонический вид, уравне-
ния асимптот имеют вид
х
а
в
у ±= . Величины а и в называют, соответственно
действительными и мнимыми полуосями гиперболы.
Эксцентриситетом гиперболы называется отношение
а
с
, где с - поло-
вина расстояния между фокусами гиперболы, а – действительная полуось ги-
перболы.
Эксцентриситет гиперболы больше 1 и характеризует форму гипербо-
лы. Чем эксцентриситет ближе к 1, тем более вытянута гипербола вдоль дей-
ствительной оси.
Кривая, определяющаяся уравнением
1
2
2
2
2
=+−
b
y
a
x
, также есть ги-
пербола, действительная ось которой 2b, а мнимая 2a. Гиперболы
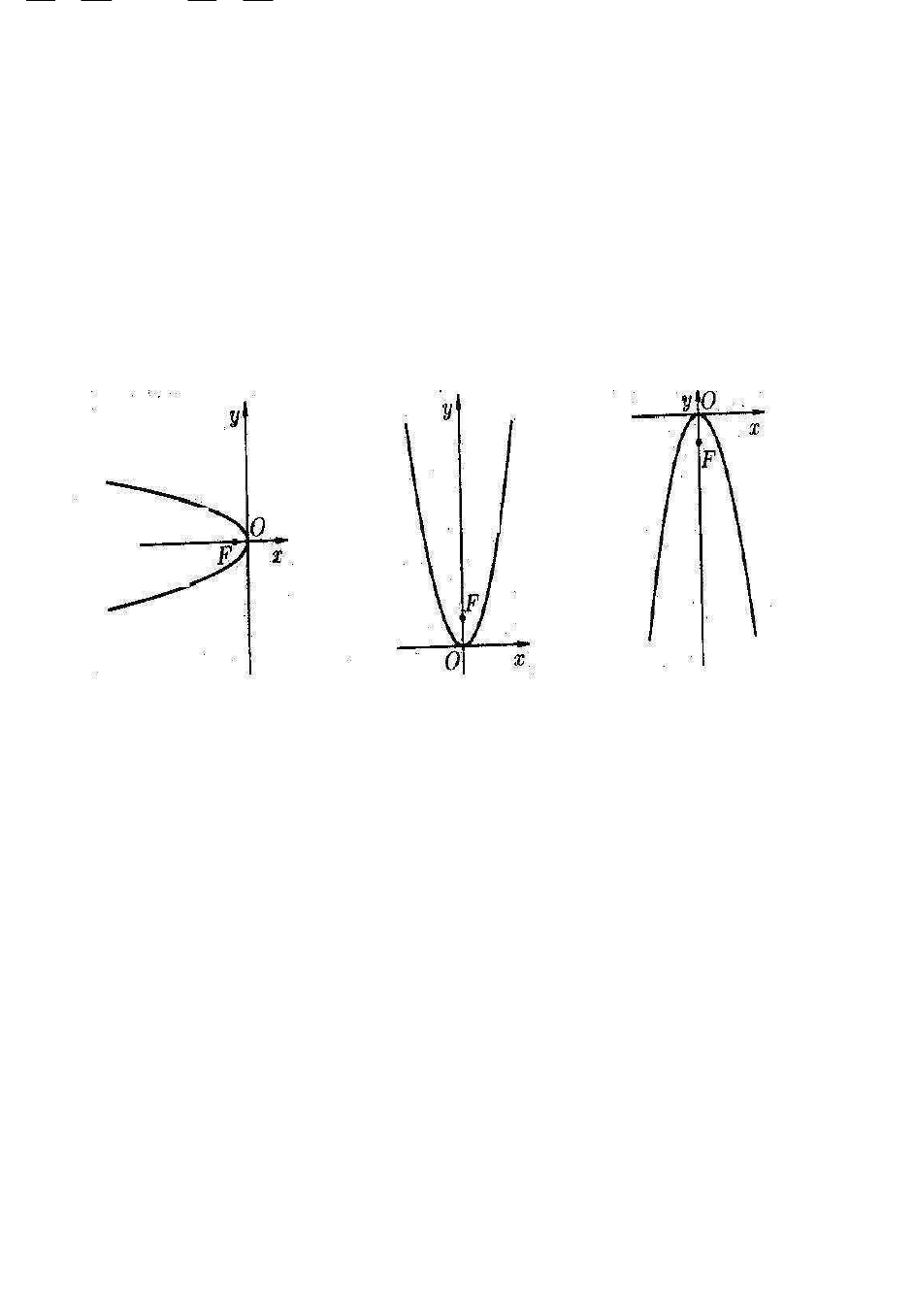
62
1
2
2
2
2
=+−
b
y
a
x
и
1
2
2
2
2
=−
b
y
a
x
имеют общие асимптоты и называются сопряжен-
ными.
Парабола симметрична относительно прямой, проходящей через фокус
параболы, перпендикулярно ее директрисе. Эта прямая называется осью па-
раболы. Вершина параболы лежит на оси параболы и делит расстояние р ме-
жду фокусом и директрисой пополам. Число р, параметр параболы, влияет на
форму параболы, парабола тем шире, чем больше р.
Уравнения pxy 2
2
−
=
, pух 2
2
=
,
pух 2
2
−
=
также определяют парабо-
лы. Они изображены на рисунке.
pxy 2
2
−
=
pух 2
2
=
pух 2
2
−
=
Приведение общего уравнения кривой второго порядка к каноническому
виду. Параллельный перенос системы координат. Пусть на плоскости зада-
ны две декартовы прямоугольные системы координат:
Оxy
(«старая») и yxО
~
~
1
(«новая»), причем как оси абсцисс, так и оси ординат обеих систем парал-
лельны и одинаково направлены.
В этом случае говорят, что одна система координат получается из другой
параллельным переносом.
Пусть начало
1
О «новой» системы координат имеет в «старой» системе
координат координаты );(
11
ух . Связь между «старыми» и «новыми» коорди-
натами точки при параллельном переносе осей координат:
1
~
xxx
−
=
;
1
~
yyy
−
=
.
Пусть некоторая кривая задана уравнением 0);(
11
=
−
−
yyxxf . Тогда в
системе координат
y
x
О
~
~
, полученной параллельным переносом системы
Оxy
,
с началом в точке );(
111
ухО , уравнение кривой будет иметь вид
0
)
~
;
~
(
=
y
x
f
.

63
Уравнение второй степени вида 0
22
=
+
+
+
+
fdyсхbуах (не содержа-
щее члена ху с произведением координат) приводится к каноническому виду
методом выделения полных квадратов. Суть этого метода рассмотрим на
примерах.
Примеры решения задач.
Пример1
. Привести к каноническому виду кривую второго порядка
041849
22
=
+
+
−
+
yxyx . Найти эксцентриситет, координаты фокусов, сде-
лать чертеж.
Решение. Сгруппируем слагаемые с х и слагаемые с у. Коэффициенты
перед
2
x
и
2
y вынесем за скобку.
04)2(9)4(
22
=
+
+
+
−
yyxx
Дополним выражения, стоящие в скобках до полного квадрата.
049)12(94)44(
22
=
+
−
+
+
+
−
+
−
yyxx
9)1(9)2(
22
=
+
+
−
yx
Разделим обе части уравнения на 9.
1
1
)1(
9
)2(
22
=
+
+
− yx
Введем новую систему координат с центром
1
О (2;-1), полученную из
старой параллельным переносом
2
~
−
=
x
x
;
1
~
+
=
y
y
. В новой системе ко-
ординат уравнение примет канонический вид
1
1
~
9
~
22
=+
yx
. Это каноническое
уравнение эллипса с полуосями
3
=
a
,
1
=
b
.
2219
22
=−=−= bac . Координаты фокусов в системе координат
yxO
~
~
1
2
F
(
0;22
) и
)0;22(
1
−F
. Координаты фокусов в системе координат
Оxy
находим по формулам
2
~
−
=
x
x
;
1
~
+
=
y
y
.
)1;222(
1
−+−F
,
)1;222(
2
−+F
.Эксцентриситет
22
3
=
ε
. Чертеж представлен на рисунке.
64
Пример 2.
Привести к каноническому виду кривую второго порядка
01362
2
=
+
−
+
xyx . Найти координаты фокуса, сделать чертеж.
Решение. 01362
2
=
+
−
+
xyx . Сгруппируем слагаемые, содержащие
переменную х и дополним выражение, стоящее в скобках, до полного квадра-
та.
01329)96(
2
=
+
+
−
+
−
yxx
,
042)3(
2
=
+
+
−
yx
.
Запишем уравнение в виде
)2(2)3(
2
+
−
=
−
yx
. Это уравнение парабо-
лы, имеющей вид
yx
~
2
~
2
−
=
в системе координат yxО
~
~
1
, полученной из
Оху
параллельным переносом
3
~
−
=
x
x
,
2
~
+
=
y
y
. Эта парабола симметрична от-
носительно оси
y
О
~
и ее ветви направлены вниз.
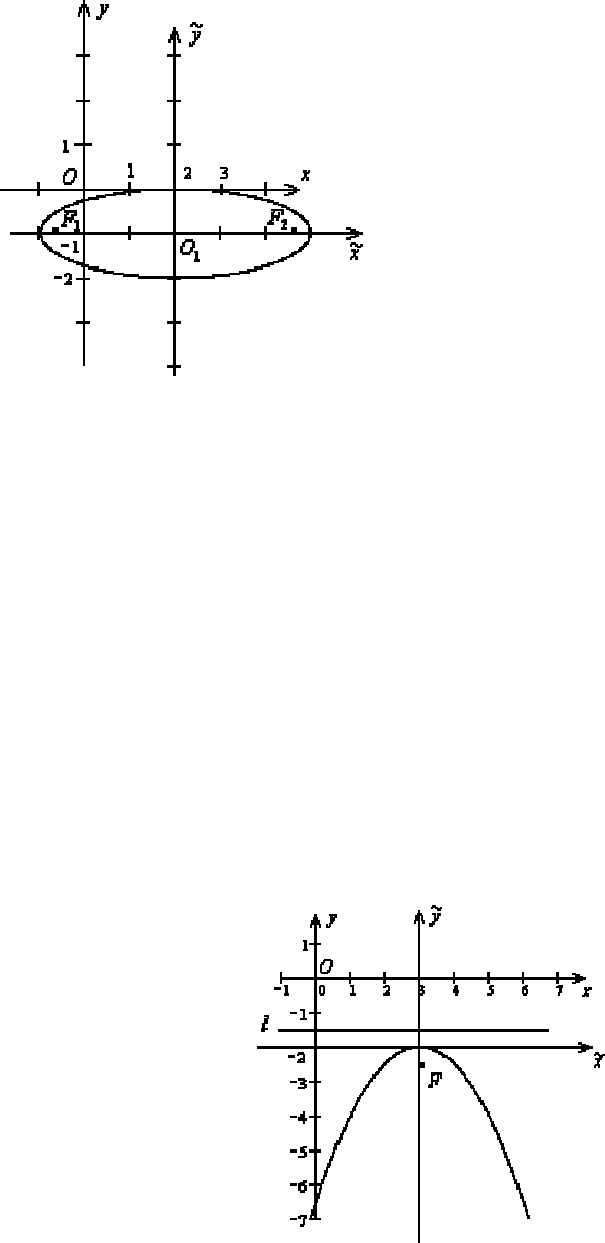
Фокус параболы в «новой» системе координат (-0,5;0). Уравнение ди-
ректрисы
5
,
0
~
=
y
. В «старой» системе координат фокус имеет координаты
(3;-2,5), уравнение директрисы
5
,
1
~
−
=
y
.
65
Задачи для самостоятельного решения.
Привести уравнение линии к каноническому виду, определить тип ли-
нии, найти эксцентриситет, координаты фокусов(а). Изобразить эту ли-
нию.
1.
2 2
4 25 32 150 189 0
x y x y
+ + − + =
.
2.
2 2
4 16 8 160 340 0
x y x y
+ + − + =
.
3.
2
2 6 7 0
x x y
− + + =
.
4.
2
8 8 8 0
x x y
− + − =
.
5.
2 2
36 9 288 18 261 0
x y x y
+ + + + =
.
6.
2 2
16 25 64 100 436 0
x y x y
− − + − =
.
7.
2 2
25 9 200 36 139 0
x y x y
− + − + =
.
8.
2 2
9 9 90 72 0
x y x y
− − + =
.
9.
2 2
9 36 18 216 9 0
x y x y
+ − + + =
.
10.
2 2
4 36 24 288 684 0
x y x y
− − − − =
.
11.
2
4 6 28 0
y y x
− − + =
.
12.
2
8 8 8 0
y y x
+ + + =
.
3.4. Поверхности второго порядка.
Поверхности второго порядка – это поверхности, которые в прямо-
угольной системе координат задаются алгебраическими уравнениями второй
степени.
Поверхность
Каноническое
уравнение
Чертеж
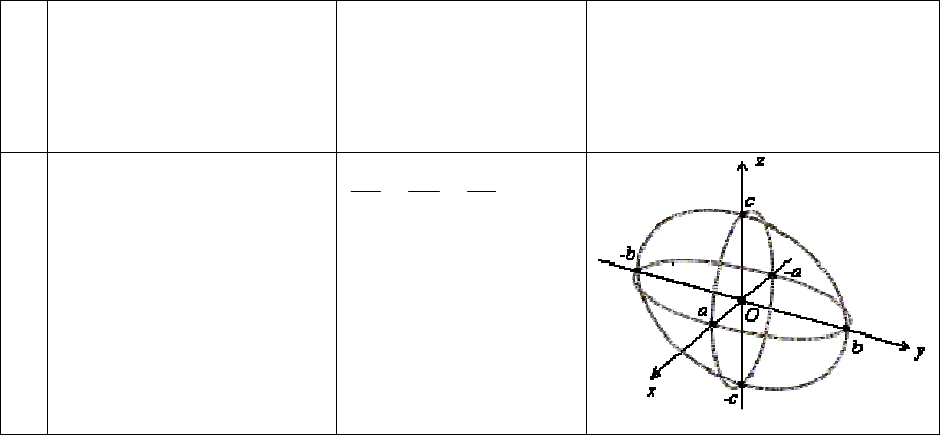
1. эллипсоид
1
2
2
2
2
2
2
=++
c
z
b
y
a
x
66
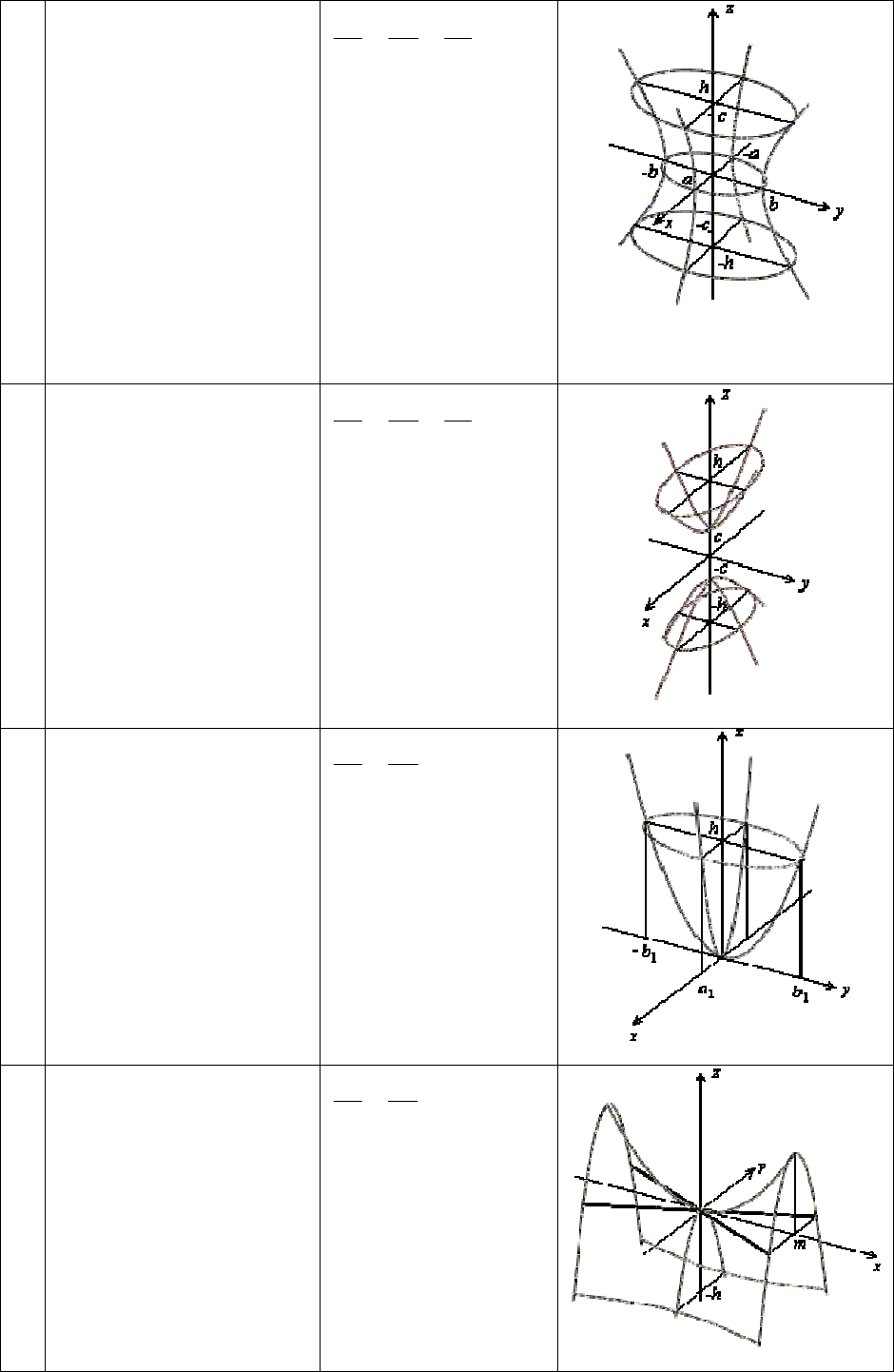
2.
Однополостный ги-
перболоид
1
2
2
2
2
2
2
=−+
c
z
b
y
a
x
3. Двуполостный гипер-
болоид
1
2
2
2
2
2
2
−=−+
c
z
b
y
a
x
4. Эллиптический пара-
болоид
z
b
y
a
x
=+
2
2
2
2
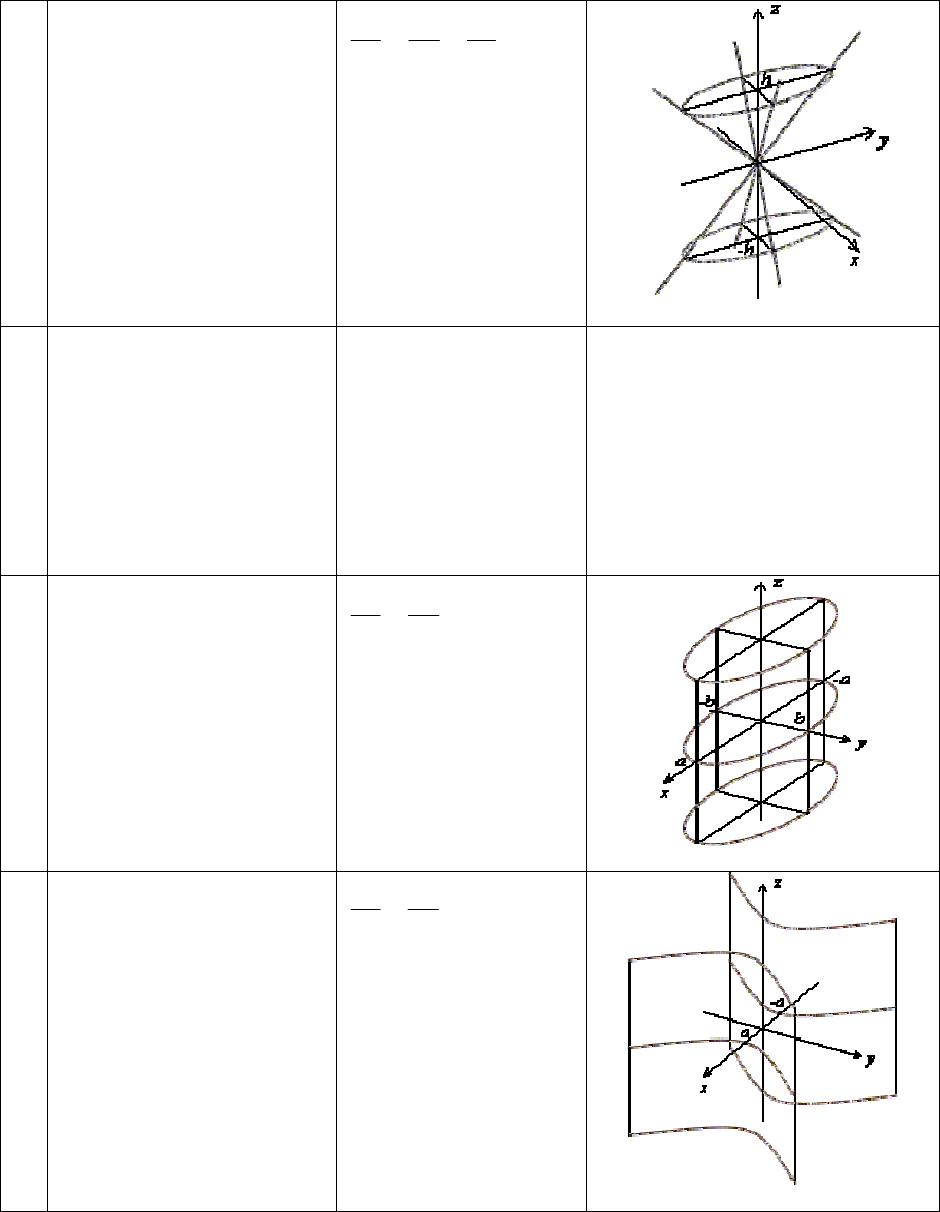
5. Гиперболический па-
раболоид
z
b
y
a
x
=−
2
2
2
2
67
6. Конус
0
2
2
2
2
2
2
=−+
c
z
b
y
a
x
7. Цилиндры Уравнение цилин-
дра, образующая
которого парал-
лельна оси Оz,
имеет вид
0
)
;
(
=
y
x
f
.
а)
Эллиптический ци-
линдр.
1
2
2
2
2
=+
b
y
a
x
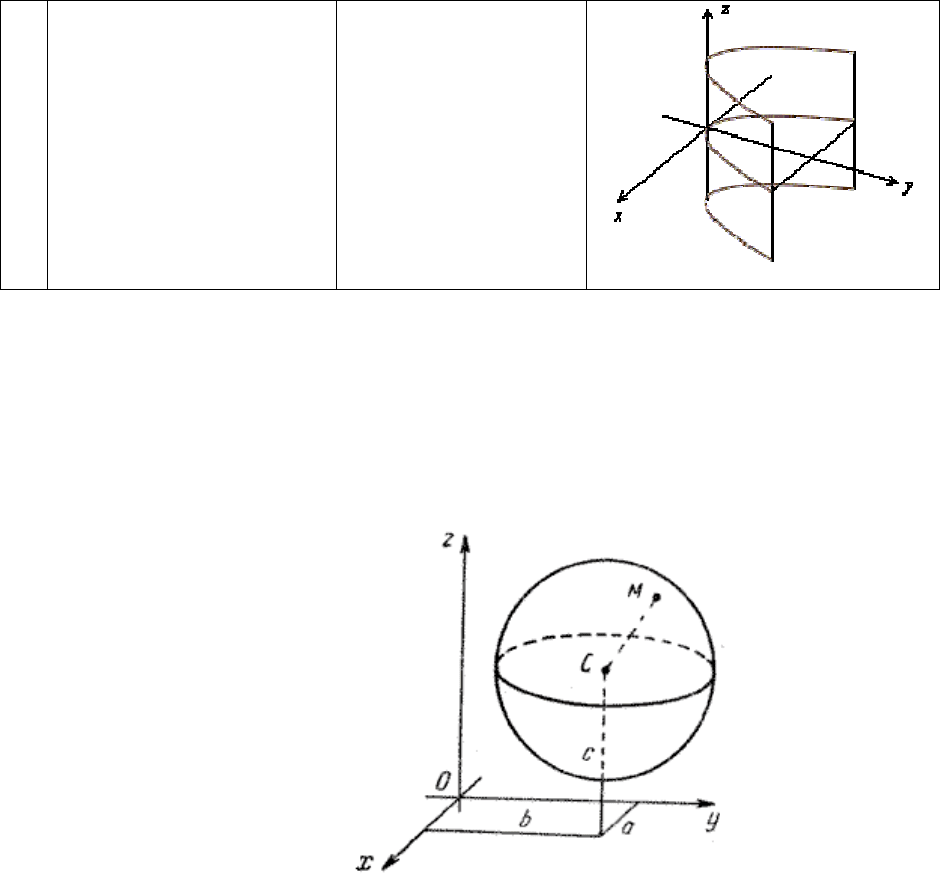
б)
Гиперболический ци-
линдр
1
2
2
2
2
=−
b
y
a
x
68
в)
Параболический ци-
линдр
pxy 2
2
=
Сферой называется множество всех точек пространства, равноуда-
ленных от фиксированной точки, называемой центром.
Уравнение сферы с центром в точке О с координатами (a;b;c) ра-
диуса r имеет вид
2222
)()()( rczbyax
=
−
+
−
+
−
.
Если в каноническом уравнении эллипсоида считать, что a=b=c, то
получим уравнение сферы с центром в начале координат радиуса а.
Примеры решения задач.
Пример 1.
Составить уравнение сферы
а) с центром в точке (-3;2;-4) радиуса 4;
б) с центром в начале координат , касающейся плоскости
0
2
5
3
2
=
+
+
−
z
y
x
.
Решение.
а) Уравнение сферы .16)4()2()3(
222
=
+
+
−
+
+
zyx

69
б) Найдем радиус сферы. Касательная плоскость к сфере перпенди-
кулярна радиусу сферы, проведенному к точке касания. Тогда радиус сфе-
ры равен расстоянию от центра сферы до касательной плоскости. Расстоя-
ние от точки
);;(
000
zyx
до плоскости
0
=
+
+
+
D
Cz
By
Ax
можно
найти по формуле
222
000
CBA
DCzByAx
d
++
+
+
+
= .
5
2
50
2
5)3(4
2
222
==
+−+
=r
.
Уравнение сферы:
25
2
222
=++ zyx .
Пример 2.
Определить координаты центра и радиус сферы
03512
222
=
−
+
−
+
+
zxzyx .
Решение.Преобразуем уравнение сферы следующим образом
03)5()12(
222
=
−
−
+
+
−
zzyxx
,
0325,636)5,2()6(
222
=
−
−
−
+
+
+
−
zyx
,
25,45)5,2()6(
222
=
+
+
+
−
zyx
.
Таким образом, координаты центра сферы (6;0;-2,5),
25,45=r .
Задачи для самостоятельного решения.
1.
определить координаты центра и найти радиус каждой из следующих
сфер
а)
2 2 2
12 4 6 0
x y z x y z
+ + − + − =
;
б)
2 2 2
8 0
x y z x
+ + + =
;
в)
2 2 2
6 7 0
x y z z
+ + − − =
;
г)
2 2 2
2 4 6 22 0
x y z x y z
+ + − + − − =
.
2.
Составить уравнение сферы в каждом из следующих случаев:
а) сфера имеет центр
( 3;2;5)
O
−
и радиус
5
r
=
;
б) сфера имеет центр
(0;0;0)
O
и радиус
2
r
=
;
в) сфера проходит через точку
( 2;5;3)
A
−
и имеет центр
(4; 2;3)
O
−
;
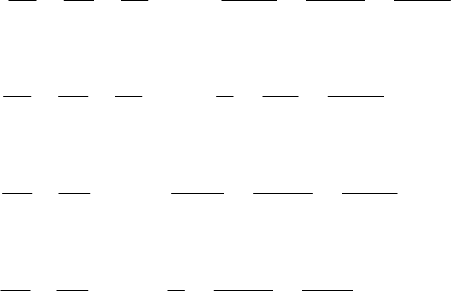
70
г) точки
(3;4; 6)
A
−
и
(5; 6;4)
B
−
являются концами одного из диаметров
сферы;
д) центром сферы является начало координат и плоскость
16 15 12 75 0
x y z
− − + =
является касательной к сфере;
е) сфера имеет радиус
3
r
=
и касается плоскости
2 2 3 0
x y z
+ + + =
в
точке
(1;1; 3)
A
−
.
3.
Установить как расположена точка
(2; 1;3)
A
−
относительно каждой из
следующих сфер – внутри, вне или на поверхности:
а)
2 2 2
( 3) ( 1) ( 1) 4
x y z
− + + + − =
;
б)
2 2 2
3 2 3 0
x y z x y z
+ + − + − − =
;
в)
2 2 2
( 6) ( 1) ( 2) 25
x y z
− + − + − =
.
4.
Привести уравнение поверхности к каноническому виду, определить
вид и расположение поверхности, пользуясь переносом системы коор-
динат. Сделать чертеж.
а)
2 2 2
4 9 6 8 36 0
x y z x y z
+ + − + − =
;
б) 04412324
222
=
+
−
+
−
−
zxzyx ;
в) 01412101833
222
=
+
+
+
−
+
−
zyxzyx ;
г) 011306566
22
=
−
+
+
+
+
zyxzy .
5.
Найти точки пересечения поверхности и прямой:
а)
1
9
36
81
222
=++
zyx
и
4
2
6
4
3
3
+
=
−
−
=
−
zyx
;
б)
1
4
9
16
222
=−+
zyx
и
4
2
3
4
+
=
−
=
zyx
;
в)
z
yx
=+
3
5
22
и
2
3
1
2
2
1
−
+
=
−
−
=
+
zyx
;
г)
z
yx
=−
4
9
22
и
2
1
2
2
3
+
=
−
−
=
zyx
.
6.
Найти линии пересечения поверхностей второго порядка и координат-
ных плоскостей. Определить вид линии и поверхности. Сделать чер-
теж.
