Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.

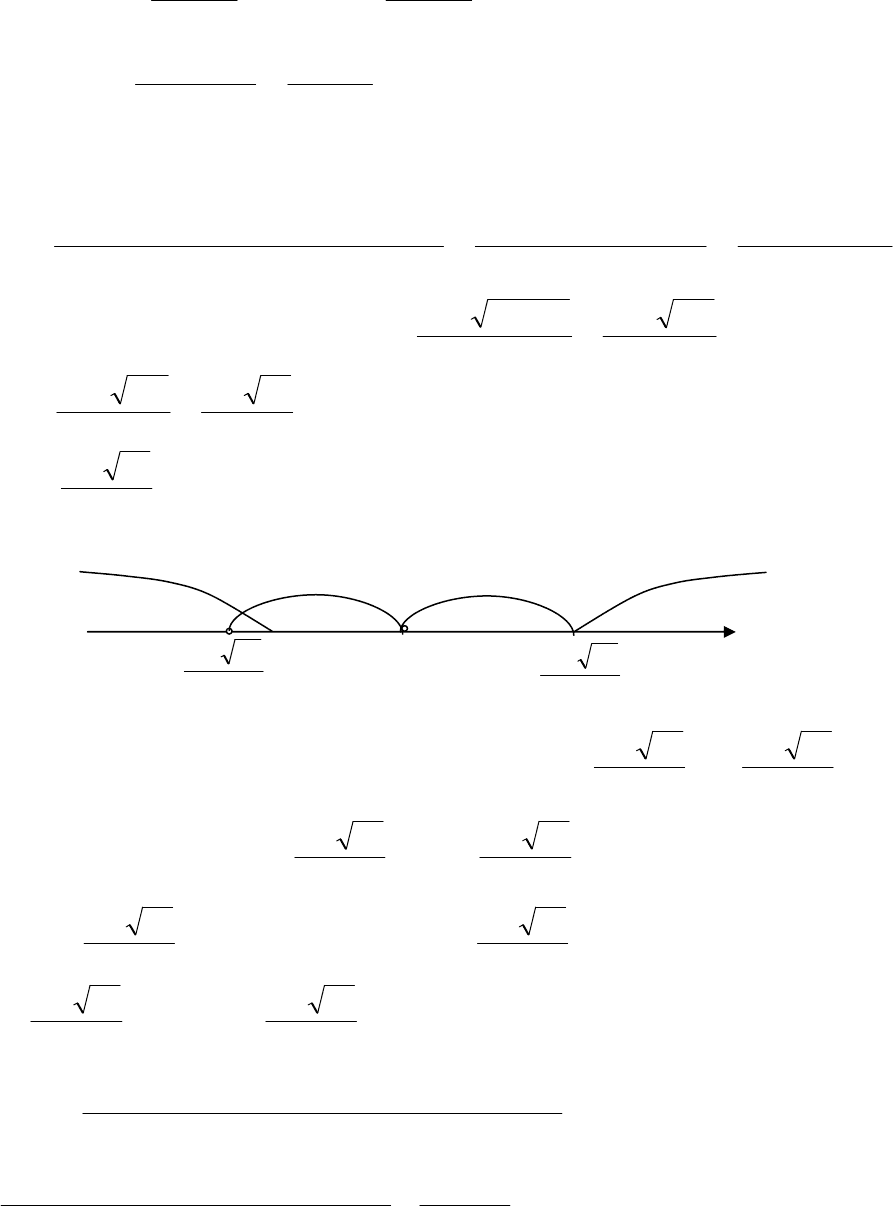
101
Имеем +∞=
−
+
+
→
3
14
lim
2
3
x
x
x
; −∞=
−
+
−
→
3
14
lim
2
3
x
x
x
.
3.
)(
3
14
3)(
1)(4
)(
22
xf
x
x
x
x
xf ≠
−−
+
=
−−
+−
=− ;
)
(
)
(
x
f
x
f
≠
−
⇒
функция общего
вида, непериодичная.
4.
(
)
2
2
2
2
2
22
)3(
1244
)3(
)14()3(8
)3(
)3)(14()3(14
−
−−
=
−
+−−
=
−
′
−+−−
′
+
=
′
x
xx
x
xxx
x
xxxx
y .
4
14812
4
414412
012440
2,1
2
±
=
+±
=⇒=−−⇒=
′
xxxy .
035,6
2
376
4
14812
1
≈
+
=
+
=x
035,0
2
376
2
−≈
−
=x .
Исследуем знак y
′
методом интервалов:
Функция возрастает на интервалах
−
∞−
2
376
; ;
+∞
+
;
2
376
,
убывает на интервалах
−
3;
2
376
;
+
2
376
;3 .
5.
2
376
1
+
=x - точка минимума,
2
376
2
−
=x - точка максимума.
5,48
2
376
≈
+
y ;
331,0
2
376
−≈
−
y .
6.
=
−
−−−−−−
=
′′
4
22
)3(
)1244)(3(2)3)(248(
x
xxxxx
y .
33
2
)3(
74
)3(
)1244(2)3)(248(
−
=
−
−−−−−
xx
xxxx
Исследуем знак y
′
′
.
+
+
_
_
2
376 −
2
376 +
3
x
+
:y
′
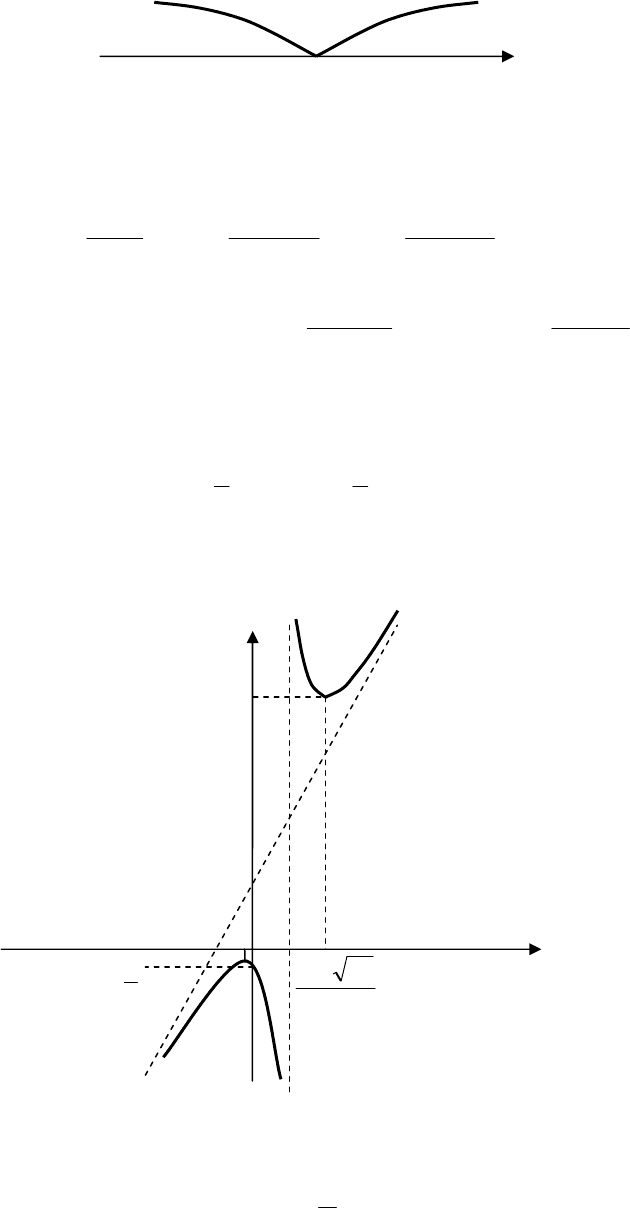
102
Функция выпукла на
интервале
)3;(
−∞
, вогнута на
интервале
);3(
+∞
7. Точек перегиба нет.
8. Находим наклонную асимптоту
b
kx
y
+
=
:
4
3
14
lim
)3(
14
lim
)(
lim
2
22
=
−
+
=
−
+
==
→∞→∞→∞
x
x
x
xx
x
x
xf
k
xxx
[ ]
12
3
112
lim4
3
14
lim)(lim
2
=
−
+
=
−
−
+
=−=
∞→∞→∞→
x
x
x
x
x
kxxfb
xxx
12
4
+
=
x
y
- наклонная асимптота.
9. Точки пересечения с осями координат:
Если
−⇒−=⇒=
3
1
;0
3
1
0
Myx
- точка пересечения с осью
y
0
.
Если ⇒=+⇒= 0140
2
xy
точек пересечения с осью
x
0
нет.
Строим график функции:
Пример 3.
Написать уравнение
касательной и нормальной прямых к
линии
xy 2sin
=
в точке
6
0
π
=x
.
Уравнение касательной прямой к графику
)(xfy
=
в точке
0
xx =
имеет вид:
))(()(
000
xxxfxfy −
′
=−
.
Уравнение нормальной прямой в той же точке имеет вид:
3
_
+
х
0
-3
3
2
376 +
3
1
−
х
y
48,7
12
124
+
=
xy
x=3
y”:
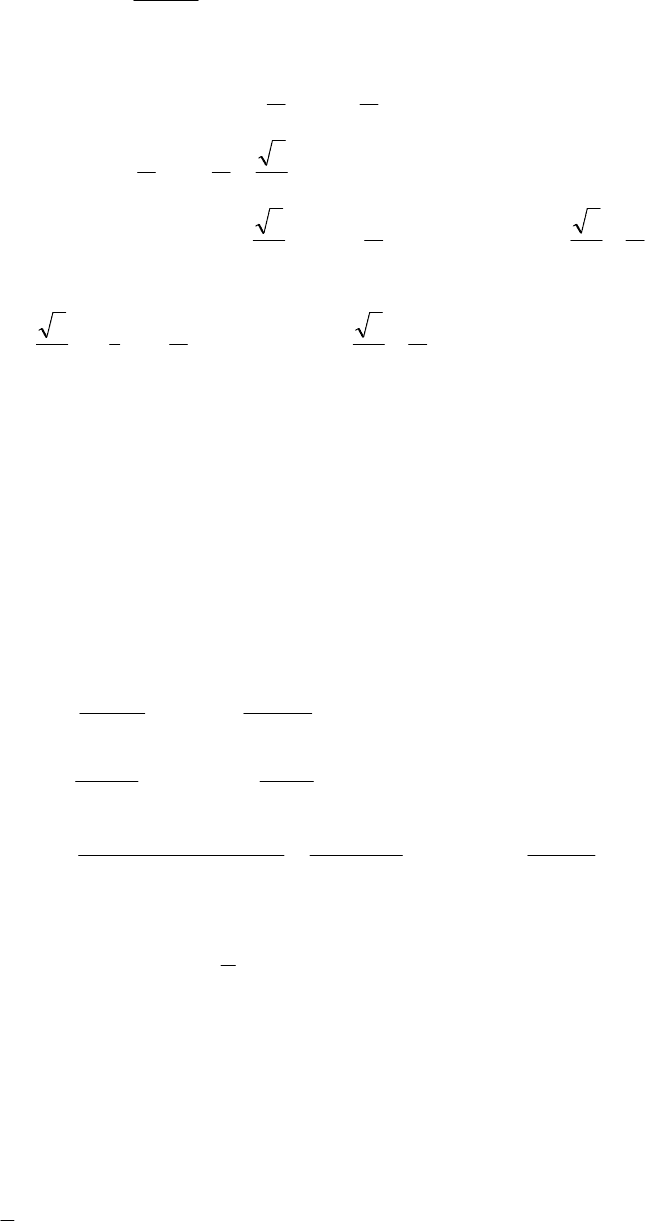
103
)(
)(
1
)(
0
0
0
xx
xf
xfy −
′
−=−
.
Для функции
xy 2sin
=
получаем:
xxf 2cos2)(
=
′
.
Отсюда
1
3
cos2
6
2cos2)(
0
==⋅=
′
π
π
xf
.
2
3
3
sin
6
2sin)(
0
==⋅=
ππ
xf
.
Теперь имеем:
−=−
6
1
2
3
π
xy
или
6
2
3
π
−+= xy
- уравнение
касательной прямой,
−−=−
61
1
2
3
π
xy
или
6
2
3
π
++−= xy
- уравнение нормальной прямой.
Пример 4.
Используя понятие дифференциала функции вычислить
приближенно
2,0−
e
.
Имеем формулу
))(()()(
000
xxxfxfxf −
′
+≈
в качестве
)(xf
берем
x
ey =
, а в качестве
0
x
xx
eexf =
′
=
′
)()(
, поэтому получаем:
8,02,01)2,0(
002,0
=−=−+≈
−
eee
Пример 5.
Используя формулу Тейлора, найти разложение функции
(
)
2
2ln xy −=
в окрестности точки
1
0
=x
, удерживая при этом три члена.
Имеем
( ) ( )
(
)
01ln12ln)(...
!2
)(
!1
)(
)()(
2
0
2
0
0
0
0
0
==−=+−
′
′
+−
′
+= xfxx
xf
xx
xf
xfxf
2
12
12
)(
2
2
)(
0
2
−=
−
⋅
−
=
′
⇒
−
−
=
′
xf
x
x
xf
(
)
(
)
(
)
6
1
24
)(
2
24
2
)2(222
)(
2
0
2
2
2
2
2
2
−=
−−
=
′′
⇒
−
−−
=
−
−+−−
=
′′
xf
x
x
x
xxx
xf
Окончательно получаем:
(
)
...)1(
2
6
)1(22ln
22
+−−−−=− xxx
или
(
)
...3412ln
22
+−+−=− xxx
Задачи для самостоятельного решения
.
1. Указать промежутки возрастания и убывания функций и найти их
экстремумы:
1.
xxx 3
3
1
y
23
−+=
2.
xx 3y
3
−=
3.
xxx ++=
23
2y
4.
xx 6y
2
+=
5.
132y
2
++= xx
6.
245y
2
+−= xx
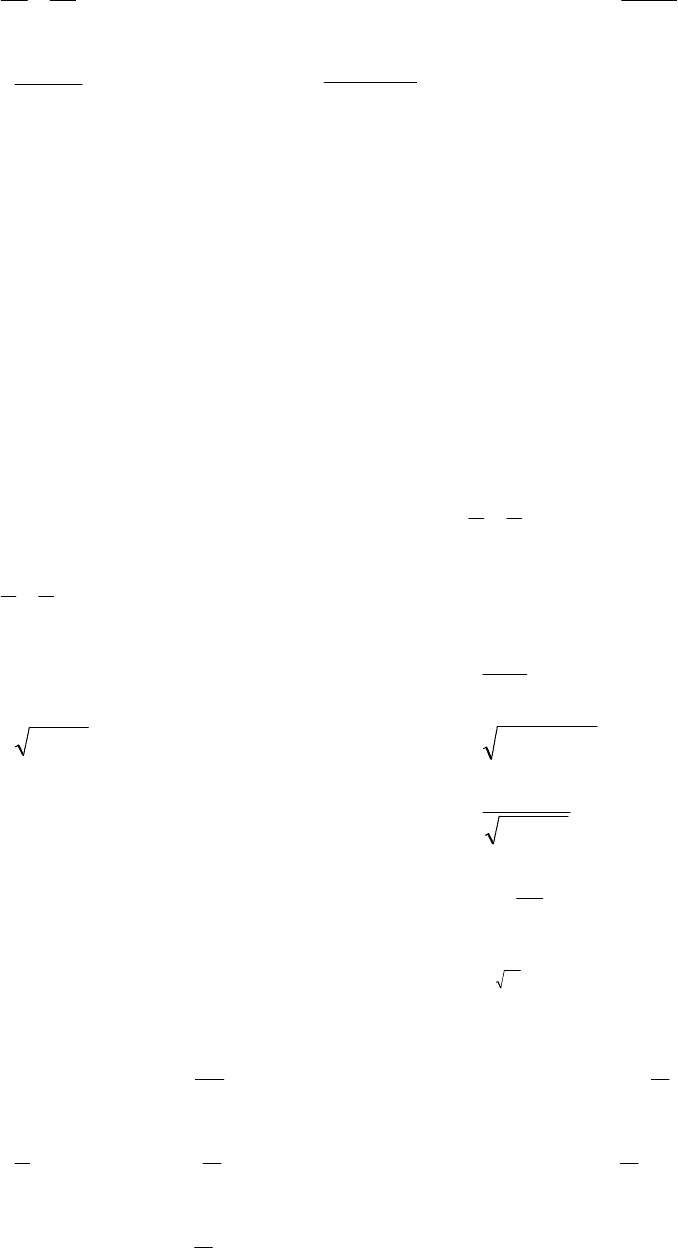
104
7.
2
34
3
4
y x
xx
−+=
8.
234
524y xxx −+=
9.
2
1
y
2
+
+
=
x
x
10.
1
12
y
2
−
−
=
x
x
11.
2
2
)5(
6
y
−
−+
=
x
xx
12.
)21ln(y xx
−
+
=
13.
x
xe
−
=y
14.
x
ex
−
=
2
y
15.
xx
ee
2
y
−−
−=
16.
)21ln(y
2
x+=
17.
x
ex
3
y =
2. Найти наименьшее и наибольшее значение функций в заданных
промежутках:
1.
[
]
2;1 ;4y
2
−+−= xx
2.
[
]
2;2 ;163y
2
−−+−= xx
3.
[
]
3;2 ;233y
23
−++−= xxx
4.
[
]
1;2 ;143y
34
−++= xx
5.
[
]
1;1 ;2y
35
−++−= xxx
6.
[ ]
1;5 ;
4
4
y −−+=
x
x
7.
[ ]
6;1 ;
2
8
y
x
x
+=
8.
[
]
5,1 ;3 ;23y
3
−+−= xx
9.
[
]
2;2 ;38y
24
−+−= xx
10.
[ ]
4;0 ;
1
1
y
+
−
=
x
x
11.
[
]
2;2 ;4y
2
−−= x
12.
[
]
3;1 ;)2(y
3
22
xx −=
13.
[
]
exx ;1 ;lny
2
=
14.
[ ]
3;3 ;
16
4
y
2
−
+
=
x
15.
[
]
exx ;1 ;ln2y
2
−−=
16.
[ ]
3;1 ;
8
y
4
x
x +=
17.
[
]
0;1 ;2)5(y −−=
−
x
x
18.
[
]
1;8 ;2y
3
2
−−=
x
19.
+=
2
3
;0 ;2sinsin2y
π
xx
20.
+=
4
;0 ;sincosy
2
π
xx
21.
+=
2
;0 ;sin2cos
2
1
y
π
xx
22.
+=
2
;0 ;cosy
2
π
xx
23.
+=
2
;0 ;cossiny
44
π
xx
105
3. Решить задачи, используя элементы дифференциального
исчисления.
1. Число 20 разбить на такие 2 слагаемых, чтобы сумма их квадратов
была наименьшей.
2. Число 180 разбить на 3 положительных слагаемых так, чтобы 2 из
них относились как 1:2, а произведение 3 слагаемых было наибольшим.
3. Найти число, которое превышало бы свой квадрат на
максимальное значение.
4. Требуется оградить забором прямоугольный участок земли
площадью 294 м
2
и затем разделить этот участок забором на 2 равные
части. При каких линейных размерах участка длина всего забора будет
наименьшей.
5. Определить размеры открытого бассейна с квадратным дном
объемом 32 м
3
так, что на облицовку его стен и дна пошло наименьшее
количество материала.
6. Консервная банка данного объема имеет форму цилиндра. Каково
должно быть соотношение ее размеров (высоты и диаметра), чтобы на
изготовление пошло минимальное количество жести.
7. Каково должно быть отношение высоты к радиусу основания
конического шатра данной вместимости, чтобы на его изготовление пошло
наименьшее количество материи.
8. Найти длины сторон прямоугольника наибольшей площади,
вписанный в прямоугольный треугольник со сторонами 18, 24, 30 см и
имеющего с ним общий прямой угол.
4. Указать участки выпуклости и вогнутости функций и найти точки
перегиба:
1.
13y
23
+++= xxx
2.
564y
23
++−= xxx
3.
732y
23
++= xx
4.
xxx +−=
23
23y
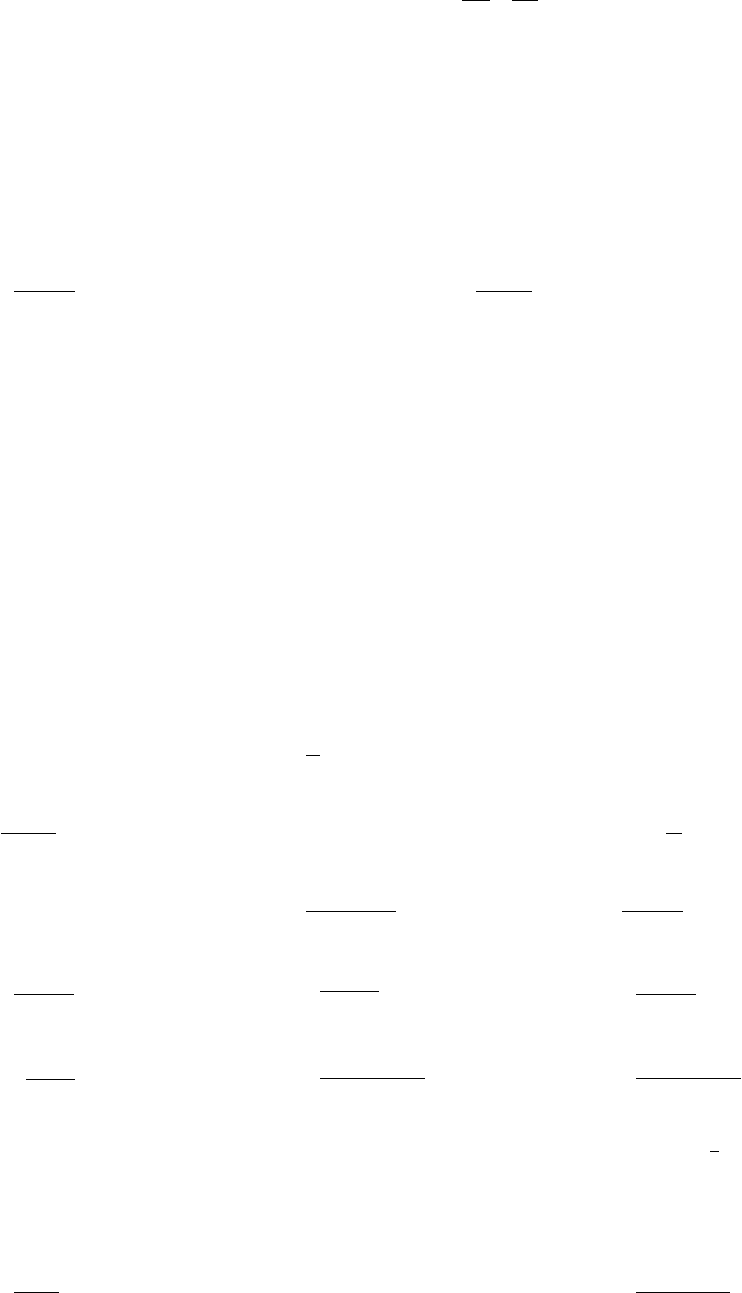
106
5.
234
3y xxx −−=
6.
2
34
6
12
y x
xx
−+=
7.
234
352y xxx +−=
8.
x
xe=y
9.
x
xe
2
y
−
=
10.
x
ex
22
y
−
=
11.
2
y
x
xe
−
=
12.
)1ln(y
2
x+=
13.
)24ln(y
2
x+=
14.
)47ln(y
2
x+=
15.
4
y
2
+
=
x
x
16.
1
1
y
2
+
=
x
5. Для нижеприведенных функций: а) найти область определения,
интервалы непрерывности, точки разрыва; б) определить четность
(нечетность), периодичность функций; в) найти асимптоты (вертикальные,
наклонные, горизонтальные) графика; г) найти интервалы монотонности и
точки экстремума; д) найти интервалы выпуклости и вогнутости графика;
е) найти точки пересечения графика с осями координат; ж) построить
графики:
1.
xxx 65,4y
23
+−=
2.
2
)4)(2(
8
1
y −+= xx
3.
35
53y xx −=
4.
2
1
4
y
x
+
=
5.
16425,0y
23
+−−= xxx
6.
43
4
1
y xx +=
7.
)4(5,0y
22
−= xx
8.
1
2
y
2
++
=
x
x
9.
4
8
y
2
+
=
x
x
10.
1
4
y
2
2
+
−
=
x
x
11.
2
53
y
+
+
=
x
x
12.
4
y
2
2
−
=
x
x
13.
2
2
2
y
−
+
=
x
x
14.
2
3
2
y
2
+−
=
x
x
15.
3
4
y
2
+−
=
x
x
x
16.
2
y
x
e
−
=
17.
x
ex
2
)2(y
−
+=
18.
2
)4(y
x
ex−=
19.
)1ln(y
2
x+=
20.
2
y
x
xe
−
=
21.
xxlny
=
22.
1
y
+
=
x
e
x
23.
xx
−
+= 22y
24.
2
6
y
2
−
−−
=
x
xx

107
25.
2
2
5y x
x
−−=
26.
1
2
3
2
3
y −
−
−
+
=
x
x
27.
3
4
)1(
y
+
=
x
x
28.
3
3
3y xx −=
29.
3
2
2y xx −=
30.
32
)3()1(y −⋅−= xx
6. Составить уравнение касательной и нормальной прямых к кривой
)(y xf
=
в точке x=
х
о
1.
2 ;325y
o
23
=+−+= xxxx
2.
0 ;
2
y
o
=
+
= x
x
x
3.
1 ;
3
1
y
o
2
2
=
++
+
= x
x
x
x
4.
0 );31ln(y
o
=+= xx
5.
8
;2siny
o
π
== xx
6.
0 ;)1(y
o
2
=+=
−
xex
x
7.
0 );12ln(y
o
=−= xe
x
8.
6
;cosy
o
2
π
== xx
9.
π
==
o
sin
;y xe
x
10.
1 ;
2
y
o
2
=−= x
x
x
11. На параболе
2
xy =
взяты две точки с абсциссами .3;1
21
== xx .
Через эти точки проведена секущая. Написать уравнение касательной к
данной кривой, которая параллельна проведенной секущей.
12.Касательная к кривой
2
3 xxy −=
перпендикулярно прямой,
проходящей через точки (2;0) и (0;1). Составить уравнение этой
касательной.
13. Составить уравнение касательных к кривой
1
3
+= xy
,
параллельных прямой
013
=
+
−
xy
.
14. Составить уравнение касательной к кривой
)1ln(
−
=
xy
перпендикулярно прямой, образующей с осью ОХ угол в 135
о
.
15. Составить уравнение касательной к кривой
3
72
y
−
−
=
x
x
,
проходящей: а) через начало координат; б) параллельно прямой
024
=
−
−
yx
; в) перпендикулярно прямой
0522
=
−
+
yx

108
16. Составить уравнение касательной к кривой
x
e
−
=y
, проходящей:
а) параллельно биссектрисе второго и четвертого координатных углов; б)
проходящей через точку (-1;0).
7. Используя понятие дифференциала вычислить приближенно:
1.
17
2.
26
3.
37
4.
3
28
5.
3
65
6.
7
126
7.
4
82
8.
4
260
9.
4
627
10.
5
33
11.
3
245
12.
o
32sin
13.
o
47sin
14.
o
62 cos
15.
o
48 cos
16.
o
46 tg
17.
o
26 tg
18.
o
33 ctg
19.
o
94 ctg
20.
2,0
e
21.
1,0
−
e
22.
3,0
e
23.
1,1ln
24. ln 1,2 25. ln 0,9
26. ln 0,8 27.arctg 1,05
28. arcctg
0,96
8. Используя формулу Тейлора, найти разложение заданных функций
в окрестности точки
х=х
о
удерживая при этом n членов:
1.
3 ;1 ;12y
o
23
==−+= nxxx
2.
3 ;2 ;43y
o
23
==+−= nxxxx
3.
4 ;1 ;22y
o
24
==++−= nxxxx
4.
5 ;1 ;3y
o
25
==+−= nxxxx
5.
4 ;1 ;23y
o
24
=−=++−= nxxxx
6.
3 ;2 ;142y
o
23
=−=+++= nxxxx
7.
3 ;0 ;y
o
2
===
−
nxe
x
8.
2 ;0 ;siny
o
2
=== nxx
9.
2 ;0 );21ln(y
o
2
==+= nxx
10.
2 ;0 ;1y
o
4
==+= nxx
11.
2 ;1 ;31y
o
==+= nxx
12.
2 ;1 ;arctgy
o
=== nxx
13.
2 ;0 ;arcsiny
o
=== nxx
14. 2 ;1 ;71y
o
3
==+= nxx
15.
2 ;1 ;115y
o
4
==+= nxx
16.
2 ;1 );2ln(y
o
3
==+= nxxx
17.
3 ;0 );cos(y
o
2
=== nxx
4.4. Неопределенный интеграл.
Таблица интегралов
(C - произвольная постоянная).
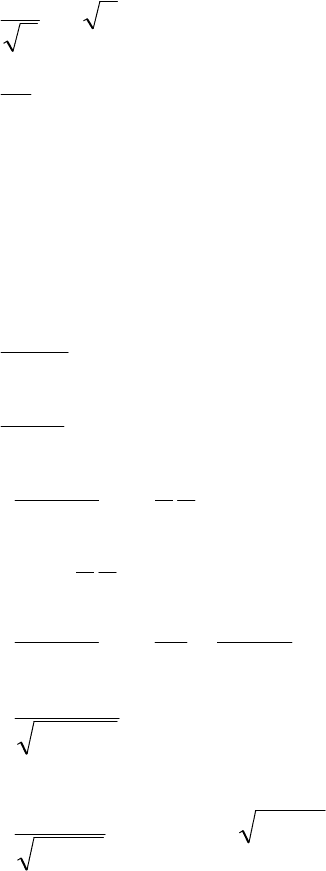
109
1. .= 1, ,1)/(=
1
constCxdxx
ααα
αα
−≠++
+
∫
2.
.2=
Cx
x
dx
+
∫
3.
.||ln=
Cx
x
dx
+
∫
4. 8.2.71828182 ,= ≈+
∫
eCedxe
xx
5. 0.> 1, ,= ,ln/=
aaconstaCaadxa
xx
≠+
∫
6. .cos=sin
Cxdxx
+−
∫
7. .sin=cos
Cxdxx
+
∫
8.
.=
cos
1
2
Cxdx
x
+
∫
9.
.=
sin
1
2
Cxdx
x
+−
∫
10.
=
1
=
1
22
C
a
x
a
dx
a
x
+
+
∫
0.> ,= ,
1
=
1
aconstaC
a
x
a
+−
11.
0.> ,= ,
||
||
ln
2
1
=
1
22
aconstaC
ax
ax
a
dx
ax
+
+
−
−
∫
12.
=)/(arcsin=
1
22
Caxdx
xa
+
−
∫
0.> ,= ,)/(arccos=
1
aconstaCax
+
−
13.
.= ,||ln=
1
2
2
constbCbxxdx
bx
+++
+
∫
Основные
свойства неопределенного интеграла
(C=const).
1. .)()(=))()((
dxxvdxxudxxvxu
∫∫∫
±±
2. .)(=)(
dxxuCdxxCu
∫∫
3. .)(=))((
Cxfxfd
+
∫
4.
(
)
).(=)( xudxxu
'
∫
5.
(
)
.)(=)( dxxudxxud
∫
Интегрирование по частям: .= duvuvdvu
∫∫
−
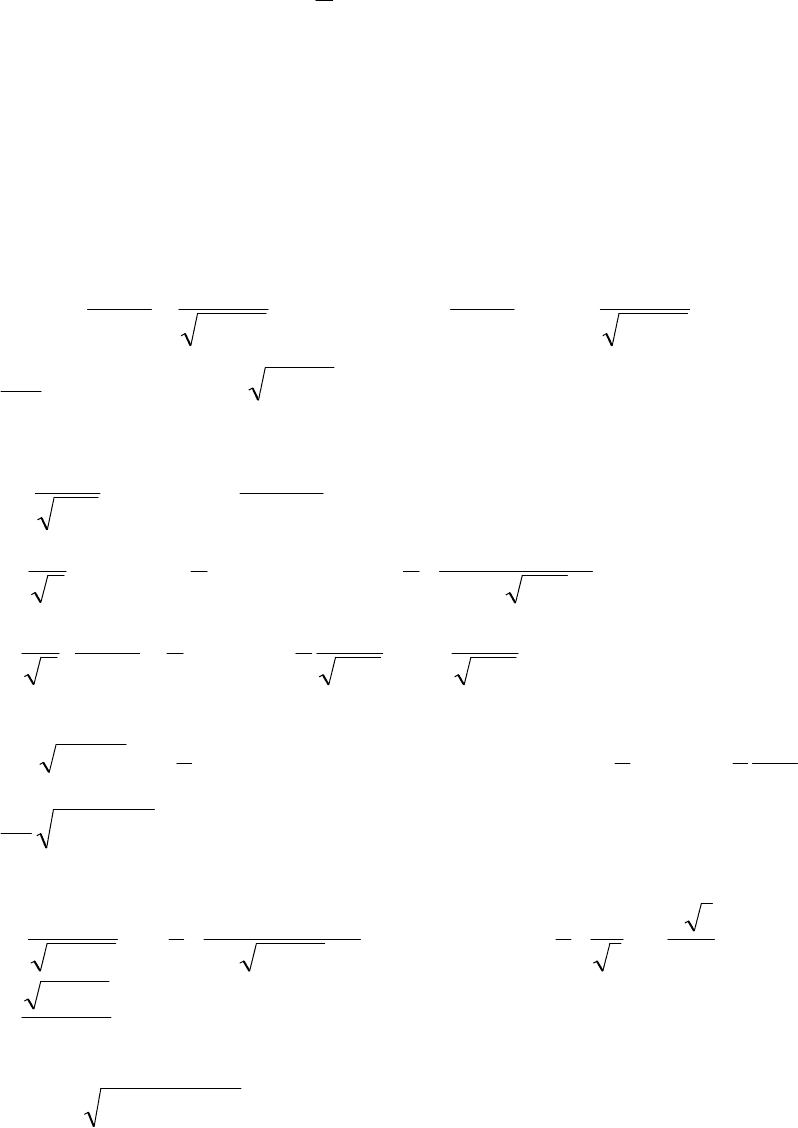
110
Замена переменной: =)( dxxu
∫
=
′
=
=
−
)(
)(
)(
1
xt
dttdx
tx
ϕ
ϕ
ϕ
.)())((= dtttu
'
ϕϕ
∫
При нахождении интеграла часто помогают две формулы: формула
изменения функции, стоящей под знаком дифференциала:
],)([
1
=)]([ mkxfd
k
xfd +⋅
const
m
k
=
,
;
и формула внесения под знак дифференциала:
(
)
)).(()(=)(=)(=)()( xFdxgxFdxxfdxxgxf
∫∫∫
⋅
Приведем
примеры
решения задач по нахождению неопределенных
интегралов.
В примерах 1-6 применяются свойства интегралов и описанные выше
две формулы.
1
. dx
x
x
x
)
8
3
sin
5
(8
2
2
−
−+
∫
= dx
x
dx
x
dx
x
8
1
3
sin
1
58
2
2
−
−+
∫∫∫
=
=
Cxxctgx
x
+−+−− |8|ln35
8
ln
8
2
.
2
. dx
x
x
x
)
23
7
2cos9
2
5
(
2
5
8
+
−−
−
∫
=
=
dx
x
xxddxx
22
5/8
5
)3/2(
1
3
7
)2(2cos
2
9
2
5
+
−⋅−−
∫∫∫
−
=
=
C
x
arctgx
x
+−−
−
⋅−
−
3/23/2
1
3
7
)2sin(
2
9
5/3
2
5
5/3
5
.
3
. dxx
7
43 +
∫
= )43()43(
3
1
7/1
+⋅+
∫
xdx =[
4
3
+
=
x
t
]= dtt
∫
7/1
3
1
=
C
t
+
7
/
8
3
1
7/8
=
=
Cx ++
7
8
)63(
24
7
.
4.
∫
− x
dx
83
=
∫
−
+
−
⋅
−
x
xd
83
)3)8((
8
1
=[
x
t
8
3
−
=
]=
∫
−
t
dt
8
1
=
C
t
+−
8
2
=
=
C
x
+
−
−
4
83
.
5.
dxxx
7
2
1)sin(6cos +
∫
=
(
)
∫
= xxdx sincos
= xdx sin1)sin(6
7/2
+
∫
=
