Медведев А.В. и др. Математический практикум. І курс: Учебное пособие
Подождите немного. Документ загружается.


131
Вычисление объёмов тел вращения.
1
.
Объём тела, полученного вращением вокруг оси Оx, криволинейной
трапеции
{
)(0 xfy
≤
≤
,
}
bxa
≤
≤
определяется формулой
( )
dxxfV
b
a
2
∫=
π
.
2.
Объём тела, полученного вращением вокруг оси Оy, криволинейной
трапеции
{
)(0
ygx
≤≤
,
}
dyc
≤
≤
определяется формулой
( )
dyyg
b
c
V
2
∫=
π
.
Пример 8.
Найти объём тела, образованного вращения плоской фигуры,
ограниченной линиями
0,0,0 ,4
2
≥==−= xyxõó
а) вокруг оси Ox,
б) вокруг оси Oy.
а) Найдем объем тела вращения вокруг оси Ox.
( )
( )
.
15
256
5
32
3
64
328164
42
2
0
2
2
0
ππππ
=
+−==+−∫=−∫= dxõõdxõV
б) Найдем объём тела вращения вокруг оси Oy.
Из уравнения
2
4 ху
−
=
находим
40 , 4 ≤≤−±=
yyx
. Используя
формулу для нахождения объема тела вращения, получаем
(
)
( )
.8816)4(4
4
0
2
4
0
ππππ
=−=−∫=−±∫= dyydyyV
Задачи для самостоятельного решения
.
Вычислить площади фигур, ограниченных графиками функций
1. .0,4
2
=−= yxxy
2. y x y= + =
2
1 2, .
3. y x y x x= + = = − =2 1 0 1 1
2
, , , .
4. y x y x= = +
2
2, .
5. y e y x x
x
= = = =, , , .0 2 0
6. x y x y= − = −( ) , .2 4 8
3
7.
y
x
y
x
=
=
=
arccos
,
,
.
0
0
8. y x y x y= − + = =2 0, , .
9. y x y x
=
=
=
sin , , .2 1 0
10. x y x y y= − = −4 2
2 2
, .
Вычислить площади фигур, ограниченных линиями, заданными
уравнениями:
11.
x t
y t
=
=
2
3
cos ,
sin .
12.
x t t
y t
= −
= −
sin ,
cos ,1
y
t
=
≤
≤
0
0
2
,
π
.
13.
x t
y t
=
=
cos ,
sin .
3
3
(астроида)
14.
x t
y t
=
=
3
8
cos ,
sin ,
y
y
=
≥
4
4
(
)
.
15.
x t t
y t t
= −
= −
2 2
2 2
cos cos ,
sin sin .
(кардиоида)

132
Вычислить площади фигур, ограниченных линиями, заданными
уравнениями в полярных координатах.
16.
r
=
cos
.
2
ϕ
17. r
=
sin .
ϕ
18. r
=
sin
ϕ
,
r
=
2sin
ϕ
.
19. r
=
sin .6
ϕ
20.
r
=
2
cos
ϕ
,
r
=
3
cos
ϕ
.
Вычислить длины дуг кривых, заданных уравнениями в прямоугольной
системе координат.
21. y
x x
= −
2
4
2
ln
,
1
2
≤
≤
x
.
22. y x
=
−
ln cos
,
0
6
≤ ≤x
π
.
23. y x= −( )1
3
2
,
1
2
≤
≤
x
.
24. y
e e
x x
=
+
+
−
2
3
,
0
2
≤
≤
x
.
25. y x= −ln( )
2
1
,
2
3
≤
≤
x
.
Вычислить длины дуг кривых, заданных параметрическими линиями.
26.
x t t
y t
= −
= −
sin ,
cos ,1
0
2
≤
≤
t
π
.
27.
x t
y t
=
=
10
10
3
3
cos ,
sin ,
0
2
≤ ≤t
π
.
28.
x t t t
y t t t
= −
= −
2
2
(cos sin ),
(sin cos ),
0
2
≤ ≤t
π
.
29.
x t
y t
t
=
= −
2
3
3
,
,
0 3≤ ≤
t
.
30.
x e t t
y e t t
t
t
= +
= −
(cos sin ),
(cos sin ),
0
≤
≤
t
π
.
Вычислить длины дуг кривых, заданных уравнениями в полярных
координатах.
31. r
=
−
1 sin
ϕ
,
− ≤ ≤ −
π
ϕ
π
2
6
.
32.
r
e
=
3
3
4
ϕ
,
− ≤ ≤
π
ϕ
π
2
2
.
33. r
=
2 sin
ϕ
,
0
6
≤ ≤
ϕ
π
.
34.
r
=
−
2
1
(
cos
)
ϕ
,
− ≤ ≤ −
π ϕ
π
2
.
35. r
=
+
6 1( sin )
ϕ
,
− ≤ ≤
π
ϕ
2
0
.
Вычислить объем тела, образованного вращением фигур, ограниченных
графиками функций вокруг указанной оси.
36. y x
2
=
,
x
=
1
, Ох.
37.
y x
=
3sin
,
y x
=
sin
,
0
≤
≤
x
π
,Ох.
38. y x=
3
,
y x=
2
, Оу.
39. y e
x
=
−
1
,
y
=
0
,
x
=
0
,
x
=
1
,Ох.
40. y x
2
2= −
,
y
=
0
,
y x=
3
,
y
=
1
,Оу
4.7 Несобственные интегралы.
1. Интегралы с бесконечными пределами.
Если функция
(
)
xfy
=
непрерывна при
,
+∞
<
≤
x
a
то по определению
( )
∫ ∫
+∞
+∞→
=
a
b
a
b
dxxfdxxf
)(lim
(1)

133
Если существует конечный предел в правой части формулы (1), то
несобственный интеграл называется сходящимся, если этот предел не
существует или равен
∞
, то – расходящимся.
Аналогично определяется интеграл
∫
∞−
b
dxxf )(
и интеграл
∫∫ ∫
+∞
∞−
−∞→+∞→
+=
c
a
b
c
ab
dxxfdxxfdxxf
)(lim)(lim)(
(2)
Имеют место следующие свойства.
1) Если
)(xF
- первообразная для
)(xf
и существует конечный предел
)()(lim +∞=
+∞→
FxF
x
, то интеграл (1) сходится и равен
∫
+∞
−+∞=
a
aFFdxxf
)()()(
Если же
)(lim xF
x
+∞→
не существует или равен
∞
, то интеграл (1) расходится.
2) Если при
+∞
<
≤
x
a
,
0)(,0)(
>
>
xgxf
и существует предел
0
)(
)(
lim ≠
+∞→
xg
xf
x
,
то интегралы
∫
+∞
a
dxxf
)(
и
dxxg
a
∫
+∞
)(
сходятся или расходятся одновременно.
3)
∫
+∞
−
a
p
x
dx
)(
α
сходится при
1
>
p
и расходится при
1
≤
p
(здесь
α
>
a
).
Пример 1.
Вычислить
dxxe
x
∫
+∞
−
0
2
.
Имеем
( )
2
1
1lim
2
1
2
1
limlim
2222
0
00
=−−=
−==
−
+∞→
−
+∞→
−
+∞→
+∞
−
∫∫
b
b
b
x
b
b
x
b
x
eedxxedxxe
.
Пример 2.
Исследовать на сходимость интеграл
∫
+∞
++
+
1
2
64
12
dx
xx
x
.
Имеем
2
6
4
2
lim
1
:
6
4
12
lim
2
2
2
=
++
+
=
++
+
+∞→+∞→
x
x
xx
x
x
x
x
xx
. Но так как
∫
+∞
1
x
dx
расходится
(
1
=
p
), то интеграл
∫
+∞
++
+
1
2
64
12
dx
xx
x
расходится.
2. Интегралы от неограниченных функций.
Если функция
)(xfy
=
непрерывна при
bxa
<
≤
и
∞
=
)(bf
, то по
определению
∫∫
−
→
=
ε
ε
b
a
b
a
dxxfdxxf
)(lim)(
0
(3)
Если существует конечный предел в правой части формулы (3), то
несобственный интеграл называется сходящимся, в противном случае –
расходящимся.
В случае, когда
),( bac
∈
и
∞
=
)(cf
:
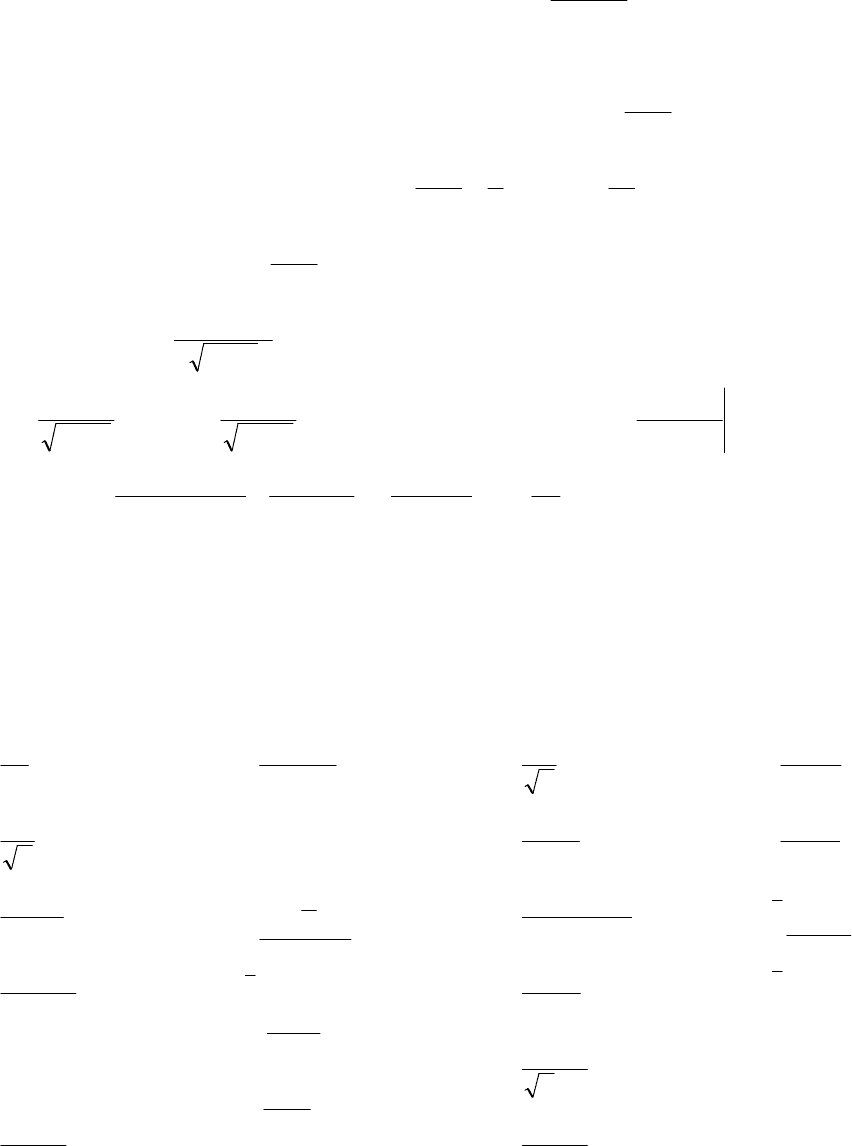
134
∫∫∫
+
→
−
→
++
+=
b
c
c
a
b
a
dxxfdxxfdxxf
δ
δ
ε
ε
)(lim)(lim)(
00
(4)
Эталоном для сравнения служит интеграл
∫
−
b
a
q
xb
dx
)(
, который сходится при
10
<
<
q
и расходится при
1
≥
q
.
Пример 1.
Исследовать на сходимость интеграл
∫
1
0
2
sin
dx
x
x
.
При
xxx ~sin0
→
. Поэтому
x
x
x 1
~
sin
2
. Но
∫
1
0
x
dx
расходится. Отсюда
заключаем, что интеграл
∫
1
0
2
sin
dx
x
x
расходится.
Пример 2.
∫
−
1
0
2
1
arcsin
x
xdx
.
∫∫∫
−
−
→→
−
→
===
−
=
−
ε
ε
εε
ε
ε
1
0
1
0
2
00
1
0
2
0
1
0
2
2
arcsin
lim)(arcsinarcsinlim
1
arcsin
lim
1
arcsin x
xxddx
x
x
dx
x
x
8
0
2
1arcsin
2
0arcsin
2
)1(arcsin
lim
2222
0
πε
ε
=−=
−
−
=
→
Задачи для самостоятельного решения
.
Установить сходимость или расходимость несобственных интегралов и в
случае сходимости вычислить их.
1.
dx
x
4
1
+∞
∫
.
2.
dx
x
1
+∞
∫
.
3.
dx
x
2
0
9+
+∞
∫
.
4.
xdx
x
2 9
2
0
+
+∞
∫
.
5. xe dx
x
−
+∞
∫
0
.
6.
dx
x x
ln
2
2
+∞
∫
.
7.
arctg x
x
dx
2
2
1
1+
+∞
∫
.
8. xe dx
x
−
+∞
∫
2
0
.
9.
cos( )
1
2
2
x
dx
x
π
+∞
∫
.
10.
dx
x x
ln
2
+∞
∫
.
11.
dx
x
−
∫
1
1
2
.
12.
dx
x
0
1
∫
.
13.
e dx
e
x
x
−
∫
1
0
4
.
14.
dx
x x
2
1
2
2 3+ −
∫
.
15.
x dx
x
2
3
1
2
1−
∫
.
16.
dx
x
−
∫
1
1
4
.
17.
dx
x x
e
ln
2
1
∫
.
18.
dx
x
8
3
2
3
−
∫
.
19.
x dx
x
3
4
1
2
1−
∫
.
20.
dx
tgx −
∫
1
4
3
π
π
.
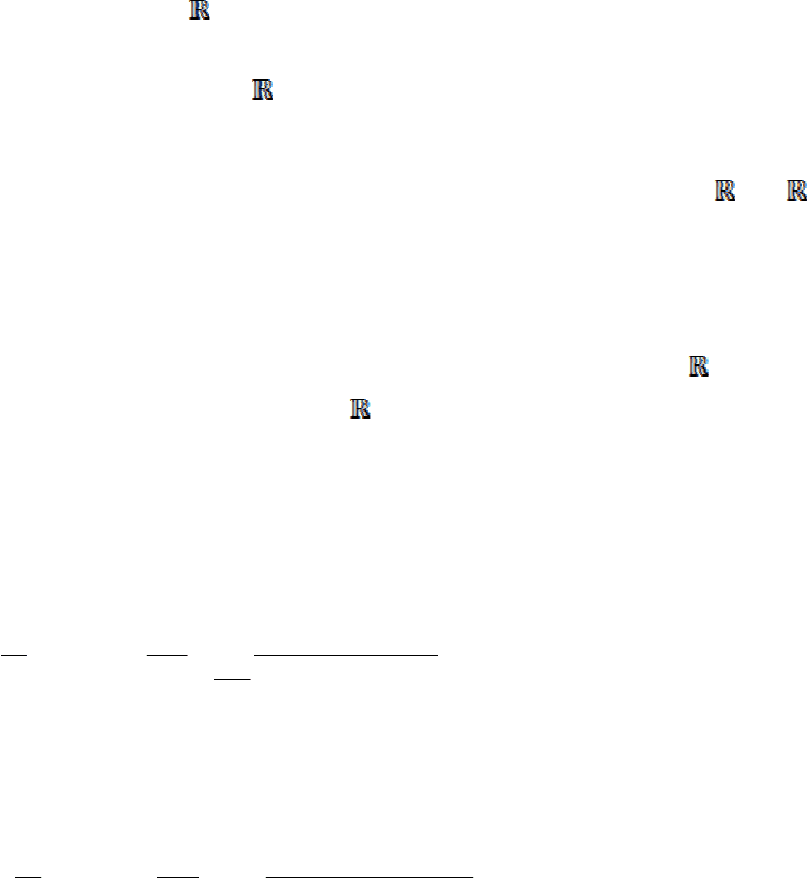
135
5. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Пусть имеются n переменных величин и каждому набору их значений
(х
1
,х
2
,… ,х
n
) из некоторого множества X соответствует вполне определенное
значение переменной z
∈
, тогда говорят, что задана функция нескольких
переменных z = f(х
1
,х
2
, х
3
… х
n
), где х
1
,х
2
,…, х
n
– независимые переменные, Х –
область определения функции,
– множество значений функции, z – зависимая
переменная, f – закон, соответствие.
Рассмотрим множество G, состоящее из пар вида (x;y), где х
∈
, y
∈
, с
геометрической точки зрения множество G, это подмножество точек коорди-
натной плоскости оху
Функцией двух переменных на множестве G называется закон, по которому
любому элементу (x;y)
∈
G соответствует единственный элемент z
∈
: z = f(x;y),
где G – область определения функции,
– множество значений функции, х, у –
независимые переменные (или аргументы), z – зависимая переменная.
Частной производной от функции двух переменных z = f(x;y)по независи-
мой переменной х называется конечный предел, вычисленный при постоянном
значении у:
(
)
(
)
.
;
limlim
00
'
x
yxfxxf
x
z
z
x
z
x
x
x
x
∆
−∆+
=
∆
∆
==
∂
∂
→∆→∆
Частной производной от функции двух переменных z = f(x;y)по независи-
мой переменной у называется конечный предел, вычисленный при постоянном
значении х:
(
)
(
)
.
;;
limlim
00
y
yxfyyxf
y
z
z
y
z
y
y
y
y
∆
−∆+
=
∆
∆
=
′
=
∂
∂
→∆→∆
Для вычисления частных производных можно применить обычные прави-
ла и формулы дифференцирования функции одной переменной.
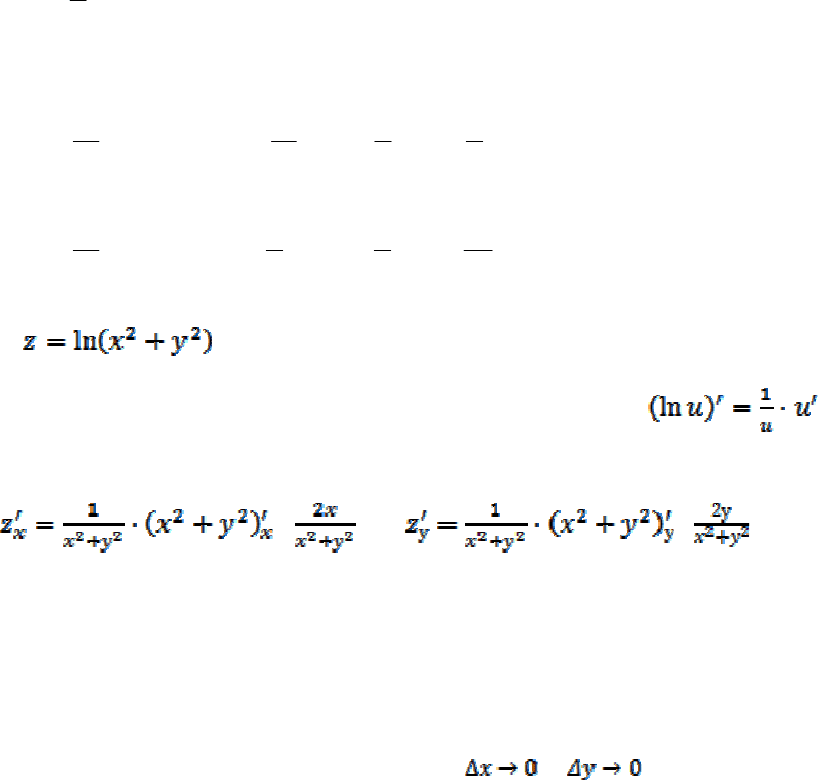
136
Пример 1. Найти частные производные функций:
1. z =
y
x
. Используя правило дифференцирования: постоянный множитель
можно выносить за знак производной, получим
x
z
∂
∂
=
{
}
consty
=
=
х
y
x
′
=
x
y
′
⋅
1
x
=
y
1
,
{ }
′
===
∂
∂
y
x
constx
y
z
y
= x
′
⋅
y
1
y
= -
2
y
x
.
2.
.
Применяя формулу производной сложной функции
, полу-
чим:
= , = .
Функция z = f(x;y) называется дифференцируемой в точке М(x;y), если ее
полное приращение в этой точке может быть представлено в виде:
(
)
(
)
yyxxyxyzxzz
yx
∆⋅∆∆+∆⋅∆∆+∆⋅
′
+∆⋅
′
=∆ ;;
βα
, (*)
где
α
и
β
бесконечно малые функции при и .
Полным дифференциалом dz дифференцируемой в т. М(х;y) функции
z = f(x;y)называется линейная относительно
x
∆
и
y
∆
часть полного приращения
этой функции, т. е.
.
yzxzdz
yx
∆⋅
′
+∆⋅
′
=
Как и для функции одной переменной можно доказать, что приращение ар-
гументов равно их дифференциалам
(
)
dyydxx
=
∆
=
∆
;
, тогда:
.
dyzdxzdz
yx
⋅
′
+⋅
′
=
Применение полного дифференциала к приближенным вычислениям
Из формулы (*) видно, что
dzz
≈
∆
, т. е.
ƒ
(
)
yyxx
∆
+
∆
+
;
−ƒ
(
)
,;
dyzdxzyx
yx
′
+
′
≈

137
или ƒ
(
)
≈
∆
+
∆
+
yyxx
;
ƒ
(
)
.;
yzxzyx
yx
∆
′
+∆
′
+
(**)
Пример 2. Вычислить
.96,302,3
22
+
Рассмотрим функцию
22
yxz +=
, фиксируем x=3; y = 4; примем
;02,0
=
∆
x
.04,0
−
=
∆
y
Найдем значение функции в точке (3;4):
z (3;4) = ƒ(3;4)=
543
22
=+
.
Вычислим частные производные функции и их значения в точке (3;4).
2222
2
2
1
yx
x
x
yx
z
x
+
=⋅
+
=
′
,
.2
2
1
2222
yx
y
y
yx
z
y
+
=⋅
+
=
′
5
3
)4;3( =
′
x
z
,
.
5
4
)4;3( =
′
y
z
Подставляя полученные значения в формулу (**), получим
( ) ( )
98,404,0
5
4
02,0
5
3
596,302,3
22
≈⋅+⋅+≈+
.
Дифференцирование сложной и неявной функций. Пусть z = f(x; y)
функция двух переменных x и y, каждая из которых в свою очередь является
функцией независимой переменной t, т.е. x =
ϕ(
t
),
y=
ψ(
t
)
, тогда функция
z=
ƒ(ϕ(
t
);
ψ(
t
))
является сложной функцией независимой переменной t.
Производная функции вычисляется по следующей формуле:
dt
dy
y
z
dt
dx
x
z
dt
dz
⋅
∂
∂
+⋅
∂
∂
=
Пусть x и y - аргументы функции двух переменных, т.е. z = f(x; y), а
x =
ϕ(
u
;
v
)
, y =
ψ(
u
;
v
)
, тогда сложная функция z =
ƒ(ϕ(
u
;
v
);ψ(
u
;
v
))
также
имеет частные производные:
uy
z
ux
z
u
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
ψ
ϕ
,
vy
z
v
u
x
z
v
z
∂
∂
⋅
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
∂
ψ
.
Структура этих формул сохраняется и при большем числе переменных.
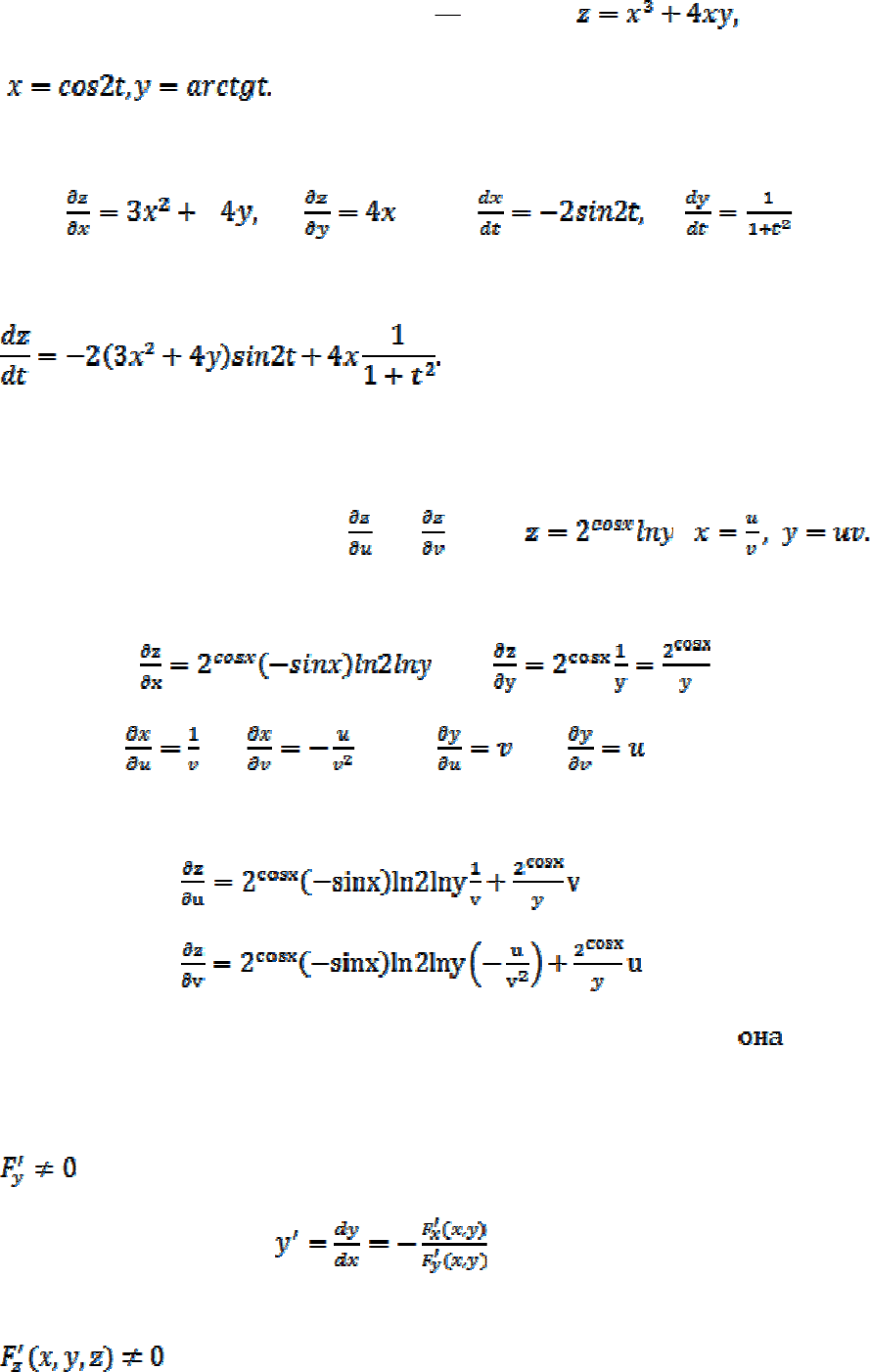
138
Пример 3. Найти производную
dt
dz
функции если
Согласно формулам находим:
, .
Ответ запишем в виде:
Переменные x и y можно как сохранить в ответе, так и выразить их через t, в
зависимости от того, что проще.
Пример 4. Определить
и , если ,
Находим частные производные
, ,
, , , .
Составляем суммы соответствующих произведений:
,
.
Функция y=y(x) называется неявной функцией, если
определяется
уравнением F(x,y)=0, неразрешимым относительно у.
Если уравнение F(x,y)=0 задает некоторую функцию y(x) в неявном виде и
, то
.
Если F(x,y,z)=0 задает функцию двух переменных z(x,y) в неявном виде и
, то справедливы формулы

139
.
Пример 5. Найти производную функции у, заданной неявно уравнением
.
1 способ. В данном случае F(x,y)=
, находим и :
, .
находим
.
2 способ. Дифференцируем обе части уравнения
,
считая у функцией от х:
,
отсюда получим
.
Производная по направлению. Градиент. Если функция z = f(x; y)
имеет в точке М(x; y) непрерывные частные производные, то в этой точке
существует и производная по любому направлению, исходящему из точки М;
обозначается эта производная символом , где – вектор, задающий направле-
ние, и вычисляется по формуле:
,
и направляющие косинусы единичного вектора .
Градиентом функции z = f(x; y) в точке М(x; y) называется вектор, коорди-
наты которого равны соответствующим частным производным
,
вычисленным в точке М(x; y).
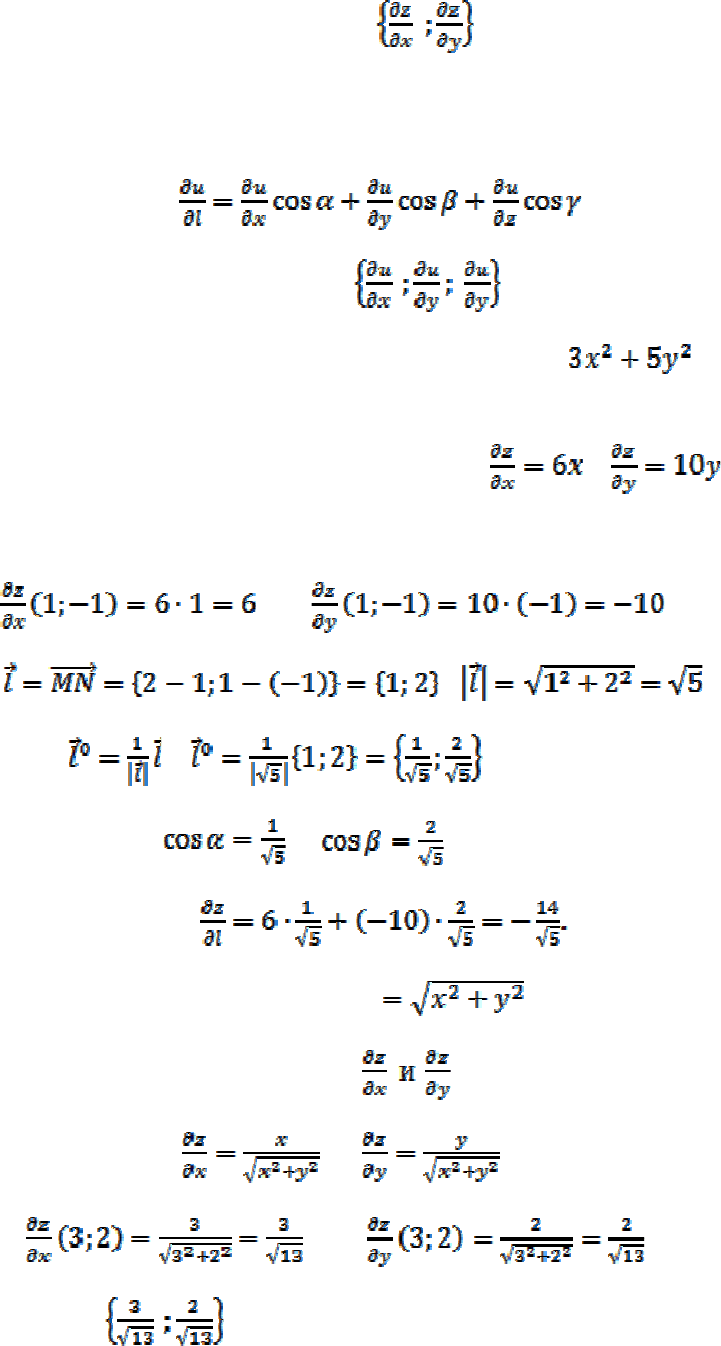
140
Градиент обозначается grad z(M)= .
Аналогично определяются производная по направлению и градиент для
функции трех переменных u = f(x; y;z) в точке М(x; y;z):
;
grad u(M)=
.
Пример 6. Вычислить производную функции z =
в точке М(1;
-1) по направлению к точке N(2;1).
Находим частные производные функции:
, .
Вычисляем значение этих производных в точке М(1; -1):
, .
Имеем
, ,
; .
Откуда следует, что
, .
Таким образом,
Пример 7. Найти grad z(M), если z
, М(3;2).
Находим частные производные
и их значения в точке М(3;2):
, ;
, .
grad z(3;2)=
.
Производные и дифференциалы высших порядков. Пусть дана функция
