Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

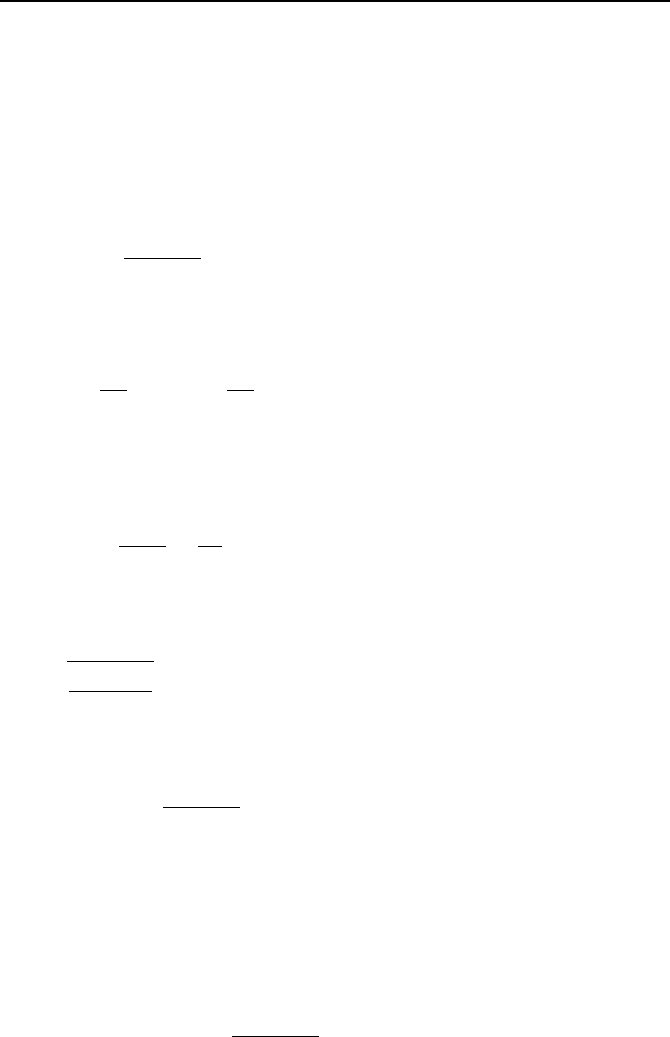
462 IVa. Heat Transfer: Conduction
Case 1. Temperature Boundary Condition. In this case, the inside and outside
temperatures are specified (i.e., T(r
1
) = T
1
and T(r
2
) = T
2
). Substituting these in
the cylinder temperature profile yields:
c
1
lnr
1
+ c
2
= T
1
c
1
lnr
2
+ c
2
= T
2
We find c
1
and c
2
from this set of equations. By back substitution in the tempera-
ture profile, we get:
)/ln(
)/ln(
)(
1
12
21
1
rr
rr
TT
TrT
−
−=
To find the rate of heat transfer, we use Fourier’s law for a region of the wall be-
tween r and r + dr:
d
r
dT
rLk
d
r
dT
kAQ )2(
π
−=−=
While temperature is a function of radius, the rate of heat transfer at steady state
remains constant at any radius. Hence, we rearrange Fourier’s law, and integrate
from inside r = r
1
to outside r = r
2
:
µ
¶
´
−=
³
2
1
2
1
2
r
r
T
T
r
dr
kL
Q
dT
π
Carrying out the integration, we find:
kL
rr
TT
Q
π
2
)/ln(
12
21
−
=
IVa.6.2
Using the electrical resistance analogy, we find that for cylinders, the thermal re-
sistance is given as:
R
s
=
kL
rr
R
cylinder
π
2
)/ln(
12
= IVa.6.3
Case 2. Convection Boundary Condition. Having derived the rate of heat transfer
between two radial locations in the cylinder and the corresponding thermal resis-
tance, we now consider the case where convection boundary conditions are speci-
fied for the inside and outside of the cylinder. To find the equation for tempera-
ture profile in the cylinder, we first find coefficients c
1
and c
2
by using the
convection boundary condition inside the cylinder:
0]
)(
[)]([
1
1
=
∂
=∂
−−=−
r
rrT
krrTTh
faa

6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 463
Substituting for temperature profile and its derivative we obtain;
0/)]ln([
11211
=++− rkccrcTh
faa
. Similarly, from the convection boundary
condition outside the cylinder we find that:
()
()
[]
0
2
2
=−−
∂
∂
−
=
=
fb
rr
b
rr
TrTh
r
rT
k
Substituting for temperature profile and its derivative, we obtain:
kc
1
/r
2
+ h
b
[(c
1
lnr
2
+ c
2
) – T
fb
] = 0
Solving these two equations for
c
1
and c
2
and substituting, we find the tempera-
ture profile in the cylinder as:
)/()/ln()/(
)/()/ln(
)(
2121
11
ba
a
fbfa
fa
hrkrrhrk
hrkrr
TT
TrT
++
+
−=
−
−
IVa.6.4
The inside surface temperature is:
)/()/ln()/(
)/(
)(
2121
1
1
ba
a
fbfa
fa
hrkrrhrk
hrk
TT
TrT
++
−=
−
−
Similarly, the outside surface temperature of the cylinder can be found as:
)/()/ln()/(
)/()/ln(
)(
2121
112
2
aa
a
fbfa
fa
hrkrrhrk
hrkrr
TT
TrT
++
+
−=
−
−
We can find the rate of heat transfer from an electrical analogy:
)2(
2
)/ln(
)2(
2
2
12
21
1
1
Lrh
Q
TT
kL
rr
Q
TT
Lrh
Q
TT
b
fb
a
fa
π
π
π
=−
=−
=−
Summing up, the intermediate temperatures cancel out. We then rearrange terms
to find
Q
as:
ba
fbfa
LhrkL
rr
Lhr
TT
Q
2
12
1
2
1
2
)/ln(
2
1
πππ
++
−
=
IVa.6.5

464 IVa. Heat Transfer: Conduction
Case 3. Steady State Heat Loss from Insulated Cylinders: This is similar to
Case 2. Insulation of piping systems is necessary in power production for exam-
ple, to reduce the rate of heat loss from the hotter fluid and in cryogenics to reduce
the rate of heat transfer to the fluid. To accomplish this, as shown in Fig-
ure IVa.6.2, pipes are encapsulated in layers of insulation made of materials with
low thermal conductivity. To determine the rate of heat transfer, we extend the
method of Case 2 by writing the boundary temperatures in terms of total rate of
heat transfer and the related thermal resistance and add them up to obtain:
ba
fbfa
LhrLk
rr
Lk
rr
Lhr
TT
Q
32
23
1
12
1
2
1
2
)/ln(
2
)/ln(
2
1
ππππ
+++
−
=
IVa.6.6
¦¦
=
−
=
+
1
1
1
2
)/ln(
n
i
i
ii
n
Lk
rr
R
π
¦
−
=
R
TT
Q
ba
bna
RRRR ++=
¦¦
aa
a
Ah
R
1
=
bb
b
Ah
R
1
=
,
,
L
T
fb
r
1
r
2
r
n
T
2
T
1
T
fa
T
n
T
fb
, h
b
R
b
R
n
R
1
R
a
k
2
k
1
Q
.
k
n
T
fa
, h
a
....
Q
.
T
fb
, h
b
T
fa
, h
a
Figure IVa.6.2. Reduction of heat loss through pipe wall with multiple layers of insulation
Example IVa.6.1. A layer of paint and 3 layers of insulators cover a pipe carry-
ing steam. Find the rate of heat loss to ambient.
No. Region d
i
(in) d
o
(in) k (Btu/ft·h·F)
1 Pipe 24.0 28.0 10.0
2 Paint 28.0 28.05 0.50
3 Insulator 28.05 40.0 0.03
4 Insulator 40.0 50.0 0.02
5 Insulator 50.0 55.0 0.01
Other data are specified as: T
f,a
= 650 F, h
a
= 500 Btu/ft
2
·h·F, h
b
= 5 Btu/ft
2
·h·F,
T
f,b
= 75 F, and L = 400 ft.
Solution: Thermal resistances from inside to outside are as follows:
Pipe bulk to wall: R
f,a
= 1./(
π
d
i
L)h
a
= 1./[
π
× (24/12) × 400 × 500] = 7.95E-7 h·F/Btu
Region 1: R
pipe
= ln(r
1
/r
i
)/(2
π
k
pipe
L) = ln(28/24)/[2 ×
π
× 10 × 400] = 6.13E-6 h·F/Btu
Region 2: R
paint
= ln(r
2
/r
1
)/(2
π
k
paint
L) = ln(28.05/28)/[2 ×
π
× 0.5 × 400] = 1.42E-6 h·F/Btu
Region 3: R
1
= ln(r
3
/r
2
)/(2
π
k
ins. a
L) = ln(40/28.05)/[ 2 ×
π
× 0.03 × 400] = 4.71E-3 h·F/Btu
Region 4: R
2
= ln(r
4
/r
3
)/(2
π
k
ins. b
L) = ln(50/40)/[ 2 ×
π
× 0.02 × 400] = 4.44E-3 h·F/Btu
Region 5: R
3
= ln(r
5
/r
4
)/(2
π
k
ins. c
L) = ln(55/50)/[ 2 ×
π
× 0.01 × 400] = 3.79E-3 h·F/Btu
6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 465
Loss to ambient: R
f,b
= 1./(
π
d
5
L)h
b
= 1./[
π
× (55/12) × 400 × 5] = 3.47E-5 h·F/Btu
ΣR = 7.95E-7 + 6.13E-6 + 1.42E-6 + 4.71E-3 + 4.44E-3 + 3.79E-3 + 3.47E-5 =
0.013 h·F/Btu
The thermal resistance is practically due to the three layers of insulation.
loss
Q
= (T
f,a
– T
f,b
)/ΣR = (650 – 75)/0.013 = 44,288 Btu/hr = 13 kW.
Note that if there was no insulation,
loss
Q
= (650 – 75)/(7.95E-7 + 6.13E-6 + 3.47E-5) = 4 MW!
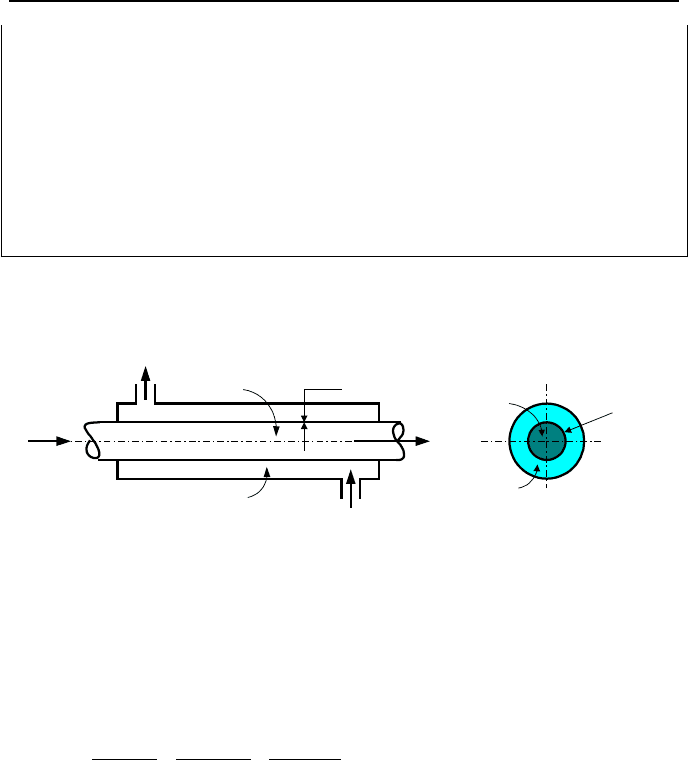
Let’s now consider the rate of heat transfer in a concentric or simple shell &
tube heat exchanger as shown in Figure IVa.6.3.
δ
= r
o
- r
i
h
i
, T
i
h
o
, T
o
δ
= r
o
- r
i
Shell-side
Tube-side
Figure IVa.6.3. Schematics of a concentric or simple shell & tube heat exchange
Applying the thermal resistance concept to this heat exchanger results in:
TUAQ ∆=
IVa.6.7
where
1
2
1
2
)/ln(
2
1
−
»
¼
º
«
¬
ª
++=
oos
io
ii
LhrLk
rr
Lhr
UA
πππ
IVa.6.8
In Equation IVa.6.8, U is called the “overall heat transfer coefficient.” The value
of U is based on the area it is associated with so that
)2()2( LrULrUUA
ooii
ππ
==
where U
i
and U
o
are referred to as the overall heat transfer coefficients based on
the inside and outside tube diameter, respectively. Hence, U
o
becomes:
[]
1−
++=
osio
RRRU IVa.6.8-1
where R
i
= (1/h
i
)(d
o
/d
i
), R
s
= ln(d
o
/d
i
)/[d
o
/(2k
s
)], and R
o
= 1/h
o
where k
s
is thermal
conductivity of the tube metal. Substituting we find;

466 IVa. Heat Transfer: Conduction
1
1
2
)/ln(
−
»
¼
º
«
¬
ª
++=
os
ioo
ii
o
o
hk
ddd
hd
d
U
IVa.6.8-2
The overall heat transfer coefficient is an essential factor in the design and opera-
tion of heat exchangers.
6.2. 1-D S-S Heat Conduction in Solid Cylinders (
0≠
′′′
q
)
Solution for steady state temperature distribution in the axial direction in solid cyl-
inders without internal heat generation is given by Equation IVa.5.2. This equa-
tion is applicable to an axially-insulated solid cylinder of length 2L where heat is
added to one end and removed from the other end. The solution to steady state
heat conduction in the radial direction for solid cylinders without internal heat
generation is trivial as the solid cylinder has to be at uniform and constant tem-
perature at any cross section. Considering cylinders with internal heat generation,
our goal is to find the steady state temperature profile for two cases of solid and
hollow cylinders. For the case of solid cylinders we analyze fuel rods in nuclear
reactors. For hollow cylinders, we find temperature distribution in an annular fuel
rod where coolant flows both inside and outside of the rod. The governing equa-
tion for both cases is Equation IVa.2.10 with
∂
T/
∂
t = 0.
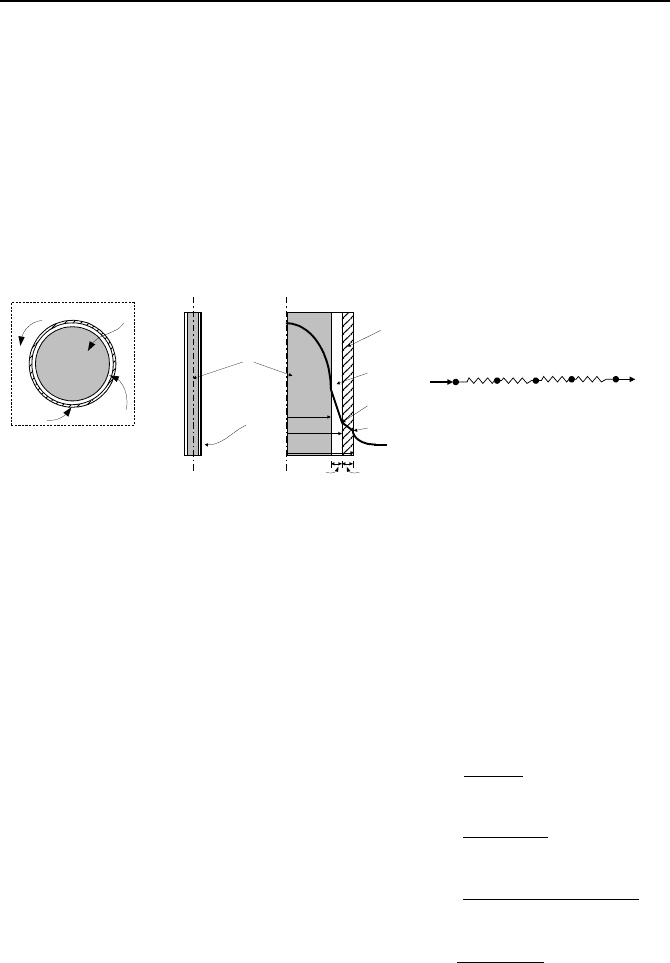
For solid cylinders with internal heat generation we study temperature distribu-
tion in a nuclear fuel pellet. For light water reactors, such pellets are made of ura-
nium dioxide (UO
2
). A nuclear fuel rod (see Chapter I) consists of stacks of such
pellets contained within cladding. Nuclear heat is produced when fuel rods in the
core are exposed to neutron flux. In the discussion below, we analyze two cases.
In Case 1 we consider a bare fuel rod to determine thermal resistance of a pellet.
In Case 2 we analyze a fuel rod with cladding.
Case 1. Nuclear Fuel Pellet. Typical fuel pellet for PWRs is a right circular
cylinder with both diameter and height being about 1 cm. The active length of a
fuel rod is about 3.6 m or 144 in so that a fuel rod has as over 300 fuel pellets. To
derive the thermal resistance of a fuel rod, let’s assume that a bare rod is placed in
the core. To find thermal resistance, we find the temperature gradient of the fuel
(i.e., T
F1
– T
F2
):
0)(
1
=
′′′
+ q
d
r
dT
rk
d
r
d
r
F
F
IVa.6.9
Fuel
T
F1
T
F2
r
F
q'''
.
Figure IVa.6.4. A solid cylinder with internal volumetric heat generation

6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 467
Thermal conductivity of UO
2
is temperature dependent however, replacing it with
an average value allows us to integrate Equation IVa.6.9:
³³
′′′
−= rdr
k
q
dr
dT
rd
F
F
)(
This results in:
r
c
r
k
q
dr
dT
F
F 1
2
+
′′′
−=
Upon further integration we obtain:
21
2
)ln(
4
)( crcr
k
q
rT
F
F
++
′′′
−=
IVa.6.10
Coefficients c
1
and c
2
are found from boundary conditions. Coefficient c
1
must be
zero for two reasons. First, at r = 0, temperature must be finite. Second, due to
symmetry, temperature is a maximum at the centerline. Coefficient c
2
is found
from temperature T
F
(r = 0) = T
F1
, resulting in a temperature profile of:
2
1
4
)( r
k
q
TrT
F
FF
′′′
−=
Temperature gradient across the bare fuel rod is obtained by finding temperature
at r = r
F
:
2
21
4
F
F
FF
r
k
q
TT
′′′
=−
IVa.6.11
Relating
q
′′′
to the rate of heat transfer according to QqLr
F
=
′′′
)(
2
π
and substitut-
ing in Equation IVa.6.11 yields:
F
FF
F
r
TT
AkQ
21
2
−
=
IVa.6.12
Where, in Equation IVa.6.12, A =
π
r
F
L is the surface area. Thermal resistance of a
pellet is found as:
1
24
F
F
FF
r
R
kA Lk
π
== IVa.6.13
Note that by substituting for the volumetric heat generation rate in Equa-
tion IVa.6.11, we find:
FF
FF
k
q
Lk
Q
TT
ππ
44
21
′
==−
IVa.6.14
468 IVa. Heat Transfer: Conduction
Equation IVa.6.14 is now in terms of the linear heat generation rate and shows that
temperature difference across the fuel is only a function of
q
′
(the linear heat gen-
eration rate) and is independent of fuel diameter. The linear heat generation rate is
a key factor in the design and operation of nuclear plants.
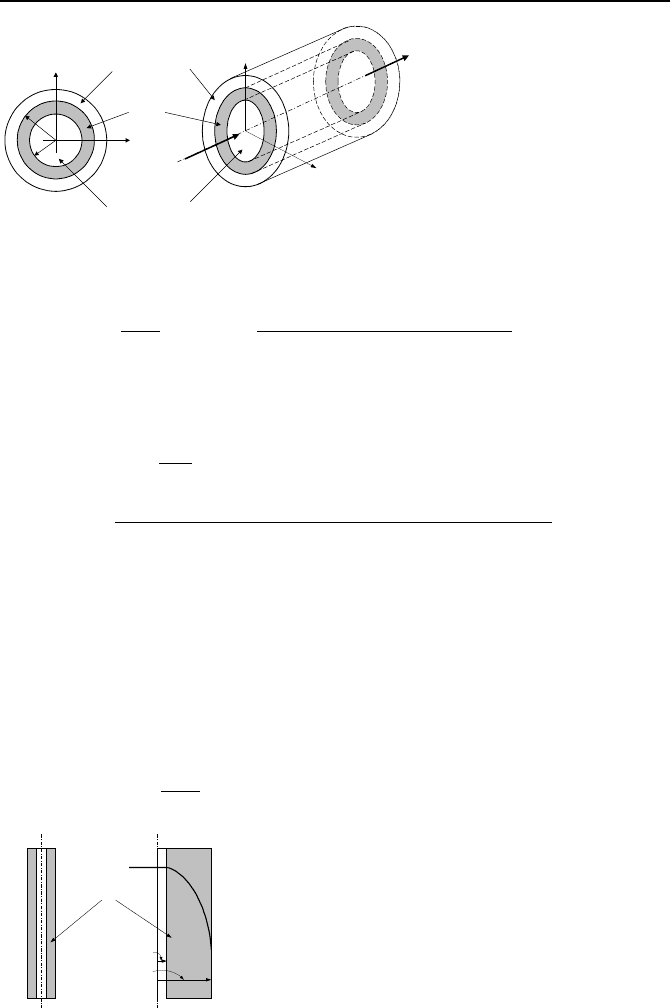
Case 2. Nuclear Fuel Rod. A fuel rod of a light water reactor consists of a hol-
low cylinder made of Zircaloy, filled with UO
2
pellets. The cylinder is about 12 ft
long (Figure IVa.6.4). The space between the fuel and the clad is referred to as
gap, being originally filled with helium and pressurized to several hundred psi.
Fission gases released during the nuclear reaction also diffuse into the gap region
further pressurizing the rod.
Coolant
Fuel
Clad
Gap
Fuel
Clad
Gap
T
F1
T
F2
T
C1
T
C2
T
f
, h
f
r
C2
r
F
r
C1
T
f
, h
f
Q
.
Q
.
T
F1
T
F2
T
C1
T
C2
T
f
R
F
R
G
R
C
R
f
δ
G
δ
C
Figure IVa.6.5. Temperature profile in a cylindrical fuel rod
Our goal is to find the rate of steady state heat transfer. Due to symmetry, we
consider temperature distribution only in one half of the fuel rod. At steady state
operation, the rate of heat transfer is the same in all the fuel rod regions, the fuel
pellet region, the gap region, and the cladding region. We use subscript F for fuel,
C for cladding, G for Gap, and f for the coolant. To find the rate of heat transfer in
each region, we use Fourier’s law but rearrange the equation in terms of tempera-
ture difference. Starting from the fuel centerline and moving toward the coolant,
the rate of heat transfer in each region of fuel, gap, cladding and coolant becomes:
Temperature gradient in fuel:
F
FF
Lk
Q
TT
π
4
21
=−
Temperature gradient in gap:
GC
CF
Lhr
Q
TT
1
12
2
π
=−
Temperature gradient in clad:
[]
)/ln(/2
12
21
CCC
CC
rrLk
Q
TT
π
=−
Temperature gradient in coolant:
fC
fC
Lhr
Q
TT
2
2
2
π
=−
Summing up these relations, the intermediate temperatures cancel out and after re-
arrangement we get:

6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 469
fCC
CC
GG
F
fF
LhrLk
rr
Lhr
R
TT
Q
2
12
1
2
1
2
)/ln(
2
1
πππ
+++
−
=
IVa.6.15
where in Equation IVa.6.15, R
F
is given by Equation IVa.6.13 and r
G
and h
G
are
effective gap radius and heat transfer coefficient, respectively.
Example IVa.6.2. Find the centerline temperature of an average fuel rod in a
PWR core.
Parameter Value Parameter Value
Core power (MW): 2700 Clad inside diameter (in): 0.388
Number of fuel rods: 38,000 Gap thickness (in): 0.0075
Fuel rod length (ft): 12.2 Water temperature (F): 575
Clad outside diameter (in): 0.44 h
f
(Btu/ft
2
·h·F): 6000
k
F
& k
C
(Btu/ft·h·F): 1 & 3 h
G
(Btu/ft
2
·h·F): 1000
Solution: We find d
C2
= 0.44 in, d
C1
= 0.388 in and d
F2
= d
C1
– 2
δ
Gap
= 0.194 – 2
× 0.0075 = 0.373 in
We now find the individual thermal resistances in Equation IVa.6.15:
R
F
= 1/(4
π
Lk
F
) = 1/(4 ×
π
× 12.2 × 1) = 6.53E-3 h·F/Btu
R
G
= 1/(2
π
r
F1
Lh
G
) = 1/[(0.373/12) ×
π
× 12.2 × 1000] = 8.39E-4 h·F/Btu
R
C
= ln(r
C2
/r
C1
)/(2
π
Lk
C
) = ln(0.44/0.388)/[2 ×
π
× 12.2 × 3]= 5.47E-4 h·F/Btu
R
f
= 1/(2
π
r
C2
Lh
f
) = 1/[(0.44/12) ×
π
× 12.2 × 6000] = 1.18E-4 h·F/Btu
ΣR = 6.53E-3 + 8.53E-4 + 5.56E-4 + 6.03E-5 = 8E-3 h·F/Btu
The fuel centerline temperature is found from:
Q
= (T
F1
– T
f
)/ΣR
where total core power is: Q
= (2700 × 1000 × 3412)/38000 = 0.2424E6 Btu/h
0.2424E6 = (T
F1
– 575)/8E-3. Solving for T
F1
, we find T
F1
= 2514 F
6.3. 1-D S-S Heat Conduction in Hollow Cylinders ( 0≠
′′′
q
)
An annular nuclear fuel pellet is a good example for a hollow cylinder with inter-
nal heat generation. In this section, we analyze three cases of such fuel pellets.
Case 1. Two-Stream Coolant. Shown in Figure IVa.6.6 is the conceptual de-
sign of an annular fuel rod. Fluid flows both around the fuel (similar to a solid
fuel rod) and through the central channel for further cooling. Our goal is to deter-
mine the temperature distribution in the fuel pellet. We use Equation IVa.6.10
while assuming an average thermal conductivity for the fuel. To find the coeffi-
cients c
1
and c
2
, we must use either of the following boundary conditions:
Surface Temperatures Specified. For specified fuel surface temperatures at r
i
and r
o
(i.e., T
Fi
and T
Fo
) we find the coefficients and upon substitution in Equa-
tion IVa.6.10, temperature profile in the bare annular fuel becomes:
470 IVa. Heat Transfer: Conduction
Inner Channel
Outer Channel
Fuel
T
fi
, h
i
T
fo
, h
o
r
i
r
o
x
y
x
y
Figure IVa.6.6. A conceptual annular fuel rod with neither inner nor outer cladding
)/ln(
)/ln(
))(4/(
)(
4
)(
22
22
i
io
iFFiFo
i
F
FiF
rr
rr
rrkqTT
rr
k
q
TrT
−
′′′
+−
+−
′′′
−=
IVa.6.16
Convection Boundary Specified. For specified convection boundary, tempera-
ture distribution in the fuel is:
22
22
() ( )
4
(/4)( )(/2)(/ /)
ln( / )
(1 / 1 / ) ln( / )
FFi i
F
Fo Fi F o i F i i o o
i
Fii oo oi
q
Tr T r r
k
TTqkrr qkrhrh
rr
krh rh rr
′′′
=− −+
−− −− +′′′ ′′′
++
Case 2. One-Stream Coolant. In this case, the annular fuel pellets are encased
inside the clad and the fuel rod is cooled only by coolant flowing around the clad.
To calculate the annular fuel thermal resistance, we consider the case of power
production in a bare annular fuel rod. The answer to this case is also given by
Equation IVa.6.10. To find coefficients c
1
and c
2
we use the following boundary
conditions. At r = r
F1
, there is no heat flux, hence 0/)(
1
=drrdT
FF
and at r = r
F1
,
we have T(r) = T
F1
. Using these boundary conditions, temperature distribution in
the fuel becomes:
])/ln()[(
4
)(
2
1
2
1
2
1
2
1 FFF
F
FF
rrrrr
k
q
TrT −−
′′′
−=−
Fuel
T
F1
T
F2
r
F1
r
F2
q
′′′
We can now calculate temperature gradient across the fuel pellet by taking r = r
F2
to obtain:

6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 471
]ln)1[(
4
222
2
2
21
ζζζ
+−
′′′
=−=∆
F
F
FF
k
rq
TTT
where
21
/
FF
rr=
ζ
. The volumetric heat generation rate is related to the rate of
heat transfer from a bare annular fuel as:
)1()(
22
2
2
1
2
2
ζππ
−
′′′
=−
′′′
= LrqLrrqQ
FFF
Substituting for the volumetric heat generation rate in terms of the rate of heat
transfer and rearranging:
()
F
Lk
T
Q
π
ζ
ζζ
4/
1
ln
1
2
22
¸
¸
¹
·
¨
¨
©
§
−
−
∆
=
IVa.6.17
Thus, thermal resistance of an annular fuel cooled only from outside is therefore
given by:
()
F
LkR
π
ζ
ζζ
4/
1
ln
1
2
22
¸
¸
¹
·
¨
¨
©
§
−
−=
IVa.6.18
If we compare Equation IVa.6.18 with Equation IVa.6.14 derived for a solid fuel,
we conclude that for the same thermal conductivity and linear heat generation rate,
the annular fuel operates at a lower temperature gradient. Similarly, for the same
temperature gradient and thermal conductivity, the annular fuel can be operated at
higher linear heat generation rate:
'
'
SolidFuel
lAnnularFue
q
q
R
=
=
2
22
1
)ln1(1
ζ
ζζ
−
+−
Case 3. Annular Fuel Rod consists of annular fuel pellets inside a clad as
shown in Figure IVa.6.7. The rate of heat transfer is obtained from Equa-
tion IVa.6.15 but with
R
F
given by Equation IVa.6.18.
Fuel
Clad
Gap
T
F1
T
F2
T
C1
T
C2
T
f
, h
f
r
C2
r
F2
r
C1
δ
C
δ
G
T
F1
T
F2
T
C1
T
C2
T
f
R
F
R
G
R
C
R
f
Q
.
T
f
, h
f
r
F1
Q
.
Figure IVa.6.7. Annular fuel rod with cladding
