Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

442 IVa. Heat Transfer: Conduction

tion and heat added to the boundary by radiation are carried away from the bound-

ary by convection. In case (c), heat brought to the boundary by convection and

heat added to the boundary by radiation are carried away from the boundary by

conduction. For case (b), for example, an energy balance gives:

0)()/( =−−

′′

+∂∂−

fbrb

TThqnTk



As seen from this example, Kirchhoff’s law also applies for steady state condi-

tions, similar to the flow of electricity or flow of fluids in piping networks.

It is important to take advantage of any existing symmetrical condition for the

temperature profile. This generally happens for substances having familiar ge-

ometry such as plate, parallelepiped, cylinder, or sphere as shown in Fig-

ure IVa.2.3. For uniform internal heat generation and external heat removal, we

note that in the case of a plate, dT/dx = 0 at x = 0 and in the case of a cylinder and

sphere, dT/dr = 0 at r = 0. This also implies that for a plate, for example, the mid-

plane is at an adiabatic condition.

Cylinder

Plate

Sphere

′′



′′



′′



Figure IVa.2.3. Symmetrical temperature profiles in plates, cylinders, and spheres

Conduction BC is applied between two bodies. Equal temperature and equal

heat flux apply at the point of contact so that for bodies A and B in perfect contact,

= T

and –k

/dn = –k

/dn.

Initial condition (IC) is required to find a solution for problems involving tran-

sient conduction because to find temperature at other points in time, temperature

distribution in the substance must be known at time zero. If the time zero distribu-

tion is given as

)(

, the solution must satisfy

(, 0) ()Trt T r==

2.2. Determination of Heat Conduction in Various Dimensions

While heat conduction in solids is generally three dimensional, we often encounter

cases in practice that conduction may be considered predominantly two or even

one dimensional. The dimensionless number most helpful in this regard is the

Biot number.

2. The Heat Conduction Equation 443

Biot number (Bi = R

cond

conv

=hL

/k), after J. B. Biot, is the ratio of two ther-

mal resistances. Considering a solid with a convection boundary condition at its

surface, the numerator is thermal resistance to conduction within the solid and the

denominator is thermal resistance to convection across the fluid boundary layer.

Also h, k, and L

are heat transfer coefficient, thermal conductivity of a solid, and

a characteristic length, respectively.

Lumped formulation of heat conduction is often used in evaluating the tem-

perature response of objects to changes in the environmental temperature. This is

the simplest type of analysis, providing useful information. On the other hand,

since the entire object is represented by only one temperature, no knowledge about

temperature distribution in the object can be obtained. Conditions for the applica-

bility of the lumped-thermal capacity formulation are discussed in Section 3.

One-dimensional (1-D) heat conduction generally provides sufficient infor-

mation about temperature distribution, and is the most commonly used technique

in engineering applications. Due to the symmetry and large dimensions in two of

the three directions in most cases, application of a 1-D analysis not only is a sim-

plifying but also a reasonable assumption. Examples of such cases are shown in

Figure IVa.2.4. A plate also referred to as a slab, is a solid, which is limited only

in the x-direction. A long, slender cylinder is another example for which a 1-D

conduction for obtaining temperature distribution is a reasonable assumption. In

these solids, it is reasonable to assume that T = f(x) and T = f(r), respectively.

Figure IVa.2.4. Solids suitable for 1D heat conduction, a plate (slab) and a long slender

rod

Regarding the latter example, let’s consider the thin, solid cylinder of Fig-

ure IVa.2.5(a). If heat in this long solid cylinder is being generated uniformly

while exposed to a convection boundary, the diffusion of heat is in the radial di-

rection and for a given r, temperature is the same at any axial location (any x).

Now let’s assume that the solid cylinder is of finite length and rather than heat is

being generated in the cylinder, it is added at one end as shown in Fig-

ure IVa.2.5(b). If this thin cylinder is fully insulated, the heat diffusion is basi-

cally in the axial direction. In this cylinder, for a given x, temperature is practi-

cally the same across any cross section.

444 IVa. Heat Transfer: Conduction

Insulation

′′′

h, T

hot

cold

0< r < R

0< x < L

(a) (b)

Figure IVa.2.5. One-dimensional heat conduction; (a) T = f(r) and (b) T = f(x)

Example IVa.2.3. Find the rate of heat transfer if the cylinder in Figure IVa.2.5(b)

is a stainless steel rod.

k = 15 W/m·K (8.7 Btu/h·ft·F), L = 1 m (3.3 ft), T

= 200 C (392 F), T

= 100 C

(212 F), A = 5 cm

(0.8 in

Solution:

SI BU

−

−×=

∆

100200

)4E5(15

kAQ



0.75 W

−

3.3

212392

)144/8.0(7.8

2.6 Btu/h

Two- and three-dimensional heat conduction must be used when an object

cannot be accurately analyzed with the one-dimensional heat conduction method.

For example, temperature distribution in a short, fat cylinder and in a parallelepi-

ped, as shown in Figure IVa.2.6 requires a two- and a three-dimensional analysis,

respectively. In these solids, temperature distribution is given as T = f(x, r) and

T = f(x, y, z), respectively. In multi-dimensional problems, it is essential to choose

a coordinate system that best fits the object geometry.

Figure IVa.2.6. Solids requiring multi-dimensional heat conduction, a short cylinder and a

parallelepiped

3. Analytical Solution of Heat Conduction Equation

Due to the importance of analytical solutions, this topic is discussed first, followed

by the discussion of numerical solutions. One of the important aspects of seeking

analytical solutions is the fact that it enhances our intuition about the nature of the

problem. The understanding of how to formulate a problem, what to expect, and

how to interpret the results becomes an asset when using numerical methods for

problems that are not amenable to analytical solutions. The term analytical solu-

tion refers to a solution found by mathematical modeling of the problem, which

4. Lumped-Thermal Capacity Method for Transient Heat Conduction 445

provides an exact answer. Despite our preference to seek analytical solutions in

closed form, and the availability of many mathematical techniques for solving

problems in conduction heat transfer, analytical solutions are not always possible.

This is due to the involved complexities such as multi-dimensional conduction in

complex geometries with temperature dependent properties. In such cases, nu-

merical methods are employed. The disadvantage of numerical methods is that

every problem has to be modeled and solved separately. Analytical solutions not

only provide exact answers in most cases, but may also provide applicable solu-

tions to groups of similar problems. Another advantage of analytical solutions is

in verifying the correctness and accuracy of numerical solutions of problems for

which analytical solutions can be found.

Even if analytical solutions exist, for the sake of simplicity, there are occasions

where we settle for solutions with some degree of approximation. For example,

we can find an infinite series solution for temperature distribution as a function of

time in a slab. If Fo > 0.2, we can show that the transient temperature distribution

in the slab can be approximated by only the first term of the infinite series.

In the foregoing discussions, both steady state and transient problems are dis-

cussed. This allows us to learn about the inherent differences. We begin the dis-

cussion with the lumped formulations and proceed to one, two, and three-

dimensional problems in various coordinates.

4. Lumped-Thermal Capacity Method for Transient Heat Conduction

The lumped-thermal capacity method is a convenient means of solving transient

conduction problems. The term lumped implies that temperature distribution in

the object is not a concern since the entire object is represented by only one tem-

perature. This method of analysis is useful when we need to estimate the tempera-

ture response of an object suddenly exposed to a different temperature. By tem-

perature response, we mean the change in temperature of the object as a function

of time. To derive the relation for temperature versus time, consider the object

shown in Figure IVa.4.1. This object is initially at a temperature of T

when is

suddenly exposed to a temperature of T

. In this derivation, we make two impor-

tant assumptions: a) the medium temperature T

remains constant and is not af-

fected by the energy transfer with the object and b) heat transfer between the ob-

ject and the medium is due only to heat convection from the object to the medium.

To find the governing equation, we may derive the equation directly from the con-

servation equation for energy, using the control volume as shown in Fig-

ure IVa.4.1. If the body is hotter than the environment (T

> T

), then the rate of

internal energy depletion of the object is due to the heat loss to the environment.

, h

, c, A,V

Figure IVa.4.1. Sudden exposure of an object to a lower or higher temperature medium

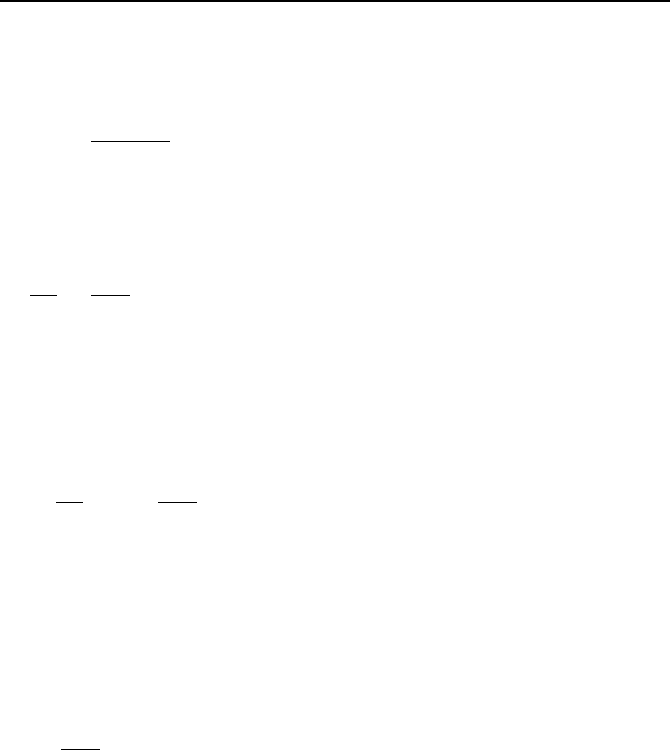
446 IVa. Heat Transfer: Conduction

Using Equation IIa.6.4 where

¦¦¦

′′′

=== 0qWhmhm

eeii





and

−=



we obtain:

Tcd

)V(

=−



where ,, c

V, and T are density, specific heat, volume and temperature of the ob-

ject, respectively. If we substitute for the convection heat transfer,

)(

TThAQ −=



, we obtain:

[]

)(

TThA

cdt

−−=

IVa.4.1

where h and A are the heat transfer coefficient at the boundary and the heat trans-

fer area of the object, respectively. To find the solution to this first order linear

differential equation, we may introduce a change in function as

TT −=

. Since

remains constant dT/dt = d(T – T

)/dt = d

/dt. Substituting for T in terms of

Equation IVa.4.1 and integrating yield:

³³

−=

hAd

)

(

ρθ

where

is obtained by applying the initial condition T(t = 0) = T

. Thus,

= T

– T

is a known value. We find the object temperature as a function of time by

carrying out the integral and substituting for

and

in terms of T , T

, and T

)()(

eTTTtT

−

−+= IVa.4.2

where the constant in this solution represents:

= IVa.4.3

Note that

, known as the time constant of the object, depends on both properties

of the object (density, specific heat, and geometry) and heat transfer coefficient at

the boundary. The time constant indicates how quickly an object responds to a

change in temperature. The numerator has units of energy per temperature and

1/hA represents thermal resistance. We can also derive a similar equation when

the object is colder than the surroundings (T

< T

), as shown in last graph of Fig-

ure IVa.4.1. Whether the object is colder or warmer than the surroundings to

which it is suddenly exposed, the object temperature reaches the temperature of

the surroundings asymptotically.

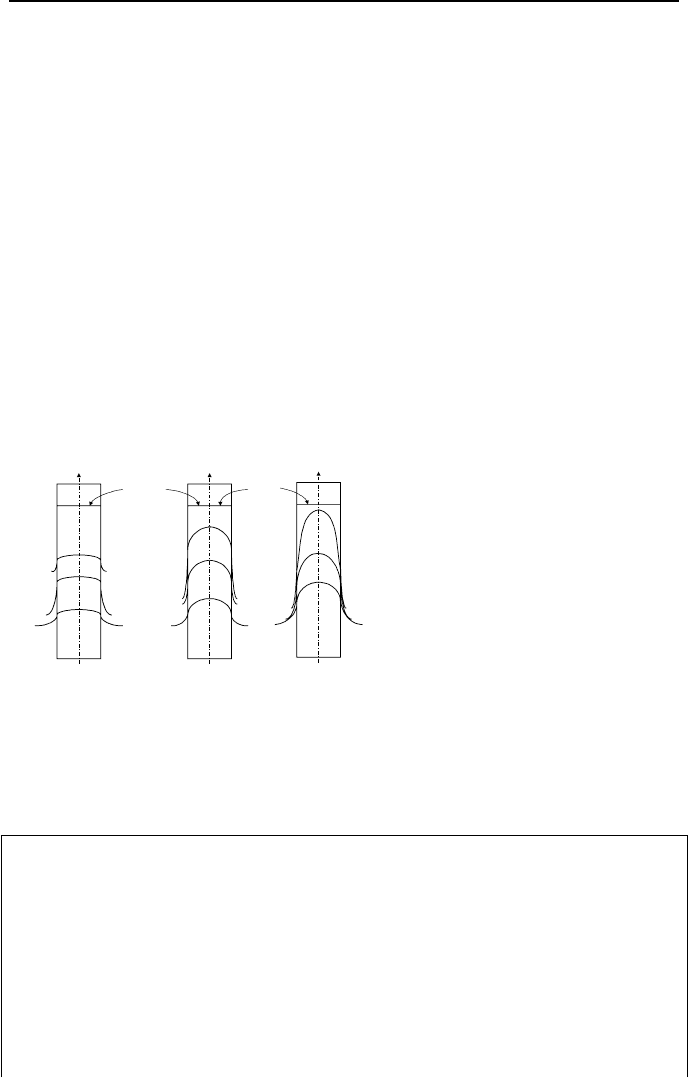
4. Lumped-Thermal Capacity Method for Transient Heat Conduction 447

The absolute value of the exponent in Equation IVa.4.2 increases with time re-

sulting in the exponential term to diminish and temperature of the object to even-

tually reach T

. The major assumption that allowed us to use this simple transient

analysis is the uniform temperature distribution within the object. This in turn im-

plies that the Biot number is much smaller than unity (i.e., the resistance to con-

duction is much smaller than the resistance to convection). Generally, for the

lumped capacitance analysis to be valid, we should have Bi = h(V/A)/k < 0.1.

The characteristic length appearing in the numerator of the Biot number for a slab

is half of the slab thickness, for a long cylinder is half its radius, and for a sphere

is one third of its radius.

Shown in Figure IVa.4.2 are three geometrically identical slabs (k

>> k

)

initially at temperature T

and suddenly exposed to a convection boundary condi-

tion of h and T

. Temperature gradients for these slabs are presented as functions

of both space and time. In the first slab, thermal conductivity is so high that tem-

perature anywhere within the slab can reasonably be considered the same. In the

second slab, thermal conductivity is smaller by a factor of 10. We see that tem-

perature varies noticeably within the slab. In the third slab, thermal conductivity

is smaller by a factor of 100. In this case, temperature varies markedly within the

slab.

-L

Bi >> 1

Bi << 1

Bi 1

Figure IVa.4.2. Comparison of temperature profile in slabs with different Biot numbers

To determine the temperature response of objects with large Biot numbers, we

need to use the conduction equation in one or more dimension as discussed later in

this chapter.

Example IVa.4.1. A piece of copper wire is initially at 150 C when suddenly

immersed in an environment at 38 C. Find the wire temperature after 1 minute, a)

if the environment is water and b) if the environment is air. Assume highly pol-

ished copper (

= 0.02) so that heat transfer is primarily due to convection.

Data: For copper at 150 C; k = 374 W/m·K, c = 381 J/kg·K, and

= 8938 kg/m

Wire diameter is 1 mm, and the heat transfer coefficient for water and air is h = 50

W/m

·K and h = 5 W/m

·K, respectively.

Solution: We first calculate the Biot number:

Bi = h(V/A)/k = h[(

L/4)/(

dL)]/k = hd/4k = 50 × (1/1000)/(4 × 374) = 3.3E-5

448 IVa. Heat Transfer: Conduction

Since Bi << 1 we can use the lumped capacitance method. For immersion in wa-

ter:

)V/(hAc

ρτ

= = 8938 × 381 × (

/4)L/[50 × (

d)L] = 17 s.

T = 38 + 112 × exp(–1 × 60/17) = 41 C

For exposure to air:

) = 170 s and T = 38 + 112 × exp(–60/170) = 117 C.

5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab

Our goal in this section is to solve the conduction equation in one-dimension (1-

D) in Cartesian coordinates under steady state (S-S) condition with and without in-

ternal heat generation. In the subsequent sections, we solve 1-D, S-S problems in

cylindrical and spherical coordinates. We then extend the solution method to

multi-dimensional transient problems.

By 1-D we mean that the geometry of the object and the specified boundary

conditions are such that the rate of heat transfer is predominantly one-dimensional

and is negligible in the other two dimensions.

5.1. 1-D S-S Heat Conduction in Slabs (

′′′



)

The goal is to find the steady state (

0/ =∂∂ tT ) temperature distribution in a slab

with constant thermal conductivity (

0/ =∂∂ Tk ) and with no internal heat genera-

tion (

′′′



). Recall that we defined a slab as a plate with a finite dimension

along the x-axis and infinite dimensions along the y- and z-axis. Applying the

Cartesian coordinate system to the slab and for the one-dimensional heat transfer,

the Laplacian simplifies to:

)(

T ==∇

IVa.5.1

Substituting in Equation IVa.2.4 and simplifying terms that drop due to steady

state and no internal heat generation, we get d

T/dx

= 0. The solution to this

problem is readily found to be T = c

x + c

where coefficient c

and c

can be

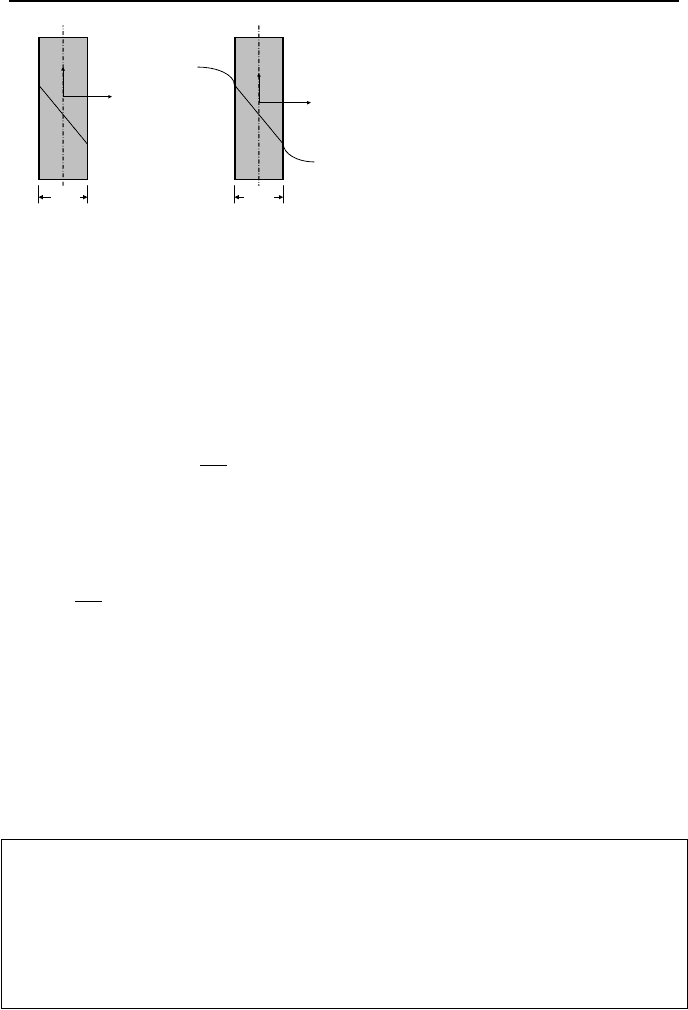
found by applying the boundary conditions. If surface temperatures are specified

(Figure IVa.5.2(a)), the equation for temperature distribution inside the slab is de-

termined as:

)(

2121 ssss

TTT ++−−= IVa.5.2

In this case, we can find the rate of heat transfer from the slab as

(/)qkAT x=∆∆



()/2

kA T T L=− .

5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 449

, T

(a) (b)

Figure IVa.5.2. (a) Slab with specified surface temperature and (b) Slab with a specified

convection BC

For the case that convection heat transfer is specified at the boundaries, Fig-

ure IVa.2.1(b), determination of the constants is more involved. At x = –L, con-

vection heat enters the node while conduction heat leaves the node, hence a heat

balance at the left boundary according to our sign convention, yields:

0)( =

∂

−−−

−=

−

Laa

kTTh

At the right boundary, heat by conduction enters the node while heat by convec-

tion leaves the node:

0)( =−−

∂

−

bLb

TTh

Substituting for temperature and its derivative, constants c

and c

are determined

as c

= –h

– T

)/c

and c

= T

– [h

(k + Lh

)(T

– T

)/c

] where c

= h

(k +

) + h

(k + Lh

). Regardless of the type of the boundary condition, the tempera-

ture profile in a one-dimensional slab with constant k at steady state and no inter-

nal heat generation is always a straight line. The rate of heat transfer for Fig-

ure IVa.5.2(b) where a convection boundary is specified is still given by

)/()(

xTTkAQ

∆−=



where, in this case Lx 2=∆ .

Example IVa.5.1. Heat loss through an insulation (k = 0.05 W/m·C) is 125 W/m

The temperature gradient across the insulation is 100 C. Find the thickness of the

insulation.

Solution: From Fourier’s law of conduction we have:

xTTkAQ

∆−== /)(125/



. Substituting for k and ∆T, the thickness is found

from 125 = 0.05 × 100/∆x. Therefore, ∆x = 0.04 m = 4 cm.

In the next example, we examine temperature distribution in a plate, given the

plate surface temperatures.

450 IVa. Heat Transfer: Conduction

Example IVa.5.2. Surface temperature at the mid-plane of a carbon steel plate (k

= 30 Btu/h·ft·F) is maintained at 250 F. The plate thickness is 1 in and surface

heat flux is 3250 Btu/h·ft

. Find the temperature of each face of this plate.

Solution: The temperature profile is linear, T = c

x + c

. If the plate thickness is

2L and x is on the left surface, at x = L, T = T

and at x = 0,

0)/(

′′

dxdTkq



. Solving for c

and c

to get ))(/( xLkqTT

−

′′



where mp stands for mid-plane. We then find T

(x = 0) )/( kLqT

′′



and

(x = 2L) )/( kLqT

′′

−=



An alternative solution is to use T

+ T

= 2T

and xTkq ∆∆=

′′



, where x∆ =

2L. Substituting values, we find T

+ T

= 500 and T

– T

= 3250 × (1/12)/30.

Solving this set, we obtain T

= 254.5 F and T

= 245.5 F.

Thermal conduction in slabs subject to the convection boundary condition is

solved in the next example.

Example IVa.5.3. A 1 in thick plate (k = 30 Btu/h·ft·F) separates two rooms. The

ambient temperature and associated heat transfer coefficient in one room are 150 F

and 25 Btu/h·ft

·F, respectively. The other room is at 50 F with a heat transfer co-

efficient of 15 Btu/h·ft·F. Find surface temperatures of the plate, temperature at

the mid-plane, and heat flux through the plate between the rooms.

Solution: Temperature distribution in the plate is given as T = c

x + c

)()(

3 abba

LhkhLhkhc +++= = 25(30 + 15 × 0.5/12) + 15(30 + 25 × 0.5/12) =

1231.25

/)( cTThhc

baba

−−= = –25 × 15(150 – 50)/1231.25 = –30.46 F/ft

[]

/))(( cTTLhkhTc

baaba

−+−= = 150 – [15(30 + 25 × 0.5/12)(150 –

50)/1231.25] = 112.18 F

T = –30.46x + 112.18

Having the temperature profile, we find the surface temperatures; at x = –0.5/12 =

–0.042 ft, T

–L

= 113.45 F and at x = 0.5/12 = 0.042 ft T

= 110.91 F. At the mid-

plane T

x = 0

= 112.18 F.

Heat flux is found from xTkq ∆∆=

′′



where, T

– T

= 2.54 F, thus

′′



30 × 2.54/(1/12) = 914.4 Btu/h·ft

The rate of heat transfer for Figure IVa.5.2(b) where the convection boundary

condition is specified can be found from an electrical engineering analogy

−



IVa.5.3

5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 451

where

++=

bslaba

RRRR

In this relation, the thermal resistance of the slab is R

slab

= ∆x/kA. For the convec-

tion boundary, thermal resistances for the left and the right boundaries are R

1/h

A and R

= 1/h

A, respectively. Substituting, we can find the rate of heat

transfer as:

AhkA

∆

−



IVa.5.4

The concept of thermal resistance becomes even more helpful in problems involv-

ing a multi-layer wall.

For example, consider a composite wall in series (Figure IVa.5.3). In general,

layers may consist of stacked conductors, as shown in Figure IVa.5.4. In such

cases, we should use parallel thermal resistance as the flow of heat is divided be-

tween the stacks so that the stack with least thermal resistance conducts more heat.

−



bna

RRRR +

¦¦

n-1

, h

n-1

...

Figure IVa.5.3. Composite wall, all layers arranged in series

++++=

RRRRRR

456231

R +=

654

456

111

RRR

R ++=

−



, T

123 4

Figure IVa.5.4. A composite wall, which consists of stacked conductors arranged in series