Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


472 IVa. Heat Transfer: Conduction
The next example deals with temperature distribution in an annular fuel rod
with two-stream coolant and inner as well as outer cladding. In this example, we
have assumed no contact resistance hence, no gap exists between the fuel and both
inner and outer cladding.
Example IVa.6.3. Find the maximum temperature and its location in a two-
stream annular fuel rod with inner and outer cladding. Data: T
i
= 325 C, T
o
= 300
C, h
i
= 6000 W/m
2
·C, h
o
= 4500 W/m
2
·C, k
F
= 3.5 W/m·C, k
C
= 11 W/m C, q
′
=
10 kW/ft, d
1
= 0.6 cm, d
2
= 0.8 cm, d
3
= 1.4 cm, and d
4
= 1.6 cm.
Clad
Fuel
Coolant
T
i
T
1
T
2
T
3
T
4
T
o
d
1
d
2
d
3
d
4
r
T
i
T
o
T
4
T
3
T
2
T
1
Solution: This is a one-dimensional, steady state problem with heat generation in
a two-stream annular fuel rod, having constant thermal conductivity and negligible
contact resistance. Solution for temperature distribution in the inner cladding (i.e.,
for the region between r
1
to r
2
) is found from Equation IVa.6.10:
21
ln crcT
C
+=
21
rrr ≤≤
Similarly, Equation IVa.6.10 is the solution to temperature distribution in the fuel
region:
43
2
)ln()4/( crcrkqT
FF
++
′′′
−=
32
rrr ≤≤
Finally, temperature distribution in the outer clad region (i.e., for the region be-
tween r
3
and r
4
) is given by:
65
ln crcT
C
+=
43
rrr ≤≤
There are 6 coefficients, which can be found from the following 6 boundary con-
ditions:
Location Boundary Condition Location Boundary Condition
r = r
1
k
C
dT
C
/dr = h
i
(T
C
– T
i
) r = r
3
T
F
= T
C
r = r
2
T
C
= T
F
r = r
3
–k
F
dT
F
/dr = –k
C
dT
C
/dr
r = r
2
–k
C
dT
C
/dr = –k
F
dT
F
/dr r = r
4
–k
C
dT
C
/dr = h
o
(T
C
–
T
o
)
Upon substitution we find;

6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 473
¸
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
¨
©
§
′′′
′′′
′′′
−
′′′
−
=
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
+
−
−−
−
−−
−
oo
F
F
ii
oCo
CF
FC
iCi
Th
rq
krq
rq
krq
Th
c
c
c
c
c
c
hrkrh
rkrk
rr
rkrk
rr
hrkrh
2/
4/
2/
4/
/ln0000
0/1/00
1ln1ln00
000/0/
001ln1ln
0000/ln
3
2
3
2
2
2
6
5
4
3
2
1
44
33
33
22
22
11
Since r
1
= 0.3 cm, r
2
= 0.4 cm, r
3
= 0.7 cm, r
4
= 0.8 cm, and qqrr
′
=
′′′
−
)(
2
2
2
3
π
then
()
8E165.3
/cm4m-1Ecm4.07.0
ft/m2802.3)W/kW1000kW/ft10(
)(
222222
2
2
3
=
×−
××
=
−
′
=
′′′
ππ
rr
q
q
W/m
3
=
316.5 MW/m
3
Substituting numerical values, the above matrix equation becomes:
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
−
−
=
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
©
§
−
−
−−
−
−−
−
7E1350.0
7.110760E0
4E110760.0
6E63294.0
3E36167.0
7E1950.0
45004.203520000
043.1571150000
19618.419618.400
00087502750
001521.51521.5
000060005.38521
6
5
4
3
2
1
c
c
c
c
c
c
Thus, c
1
= 213.84, c
2
= 1697.94, c
3
= 1395.44, c
4
= 8443.67, c
5
= –255.46, and c
6
= –855.37
Location of the maximum temperature is found from:
r(T
max
) = qkc
F
′′′
/2
3
and the maximum temperature itself is obtained from:
T
max
= –22.6r
2
+ c
3
ln[r(T
max
)] + c
4
Substituting values, we find r(T
max
) = 0.556 cm and T
max
= 1894.6 C.
6.4. 1-D S-S Heat Conduction in Solid Cylinders ( )(Tfq =
′′′
)
If we can express
Tccq
21
+=
′′′
then Equation IVa.2.8 for steady state conditions
can be written as:
0'
'1'
2
2
2
=++ TB
dr
dT
r
dr
Td
IVa.6.19
474 IVa. Heat Transfer: Conduction
Where B
2
= c
2
/k
f
. Equation IVa.6.19 is a Bessel differential equation having the
solution of:
)()()('
0201
BrYABrJArT +=
Where J
0
and Y
0
are zero order Bessel functions of first and second kind, respec-
tively. From symmetry we conclude that A
2
= 0 as Y
0
approaches infinity and r
approaches zero. A
1
can be found from the boundary condition at the surface.
Bessel functions are discussed in Section 3 of Chapter VIIb.
7. Analytical Solution of 1-D S-S Heat Conduction Equation, Sphere
We seek temperature distribution only in the radial direction due to the symmetry
in the
φ
and
θ
directions. If such symmetry does not exit, we must find a multi-
dimensional solution.
We consider several cases for steady state heat transfer in a sphere. These in-
clude temperature profile in hollow spheres with no heat generation, heat loss
from insulated spheres, and temperature profile in solid and hollow spheres with-
out and with volumetric heat generation.
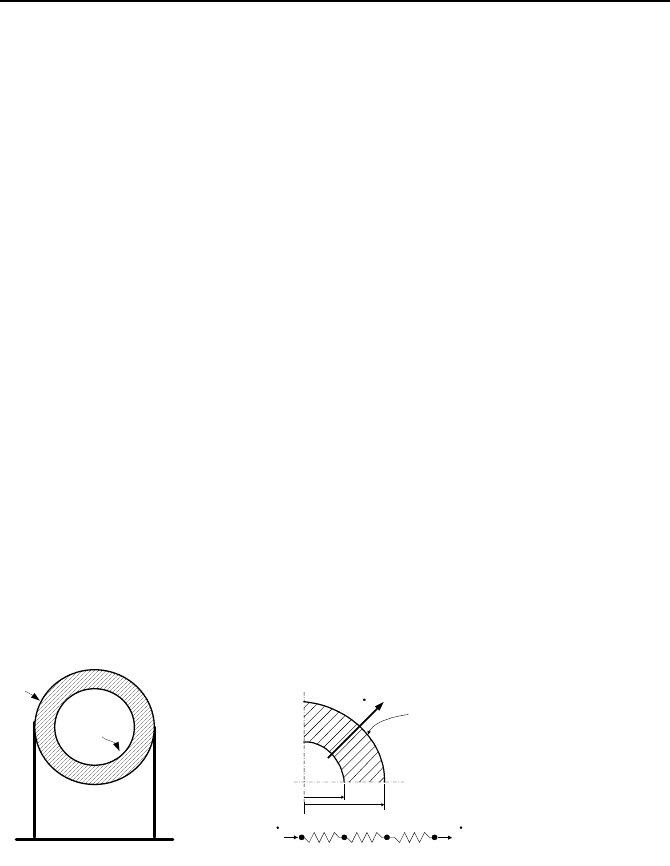
7.1. 1-D S-S Heat Conduction in Hollow Spheres (
0=
′′′
q
)
A spherical container holds a liquid at constant temperature (Figure IVa.7.1). We
assume that the liquid is warmer than ambient and the heat loss is steadily sup-
plemented by an electric heater, heating the liquid.
T
fb
, h
b
T
fa
, h
a
T
f2
r
1
r
2
T
2
T
1
T
f1
T
f2
, h
2
T
f1
, h
1
R
3
R
2
R
1
Q
Q
Q
Figure IVa.7.1. Heat conduction in a hollow sphere
The resistances represent the internal convection, conduction through the
sphere wall, and the external convection, respectively. To obtain thermal resis-
tance of the sphere wall, we note that the same amount of heat passes through all
the wall layers. Since the surface area of a layer at radius r is 4
π
r
2
:
drdTrkdrkAdTQ /)4(/
2
π
−=−=
7. Analytical Solution of 1-D S-S Heat Conduction Equation, Sphere 475
We may now rearrange this equation to obtain:
dT =
Q
dr/(4
π
kr
2
)
Integrating between T(r = r
1
) = T
1
and T(r = r
2
) = T
2
results in:
∆T = Q
(1/r
1
– 1/r
2
)/4
π
k = q
R
where the sphere thermal resistance is given as R
Sphere
= (1/r
1
– 1/r
2
)/4πk.
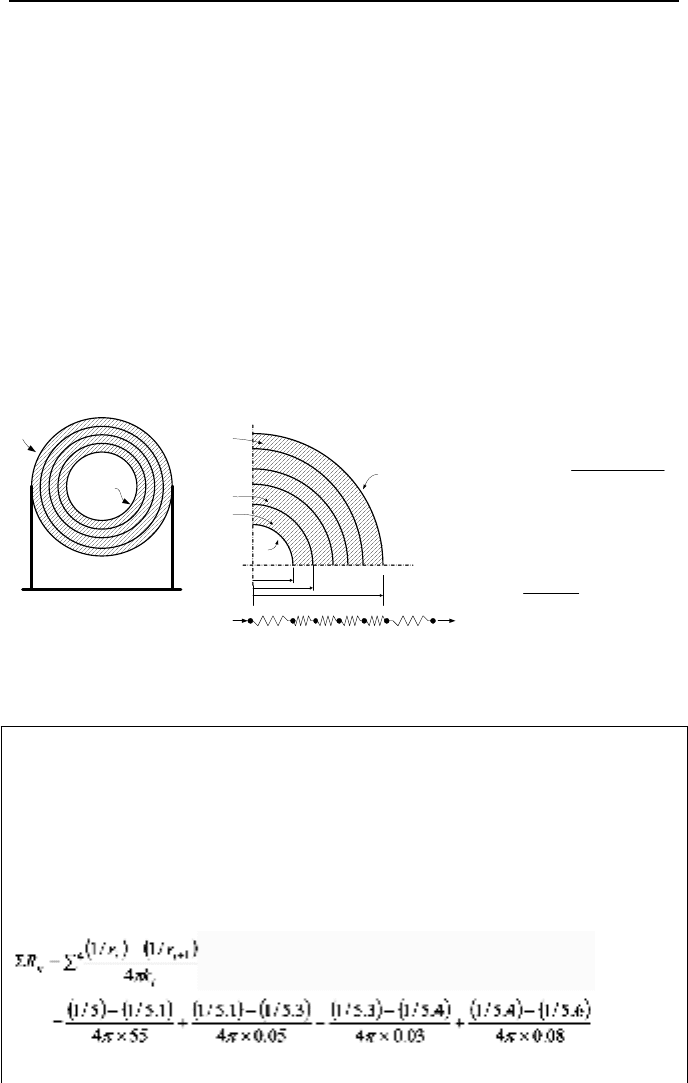
Steady State Heat Loss from Insulated Spheres
We may extend the above result to find thermal resistance of a spherical wall and
layers of insulation. These thermal resistances are summarized in Figure IVa.7.2.
T
fb
, h
b
T
fa
, h
a
T
fb
r
1
r
2
r
n
T
2
T
1
T
fa
T
n
T
fb
, h
b
R
b
R
n
R
1
R
a
k
2
k
1
Q
.
k
n
T
fa
, h
a
....
Q
.
....
()( )
¦¦
−
=
−
=
+
1
1
1
4
/1/1
n
i
i
ii
n
k
rr
R
π
bna
RRRR +
¦¦
+=
aaa
AhR /1=
bbb
AhR /1=
¦
−
=
R
TT
Q
fbfa
Figure IVa.7.2. Electric resistance analogy for heat conduction in spheres with multiple
layers of insulation
Example IVa.7.1. Liquid at 180 C is stored in a steel spherical container, which
is covered with three layers of insulation. Find the rate of heat loss. Data: r
1
= 5
m, r
2
= 5.1 m, r
3
= 5.3 m, r
4
= 5.4 m, r
5
= 5.6 m, h
a
= 500 W/m
2
·C, h
b
=
100 W/m
2
·C, T
fb
= 35 C, k
Carbon Steel
= 55 W/m·C, k
1
= 0.05 W/m·C, k
2
= 0.03
W/m·C, k
3
= 0.08 W/m·C.
Solution: We find thermal resistances as follows:
Inside sphere: R
a
= 1/[(
π
2
1
r )h
a
] = 1/[(
π
× 5
2
) × 500] = 2.55E-5 C/W
ΣR
n
= 5.67E-6 + 0.118 + 9.27E-3 + 6.58E-3 = 0.134 C/W

476 IVa. Heat Transfer: Conduction
Outside sphere: R
b
= 1/[(
π
2
5
r )h
b
] = 1/[(
π
× 5.6
2
) × 100) = 1E-4 C/W
ΣR = 2.55E-5 + 0.134 + 1E-4 ≅ 0.134 C/W
Rate of heat transfer: Q
= (T
fa
– T
fb
)/ΣR = (180 – 35)/0.134 = 1.08 kW.
To find the temperature distribution in the wall of a bare hollow sphere without
internal heat generation, we use Equation IVa.2.10 and retain only the first term in
the left side of the equation:
0
1
2
2
=
¸
¹
·
¨
©
§
dr
dT
r
dr
d
r
When integrated we get r
2
dT/dr = c
1
or alternatively, dT/dr = c
1
/r
2
. Integration of
this equation gives:
T = –c
1
/r + c
2
r IVa.7.1
Coefficients c
1
and c
2
are found from a specified set of boundary condition. For a
convection boundary of T
fa
and h
a
for the inside (r = r
a
) and T
fb
and h
b
for the out-
side (r = r
b
) of the sphere we write:
()
[]
a
a
rr
rr
faa
dr
dT
kTTh
=
=
¸
¹
·
¨
©
§
−=− and
()
[]
fb
rr
b
rr
TTh
dr
dT
k
b
b
−=
¸
¹
·
¨
©
§
−
=
=
where we assumed that T
fa
> T
fb
. Upon substitution of Equation IVa.7.1 in the
above boundary conditions, coefficients c
1
and c
2
are calculated and temperature
profile in the sphere wall is obtained.
7.2. 1-D S-S Heat Conduction in Solid Spheres (
0≠
′′′
q
)
An example of one-dimensional heat conduction in spheres with internal heat gen-
eration is the fuel balls in a gas cooled nuclear reactor. Fission heat is generated
inside the fuel ball and removed at the surface by the coolant. Temperature distri-
bution in spherical fuels is the solution to Equation IVa.2.10 at steady state;
0)(
1
2
2
=
′′′
+
∂
∂
∂
∂
k
q
r
T
r
r
r
This equation can be easily integrated to obtain T = –( q
′′′
/6k)r
2
+ c
1
/r + c
2
and,
recognizing that at r = 0 temperature is finite, c
1
= 0. We obtain c
2
from an appro-
priate boundary condition.
Example IVa.7.2. Temperature at the center of a spherical fuel element is 2000
C. Find the surface temperature. Data: d = 1 cm, k
F
= 3.5 W/m
2
·C, and q
′′′
= 630
MW/m
3
.

8. Analytical Solution of Heat Conduction Equation, Extended Surfaces 477
Solution: At r = 0 m, T = 2000 C hence, c
2
= 2000 C. The profile becomes:
T = –( q
′′′
/6k)r
2
+ 2000
We now find temperature at r = 0.5/100 m, T = –[630E6/(6 × 3.5) × (5E-3)
2
+
2000 = 1250 C.
7.3. 1-D S-S Heat Conduction in Spheres ( 0≠
′′′
q
)
For spherical fuel pellets where
Tccq
21
+=
′′′
, the Helmholtz equation becomes:
0'
'2'
2
2
2
=++ TB
dr
dT
r
dr
Td
IVa.7.2
where
B
2
= c
2
/k
f
. The solution to this linear second-order differential equation
is:
Br
Br
A
Br
Br
AT
)sin()cos(
'
21
+=
where coefficients A
1
and A
2
can be found from the boundary conditions. From
symmetry we conclude that A
2
= 0. Having A
2
, we can find A
1
from the boundary
conditions specified at the surface.
8. Analytical Solution of Heat Conduction Equation,
Extended Surfaces
In Section IVa.3 we studied surfaces covered with multiple layers of insulation
used to reduce the rate of heat transfer. In this section, we will study means of en-
hancing the rate of heat transfer, which is accomplished by the use of extended
heat transfer surfaces or fins. There is a variety of designs for fins that can be
categorized in three classes: longitudinal, circular, and spine. Each class has its
own variety of designs depending on the fin profile. Figure IVa.8.1 shows four
profiles of longitudinal fins.
Figure IVa.8.1. Longitudinal fins of rectangular, triangular, trapezoidal, and parabolic pro-
files

478 IVa. Heat Transfer: Conduction
The purpose of fin thermal analysis is to determine temperature gradient in the
fin and the rate of heat transfer from the fin. We begin with the analysis of a lon-
gitudinal fin with variable area as shown in Figure IVa.8.2. In the derivation that
follows, we assume that the fin is made of homogeneous material with constant
thermal conductivity. We will also assume that the conduction-convection ar-
rangement guarantees a low Biot number so that heat transfer can be treated pri-
marily as one-dimensional. Additionally, the heat transfer coefficient and tem-
perature of the convection boundary are assumed constant.
8.1. 1-D S-S Heat Conduction in Fins (
0=
′′′
q
)
To be able to analyze fins using the one-dimensional heat conduction equation, we
assume that both sides of the fin (parallel to the
xy-plane) are insulated, or L >> l.
Since the direction of heat transfer is perpendicular to the shaded and the cross-
hatched areas and these areas change as a function of
x, we need to write the con-
servation equation of energy for the elemental control volume shown in the right
side of Figure IVa.8.2. At steady state, the rate of energy leaving the top area by
convection, the front area by conduction, and the bottom area by convection is
equal to the rate of energy entering from the rear (shaded) area by conduction:
)()(
f
x
xx
TThdSdx
dx
Qd
QQ −++=
2
δ
L
dx
h , T
f
x
y
l
y=f(x)
h(Ldx)(T - T
f
)
h(Ldx)(T - T
f
)
Q
x
.
Q
x
+(dQ
x
/ dx)dx
.
.
Figure IVa.8.2. Longitudinal fin with variable cross-sectional area
Two observations must be made at this point. First, we represented the whole
control volume by only one temperature. Second, the surface area for convection
heat transfer of the control volume (dA) is equal to the perimeter times the width
of the control volume (i.e., dS = 2(L + y)dx = Pdx where P = 2(L + y) is the con-
trol volume perimeter). We now introduce an approximation by ignoring y com-
pared with L. The control volume perimeter is, therefore, approximated as
L
2P ≅ . In other words, we have ignored heat transfer from the sides of the fin to
be consistent with 1-D assumption. After substitution and simplification we find:
0)(P =−+
f
x
TTh
dx
Qd
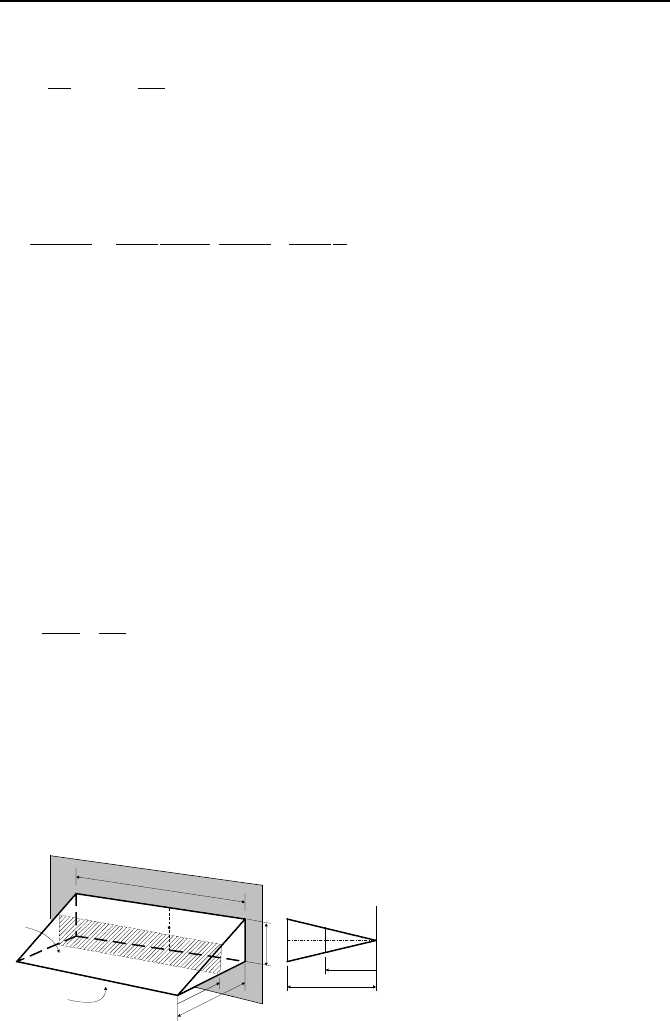
8. Analytical Solution of Heat Conduction Equation, Extended Surfaces 479
We may now substitute for the rate of heat transfer from Fourier’s law:
0)(P])([ =−+−
f
TTh
dx
dT
xkA
dx
d
Carrying out the derivative term and representing
θ
=−
f
TT , where dT/dx =
d
θ
/dx, we obtain:
0)(
)(
P)(
]
)(
)(
1
[
)(
2
2
=−+ x
k
h
xAdx
xd
dx
xdA
xA
dx
xd
θ
θθ
IVa.8.1
Temperature profile in the fin is the solution to Equation IVa.8.1. To find the rate
of heat transfer from the fin, we use Fourier’s law and calculate the temperature
derivative at the base. That is to say that the total rate of heat transfer from the fin
to the convection boundary must be supplied from the base. Finding an analytical
solution for this differential equation depends on the degree of complexity of the
function y = f(x) of Figure IVa.8.2, the fin heat transfer area profile. Solution for a
linear profile is discussed next.
Case 1. Longitudinal Fins with Triangular Profile. Shown in Figure IVa.8.3 is a
fin with triangular profile. For this linear profile, y is expressed in terms of x as y
= (b/l)x. The area for heat diffusion at x becomes A = (bL/l)x, and term Ph =
L(h
1
+h
2
). Note that x is measured from the tip of the fin. Upon substitution, the
differential equation for temperature distribution in the fin becomes:
0
2
2
2
=−+
θ
θθ
m
dx
d
dx
d
x
IVa.8.2
Where m
2
= (h
1
+h
2
)L/bk. Equation IVa.8.2 is a Bessel differential equation hav-
ing a solution of:
)2()2()(
2/1
02
2/1
01
mxKcmxIcx +=
θ
L
x
b
l
h
1
, T
f1
h
2
, T
f2
l
x
T = T
0
y
y
Figure IVa.8.3. Steady state temperature distribution in longitudinal fins with triangular
profile

480 IVa. Heat Transfer: Conduction
Where I
0
and K
0
are order-zero modified Bessel functions of the first and sec-
ond kind, respectively. To find coefficients c
1
and c
2
, we use two boundary condi-
tions. The first boundary condition deals with temperature at x = 0 which must be
finite. However, as Figure VIIb.3.1 shows, K
0
approaches infinity as x approaches
zero. Since temperature is finite, this implies that c
2
must be set equal to zero c
2
=
0. The second boundary condition is at x = l (i.e. T(l) =T
b
where subscript b
stands for base). Since
f
TT −=
θ
, then
f
TT −=
00
θ
. Substituting, we find
)2(/
2/1
001
mlIc
θ
= . Temperature profile in the fin then becomes:
)2(
)2(
2/1
0
2/1
0
0
mlI
mxI
TT
TT
f
f
=
−
−
The rate of heat transfer from the entire fin is equal to the rate of heat diffusion at
the base given by
dxdTkAQ
bfin
/−=
. Upon substitution, we obtain:
)2(
)2(
/))((
2/1
0
2/1
1
2/1
0
mlI
mlI
ml
lTTbLk
Q
f
fin
=
−
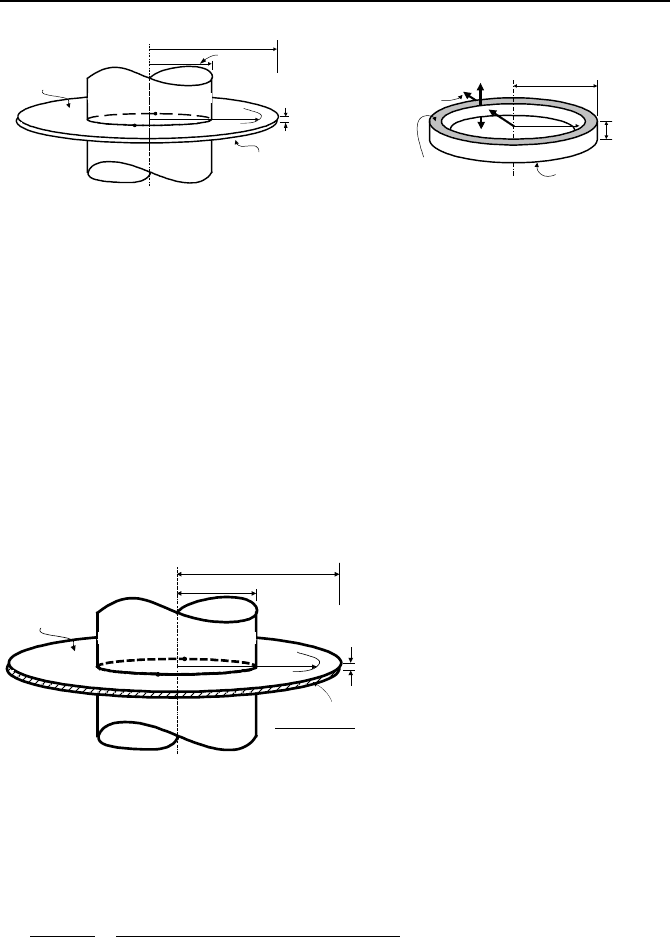
Case 2: Annular Fins with Rectangular Profile. Annular fins, as shown in
Figure IVa.8.4, are another example of fins with a variable heat conduction area.
We may derive the governing equation similar to Case 1 or use the result obtained
for Case 1 in Equation IVa.8.1. The reader may perform the derivation by taking
advantage of the energy balance in the elemental control volume of Figure IVa.8.4
and note that the rate of thermal energy steadily provided by the base, at radius
r
b
and temperature of T
b
, is dissipated by convection to the environment by the fin.
To use Equation IVa.8.1, the perimeter is found as P = 2(2
π
r) and the heat con-
duction area as A(r) =(2
π
r)(2
δ
). Thus the governing equation becomes:
0
1
2
2
2
=−+
θ
θθ
m
dr
d
r
dr
d
IVa.8.3
where
δ
khm /
2
= . Equation IVa.8.3 is a Bessel differential equation with the
following solution:
)()()(
0201
mrKcmrIcTrT
f
+=−
8. Analytical Solution of Heat Conduction Equation, Extended Surfaces 481
r
b
r
t
r
2
δ
h , T
f
h , T
f
T
b
2
δ
h , T
f
r
r+dr
h , T
f
h(Pdr)(T- T
f
)
Q
.
Q + (dQ/dr)dr
..
Figure IVa.8.4. Schematic of an annular fin with rectangular profile
To find the coefficients we use the boundary conditions at the base and at the
tip of the fin. Temperature of the base, T
b
is generally specified so that T(r
b
) = T
b
.
For the second boundary condition, we should use the convection boundary condi-
tion at r = r
t
over the surface area of S = 2
π
r
t
(2
δ
). However, a mathematically
simpler means to accomplish this is to have an insulated boundary at the tip and
add the surface area to the top and the bottom of the fin. This is acceptable if the
heat transfer coefficient for the vertical surface is the same as for the horizontal
surfaces. By adding the vertical surface area to the horizontal area, the new fin di-
ameter becomes r
t
+
δ
and the second boundary condition at r’ = r
t
+
δ
can be
written as dT/dr = 0.
r
b
r
t
+
δ
r
2
δ
h , T
f
T
b
dT(r
t
+
δ
)
dr
= 0
r' =
Figure IVa.8.5. Annular fin with insulated tip
We use these boundary conditions to find coefficients c
1
and c
2
. Upon substitu-
tion, the temperature profile in the fin is found as :
)()'()'()(
)()'()()'(
0110
0101
bbfb
f
mrKmrImrKmrI
mrImrKmrKmrI
TT
TT
+
+
=
−
−
IVa.8.4
where I and K are the modified Bessel functions of the first and second kind.
Some Bessel functions for 0 < x < 4 are given in Table VIIb.3.1. The rate of heat
transfer can then be calculated from:
