Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


452 IVa. Heat Transfer: Conduction
Example IVa.5.4. The wall of a containment building consists of 6 mm steel
liner and 50 cm concrete. The steel liner facing the interior is coated with 2 mm
of primer and 3 mm of paint. The outside of the concrete is coated with 3 mm
paint. Find the heat loss through the wall, treated as a slab. Ignore contact resis-
tance.
Data: T
a
= 127 C, T
b
= 27 C, k
concrete
= 3.5 W/m·C, k
steel
= 60 W/m·C, k
paint
= 0.5
W/m·C, k
primer
= 1.7 W/m·C, h
a
= 120 W/m
2
·C, and h
b
= 25 W/m
2
·C.
Solution: We first calculate thermal resistances per unit surface area (1 m
2
) of the
wall from inside to outside:
R
a
= 1/(h
a
A) = 1/(120 × 1) = 8.3E-3 C/W
R
paint
= ∆x
paint
/(k
paint
A) = 3E-3/(0.5 × 1) = 6E-3 C/W
R
primer
= ∆x
primer
/(k
primer
A) = 2E-3/(1.7 × 1) = 1.2E-3 C/W
R
steel
= ∆x
Steel
/(k
steel
A) = 6E-3/(60 × 1) = 1E-4 C/W
R
concrete
= ∆x
Concrete
/(k
Concrete
A) = 0.50/(3.5 × 1) = 0.14 C/W,
R
paint
= ∆x
paint
/(k
paint
A) = 3E-3/(0.5 × 1) = 6E-3 C/W
R
b
= 1/(h
b
A) = 1/(25 × 1) = 0.04 C/W
Thus, ΣR = 8.3E-3 + 6E-3 + 1.2E-3 + 1E-4 + 0.14 + 6E-3 + 0.04 = 0.2016 C/W
Therefore, we find (127 27) / 0.2016 496q =− =
′′
W/m
2
. The rate of heat loss
without any paint and primer increases by 7%.
5.2. 1-D S-S Heat Conduction in Slabs ( 0≠
′′′
q
)
A slab with internal heat generation is shown in Figure IVa.5.5. The goal is to
find the steady state (
0/ =∂∂ tT ) temperature distribution in the slab, assuming
constant thermal conductivity (
0/ =∂∂ Tk ). Equation IVa.2.4 simplifies to:
0
)(
1)(
2
2
=
∂
∂
=
′′′
+
∂
∂
t
xT
k
q
x
xT
α
IVa.5.5
For a uniform volumetric heat generation rate, Equation IVa.5.5 can be integrated to obtain:
2L
x
h , T
f
h , T
f
T(x)
q'''
.
Figure IVa.5.5. Slab with internal heat generation
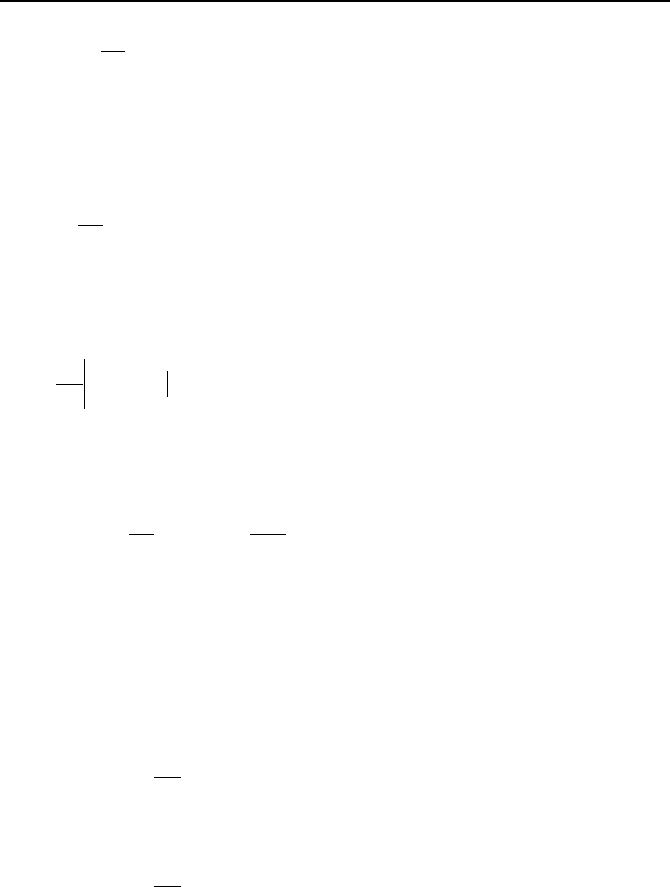
5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 453
21
2
2
)( cxcx
k
q
xT ++
′′′
−=
IVa.5.6
where constants c
1
and c
2
can be determined from a set of boundary conditions.
Since a convection boundary condition of h, T
f
is specified for both sides of the
slab, we can find the constants by taking advantage of the fact that the center plane
is adiabatic due to symmetry –kdT/dx(0) = 0:
()
02
2
0
1
=
»
¼
º
«
¬
ª
+
′′′
−−
=x
cx
k
q
k
resulting c
1
= 0. This also implies that the center plane has the maximum tempera-
ture. We now use the second boundary condition, which specifies that the heat
transfer by conduction at x = L is removed by convection:
0)( =−−−
=
=
f
Lx
Lx
TTh
dx
dT
k
Substituting for T(L), from Equation IVa.5.6, we find coefficient c
2
as
f
TkLqhLqc +
′′′
+
′′′
= )2/()/(
2
2
. Thus, the profile is:
h
Lq
xL
k
q
TxT
f
′′′
+−
′′′
+=
)(
2
)(
22
IVa.5.7
Having the temperature profile for the slab with internal heat generation, we can
find temperature of the center plane (i.e., at x = 0):
)/2/()0(
2
max
hLkLqTTxT
f
+
′′′
+===
If we substitute for T
f
in Equation IVa.5.7 we find the temperature profile in terms
of T
max
:
2
max
2
)( x
k
q
TxT
′′′
−=
IVa.5.8
The surface temperature can be found by setting x = L:
2
max
2
)( L
k
q
TLT
′′′
−=
IVa.5.9
The rate of heat transfer from each surface is equal to the rate of volumetric heat
generation rate in half of the slab volume (i.e.,
qQ
′′′
=
× AL) where A is the heat
transfer area of the slab. If we substitute for
q
′′′
from the Equation IVa.5.9 we get
)/(2 LTkQ ∆=
. This is twice the rate of heat transfer from an identical slab but
with no internal heat generation.
454 IVa. Heat Transfer: Conduction
5.3. 1-D S-S Heat Conduction in Composite Slabs ( 0≠
′′′
q
)
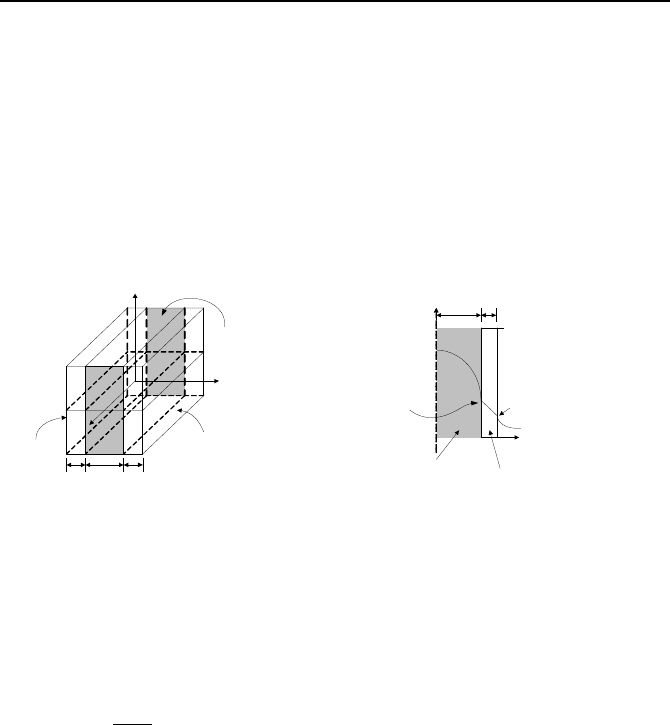
If the slab with internal heat generation is made of fissile materials (referred to as
fuel), sheath or cladding is used to contain the by-products of nuclear fission.
Suppose the thickness of the slab representing the fuel material is 2L and the
thickness of slab representing each cladding is
δ
. The goal is to find the steady
state (
∂T/∂t = 0) temperature distribution in the slab assuming constant thermal
conductivity (
∂k/∂T = 0) for both fuel and cladding but with internal heat genera-
tion (
0≠
′′′
q
) produced uniformly only in the inner slab (fuel) as shown in Fig-
ure IVa.5.6.
T
F1
T
C2
Fuel
Cladding
δ
L
x
y
T
f
T
C1
T
F2
h, T
f
=
z
y
x
2L
δδ
Fuel
Cladding
h, T
f
h, T
f
Cladding
q
′′′
Figure IVa.5.6. Slab with internal heat generation and cladding
This is a two-region problem. For a specified convection boundary condition,
we can determine the temperature profile and the rate of heat transfer by solving
the heat conduction equation in the fuel region (shown by subscript F) and in the
clad region (shown by subscript C). Due to symmetry, we only consider half of
the composite slab. For the fuel region Equation IVa.5.6 is applicable:
21
2
2
)( cxcx
k
q
xT
F
F
++
′′′
−=
, Lx ≤≤0
For the clad region, where
δ
+≤≤ LxL with
δ
being the clad thickness, Equa-
tion IVa.5.1 is applicable so that d
2
T
C
/dx
2
= 0 resulting in
43
)()( cLxcxT
C
+−=
where we assumed that no heat is generated in the cladding. Since there are four
unknowns (c
1
, c
2
, c
3
, and c
4
) we need four boundary conditions. One boundary
condition takes advantage of symmetry and sets heat transfer at the adiabatic yz-
plane to zero. The second boundary condition takes into account heat transfer by
convection at x = L + d. The third and the fourth boundary conditions deal with
equal temperature and equal heat flux at the boundary between the two regions of
fuel and cladding, assuming no contact resistance.
From the first boundary condition we find that c
1
= 0. Using the second
boundary condition we write:

5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 455
0])([
)(
=−+=−
∂
+=∂
−
fC
C
C
TcLxTh
x
cLxT
k
From the third boundary condition (i.e., equal temperatures at the common sur-
face) we get:
421
2
)(
2
)( cLxTcLcL
k
q
LxT
C
F
F
+==++
′′′
−==
Finally from the fourth boundary condition (i.e., equal heat flux at the common
surface) we obtain:
0]
)(
[
)(
=
∂
∂
−−
∂
∂
−
x
LT
k
x
LT
k
C
C
F
F
Solving for c
1
through c
4
, the temperature profile for the fuel region, in dimen-
sionless terms, becomes:
Lx
Lh
k
Lk
k
L
x
kLq
TxT
C
C
F
F
fF
≤≤
»
¼
º
«
¬
ª
++
¸
¹
·
¨
©
§
−=
′′′
−
021
2/
)(
2
2
δ
and for the cladding region:
cLxL
Lh
k
LL
x
kLq
TxT
C
C
fC
+≤≤
»
¼
º
«
¬
ª
++
¸
¹
·
¨
©
§
−=
′′′
−
δ
1
/
)(
2
Note that we neglected contact resistance and assumed that thermal conductivity
of the fuel region is independent of temperature. For nuclear fuels, such as ura-
nium, these are not accurate assumptions.
5.4. 1-D S-S Heat Conduction in Slabs (
)(Tfq =
′′′
)
So far we dealt with a uniform internal heat generation rate that remained constant
regardless of the fuel temperature. However, due to a phenomenon known as the
Doppler effect, as fuel temperature increases, there is a mechanism known as the
negative reactivity coefficient, which tends to reduce the rate of fission and
thereby the rate of heat generation. A simple way to account for the dependency
of the internal heat generation rate on temperature is to assume a linear function so
that
Tccq
21
+=
′′′
where c
1
and c
2
are known constants. By substituting this rela-
tion in Equation IVa.2.4, we obtain the Poisson equation:
0
21
2
=
+
+∇
F
k
Tcc
T
IVa.5.10
We can transform Equation IVa.5.10 to a Helmholtz equation by introducing a
linear transformation as:
456 IVa. Heat Transfer: Conduction
)/(
21
ccTT +=
′
IVa.5.11
Upon substitution of Equation IVa.5.11 in Equation IVa.5.10, we get:
0''
2
2
=+∇ T
k
c
T
F
IVa.5.12
For the slab in Figure IVa.5.5, the equation becomes d
2
T’/dx
2
+ B
2
T ’ = 0 where B
2
= c
2
/k
F
. This is a second order linear differential equation. Since B
2
is positive,
the answer is a trigonometric function (Chapter VIIa):
)cos()sin()('
21
BxABxAxT +=
where coefficients A
1
and A
2
can be found from specified boundary conditions.
For example, for the conditions of Figure IVa.5.5, A
1
must be zero due to symme-
try hence, T’(x) = A
2
cos(Bx). Finding A
2
from the convection boundary, the tem-
perature profile for a slab fuel with a temperature-dependent heat generation rate
becomes:
)cos(
)sin()cos(
)(' Bx
BLBkBLh
hT
xT
F
f
−
=
Example IVa.5.5. Find temperature at x = L/2 for a plate-type fuel.
Data: c
1
= –0.01 kW/m
3
, c
2
= 125 kW/m
3
·C, k
F
= 2 W/m·C, T
f
= 288 C,
h = 8 kW/m
2
·C, 2L = 0.6 cm.
Solution: Using the data, we first find the argument BL:
B = (c
2
/k
F
)
1/2
= (125/2)
1/2
= 7.9 m
-1
. Thus BL = 7.9 × 0.003 = 0.237
)(' xT =
)9.7cos(296)9.7cos(
)237.0sin(002.09.7)237.0cos(8
2888
xx =
×−
×
T’
L/2
≅ 296cos(0.237) ū 294 C. We find T
L/2
= T’
L/2
– (c
1
/c
2
) ū 294 C.
5.5. Bombardment of Slabs with Energetic Radiation ( )(xfq =
′′′
)
We now discuss an interesting conduction problem where the volumetric heat
generation rate is a function of location. This occurs when materials are exposed
to high-energy radiation. Consider exposure of a cold iron plate to solar radiation.
Temperature penetration in the plate is a function of the radiation intensity at the
plate surface exposed to radiation. Mathematically, this affects the solution via
boundary condition at the exposed surface. By contrast, if the same plate is ex-
posed to neutron or gamma radiation, the energetic beam penetrates deep into the
plate, interacting with the iron atoms, and depositing energy in each interaction.
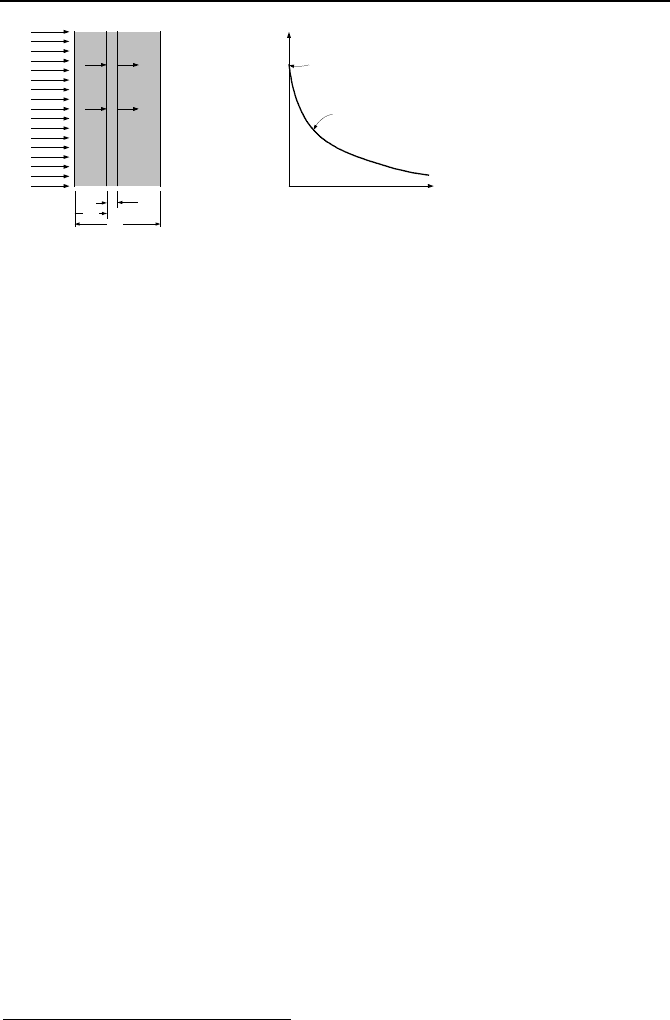
5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 457
L
x
dx
x
q
dxx
q
+
x
q
′′′
0
q
′′′
x
eqxq
µ
−
′′′
=
′′′
0
)(
φ
x
φ
x+dx
φ
0
Figure IVa.5.7. Bombardment of a slab by high-energy radiation
The interaction of the high-energy radiation with the atoms of the medium at-
tenuates the radiation intensity. Since the rate of interaction at any location in the
medium is directly proportional to the number of particles in that location, it can
be easily shown that the rate of interaction decreases exponentially. To demon-
strate, let’s say that
φ
represents the number of particles of the high energy radia-
tion that have penetrated the medium to depth x per unit time and per unit surface
area of the medium. We call this quantity, flux. If the particles are photons,
φ
represents the flux of gamma radiation and if the particles are neutrons,
φ
is neu-
tron flux. We now consider the elemental control volume located at x and ex-
tended to dx. Particles that enter this control volume interact with the atoms of the
material comprising the control volume. Since in each interaction a particle is re-
moved, the number of particles leaving this control volume (at x + dx) has de-
creased by
φ
lost
. A particle balance yields
φ
x
=
φ
x+dx
+
φ
lost
. To find the rate of par-
ticles which have had interaction (i.e., dropped out
φ
lost
) we introduce the
absorption coefficient,
µ
. This coefficient represents the likelihood that a particle
would have an interaction with an atom of the medium per unit distance of travel
in the medium. Hence, in traveling dx, there is a chance equal to
φ
(
µ
dx) that a
particle would have an interaction in the medium. Substituting for
φ
lost
=
φ
(
µ
dx)
and for
φ
x+dx
≅
φ
x
+ (d
φ
x
/dx)dx in the particle balance, we find:
φ
x
= [
φ
x
+ (d
φ
x
/dx)dx] +
φ
x
(
µ
dx) IVa.5.13
Equation IVa.5.13 simplifies to d
φ
/dx = –
µφ
. Upon integration from x = 0 where
particle flux is
φ
o
to any x, the radiation flux in the medium is obtained as:
φ
(x) =
φ
o
e
–
µ
x
IVa.5.14
The absorption coefficient (
µ
) introduced above is the probability of interaction
per unit distance of travel. This is usually expressed in cm
–1
. Values of
µ
for vari-
ous shielding materials are given in Table A.V.1(SI)
*
.
*
The type of interaction of the incident radiation with the atoms of the medium depends on
the nature and the energy of the incident radiation as well as the material of the medium.
If the radiation consists of neutrons, then the type of interaction may be absorption or scat-
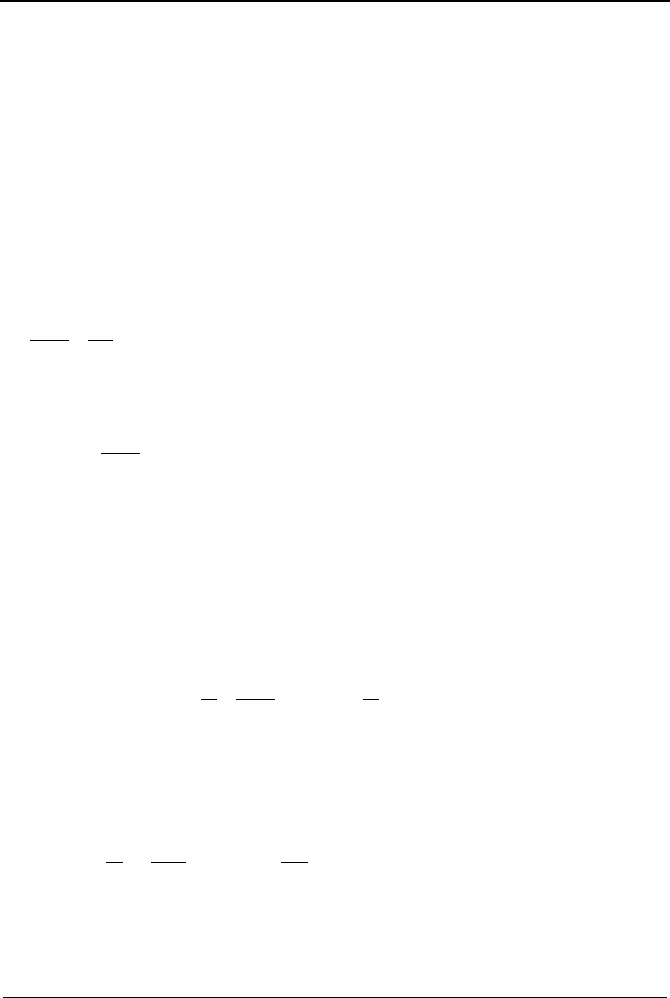
458 IVa. Heat Transfer: Conduction
If ∆E is the energy transferred to the atoms of the medium in each collision,
then the rate of energy transfer is given as I =
φ
∆E where I has the units of energy
per unit time and unit surface area. Hence, the amount of heat generated in the
medium per unit volume is
Iq
µ
=
′′′
, having the units of energy per unit time and
unit volume. Substituting for I in terms of flux from Equation IVa.5.14, for
gamma bombardment we obtain:
x
eqxq
µ
−
′′′
=
′′′
0
)(
IVa.5.15
The governing equation for heat conduction can either be derived from an energy
balance using the control volume of Figure IVa.5.7 or obtained from the simpli-
fied form of Equation IVa.2.4:
0
0
2
2
=
′′′
+
− x
e
k
q
dx
Td
µ
IVa.5.16
Equation IVa.5.16 has an analytical solution. Integrating this equation twice,
yields:
21
2
0
)( cxce
k
q
xT
x
++
′′′
−=
−
µ
µ
IVa.5.17
where constants c
1
and c
2
in Equation IVa.5.17 are found from a specified set of
boundary conditions. We shall consider two types of boundary conditions; speci-
fied surface temperature and specified heat convection.
Case 1. Specified Surface Temperature: If the surface temperatures are specified
at T(x = 0) = T
0
and T(x = L) = T
L
as boundary conditions, we can then find the so-
lution as:
()()
»
¼
º
«
¬
ª
−−−
′′′
+−+=
−−
11)()(
2
0
00
xL
L
e
L
x
e
k
q
L
x
TTTxT
µµ
µ
IVa.5.18
Since the slab temperature is maintained at both sides, there is a maximum tem-
perature within the slab obtained by setting the derivative of temperature in Equa-
tion IVa.5.18 equal to zero dT(x)/dx = 0:
()
()
»
¼
º
«
¬
ª
−+−
′′′
−=
− L
L
e
L
TT
Lq
k
x
µ
µ
µ
µ
1
1
ln
1
0
0
max
IVa.5.19
We then find the maximum temperature by substituting x
max
from Equa-
tion IVa.5.19 into Equation IVa.5.18. Since the flux decreases exponentially,
about 90% of the total energy is usually absorbed in the 15% of the thickness of
tering. In this case, the probability is shown as Σ and is known as the macroscopic cross
section. If the gamma rays are striking the surface of the medium, the type of interaction
may be pair production, Compton scattering, or photo electric. For more information see
El-Wakil and Lamarsh.

5. Analytical Solution of 1-D S-S Heat Conduction Equation, Slab 459
the medium, which is closer to the radiation source. Especially for thick mediums,
term e
–
µ
L
becomes exceedingly small and can be ignored.
Case 2. Specified Convection BC. In problems involving radiation heating, the
medium is generally cooled from both sides by convection heat transfer. At x = 0,
the convection boundary condition h
1
, T
f1
and at x = L, the convection boundary
condition h
2
, T
f2
is specified. In this case, coefficients c
1
and c
2
are found from:
At x = 0,
0)()/(
11
=−−−−
f
TThdxkdT
At x = L, 0)(/
22
=−−−
f
TThdxkdT
Solving for c
1
and c
2
, while ignoring e
–
µ
L
, we find the temperature profile in the
medium as:
101
12
0
2
2
12
10112
2
12
(1 / )( / )
(1 / 1 / )
(1 / )( / )
(/)
(1 / 1 / )
ff
x
f
ff
TT hkqh
q
TT e x
Lhhk
k
TT hkqh
Lkh
Lhhk
µ
µµ
µ
µµ
−
−++
′′′
′′′
−=− − +
++
−++
′′′
+
++
Similar to Case 1, the location of the maximum temperature is found from:
»
¼
º
«
¬
ª
++
′′′
++−
′′′
−=
khhL
hqkhTT
q
k
x
ff
)/1/1(
)/)(/1(
ln
1
21
10121
0
max
µµ
µ
µ
It is important to note that in both Cases 1 and 2, the total heat removed from the
medium being bombarded with radiation must exactly match the heat generated in
the medium by radiation (what if the heat removed is less than the heat gener-
ated?). Mathematically, the following balance at steady state operation must exist:
³
dxqTThTTh
L
0
02211
)()(
′′′
=−+−
Example IVa.5.6. In nuclear plants, the spent fuel assemblies are placed in a
spent fuel pool (SFP) filled with borated water. The pool wall consists of a steel
liner attached to thick concrete. It is important to maintain the humidity content of
the concrete. Thus, we want to determine the maximum temperature in the con-
crete due to the pool wall being irradiated by gamma rays emitted from the spent
fuel rods. In the solution we must account for heat generation in both steel and
concrete. Use the given data and the following subscripts; a: air, c: concrete, s:
steel liner, w: water. Ignore contact resistance.
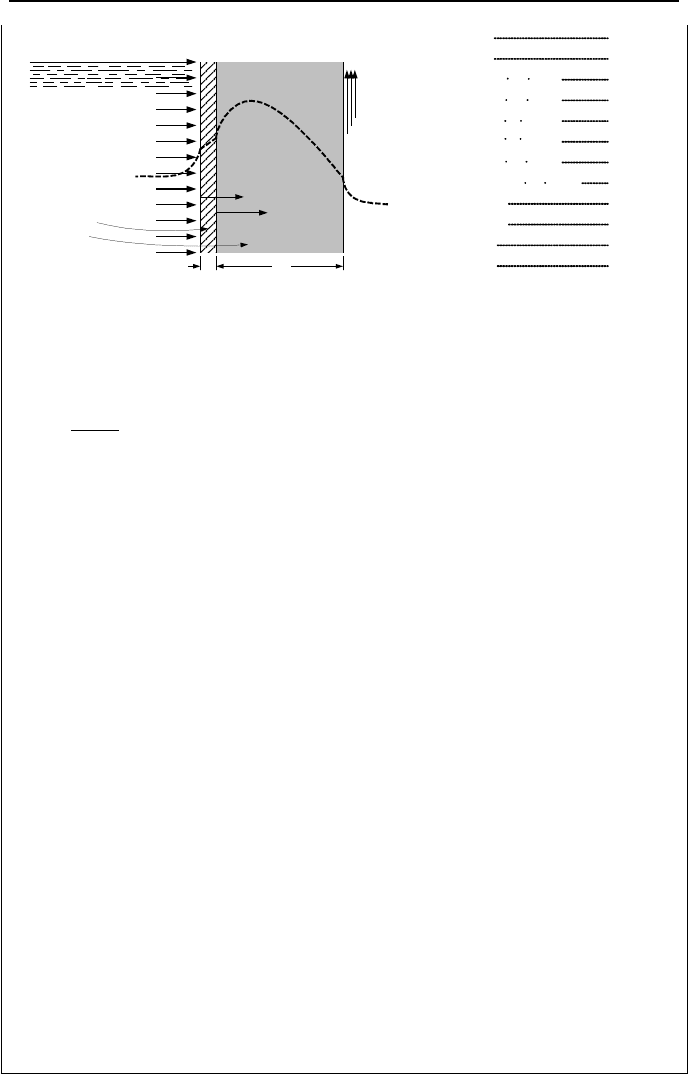
460 IVa. Heat Transfer: Conduction
Spent Fuel Pool
Steel Liner
Concrete
T
a
h
a
T
w
h
w
Air
Water
L
δ
x
s
x
c
T
w
(F):
T
a
(F):
h
w
(Btu/h ft
2
F):
h
a
(Btu/h ft
2
F):
k
s
(Btu/h ft F):
k
c
(Btu/h ft F):
130
100
50
1
s
q
′′′
(Btu/h ft
3
F):
c
q )(
0
′′′
(Btu/h ft
3
F):
10
0.8
1500
400
δ
(in):
L (ft):
µ
c
(ft
-1
):
5
5
0.5
µ
s
(ft
-1
):
14
Solution: Since the steel liner is thin, a constant
s
q
′′′
is specified. Steel tempera-
ture is given by:
21
2
)2/( cxcxkqT
sssss
++
′′′
−=
and concrete temperature by
43
2
0
cxce
k
q
T
c
x
cc
c
c
++
′′′
−=
−
µ
µ
. There are four unknown coefficients c
1
, c
2
, c
3
,
and c
4
and four boundary conditions at x
s
= 0, at x
s
=
δ
, and at x
c
= L:
At x
s
= 0, we have: –[–k
s
dT
s
/dx
s
] – h
w
(T
s
– T
w
) = 0
At x
s
=
δ
, we have: T
s
= T
c
At x
s
=
δ
, we have: –[–k
c
dT
c
/dx
c
] – [–k
s
dT
s
/dx
s
} = 0
At x
c
= L, we have: [–k
c
dT
c
/dx
c
] – h
a
(T
c
– T
a
) = 0
Representing )2/(
ss
kq
′′′
=
α
and )/(
2
,0
ccc
kq
µβ
′′′
=
, the four equations are found
as:
k
s
c
1
+ h
w
c
2
= h
w
T
w
–
αδ
2
+ c
1
δ
+ c
2
= –
β
+ c
4
k
c
(c
3
+
µβ
) + k
s
(–2
αδ
+ c
1
) = 0
(k
c
+ Lh
a
)c
3
+ h
a
c
4
= h
a
T
a
we find c
1
, c
2
, c
3
, and c
4
from:
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
−
−
=
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
+
−
aa
cs
ww
aac
cs
ws
Th
kk
Th
c
c
c
c
hLhk
kk
hk
µβαδ
βαδ
δ
2
00
00
101
00
2
4
3
2
1
For the given set of data, we find c
1
= –5.74, c
2
= 126, c
3
= –7.96, and c
4
= 146.
Hence, T
s
and T
c
become:
12674.533.83
2
+−−=
sss
xxT
and 14696.720
5
+−−=
−
c
x
c
xeT
c
, respectively.
The maximum temperature of T
c
= 140 F occurs in the concrete at x
c
= 6 in.
6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder 461
6. Analytical Solution of 1-D S-S Heat Conduction Equation, Cylinder
Determination of the heat transfer rate and temperature distribution in cylinders is
essential in many practical applications. This includes heat transfer from hollow
cylinders such as pipes and tubes as well as heat transfer from solid cylinders such
as nuclear fuel rods. In the discussion that follows, we have divided the topic of
heat transfer in cylinders into two sections based on whether internal heat genera-
tion exists in the cylinder or not. Each section is further divided into two subsec-
tions based on whether the cylinder is solid or hollow. The major distinction is the
type of boundary conditions applied to each case.
6.1. 1-D S-S Heat Conduction in Hollow Cylinders (
0=
′′′
q
)
Shown in Figure IVa.6.1 is a pipe with inside radius of r
1
and an outside radius of
r
2
, carrying a fluid at the bulk temperature of T
fa
. The pipe is exposed to the con-
vection boundary of T
fb
and h
b
. If temperatures of both inside and outside fluids
remain constant along the length of the pipe, the heat diffusion will be in the radial
direction. While similar solution applies whether T
fa
> T
fb
or T
fa
< T
fb
, in the deri-
vation below we have assumed T
fa
> T
fb
.
T
fb
r
1
r
2
T
2
T
1
T
fa
T
fb
, h
b
T
fa
, h
a
R
b
R
s
R
a
q q
L
T
fb
, h
b
T
fa
, h
a
Figure IVa.6.1. Hollow cylinder without internal heat generation
Our goal is to determine the steady state ( 0/ =∂∂ tT ) temperature distribution
in this hollow cylinder, assuming constant thermal conductivity (
0/ =∂∂ Tk ) and
no internal heat generation (
0=
′′′
q
). Since the thermal conductivity remains con-
stant, the applicable equation in this case is Equation IVa.2.7. Since we are only
concerned with heat diffusion in the
r-direction, we use the Laplacian in polar co-
ordinates as given by Equation IVa.2.8. For steady state, the Poisson equation re-
duces to:
0)(
1
2
==∇
d
r
dT
r
d
r
d
r
T IVa.6.1
Integrating this equation, we find dT/dr = c
1
/r. Hence, temperature in the cylinder,
as a function of radius, is given as
21
ln)( crcrT += . We find coefficient c
1
and
c
2
from the boundary conditions for three cases.
