Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

432 IVa. Heat Transfer: Conduction

goal is to find analytical solutions to both steady state and transient heat conduc-

tion problems. In this regard, we start with one-dimensional geometry in the Car-

tesian, cylindrical, and spherical coordinate systems. We consider such cases as

heat conduction with internal heat generation, which may in turn be a function of

space (i.e., location) or temperature. We then consider transient response of multi-

dimensional objects to heat conduction. This is followed by the introduction of

numerical methods.

1. Definition of Heat Conduction Terms

Homogenous versus heterogeneous: In conduction heat transfer

, a substance

is considered homogenous if its thermal conductivity, as defined later in this section,

does not vary from point to point within the substance. Otherwise, the substance is

heterogeneous. Water and iron, are examples of homogenous substances and such

porous materials as wood and cork are examples of heterogeneous material.

Isotropic versus anisotropic: A substance is considered isotropic with respect

to heat conduction when its thermal conductivity is the same in all directions.

Otherwise, the substance is anisotropic. Water and iron are examples of isotropic

and wood and asbestos are examples of anisotropic materials. In this chapter we

deal only with homogenous and isotropic materials.

Volumetric heat generation rate (

V/Qq



′′′

) is the rate of energy produced

in the unit volume of the substance by chemical, electrical, or nuclear reactions.

In British units, this term can be expressed as Btu/hr-ft

and in SI units it is gener-

ally expresses as W/m

. Nuclear reactions are discussed in Chapter V.

Heat flux (

AQq /



′′

) is the rate of heat transfer per unit area. In British units,

it is generally expressed as Btu/hr-ft

and in SI units as W/m

Linear heat generation rate (

LQq /



′

) is the rate of heat transfer per unit

length. In British units, it can be expressed as Btu/ft and in SI units as W/m. In

nuclear engineering, this term is often expressed in the hybrid unit of kW/ft.

Transport by diffusion is the mechanism responsible for thermal conduction.

For example, in gases at atmospheric pressure and temperature, a molecule travels

a short distance before colliding with another molecule. This collision results in

the transfer of energy in the gas in a tortuous path. The mean free path of a mole-

cule (l) is much smaller than the characteristic length of the system (L).

Fourier’s law of heat conduction, published in Theorie Analytique de la

Chaleur by Baron Jean Baptist Joseph Fourier (1768–1830) in 1822, provides the

most essential relation between the rate of heat transfer and the temperature gradi-

ent in heat conduction. In a substance, heat flows from a higher to a lower tem-

Although conductive and convective heat transfer are more proper, we retain the more tra-

ditional coduction and convection heat transfer.

1. Definition of Heat Conduction Terms 433

perature region. The higher the temperature difference ( T∆ = T

–T

) between

these regions (i.e. the temperature gradient) the higher the rate of heat transfer.

The rate of heat transfer is also proportional to the area normal to the direction of

heat (A), but the rate of heat transfer decreases as the distance between the two re-

gion (∆x) increases. We then conclude that:



∝

xTA ∆∆ /

IVa.1.1

Equation IVa.1.1, in which l << L, is Fourier’s law for homogenous isotropic con-

tinua.

Thermal conductivity as a transport property of a substance, is the proportion-

ality factor between the rate of heat flux and the temperature gradient with respect

to distance;

∂

−=



IVa.1.2

Since the temperature gradient is negative, the minus sign is inserted to get posi-

tive value for the rate of heat transfer in the direction of decreasing temperature.

Fourier’s law for heterogeneous isotropic continua can be generalized by using the

gradient operator:

Tkq ∇−=

′′



IVa.1.3

which is applicable in all three coordinate systems. In Cartesian coordinates,

Equation IVa.1.3 becomes:

)( k



∂

−=

′′

Thermal conductivity for some materials, such as wood for example, is direction-

ally dependent and must be treated as a tensor. The vectorial form of Fourier’s

law for heterogeneous anisotropic continua is:

Tq ∇⋅=

′′



where

is thermal conductivity tensor. This equation in Cartesian coordinate is

written as:

∂∂

−=

′′

kkk

zzzyzx

yzyyyx

xzxyxx



Thermal conductivity in British units is expressed as Btu/h·ft·F and in SI units as

W/m·C. The value of k for a continuum depends on several factors including

thermodynamic state (phase, pressure, and temperature) as well as chemical com-

position and structure. Values for some materials are shown in Figure IVa.1.1 and

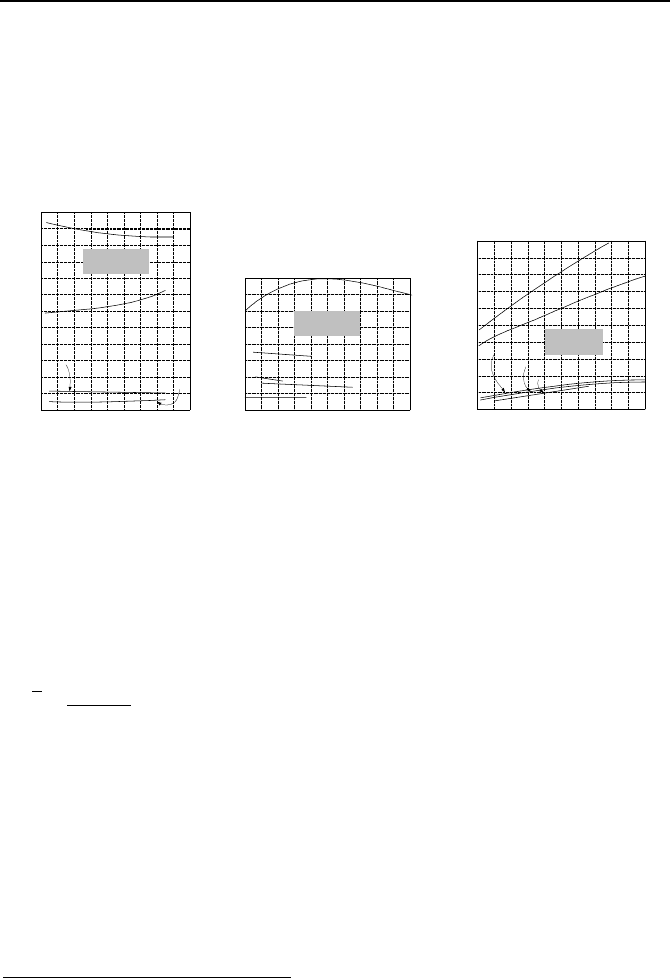
434 IVa. Heat Transfer: Conduction

in Appendix Tables A.IV.1 through A.IV.6. In metals where properties are pri-

marily a function of temperature, thermal conductivity can be correlated to tem-

perature as:

[]

)(1

000

TTkk −+=

IVa.1.4

where k

is thermal conductivity at a given reference temperature T

0 200 400 600 800

0.0

Temperature (F)

k (Btu/h ft F)

100

200

METAL

0 100 200 300 400 500

0.0

Temperature (F)

k (Btu/h ft F)

0.1

0.2

0.3

0.4

Saturated Water

Glycerin

Benzene

Light Oil

Freon 12

LIQUID

0 200 400 600 800 1000

0.0

Temperature (F)

k (Btu/h ft F)

0.2

0.1

Oxygen

Air

Carbon Dioxide

GAS

Figure IVa.1.1. Thermal conductivity of some metals, liquids, and gases

Due to its dependence on space and temperature, thermal conductivity can

complicate heat conduction analysis. Fortunately, in most cases thermal conduc-

tivity over the temperature range of interest can be treated as a constant, which

greatly simplifies analysis. Even in cases, such as calculation of heat transfer in

nuclear fuels, where thermal conductivity may not be treated as a constant, an av-

erage value for k may be determined over the temperature range of interest as:

kdT

−

IVa.1.5

Using a constant value, a linear function, or an average value over the temperature

range of interest for

k are all simplifying techniques in seeking analytical solutions

for heat conduction problems. In numerical solutions, there is no such limitation

for the specification of thermal conductivity.

Thermal capacitance, a thermodynamic property of a substance is defined as

the product of density and specific heat (

c). Thermal capacitance is an indication

of energy storage of a substance. As shown in Equation IVa.1.1, in conduction

heat transfer, density and specific heat always appear as an entity and only in tran-

Thermal conductivity of gases shown in this figure is for the viscous state. At the molecu-

lar state where gas pressure becomes exceedingly small (partial vacuum), k also becomes a

function of pressure. Roth gives the threshold pressure for the molecular state as P =

L(1 + C

T)] where L is the mean free path and constants C

and C

for air are 118.76

m/N and 0.00885 K

–1

, respectively. In this relation, P is in bar and T in degrees Kelvin.

1. Definition of Heat Conduction Terms 435

sient conduction. Thermal capacitance has units of Btu/ft

·F in British units and

J/m

·C in SI units.

Thermal diffusivity is defined as the ratio of thermal conductivity to thermal

capacitance

= k/

c. Although, this property is obtained by dividing a transport

property by a thermodynamic property, thermal diffusivity itself is the key trans-

port property for transient conduction. A small value for

indicates that the

substance has a higher potential to store energy than to transfer energy. A large

value for

indicates that the substance is more effective in transferring than in

storing energy. In British units, thermal diffusivity is expressed as ft

/s and in SI

units as m

/s.

Convection heat transfer (

′′



), is a mechanism by which heat is transferred

due to the bulk motion of a fluid. Of specific interest is the heat transfer between

a fluid in motion at one temperature and a solid at a different temperature. If the

fluid bulk motion is solely due to the existing temperature gradient between the

fluid and the solid, the convection is known as natural or free convection as op-

posed to forced convection. Mixed convection is a mode of heat transfer in which

the rate of heat transfer from free convection is comparable to that of forced con-

vection. Convection heat transfer is discussed in Chapter IVb.

Heat transfer coefficient. Similar to conduction, the rate of heat flux in con-

vection heat transfer is proportional to the temperature gradient,

Tq ∆∝

′′



. The

proportionality constant is known as the heat transfer coefficient,

Tqh ∆

′′

= /



. In

British units,

h is expressed as Btu/h·ft

·F and in SI units as W/m

·K. The rela-

tionship expressed as

Thq ∆=

′′



is known as Newton’s law of cooling. Orders of

magnitude of

h for various heat transfer regimes are shown in Table IVa.1.1.

Table IVa.1.1. Approximate range of convection heat transfer coefficient

Regime h (Btu/ft

·h·F) h (W/m

·K)

Free convection (air): 1 – 5 5 – 25

Free convection (Water) 10 – 250 50 – 1200

Forced convection (air): 5 – 50 25 – 250

Forced convection (water) 10 – 5000 50 – 20,000

Condensation of steam on walls 500 – 5,000 2,000 – 20,000

Condensation of steam on pipes 500 – 10,000 2,000 – 50,000

Pool boiling of water 500 – 10,000 2,000 – 50,000

Flow boiling of water 500 – 20,000 2,000 – 100,000

Thermal resistance, (R

) depends on thermal conductivity of a substance,

however, it is not a property of the substance, as its value depends on the geome-

try in a specific problem. According to Fourier’s law, )/(

xTkAQ ∆∆=



. Using an

electrical engineering analogy, the temperature gradient resembles applied voltage

and the rate of heat transfer resembles electric current. Thus, R

= ∆x/(kA) can be

viewed as thermal resistance. Obviously, substances with higher thermal conduc-

436 IVa. Heat Transfer: Conduction

tivity and larger surface area pose smaller resistance to the flow of heat. Con-

versely, the larger the distance between two regions of higher and lower tempera-

tures, the lower the rate of heat transfer. Thermal resistance in convection heat

transfer can also be obtained as R

= 1/(hA) where h is the heat transfer coeffi-

cient.

Contact resistance occurs in thermal conduction between two attached solids.

In such cases, there is always a gap between the two solids due to surface rough-

ness. The only exception is when surfaces in contact are mirror finished. In most

applications, the gap between the two surfaces of solids in contact is filled with

stagnant air, which is a poor conductor of heat. As a result, there is a thermal re-

sistance in addition to the heat conduction resistance for surfaces in contact. Ex-

pectedly, the contact resistance depends on both the pressure applied to the com-

posite solids and the fluid filling the gap. As a rough estimate, the contact

resistance may be taken into account by increasing the thickness of the solid with

lower thermal conductivity by about 0.2 in (5 mm).

Radiation heat transfer (

′′

) refers to the exchange of thermal radiation be-

tween surfaces. Thermal radiation is the energy emitted due to the internal energy

of the surface, manifested as temperature. Unlike the conduction and convection

modes, radiation does not require a medium as the emitted energy is transported

by photons capable of traveling through perfect vacuum. The mean free path in

radiation heat transfer is very long compared with the diffusion mechanism since

photons travel in straight lines without colliding. The Stefan-Boltzmann law gives

the maximum rate of heat transfer radiated from a surface as

′′

where T

is the absolute temperature of the surface and the Stefan-Boltzmann constant is

given as

= 0.1714E-8 Btu/h·ft

·R

= 5.67E-8 W/m

·K

. A surface exhibiting the

maximum rate of heat transfer is known as a black body. Real surfaces are those

that emit less energy by a factor of

, known as emissivity. The net radiation heat

flux between two surfaces, located in a radiationally non-participating medium, is

found from

().

qTT

εσ

=−

′′



In this equation,

is the surface emissivity and

is the temperature of surface 2, which encompasses surface 1. It is shown in

Chapter IVd that the net heat flux should be reduced by a view factor if only some

of the radiation leaving surface 1 reaches surface 2. While radiation heat transfer

is always present, at low temperatures it may become insignificant when com-

pared with the rate of heat transfer by forced convection mechanism. An example

of neutron and gamma radiations, which must be treated differently than thermal

radiation, is given in Section 5.5 of this chapter.

Steady state (S-S) conduction refers to a condition where temperature distribu-

tion in a substance does not change with time. As such, any heat added to the sub-

stance or internally produced in the substance is transferred away from the sub-

stance. Selection of insulation to minimize heat loss from a piping system

carrying superheated steam is based on a steady state analysis. Similarly, design

of fins or extended surfaces to maximize the rate of heat dissipation from elec-

tronic devices or air-cooled engines involves steady state application of the con-

duction heat transfer. Steady state operation of a nuclear core implies that the rate

2. The Heat Conduction Equation 437

of heat production by fission in the fuel rods is exactly equal to the rate of heat

removal by the coolant. Mathematically speaking, the solution to steady state

problems is obtained if the algebraic summation of all energy addition, generation,

and removal from a control volume is set equal to zero. This reflects the fact that

while temperature changes from point to point inside the object, the distribution of

temperature remains the same and is independent of time.

Unsteady, time-dependent, or transient conduction heat transfer deals with the

temperature response of an object to changes in the rate of internal heat generation

(if any) or changes in the boundary conditions. Problems dealing with cooling

down or heating up of a substance are transient in nature. Mathematically speak-

ing, changes in the rate of internal heat generation (if any) or changes in the

boundary conditions are forcing functions for temperature distribution.

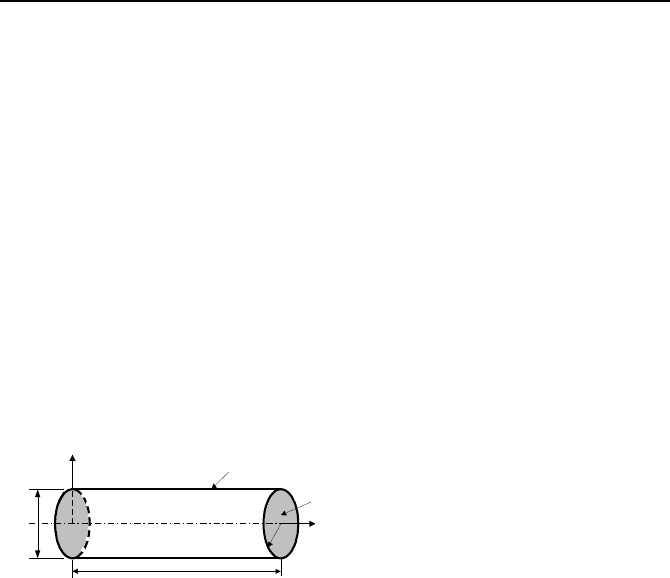
Heat transfer area. Distinction must be made between the surface and the

cross sectional areas. For the solid cylinder shown in Figure IVa.1.2, area at x = 0

= =

/4 while area at y = r

is S =

DL.

A: Cross sectional area

S: Surface area

Figure IVa.1.2. Identification of cross sectional area and surface area

Fourier number (Fo =

/ xt

) is a dimensionless number pertinent to tran-

sient analysis in conduction.

2. The Heat Conduction Equation

We may directly derive the heat conduction equation by using the differential

analysis for heat diffusion in an infinitesimal control volume. The analysis is per-

formed in the Cartesian coordinate system as shown in Figure IVa.2.1. The deri-

vation is based on the first law of thermodynamic We simplify Equation IIa.6.3 by

noting that for the infinitesimal control volume

¦¦¦

=== 0Wmm





so that:

energyinternalof

changeofRate

radiation&conduction

byremovalheatofRate

generationheat

internalofRate

radiation&conduction

byaddition heatofRate

The total rate of energy entering the C.V. from all sides by conduction is:

438 IVa. Heat Transfer: Conduction

dxdzdy

][

∂



dxdydz

][

∂



dydzdx

][

∂



dxdyq



dxdzq



dydzq



∆z

∆y

∆x

dxdydzq

′′′



Figure IVa.2.1. Diffusion of heat in an elemental control volume in Cartesian coordinates

dxdydzqqq

zyx

)(

"""



The total rate of energy leaving the C.V. from all sides by conduction is:

dydzdxxqqdydzdxxqqdydzdxxqq

xxxxxx

])/([])/([])/([

""""""

∂∂++∂∂++∂∂+



If there is any internal heat generation (due to nuclear reaction, electrical resis-

tance, or exothermic chemical reaction, for example), then the total rate of energy

produced in the C.V. is:

dxdydzq

′′′



Using our sign conventions of Chapters II and III, we find the rate of change of to-

tal energy of the C.V. as:

tuqzqyqxq

zyx

∂∂=

′′′

+∂∂+∂∂+∂∂ /)()]/()/(/[

"""



Taking advantage of Fourier’s law, the result in the absence of noticeable thermal

radiation can be cast in the general form of:

[]

trT

TrcTrtrqtrTTrk

∂

′′′

+∇⋅∇

),(

),(),(),(),(),(



IVa.2.1

The definition of each term in Equation IVa.2.1 is as follows:

[]

),(),( trTTrk

∇⋅∇ : rate of heat transfer by conduction mechanism

),( trq



′′′

: rate of internal heat generation per unit volume

trT

TrcTr

∂

∂ ),(

),(),(

: rate of change of internal energy of the control volume

It is emphasized in Equation IVa.2.1 that in general the material thermal properties

are functions of space and temperature. This is especially true for thermal conduc-

tivity as discussed earlier. In special cases where thermal properties can be con-

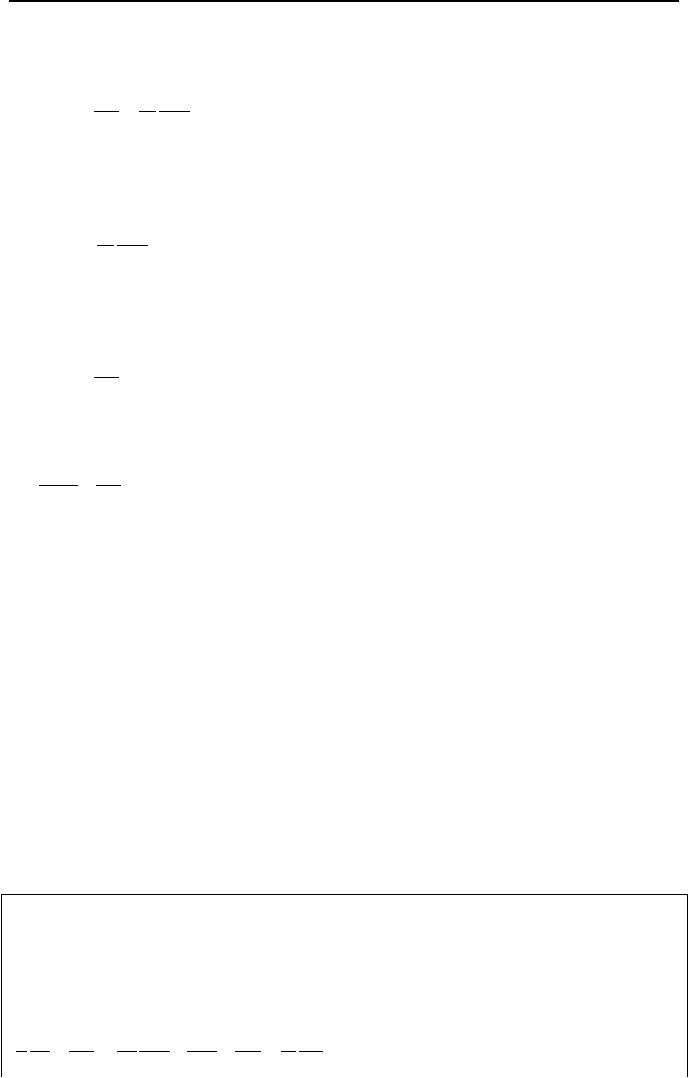
2. The Heat Conduction Equation 439

sidered constant over the temperature range of interest, the above equation can be

simplified to obtain the general heat conduction equation:

∂

′′′

+∇



IVa.2.2

In the absence of any internal heat generation, the equation takes the form of the

Fourier equation:

∂

=∇

IVa.2.3

In steady state with internal heat generation, the equation becomes the Poisson

equation:

′′′

+∇



IVa.2.4

In one-dimension, Equation IVa.2.4 in the Cartesian coordinate simplifies to:

′′′



IVa.2.4-1

If the internal heat generation is not uniform, rather is a linear function of

temperature, the Poisson equation becomes the Helmholtz equation:

=+∇ TCT IVa.2.5

where

C is a constant. The Laplacian term (

∇ ) can be expanded depending on

the application of the Poisson equation in the Cartesian, cylindrical, or spherical

coordinate systems. Under steady state conditions and with

′′′



, the Poisson

equation reduces to:

=∇ T IVa.2.6

And in the one-dimensional Cartesian coordinate, Equation IVa.2.6 can be simply

written as d

T/dx

= 0. The following example deals with conduction equation in

the cylindrical coordinates.

Example IVa.2.1. Write the general heat conduction equation in the cylindrical

coordinate system. (k = constant)

Solution: Substituting for the Laplacian operator from Equation VIIc.1.10, we

find;

22 2

11 1

()

TTTqT

rr r k trz

αθ

′′′

∂∂ ∂ ∂ ∂

+++=

∂∂ ∂∂∂



IVa.2.7

440 IVa. Heat Transfer: Conduction

For long cylinders having symmetry in the

-direction, temperature becomes only

a function of r. Hence, Equation IVa.2.7 reduces to the one-dimensional heat

conduction equation in polar coordinate:

()

Tq T

rr r k t

′′′

∂∂ ∂



IVa.2.8

Example IVa.2.2. Write the general heat conduction equation in the spherical

coordinate system. (k = constant)

Solution: Substituting for the Laplacian operator from Equation VIIc.1.11, we

find;

∂

′′′

∂

αφ

φθφ

)(sin

sin

)(



IVa.2.9

For symmetrical conditions along

and

, temperature becomes only a function of

distance r. Hence, Equation IVa.2.9 reduces to one-dimensional heat conduction

in the spherical coordinate system:

∂

′′′

∂

)(



IVa.2.10

2.1. Initial and Boundary Conditions

Once the differential equation for heat conduction is obtained, we need to have the

boundary and the initial conditions to obtain the solution for a specific problem.

Boundary conditions (BC) are required whether we seek analytical or numeri-

cal solutions to steady state or transient problems. As Equation IVa.2.1 shows, the

heat conduction equation is a second order differential equation in space and a

first order differential equation in time. Hence, it requires two boundary condi-

tions and one initial condition. Basically, there are four types of boundary condi-

tions

that may be prescribed; temperature at the boundary, constant heat flux,

thermal radiation, and a convection boundary. An insulated boundary is a special

case of the constant heat flux boundary condition where

′′



. Let’s now dis-

cuss each of these four types.

Temperature BC: The prescribed surface temperature is referred to as the

Dirichlet boundary condition. If the specified boundary temperature is T

, then

)

= T

where subscribe b stands for boundary. The specified temperature at

the boundary may not necessarily be a constant. Rather the prescribed tempera-

ture in general may vary as a function of time.

Other more complicated boundary conditions include such cases as phase change and

thermal resistance.

2. The Heat Conduction Equation 441

Heat flux BC is also known as the Neumann boundary condition. The pre-

scribed heat flux may be into or away from the boundary. We assign a positive

sign to the heat flux if it is towards the boundary and a negative sign if it leaves

the boundary. Hence, for a heat flux BC we write

′′



, where

′′



is the

heat transfer by conduction in the solid at the boundary and

′′

is the prescribed

heat flux at the boundary. Alternatively, we can write

[]

0)/( =

′′

±∂∂−±

qnTk



where n is the direction normal to the boundary. Note that if the heat flux at the

boundary is prescribed as zero (

′′



), it is implies that the boundary is insu-

lated. A zero heat flux is also an indication of temperature symmetry in a sub-

stance.

′′



′′



′′

−

′′



′′



′′



′′

−



Radiation BC may be due to thermal radiation of the solid at the boundary or a

prescribed radiation heat flux at the boundary. The effect of incoming thermal ra-

diation is to raise the boundary temperature. This is different than a bombardment

of solids with high-energy radiation, such as gamma heating, which results in in-

ternal heat generation in the solid, as discussed in Section 5.5.

Convection BC: Specification of a heat transfer coefficient at the boundary

implies the exchange of heat by the conduction and convection mechanisms so

that ±[–k(

∂

] ± h(T

– T

) = 0 where T

is the fluid temperature at the bound-

ary. A convection boundary condition is usually shown by h, T

. Figure IVa.2.2

shows three examples for convection boundary conditions.

)(

fbc

TThq −=

′′



′′

′′

−

′′





crn

qqq

′′

−

′′

′′ 

′′

−

crn

qqq



′′

′′



′′



(a) (b) (c)

Figure IVa.2.2. Examples of convection and radiation boundary conditions

In case (a), heat brought to the boundary by conduction is carried away from

the boundary by convection. In case (b), heat brought to the boundary by conduc-