Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

IIIc. Fluid Mechanics: Compressible Flow

402

A. Pressure Drop for Flow of Compressible Fluids in Pipelines,

Reduction from General Formula

Consider the flow of an ideal gas in a pipe with diameter D. If flow properties are

known at the inlet (i), we want to find flow properties at the outlet (e) for T

i

= T

e

.

We try this method only for pressure. Here, dA = 0 (pipe with constant flow area)

and dT = 0 (isothermal process). Equation IIIc.1.12 reduces to:

¸

¹

·

¨

©

§

−

+−

−

¸

¹

·

¨

©

§

−

=

RT

dF

Tc

dq

P

dP

p

2

Ma1

1Ma)1(

Ma1

Ma

γγ

and Equation IIIc.1.13 yields:

0

Ma1

Ma)1(

Ma1

2

=

¸

¹

·

¨

©

§

−

¸

¹

·

¨

©

§

−

RT

dF

Tc

dq

p

γγ

We find (dq/c

p

T) from the second equation and substitute in the first. After sim-

plification we find:

¸

¹

·

¨

©

§

−

=

RT

dF

P

dP

1Ma

1

2

γ

If we substitute for Ma

2

= V

2

/

γ

RT, for dF = (4/

ρ

)(dx/D)

τ

w

, and for

τ

w

=

(f/4)(

ρ

V

2

/2), we get

1

2

1

2

−

¸

¹

·

¨

©

§

−=

V

P

D

Pf

dx

dP

ρ

IIIc.1.16

Equation IIIc.1.16 can be integrated to obtain ∆P. We will further study Equation

IIIc.1.16 in Section 2.

B. Pressure Drop for Flow of Compressible Fluids in Pipelines,

Direct Derivation

Here we derive the equation for pressure drop between two points i and e directly

from the conservation equations. These points are located at a distance L from

each other on a horizontal pipe having diameter D. For this section of pipe, as-

suming steady flow, Equation IIIa.3.28 simplifies to:

0h

1

=++

f

d

g

VdVdP

g

ρ

where dh

s

is also dropped since there is no shaft work between the points. Substi-

tuting for the frictional head loss from Equation IIIb.3.4 for a differential length dx

given as:

1. Steady Internal Compressible Viscous Flow

403

g

V

D

dx

fd

f

2

h

2

=

we obtain:

0

2

=++

V

D

dx

fVdV

dP

ρ

IIIc.1.17

To be able to differentiate Equation IIIc.1.17, we eliminate both density and ve-

locity. To accomplish this, we first divide through by V

2

, knowing that V ≠ 0:

0

2

=++

D

dx

f

V

dV

V

dP

ρ

IIIc.1.18

To eliminate

ρ

and V, we need two additional equations. First we use the continu-

ity equation. The density and velocity at any point along the flow path can be re-

lated to the given density and velocity at the production source for steady flow:

GAmAVVA

ii

===



ρρ

The second equation is the ideal gas equation of state, RTP =

ρ

/ from which,

PRT //1 =

ρ

. The first term in Equation IIIc.1.18 can be manipulated, noting

that for T

i

= T we have P

i

/

ρ

i

= P/

ρ

, to get:

iiii

i

iiii

i

ii

VP

P

VP

dPRT

VVP

dPRT

VV

dP

V

dP

)()

1

)((

1

2

===

ρ

Similarly, we manipulate the second term of Equation IIIc.1.18, using V = G/

ρ

=

GRT/P, to get:

P

dP

P

GRTdP

GRT

P

dV

V

−=−= ))(()

1

(

2

Equation IIIc.1.18 then simplifies to:

0

2

)(

2

=++−

D

dx

f

VP

PdP

RT

P

dP

ii

i

This equation can now be integrated for flow from one point to another:

2

0

() 2

ee

e

i

ii

Px

P

i

P

Px

ii

dP RT dx

PdP f

PPV D

´´

µµ

¶¶

−+ + =

³

where x

i

and x

e

are points where pressure is P

i

and P

e

, respectively and x

e

– x

i

= L.

Integrating yields:

IIIc. Fluid Mechanics: Compressible Flow

404

01ln

2

=+

»

¼

º

«

¬

ª

¸

¹

·

¨

©

§

−−

¸

¹

·

¨

©

§

−

D

L

f

P

V

RT

P

i

e

i

e

IIIc.1.19

where the subscript for temperature is dropped, as T

e

= T

i

. Equation IIIc.1.19 may

alternatively be written as:

()

0ln

211

=−−− ccc

ξξ

IIIc.1.19

where the dummy variable

ξ

and coefficients c

1

and c

2

are given as:

ξ

= (P

e

/P

i

)

2

1

/

i

VRTc =

c

2

= fL/D

In this integration, we assumed the friction factor remains constant between the

two points. This is a valid assumption as the friction factor for smooth pipes is a

function of the Reynolds number (Equation IIIb.3.3), which is in turn a function of

viscosity (Re =

ρ

VD/

µ

). For ideal gases, viscosity is only a function of tempera-

ture, which was assumed to remain constant (isothermal flow).

Equation IIIc.1.19 is a non-linear algebraic equation, which should be solved

by iteration. As the first guess, we may ignore ln ȟ, compared with the absolute

value of the other two terms, and find ȟ from:

2

Ma11

i

e

D

L

f

RT

V

D

L

f

P

γξ

−=−=

¸

¹

·

¨

©

§

= IIIc.1.20

Example IIIc.1.1. Air flows isothermally in a smooth, 1 ft (0.3 m) diameter, 1500

ft (457 m) long horizontal pipe at a rate of 7500 CFM (212.4 m

3

/min). Air enters

the pipe at 600 psia (4.1 MPa) and 300 F (149 C). Find the pressure drop in the

pipe.

Solution: At given P

i

and T

i

, air viscosity is v

i

= 1.27E-5 ft

2

/ s. We now perform

the following steps:

22

ft785.04/14.34/14.3 === DA (0.073 m

2

)

ft/s15.159)60785.0/(7500/V

1

=×== AV



(48.5 m/s)

Re / 159.15 1/1.27E 5 1.25E7;

ii i

VD v==× −=

007.0)6E88.5/(184.0Re/184.0

2.02.0

===

ii

f

. Since f

i

= f

e

, we drop the subscript.

53.51)2.32/15.159/()460300)(97.28/1545(/

22

1

=+==

i

VRTc

,

5.101/1500007.0/

2

=×== DfLc

. Therefore, Equation IIIc.1.19 becomes:

51.53ȟ – ln(ȟ) – 41.03 = 0

1. Steady Internal Compressible Viscous Flow

405

By iteration, we find;

ξ

§ 0.792. Thus, (P

e

/P

i

) = (0.792)

1/2

= 0.8899

P

e

= 0.8899 × (600) = 534 psia and pressure drop is ∆P = P

i

– P

e

= 600 – 534 = 66

psi (0.455 MPa)

If estimated from Equation IIIc.1.20, ȟ is found as:

ȟ = 1 – [0.007 × (1500/1.0) × (159.15

2

/32.2)]/[(1545/28.97) × (300 + 460)] =

0.796.

Caveat: Pressure drop associated with the isothermal flow of compressible

viscous fluids results in a decrease in the fluid density, which in turn results in an

increase in the flow velocity to preserve the specified steady state mass flow rate.

Equation IIIc.1.19 is valid only if flow remains subsonic. As is discussed in Sec-

tion 2, flow becomes sonic when dP/dL

ĺ. We then take the derivative of

Equation IIIc.1.19:

()()

()

iiei

e

PPPVRT

Df

dL

dP

/2//2

/

22

−

=

IIIc.1.21

Setting the denominator of Equation IIIc.1.21 equal to zero, we find the condition

for sonic velocity as:

RT

V

P

i

e

2

=

¸

¹

·

¨

©

§

=

ξ

IIIc.1.22

Alternatively, we may express Equation IIIc.1.22 in terms of the Ma number by

noting that:

()

e

i

e

i

e

i

e

i

e

V

AVm

RT

P

Ma

/

====



ρ

IIIc.1.23

where we also took advantage of c

2

=

γ

RT and Ma = V/c. Substituting for the

pressure ratio in terms of the Mach number ratio in Equation IIIc.1.22, we find the

limiting Mach number:

γ

/1Ma

*

= IIIc.1.24

Thus Equation IIIc.1.19 is valid as long as the Ma number at the pipe exit remains

less than (1/

γ

)

1/2

.

Equation IIIc.1.19 may also be expressed in terms of the Ma number by using

the relation between the pressure ratio and the Mach number ratio, as given by

Equation IIIc.1.23:

»

¼

º

«

¬

ª

−

¸

¹

·

¨

©

§

+=

¸

¹

·

¨

©

§

D

L

f

e

i

e

i

2

Ma

lnMa1

Ma

γ

IIIc.1.25

IIIc. Fluid Mechanics: Compressible Flow

406

Example IIIc.1.2. Methane enters a pipeline at a rate of 50 kg/s. The pipe is

1200 m long, having an inside diameter of 0.5 m. Find the pipe length over which

Equation IIIc.1.19 is applicable.

Data: P

i

= 0.5 MPa, T

i

= 27 C, f = 0.015, M

CH4

= 16, and

γ

CH4

= 1.3.

Solution: We first calculate the Mach number at the pipe inlet:

A =

π

D

2

/4 =

π

(0.5)

2

/4 = 0.196 m

2

ρ

i

= P

i

/RT = 500/[(8.314/16) × (27 + 273)] = 3.207 kg/m

3

V

i

= )/( Am

i

×

ρ



= 50/[3.207 × 0.196] ≈ 79.55 m/s

=+××== )27327()16/8314(3.1RTc

γ

450 m/s

Ma

i

= 79.55/450 = 0.177

The limiting Mach number is then found as Ma

*

= (1/1.3)

0.5

= 0.877. Thus,

ξ

=

(Ma

i

/Ma

*

)

2

= 0.078

From Equation IIIc.1.25 we find:

»

¼

º

«

¬

ª

¸

¹

·

¨

©

§

−

−=

2

Ma

1

ln

i

f

D

L

γ

ξ

= =

»

¼

º

«

¬

ª

¸

¹

·

¨

©

§

×

−

2

177.03.1

1078.0

)078.0ln(

015.0

5.1

2008 m

Example IIIc.1.3. Express the relation for pressure drop for incompressible flow

in terms of the Ma number.

Solution: We substitute for

ρ

= P/(RT) and V

2

= c

2

Ma

2

= (

γ

RT)Ma

2

in Equa-

tion IIIb.3.7, P

i

– P

e

= (fL/D)

ρ

V

2

/2:

2

Ma

2

1

γ

D

L

f

P

i

e

−= IIIc.1.26

2

Ma

2

γ

D

L

fP =∆

1.3. Adiabatic Process for Compressible Fluids

Consider the same condition as discussed before. However, this time T

e

≠ T

i

but

the pipe is insulated so that dq = 0. Note that if there is also not any friction, the

problem can be easily solved using isentropic relations. However, we are consid-

ering adiabatic flow of gases with friction. To derive the formulation, we note that

for adiabatic (dq = 0) and constant area channel (dA = 0), Equations IIIc.1.13 and

IIIc.1.14 reduce to:

¸

¹

·

¨

©

§

−

−=

RT

dF

T

dT

2

Ma1

Ma)1(

γ

IIIc.1.27

1. Steady Internal Compressible Viscous Flow

407

¸

¹

·

¨

©

§

−

=

RT

dF

V

dV

2

Ma1

1

IIIc.1.28

Dividing Equation IIIc.1.27 by Equation IIIc.1.28 and substituting from Equa-

tion IIIc.1.28 yields:

¸

¹

·

¨

©

§

−−=

V

dV

T

dT

2

Ma)1(

γ

=

¸

¹

·

¨

©

§

−

−−

=

¸

¹

·

¨

©

§

−−

RT

dF

V

dV

2

Ma1

Ma)1(

γ

IIIc.1.29

Next, we substitute for dT/T from Equation IIIc.1.29 and for dV/V from Equa-

tion IIIc.1.28 into Equation IIIc.1.11. To deal with the dF/RT term, we find dF

from Equation IIIc.1.3 and V

2

from the definition of the Ma number dF/RT =

f(dx/2D)V

2

/RT = f(dx/2D)Ma

2

γ

RT/RT = f(dx/2D)Ma

2

γ

to obtain:

()

D

dx

f

d

»

¼

º

«

¬

ª

−

+

−

=

2

Ma

2

1

Ma1

Ma

γγ

IIIc.1.30

To make interesting conclusions from Equation IIIc.1.30, we also simplify

Equation IIIc.1.12 and like before substitute for dF = (4/

ρ

)(dx/D)

τ

w

,

τ

w

=

(f/4)(

ρ

V

2

/2), and

ρ

= P/RT to obtain:

2

1

Ma1

Ma)1(1

2

V

D

f

dx

dP

ργ

−

−+

−=

IIIc.1.31

Subsonic flow, Ma < 1 (dMa > 0). The pressure drop resulted from subsonic

flow of compressible viscous fluids in constant area conduits results in an increase

in the flow temperature, which combined with decrease in pressure (dP/dx < 0)

causes density to decrease (

ρ

= P/RT) and velocity (V = m



/

ρ

A) and Ma number to

increase. Thus, friction causes the subsonic flow to accelerate.

Supersonic flow, Ma > 1 (dMa < 0). The supersonic flow of compressible

viscous fluids in constant area conduits results in a decrease in Ma number and ve-

locity, requiring flow density and consequently pressure (dP/dx > 0) to increase.

Thus, supersonic flow decelerates due to friction. We further deal with this topic

in Section 2. But for now, let’s integrate Equation IIIc.1.30 from the pipe entrance

to the pipe exit:

()

[]

()

L

D

f

D

dx

fd

L

i

e

i

=

µ

¶

´

=

»

¼

º

«

¬

ª

−

+

−

=

µ

¶

´

−

−+

0

2

Ma

2

24

2

Ma

2

1

12

Ma1

ln

2

1

Ma

Ma1

Ma

)Ma1(Ma2

Ma12

γ

γγ

γ

IIIc.1.32

where in Equation IIIc.1.32, we have used an average value for the friction factor

and specified Ma

e

= 1. This results in the maximum pipe length beyond which

flow becomes sonic and supersonic. Since a supersonic flow decelerates, the tran-

IIIc. Fluid Mechanics: Compressible Flow

408

sition to subsonic is followed by a shock wave. The phenomenon is similar to a

hydraulic jump for the flow of incompressible fluids in open channels where a fast

and shallow flow becomes a slow and deep flow. As a result, Equation IIIc.1.32

gives the maximum pipe length for a continuous flow.

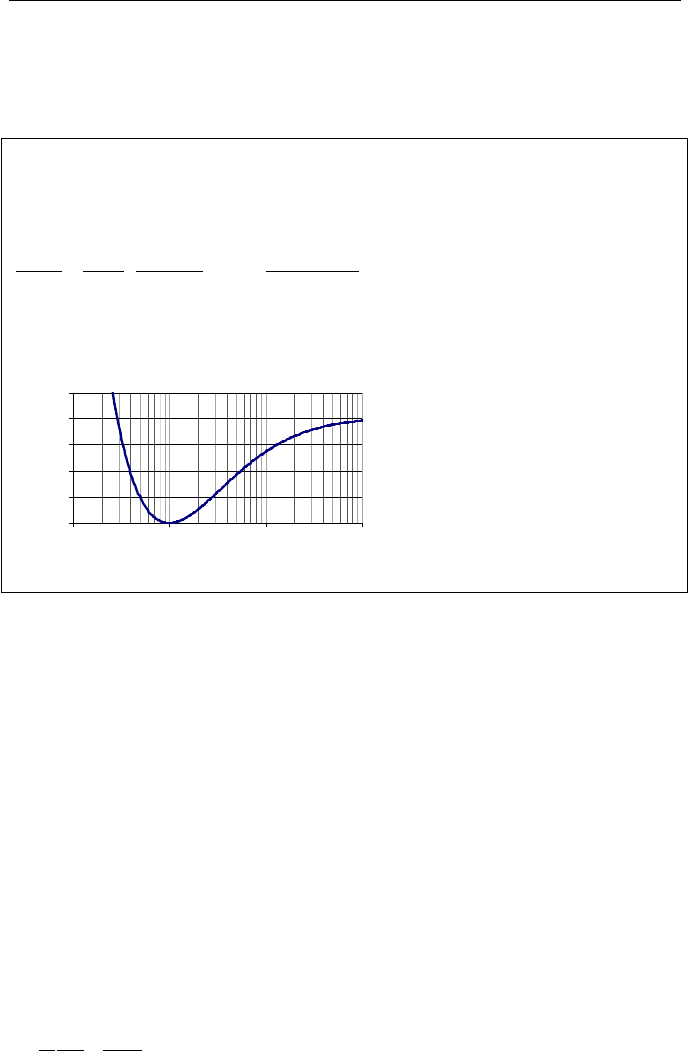
Example IIIc.1.4. Find the L

max

/D versus Ma

2

for air. Use an average friction

factor of 0.02.

Solution: We use Equation IIIc.1.32, which for air (

γ

= 1.4) becomes:

¸

¹

·

¨

©

§

+

−

=

2

max

Ma2.01

.2Ma1

ln2.1

Ma

Ma1

4.1

1

i

fD

L

The plot shows that as Ma

2

approaches , L

max

/D asymptotically approaches

about 40.

0

10

20

30

40

50

0.1 1 10 100

Ma

2

L

max

/D

1.4. Isentropic Process of Compressible Fluids

Under the isentropic process, we discuss two topics. First, we discuss the calcula-

tion of pumping power in compressors. Second, we consider compressible flow

through Bernoulli obstruction meters. The latter topic is especially important in

the measurement of compressible flow.

A. Calculation of Compressor Pumping Power

Pumping compressible fluids is an example of noticeable change in fluid density

during a process. Let’s consider a pipeline in which an ideal gas enters at pres-

sure P

1

(Figure IIIc.1.2). Due to the frictional losses, pressure drops downstream

to P

2

. Our goal is to find the pumping power required for increasing the pressure

of a compressible fluid from pressure P

2

to pressure P

3

. In a special case, P

3

= P

1

.

For the compressor as the control volume, we use Equation IIIa.3.28 while ignor-

ing frictional pressure drop and the change in elevation from the inlet to the outlet

of the compressor:

0h

1

=++

s

d

g

VdVdP

g

ρ

1. Steady Internal Compressible Viscous Flow

409

P

3

P

1

P

2

h

s

Compressor

Figure IIIc.1.2. Isentropic compression of an ideal gas

Using subscript 2 for the inlet to the compressor and subscript 3 at the exit of the

compressor, the rate of work delivered to the compressor shaft, in terms of shaft

head is found by integrating the above equation:

»

¼

º

«

¬

ª

µ

¶

´

+

−

−=

3

2

3

1

2

h

ρ

dP

gg

VV

s

IIIc.1.33

If heat transfer in the compressor is neglected, the compression process between

points 2 and 3 becomes adiabatic. Since we also assumed no frictional losses in

the compressor, we can write:

γγ

ρ

P

=

2

Therefore,

γ

ρρ

/1

22

)/)(/1(/1 PP= and upon substitution, the second term on the

right side of Equation IIIc.1.33 becomes:

»

¼

º

«

¬

ª

−

¸

¹

·

¨

©

§

−

=

»

¼

º

«

¬

ª

−

¸

¹

·

¨

©

§

−

=

−−

³

1

2

3

2

1

2

3

2

3

2

/1

1

2

γ

ργ

γ

ρ

P

RT

gP

P

g

dPPP

g

The first term in the right side of Equation IIIc.1.33 can also be rearranged to ob-

tain:

)1(

2

)1(

2

)1(

22

2

3

2

1

2

3

2

3

2

3

2

3

2

3

P

g

V

g

V

g

V

g

VV

−=−=−=

−

ρ

Note that conditions at point 3 must be identical to conditions at point 1. Substi-

tuting for the first and the second terms in the right side of Equation IIIc.1.33, the

required shaft head is calculated as:

»

¼

º

«

¬

ª

−

+−−=

−

)1(

1

)1(

2

h

1

2

1

γ

rRT

g

r

g

V

s

IIIc.1.34

IIIc. Fluid Mechanics: Compressible Flow

410

where the compression ratio r = P

3

/P

2

. Finally, the pumping power is determined

from:

ss

gmW h



= IIIc.1.35

where

m



is the mass flow rate of the compressible fluid through the compressor.

Example IIIc.1.5. Transferring natural gas by pipelines from the production

source to a distant destination is accomplished by providing multiple pumping sta-

tions connected in series and located at equal distances along the path between the

production source and the receiving reservoir, as shown in Figure IIIc.1.3.

Figure IIIc.1.3. Cross-country pipeline for delivery of natural gas

In each pumping station, gas is compressed and pressurized to compensate for the

frictional losses in the pipeline until the next pumping station. The pressurization

and the cooling of inter-coolers bring pressure and temperature to the values

where gas first enters the pipeline from the production source.

a) Find the pressure drop in the pipeline between the successive pumping stations

and b) find the pumping power for each pumping station for given pipe diameter,

flow rate ( m



), pressure (P

1

), and temperature (T

1

) at the production source.

Data: Natural gas is compressed to P

1

= 120 psia (0.827 MPa), then cooled to the

ambient temperature of T

1

=80 F (26.67 C), as shown in Figure IIIc.1.4. Gas then

enters the pipeline at a velocity of 45 ft/s (13.72 m/s). The pipe has an inside di-

ameter of 2.25 ft (68.6 cm). The pumping stations are located every 15 miles

(24.14 km). Natural gas (considered as methane) molecular weight is 16, its ki-

nematic viscosity at 80 F (26.67 C) is about 2.62E-5 ft

2

/s (2.434E-6 m

2

/s), and γ =

c

p

/c

v

= 1.3.

Figure IIIc.1.4. Pumping stations for pressure recovery

1. Steady Internal Compressible Viscous Flow

411

Solution: a) We assume ideal gas behavior for natural gas, uniform properties at

each cross section, and negligible changes in elevation. We find frictional pres-

sure drop at 15 mile intervals from Equation IIIc.1.19, assuming isothermal flow

in the pipe:

Re = VD/v = 45 × 2.25/2.62E-5 = 3.864E6. Hence, f = 0.184/Re

0.2

= 0.00886 (for

smooth pipe)

c

1

= RT

1

/

2

1

V = (1545/16) × (460 + 80)/(45 × 45/32.2) = 829.15

c

2

= fL/D = 0.00886 × (15 × 5280)/2.25 = 311.87

829.15ȟ – ln ȟ – 517.28 = 0

By iteration (or simply ignoring ln

ξ

) we find

ξ

≈ 0.6233. Hence, P

2

/P

1

=

ξ

1/2

=

(0.6233)

1/2

= 0.7895. Therefore, P

2

= 0.7895(120) = 94.74 psia and ∆P = 120 –

94.74 = 25.26 psi (0.174 MPa).

b) The pumping power is needed to compensate for the unrecoverable pressure

loss over the 15 miles of piping between successive pumping stations. Pumping

power is given be Equation IIIc.1.34 and IIIc.1.35:

»

¼

º

«

¬

ª

−

+−−=

−

)1(

1

)1(

2

1

2

1

γ

rRTr

V

mW

s



where

A =

π

D

2

/4 = 3.14×(2.25)

2

/4 = 3.976 ft

2

(0.369)

R = R

u

/M = 1545/16 = 96.56 ft·lbf/lbmole·R (0.519 kJ/kmol·K)

ρ

1

= P

1

/RT

1

= 144×120/[96.56(460 + 80) = 0.331 lbm/ft

3

(5.3 kg/m

3

)

== AVm

11

ρ



0.331×45 ×3.976 = 59.22 lbm/s (26.86 kg/s)

r = P

3

/P

2

= P

1

/P

2

= 120/94.74 = 1.267

2

20.3/1.3

45 1.3

59.22[ (1 1.267 ) 96.56(460 80)(1.267 1)]

2 32.2 0.3

W =− − + + − =

×



–7.5E5 ft·lbf/s (–1 MW)

B. Flow Rate Measurement of Compressible Fluids

In measuring flow rate of compressible fluids with Bernoulli obstruction meters,

we must take into account the compressibility effect, due to the noticeable change

in the density of the compressible fluid through such devices. The pressure drop

associated with the flow of compressible fluids, especially through a thin-plate ori-

fice, causes the flow to expand adiabatically and density to decrease downstream

of the throat. Our goal is to find an expression similar to Equation IIIb.4.4, that

was derived for the mass flow rate of incompressible fluids. Recall that in the

derivation of Equation IIIb.4.4, which was based on Equation IIIa.3.33, we used

the Bernoulli equation. Here, however, due to the change in the fluid density, we

cannot use the Bernoulli equation. We then start with the energy equation. To

begin the derivation, consider flow through the venturi of Figure IIIb.4.3 where

Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.