Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


IIIc. Fluid Mechanics: Compressible Flow
422
S
S
ρ
ρ
VV
=
where subscript S stands for standard condition. Substituting from Equa-
tion IIIc.2.13, we obtain:
K
2
K
2
K
2V
1
1
11
P
R
T
P
P
T
YA
P
P
RT
YA
PYA
S
s
S
s
S
S
∆
=
∆
=
∆
=
ρρ
ρ
IIIc.2.14
where
ρ
1
is substituted from the ideal gas law. We may further express Equation
IIIc.2.14 in terms of S
g
, the gas specific gravity defined as:
R
R
M
M
S
air
air
g
==
Equation IIIc.12.14 therefore becomes:
K
2V
1
1
P
S
R
T
P
P
T
YA
g
air
S
S
S
∆
=
IIIc.2.15
Example IIIc.2.6. A tank contains carbon dioxide at 113 F (45 C) and 145.1 psia
(1 MPa). The tank is equipped with a 15.28 ft (4.66 m) long, 0.5 in schedule 40
pipe (I.D. = 0.622 in = 15.8 mm). Find the flow rate in standard cubic feet per
minute corresponding to the specified pressure and temperature. (
2
CO
γ
= 1.28
and
2
CO
M = 44).
Solution: We first find the flow rate at the given conditions:
A =
π
D
2
/4 =
π
(0.622/12)
2
/4 = 2.11E-3 ft
2
(1.96E-4 m
2
)
ρ
1
= P
1
/RT
1
= 145.1 × 144/[(1545/44) × (460 + 113)] = 1 lbm/ft
3
(16.6 kg/m
3
)
f = 0.027 (Table IIIb.3.2).
Finding the loss coefficients from Table IIIb.3.3:
K = [L/D + K
Entrance
+ K
Exit
]f = [(15.28 × 12/0.622) + 0.5 + 1] × 0.027 = 8
∆P/P
1
= (145.1 – 14.7)/145.1 = 0.9.
From the table adjacent to Figure IIIc.2.5 for air, the maximum ∆P corresponding
to K = 8 is 0.75. Since the calculated ∆P/P
1
= 0.9 > 0.75, the flow is choked. We
find the net expansions coefficient corresponding to K = 8 as Y = 0.698 and ∆P
max
= 0.762 × 145.1 = 145.86 psi
The volumetric flow rate is found from Equation IIIc.2.15 given S
g
= 44/28.97 =
1.52
S
V
=
8
75.0
97.28/44
97.28/1545
)460113(
1441.145
2.322
1447.14
520
3E11.2698.0 ××
+
×
×
×
×−×
= 0.032 ft
3
/s
2. The Phenomenon of Choked or Critical Flow
423
To expedite arithmetic, we may calculate the constants in Equation IIIc.2.10.
Substituting for A =
π
d
2
/4, R
air
, T
S
, and P
S
, Equation IIIc.2.15 in British Units sim-
plifies to:
()
K
4.678V
1
1
2
P
ST
P
Yd
g
BU
S
∆
=
where d is in inch, P
1
and ∆P in psi, T in degree Rankine, and the volumetric flow
rate is in ft
3
/min.
0.55
0.65
0.70
0.60
0.75
0.80
0.85
0.90
0.95
1.00
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
γ
= 1.3; Cl
2
, CH
4
, C
2
H
2
, C
2
H
4
, CO
2
, H
2
S, H
2
O, NH
3
, N
2
O, SO
2
(P
1
− P
2
)/P
1
1.2
1.5
2
3
4
6
100
40
8
20
10
15
Y
K
K
(P
1
- P
2
)/P
1
Y
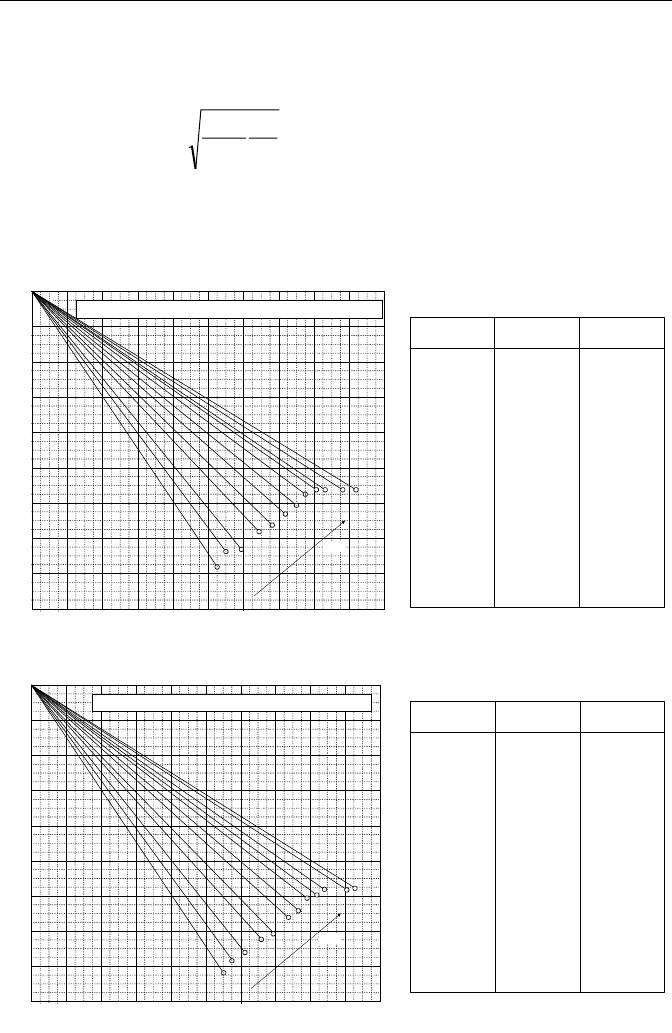
1.2 0.525 0.612
1.5 0.550 0.631
2.0 0.593 0.635
3.0 0.642 0.658
4.0 0.673 0.670
6.0 0.722 0.685
8.0 0.750 0.698
10. 0.773 0.705
15. 0.807 0.718
20. 0.831 0.718
40. 0.877 0.718
100. 0.920 0.718
Limiting Parameters for sonic velocity
(
γ
= 1.3)
0.55
0.65
0.70
0.60
0.75
0.80
0.85
0.90
0.95
1.00
0.00.10.20.30.4 0.5 0.6 0.7 0.8 0.9 1.0
γ
= 1.4; Air, CO, H
2
, HCl, N
2
, NO, O
2
(P
1
− P
2
)/P
1
1.2
1.5
2
3
4
6
100
40
8
20
10
15
Y
K
K
(P
1
- P
2
)/P
1
Y
1.2 0.552 0.588
1.5 0.576 0.606
2.0 0.612 0.622
3.0 0.662 0.639
4.0 0.697 0.649
6.0 0.737 0.671
8.0 0.762 0.685
10. 0.784 0.695
15. 0.818 0.702
20. 0.839 0.710
40. 0.883 0.710
100. 0.926 0.710
Limiting Parameters for sonic velocity
(
γ
= 1.4)
Figure IIIc.2.5. Adiabatic expansion factor for flow of ideal gases for
γ
= 1.3 and 1.4 (Crane)
IIIc. Fluid Mechanics: Compressible Flow
424
2.3. Critical Flow Correlations for Steam
We conclude the single-phase choked flow analysis with presentation of the criti-
cal flow correlations for steam. In this regard, we consider two cases of saturated
and superheated steam.
A. Critical Flow Correlation for Superheated Steam
If steam is superheated, the critical flow can be reasonably found from Equa-
tion IIIc.2.10 so that mass flux is calculated as:
oodBU
TPCG /35.59= IIIc.2.16-1
oodSI
TPCG /31.31= IIIc.2.16-2
where P
o
is in psia (kPa) and T
o
is in degree Rankine (Kelvin) for G to be in
lbm/s·ft
2
(kg/s·m
2
).
However a more accurate relation is:
),v(
25.45
hP
P
CG
dBU
= IIIc.2.17
where P is in psia, specific volume (v) is in ft
3
/lbm, and mass flux (G) is in
lbm/s·ft
2
.
B. Critical Flow Correlations for Saturated Steam
There are several empirical correlations for critical flow of saturated steam. A
correlation that results in reasonable agreement with models such as Moody and
isoenthalpic (as discussed in Chapter Va for two-phase critical flow) is Critco (Na-
havandi 62):
()
185)(
734.13
−
=
Ph
P
G
g
BU
Critco
IIIc.2.18-1
()
28.430)(
726.325
−
=
Ph
P
G
g
SI
Critco
IIIc.2.18-2
where P is in psia (MPa), h
g
in Btu/lbm (kJ/kg), and G in lbm/s·in
2
(kg/s·cm
2
).
Other critical flow correlations for steam include the Napier correlation
(Moody 75):
()
70
P
G
BU
Napier
= IIIc.2.19-1
()
7
P
G
SI
Napier
= IIIc.2.19-2

2. The Phenomenon of Choked or Critical Flow
425
the Grashof correlation (Baumeister):
()
97.0
0165.0 PG
BU
Grashof
= IIIc.2.20-1
()
97.0
0149.0 PG
SI
Grashof
= IIIc.2.20-2
and the Rateau correlation (Baumeister):
()
[]
1000/log96.0367.16
10
PPG
BU
Rateau
−= IIIc.2.21-1
()
[]
100/log96.0292.14
10
PPG
SI
Rateau
−= IIIc.2.21-2
In Equations IIIc.2.19 through IIIc.2.21, P is in psia (MPa) and G is in lbm/s·in
2
(kg/s·cm
2
). As a rough estimate, the critical flow of saturated steam can be
guessed from Napier’s correlation as G
≈ 2P where P is in psia and G is in
lbm/s·ft
2
. Thompson compared the results from Napier’s correlation with data and
observed that the Napier’s correlation overpredicts data between pressures from
100 to 1500 psia and underpredicts data for pressures greater than 1500 psia.
Hence, a pressure correction factor is used for this correlation for the source pres-
sure in the range of 1500 < P < 3200 psia as follows:
10612292.0
10001906.0
−
−
=
P
P
C
Napier
IIIc.2.22
where P is in psia. The ASME Boiler and Pressure Vessel Code uses the Napier’s
correlation with the above correction factor. The choked flow rate is then calcu-
lated from:
()
70/9.0
max
PACCm
cNapierd
=
IIIc.2.23
where mass flow rate is in lbm/s, A
c
is the choking area in square inch, P is in psia,
and C
d
is the discharge coefficient.
Example IIIc.2.7. Saturated steam at 1000 psia (6.89476 MPa) is discharged to
the atmosphere through a 1/8 in (3.175 mm) diameter valve. Find mass flow rate
of steam.
Solution: Since flow of steam discharged from 1000 psia to 14.7 psia is choked,
we may use Critco or other correlations IIIc.2.19 through IIIc.2.21. For Critco, h
= h
g
= 1192.9 Btu/lbm (2774.5 kJ/kg):
G
Critco
= 13.734×1000/(1192.9 –185) = 13.63 lbm/s·in
2
(0.958 kg/s·cm
2
)
G
Napier
= 1000/70 = 14.28 lbm/s·in
2
(1 kg/s·cm
2
)
G
Grashof
= 0.0165(1000)
0.97
= 13.41 lbm/s·in
2
(0.943 kg/s·cm
2
)
G
Rateau
= [16.267 – 0.92(2.158 + log
10
1000)] = 13.48 lbm/s·in
2
(0.948 kg/s·cm
2
)
G
rough estimate
= 2 × 1000 = 2000 lbm/s·ft
2
= 13.88 lbm/s·in
2
(0.976 kg/s·cm
2
)
Note that Napier’s correlation has predicted the largest choked flow rate.
IIIc. Fluid Mechanics: Compressible Flow
426
Example IIIc.2.8. A pressure vessel is filled with air. A small valve is opened to
vent the vessel. Find the vessel pressure after 15 s. The mass flow rate through
the valve is given as TbPm
e
/=
. In BU;
e
m
in lbm/s, P in psia, and T in R,
the value of b is given as b = 0.5148 lbm·ft
2
·R
1/2
/(s·lbf). Other data are as follows;
P
1
= 1000 psia, T
1
= 150 F, V = 100 ft
3
, d
Valve
= 1 inch, A
Valve
= 5.454× 10
-3
ft
2
,
(C
d
)
Valve
= 0.65.
Solution: We must solve the conservation equations for mass and energy as well
as the volume constraint simultaneously. The involved equations constitute a set
of first-order non-linear differential equations, thus we use a finite difference ap-
proach. The FORTRAN program used to solve this problem is included on the
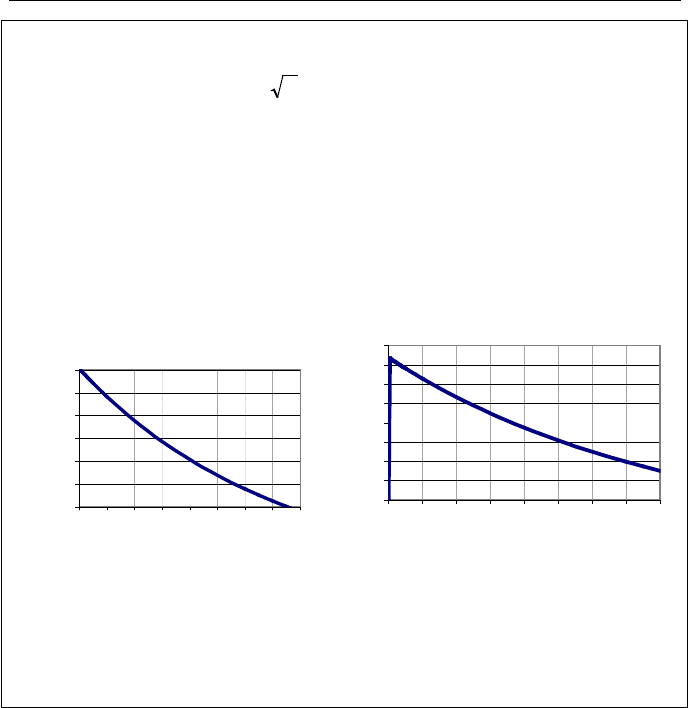
accompanying CD-ROM and is the same that was used to solve Example IIa.8.7.
The results for pressure and mass flow rate are plotted versus time.
400
500
600
700
800
900
1000
0246810121416
Time (s)
Gas Pressure (psia)
6
8
10
12
14
16
18
20
22
0 2 4 6 8 10121416
Time (s)
Gas Mass Flow Rate (lbm/s)
From the pressure plot versus time, we find P(t = 15 s) = 400 psia. Discharging
pressurized vessels results in a rapid drop of the gas temperature. Thus, pressure
vessels undergoing rapid discharge should be designed to withstand high thermal
stresses. Also, note that in this problem we ignored any heat transfer to or from
the tank structure. If the tank is poorly insulated, the rate of heat transfer should
be included in the formulation.
QUESTIONS
− How does pressure drop calculation of compressible fluids differ from incom-
pressible fluids?
− What manipulation do you use to express Equation IIIb.3.7 in terms of the Ma
number?
− Why is it a reasonable assumption for friction factor to remain constant in the
isothermal flow in pipes?
− Is Equation IIIc.1.19 applicable to the flow of compressible fluids in any pipe
length?
− Why does the subsonic flow accelerate?
− Is it correct to say that in supersonic flow, pressure actually increases in the
flow direction?
− Why is a maximum pipe length calculated for the flow of compressible fluids in
pipes?

Questions and Problems
427
− Why do we have to define the adiabatic expansion factor for the flow of com-
pressible fluids?
− What is the value of the adiabatic expansion factor for incompressible fluids?
− What is the value of Y for CO
2
flowing through an orifice with D
throat
= D
pipe
/2?
− What is the critical or choked flow?
− When does flow become choked?
− Is choked flow associated only with the flow of the compressible fluids?
− What is the critical pressure? What happens when the back pressure is less
than, equal to or greater than the critical pressure?
− What is the critical pressure of air at a stagnation pressure of 2 MPa?
− Why is flow choked if we cannot find Y from the plots of Figure IIIc.2.5?
PROBLEMS
1. Consider the flow of a compressible fluid in a conduit under steady state and iso-
thermal conditions. The flow density changes from point a to point b that is located
downstream of point a. Compare the flow Reynolds number at these points and
specify whether Re
a
> Re
b
, Re
a
= Re
b
, or Re
a
< Re
b
.
2. Air at pressure P
1
, temperature T
1
, and mass flow rate of m
enters a compressor.
Air pressure rise over the compressor is
∆P
1
. Water at the same conditions enters a
pump and its pressure is raised by the same amount. Compare the required pumping
powers for air,
a
W
and for water,
w
W
.
[Hint.
ρ
/V mPPW
∆=∆= ].
3. Use Equation IIIc.1.14 to show that:
¸
¹
·
¨
©
§
−
−+
+
¸
¹
·
¨
©
§
−
−+
−
¸
¸
¹
·
¨
¨
©
§
−
+
=
RT
dF
A
dA
a
Tc
dq
d
p
2
2
2
2
2
2
2
2
Ma1
Ma)1(2
M1
Ma)1(2
Ma1
Ma1
Ma
Ma
γγ
γ
Use this result and substitute for dF/RT term to directly derive Equation IIIc.1.30 for
the adiabatic flow of compressible fluids in constant flow area channels.
4. Methane at a rate of 1 kg/s is flowing inside a pipeline. The pipe inside diameter
is 1 m. Find the Ma number at a location where pressure and temperature are meas-
ured as 1 MPa and 27 C, respectively. M
CH4
= 16.043,
γ
CH4
= 1.304. [Ans.: 0.44].
5. Carbon dioxide is flowing in a conduit at 50 psia, 100 F, and a velocity of 50 ft/s.
Find the flow Ma number at this location. M
CO2
= 44.01,
γ
CO2
= 1.28. [Ans.: 0.056].
6. Air enters a duct at 700 kPa and Ma = 0.05. The duct has a wetted perimeter of 1
m and a flow area of 0.1 m
2
. Find the air pressure at a length of 150 m from the pipe
entrance. The air temperature remains constant in the pipe.
7. Air flows in a pipeline at a rate of 25 kg/s. The pipe is 1000 m long and has an
inside diameter of 0.35 m. Assuming isothermal process, find the pipe length over
which the flow remains subsonic. Data: P
i
= 0.5 MPa, T
i
= 27 C, f = 0.015.
IIIc. Fluid Mechanics: Compressible Flow
428
8. Compressed air in a facility. For this purpose, a compressor delivers 1 lbm/s of
air in a 2 in schedule 40 pipe at 50 psia and 80 F. Assuming the flow is isothermal,
find the length of the pipe at the end of which flow becomes sonic.
9. Natural gas is flowing in a pipeline of 2.5 m diameter at a rate of 100 kg/s. The
pipeline is well insulated. The gas at the exit of the pumping station’s compressor
has a pressure of 700 kPa and a temperature of 40 C. Find the maximum pipe length
for continuous flow.
10. Air enters a pipe at a Mach number of 0.1. The pipe is 1000 m long, having an
inside diameter of 0.25 m. The flow is isothermal and the friction factor remains
constant over the entire length of the pipe at 0.013. Find the Mach number at the
exit of the pipe.
11. Natural gas, compressed to P
1
= 100 psia then cooled to T
1
= 70 F, flows in a
cross-country pipeline at a velocity of 40 ft/s. The pipe is smooth and has an inside
diameter of 2 ft. To maintain pressure, pumping stations are established every 10
miles along the route. In each pumping station, natural gas is compressed to its
original pressure and cooled to its original temperature. Find the pressure drop be-
tween each pumping station and the required pumping power. Assume natural gas
as pure methane with k = 1.3, molecular weight of 16 and kinematic viscosity of
2.61E-5 ft
2
/s.
[Ans.: Re = 0.31E7, f = 0.00928, P
2
= 87.29, c
2
= 264, ∆P = 12.71 psi,
m
= 35.36 lbm/s, Ma = 0.03, and W
= 454 hp].
12. Show that in an isentropic process involving flow in a horizontal flow path, vdP
+ VdV = 0.
13. Show that
()
s
critical
ddPG v/−= .
14. A tank contains air at stagnation properties of 200 kPa and 30 C. A vent of 3
cm diameter is opened. a) Find air flow rate if P
b
= 150 kPa and b) if P
b
= 101.35
kPa. [Ans.: For C
d
= 1, a) 0.29 and b) 0.33 kg/s].
15. Air in an isentropic process and at a rate of 6 kg/s is expanded through the throat
to an exit Mach number of 3. The air pressure and temperature at the inlet of are P
o
= 300 kPa and T
o
= 300 C, respectively. Find a) the throat area, b) the air pressure
and temperature at the exit, c) exit velocity and area.
16. Air in an isentropic process and at P
o
= 250 kPa and T
o
= 600 K is expanded
through the throat to an exit Mach number of 2.5. The throat diameter is 11 cm.
Find a) the mass flow rate of air, b) the air pressure and temperature at the exit, c)
exit velocity and area.
17. A fully inflated tire has a volume of 15 ft
3
. The pressure and temperature of the
air in the tire are 65 psia and 75 F, respectively. At this condition, the air intake
needle is depressed for 3 s and then released. Treating air as an ideal gas and assum-
ing small changes in the tire temperature and volume, Find the amount of air that left
the tire. Assume a discharge coefficient of 0.61 and a flow area of 0.01 in
2
.

Questions and Problems
429
18. Air flows steadily from a high pressure container (A) to a low pressure con-
tainer (B) through an ideal convergent-divergent nozzle. Find the flow area at the
throat and at the exit of the nozzle. Data: mass flow rate: 2 kg, air pressure in con-
tainer A: 700 kPa, inlet temperature: 116 C, air pressure in container B: 70 kPa.
19. A tank contains carbon dioxide maintained at 50 C and 0.5 MPa. The tank is
equipped with a 4.5 m long pipe. The pipe has in inside diameter of 1 cm. Find the
flow rate in standard cubic feet per minute corresponding to the specified pressure
and temperature. (
2
CO
γ
= 1.28 and
2
CO
M = 44).
20. In a repair shop compressed air is used to operate pneumatic tools. The total
length of the airline including all the loss coefficients in terms of equivalent length is
about 152.5 m (500 ft). The airline consists of smooth pipe of I.D. = 1.27 cm. Air is
compressed to 0.345 MPa (50 psia) and then cooled to 24 C (75 F) when entering
the line at a velocity of 2.4 m/s (8 ft/s). Find pressure when air is used to operate the
pneumatic tool.
To Pneumatic tool
Air
intake
Compressor
21. In a repair shop compressed air is used to operate pneumatic tools. The total
length of the airline including all the loss coefficients in terms of equivalent air is
about 500 ft. The airline consists of smooth pipe of I.D. = 0.5 inch. The com-
pressed air is cooled to 75 F when entering the line. A pneumatic tool requires 35
psia of compressed air to operate. To what pressure should the air be pressurized by
a compressor to provide the desired pressure for the tool? What power is required to
obtain such pressure if the compression process can be assumed isentropic? Air ve-
locity at the inlet is 10 ft/s.
22. A fully inflated tire has a volume of 15 ft
3
. The pressure and temperature of the
air in the tire are 65 psia and 75 F, respectively. At this condition, the air intake
needle is depressed for 5 seconds. Treating air as an ideal gas and assuming small
changes in the tire temperature and volume, plot the mass flow rate of air versus
time. Assume a discharge coefficient of 0.61 and a flow area of 0.01 in
2
.
23. Find the value of the adiabatic expansion factor, Y for CO
2
flowing through an
orifice with
β
= 0.5 and r = P
2
/P
1
= 0.85. [Ans.: 0.95]
24. A PWR plant is equipped with atmospheric dump valves (ADV) and turbine
bypass valves (TBV). The role of an ADV, installed on the steam line, is to dump
steam to the atmosphere in case of a plant trip, while the role of the TBV is to diert
steam to the condenser in the case of a turbine trip. The specification sheet as pro-
vided by the manufacturer specifies flow rates of 292,500 lbm/h and 1,173,000

IIIc. Fluid Mechanics: Compressible Flow
430
lbm/h at the saturation temperature of 556 F for the ADV and the TBV, respectively.
Assuming a C
d
of 0.61 for both valves find the ADV and the TBV effective flow ar-
eas. [Ans.: 8.87 in
2
and 35.58 in
2
].
25. Air flows through a nozzle with differential pressure taps located at D: D/2 up-
stream and downstream, respectively. For this nozzle, D
throat
= 0.75D
pipe
. What is
the value of Y if r = 0.85?
26. A tank containing air is pressurized to 1.7 MPa and 30 C. A valve is now
opened to discharge air to the atmosphere through a flow area of 6.45 cm
2
. Find the
maximum flow rate. [Ans.: 372 kg/s].
27. Compare Critco, Napier, Grashof, and Rateau critical flow correlations for the
range of 50 – 2500 psia.
28. The steam generator of a PWR is operating at 6.55 MPa (950 psia). Due to a
sudden plant trip, the atmospheric dump valve opens (ADV) to discharge steam.
Find the steam flow rate through the ADV. The valve flow area is 40.88 cm
2
(0.044
ft
2
). The valve discharge coefficient is 0.61.
29. A pressure vessel is filled with pressurized saturated steam. A small valve is
opened to vent the vessel. Find the vessel pressure after 30 s. Data: P
1
= 1000 psia,
V = 100 ft
3
, D
Valve
= 1 inch, (C
d
)
Valve
= 0.65.
30. A pipe carrying a high pressure air rupturs inside a compartment. The com-
partment has a vent to discharge air to the atmosphere. Assuming steady state con-
dition, derive an algorithm for the calculation of peak pressure in the compartment.
Compartment
High Energy Line Break
Vent
[Hint: Assuming an isothermal process, the compartment pressure keeps rising as
long as the flow rate from the broken pipe exceeds the flow through the vent. The
compartment pressure peaks when these flow rates become equal. Apply a dis-
charge coefficient to Equation IIIc.2.9 and set the result equal to Equation IIIc.2.10].
31. A high energy pipe, carrying nitrogen ruptures inside a compartment. Use the
given data to find the peak pressure reached in the compartment following the event.
Treat nitrogen as air. Data: Nitrogen pressure is 1600 psia (11 MPa), room and ni-
trogen are at the same initial temperature of 75 F (24 C), diameter of the pipe is 10
in (25.4 cm) and the vent flow area of the compartment is 120 ft
2
(11 m
2
).
IV. Heat Transfer
The processes that a given control volume may go through were discussed in
chapters on thermodynamics and fluid flow. We showed that to find the condi-
tions at the end of a process, given specified conditions at the beginning of the
process, we should use the conservation equations of mass, momentum, and en-
ergy in conjunction with the equation of state. In most cases, the rate of heat
transfer to or from a control volume is not known, thus it must be determined from
a constitutive relation. The topic of heat transfer helps us identify the applicable
mode of heat transfer and provides us with the constitutive relation, which corre-
lates temperature to the rate of heat transfer.
There are three modes of heat transfer; conduction, convection, and radiation.
Conduction is more pronounced in solids and stems from molecular diffusion due
to an existing temperature gradient. The radiation mechanism is less understood.
In certain conditions, radiation can be explained according to wave mechanics and
in other situations according to quantum mechanics. Radiation heat transfer ap-
plies to solids, liquids, and gases. On the other hand, convection is solely due to
the bulk motion of a fluid, transferring heat in the process. As such, convection
heat transfer is pertinent only to fluids. Convection heat transfer is the dominant
mode not only in single-phase but also in two-phase flow such as heat transfer as-
sociated with phase change in boiling and condensation. As discussed in Chap-
ter I, the constitutive relation in heat conduction, heat convection, and thermal
radiation is known as Fourier’s law, Newton’s law of cooling, and the Stefan-
Blotzmann law, respectively.
IVa. Conduction
The goal of studying conduction heat transfer is to determine the temperature dis-
tribution within a substance and the rate of heat transfer to or from the substance.
The entire topic of conduction heat transfer is based on the energy equation as de-
rived in Chapter III. Fortunately, in conduction heat transfer, the energy equation
can be significantly simplified due to the absence of such terms as the rate of work
performed by pressure forces and the rate of work performed by viscous forces.
In most cases, change in stagnation energy due to convection is also absent. As
shown later in this chapter, the elimination of these terms allows the use of ana-
lytical solutions in closed form for certain classes of problems.
In this chapter, following the introduction of pertinent terms, we first derive the
heat conduction equation in its general form. We then discuss the concept of
lumped parameter versus one-, two-, or three-dimensional analysis. The primary
