Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


482 IVa. Heat Transfer: Conduction
)()'()'()(
)()'()()'(
)
4
(
)(
0110
1111
bb
bb
fbb
mrKmrImrKmrI
mrImrKmrKmrI
TThkr
Q
+
+
=
−
π
δ
IVa.8.5
Example IVa.8.1. Find temperature in an annular fin at r = 6 in. Data: k = 10
Btu/h·ft·F, T
b
= 400 F, T
f
= 65 F, h = 50 Btu/h·ft
2
·F, r
b
= 5 in, r
t
= 9 in and
δ
= 0.25
in. Also find the total rate of heat transfer.
Solution: We use Equations IVa.8.4 to find T and Equation IVa.8.5 to find the
rate of heat transfer. We first find m = [50/(10 × 0.25/12)]
0.5
= 15.5 ft
-1
and then
r’ = r
t
+
δ
= 9 + 0.25 = 9.25 in so that mr’ = 11.95 and mr
b
= 6.46. We find the
following Bessel functions:
Argument I
o
I
1
K
o
K
1
mr
b
= 6.46 0.254 –0.165 0.758E-3 0.814E-3
mr = 7.75 0.225 – 0.192E-3 –
mr’ = 11.95 – 0.226 – 0.241E-5
T =
3E758.0226.05E241.0254.0
225.05E241.03E192.0225.0
)65400(65
−×+−×
×−+−×
−+
= 150.6 F
Similarly, for total rate of heat transfer we have:
Q
=
3E758.0226.05E241.0254.0
5E241.0165.03E814.0226.0
)/4)(65400(12/25.01050)12/5(
−×+−×
−×−−×
−××
π
=
612.5 Btu/h
Without the fin, Q
= 2
π
r
b
× 2
δ
(T
b
– T
f
) = 2
π
(5/12)(2 × 0.25/12)(400 – 65) =
36.54 Btu/h.
Case 3: Fins with Constant Heat Diffusion Area. Examples of such fins in-
clude longitudinal fins of rectangular profile and cylindrical spines as shown in
Figure IVa.8.6. Since the conduction area is constant alongside the fin, the second
term in Equation IVa.8.1 is zero and this equation simplifies to:
0)(
P)(
2
2
=− x
k
h
A
dx
xd
θ
θ
In the case of a fin with a rectangular profile, the perimeter is P = 2(b + 2
δ
) and
the heat diffusion area is A = 2b
δ
. In the case of cylindrical spines P = 2
πδ
and
heat diffusion area is A =
πδ
2
. Therefore, m
2
for the fin with rectangular profile is
given as:
k
h
kb
hb
m
δδ
δ
≅
+
=
)2(
2
rrectangula
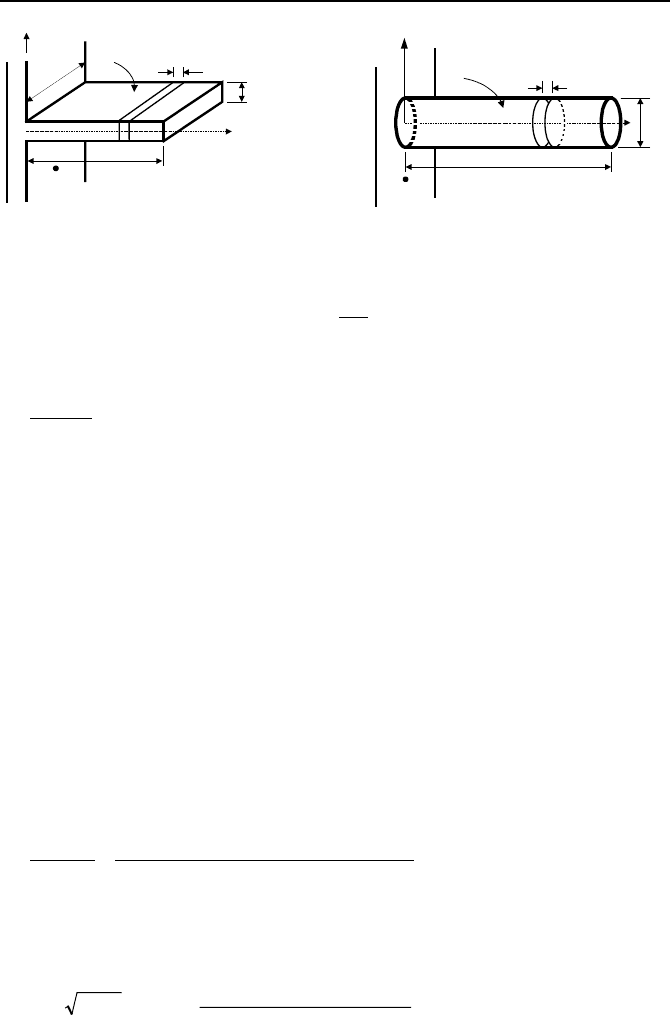
8. Analytical Solution of Heat Conduction Equation, Extended Surfaces 483
L
b
dx
2
δ
x
y
h , T
f
T
b
dx
L
2
δ
x
h , T
f
T
b
y
Figure IVa.8.6. Longitudinal fin of rectangular profile and cylindrical spine
and for cylindrical spines as
k
h
m
δ
2
2
cylinder
= . Hence, the governing equation for
such fins becomes:
0)(
)(
2
2
2
=− xm
dx
xd
θ
θ
IVa.8.6
The general solution for Equation IVa.8.6 is given in Chapter VIIb as
mxmx
ecec
21
+=
−
θ
. Coefficients c
1
and c
2
can be found from the boundary con-
ditions at the base, x = 0 and at the tip, x = L. At the base, the temperature must
be equal to the specified base temperature of T = T
b
. At the tip, three types of
boundary conditions can be specified as follows.
BC, Type 1: the tip of the fin is insulated, hence –k dT(L)/dx = 0.
BC, Type 2: fin is so long that heat transfer through convection has caused tip
temperature to reach T
f
.
BC, Type 3: the tip of the fin is also losing heat to the environment by convec-
tion, -kdT(L)/dx – hA(T-T
f
) = 0.
The solution for types 1 and 2 is left to the reader. As was discussed in Case 2, we
can reduce type 3 to type 1. However, this case is much simpler than the annular
fin and we can treat it with a convection boundary at the tip. The solution for tem-
perature distribution in the fin for type 3 boundary condition is:
mLkmhmL
xLmkmhxLm
TT
TT
fb
f
sinh)/(cosh
)(sinh)/()(cosh
+
−+−
=
−
−
IVa.8.7
Having the temperature profile, we can find total rate of the fin heat loss from
0
)/(
=
−=
x
dxdTkQ
:
mLkmhmL
mLkmhmL
TTkAhQ
fb
sinh)/(cosh
cosh)/(sinh
)(P
+
+
−=
IVa.8.8
484 IVa. Heat Transfer: Conduction
8.2. 1-D S-S Heat Conduction in Fins ( 0≠
′′′
q
)
If nuclear fuel rods are equipped with fins, an internal heat generation can take
place in the fin due to the bombardment by
γ
radiation as discussed in Sec-
tion IVa.5.5. Assuming such internal heat generation is uniform, Equation IVa.8.1
should then include an additional term to have:
k
q
x
k
h
xAdx
xd
dx
xdA
xA
dx
xd
′′′
−=−+
)(
)(
P)(
]
)(
)(
1
[
)(
2
2
θ
θθ
IVa.8.9
Therefore, the general solution we obtained for various fin profiles is also applica-
ble to the case that such fins have internal heat generation. However, the specific
solution must also be found due to the addition of the constant term in the right
side of Equation IVa.8.9 as explained next.
Case 1. Annular fin with internal heat generation. The governing equation is:
k
q
m
dr
d
r
dr
d
′′′
−=−+
θ
θθ
2
2
2
1
IVa.8.10
and the solution is given by El-Wakil is:
)()'()'()(
)()'()()'(
)1(
0110
0101
bb
gg
fb
f
mrKmrImrKmrI
mrImrKmrKmrI
RR
TT
TT
+
+
−+=
−
−
IVa.8.11
where I and K are the modified Bessel functions of the first and second kind. The
rate of heat transfer from the fin from the base material is found from:
)()'()'()(
)()'()()'(
)
4
)(1(
)(
0110
1111
bb
bb
g
fbb
mrKmrImrKmrI
mrImrKmrKmrI
R
TThkr
Q
+
+
−=
−
π
δ
IVa.8.12
where R
g
in these equations is a dimensionless number known as the generation
ratio and is given by:
)(
2
fb
g
TTkm
q
R
−
′′′
=
Case 2: Fins with Constant Heat Diffusion Area and Internal Heat Generation.
Here, the governing equation simplifies to:
k
q
xm
dx
xd
′′′
−=−
)(
)(
2
2
2
θ
θ
IVa.8.13
To find the solution, we use the insulated tip boundary condition by extending the
length in Figure IVa.8.6 by
δ
+= LL' , resulting in:

9. Analytical Solution of Transient Heat Conduction 485
'cosh
)'(cosh
)1(
mL
xLm
RR
TT
TT
gg
fb
f
−
−+=
−
−
IVa.8.14
The rate of heat transfer dissipated from the fin (from the base material) obtained
by using Fourier’s law
Q
= – kAdT/dx. Taking the derivative of temperature pro-
file and substituting, we find:
'tanh)()1( mLTTmkARQ
fbg
−−=
IVa.8.15
where
δ
bA =
rrectangula
and
πδ
2=
cylinder
A . If there is no internal heat genera-
tion, R
g
= 0.
The analytical solution to the two-dimensional heat conduction equation at
steady state condition is discussed in Section IVa.9.2. It is demonstrated that a
product solution in the form of T(x, y) = X(x)Y(y) can be found for the Laplace
equation
∂
2
T/∂x
2
+ ∂
2
T/∂y
2
= 0.
9. Analytical Solution of Transient Heat Conduction
We can find analytical solutions to transient heat conduction for two types of one-
dimensional problems. The first type includes the so-called semi-infinite solids.
The second type includes solids having familiar geometries such as slab, cylinder,
and sphere. Both types of problems are discussed in this section.
9.1. 1-D Transient Heat Conduction, Semi-infinite Solid
An interesting application of one-dimensional transient heat conduction is in find-
ing the response of semi-infinite objects to sudden imposition of various boundary
conditions at the surface. Although the semi-infinite solid is a mathematical con-
cept, it can be used in many practical applications. Considering buried pipelines
carrying water for example, we are interested in knowing the penetration depth of
sudden freeze on the ground. This would determine how deep a water main
should be buried for protection from freeze rupture. The ground can then be
treated as a semi-infinite solid. The reason we are able to find an analytical solu-
tion is that we treat ground, where the pipe is buried, to be infinite in the y and z
directions (
∞<<−∞ y and ∞<<−∞
z
) and semi-infinite only in the x-direction
(
∞<≤ x0 ) as shown in Figure IVa.9.1. The semi-infinite model implies that
temperature deep inside the solid remains unaffected by the changes in tempera-
ture at the surface. This is used as a boundary condition. The governing equation
for a semi-infinite solid is the 1-D form of Equation IVa.2.3 in the x-direction:
t
T
x
T
∂
∂
=
∂
∂
2
2
α
IVa.2.3

486 IVa. Heat Transfer: Conduction
x
y
z
x
x
T
i
x
T
i
T
i
T
S
h , T
f
x
T
x
T
x
T
T
i
T
S
T
i
T
i
T
f
ttt
∞
∞
∞
∞
∞
∞
s
q
′′
Figure IVa.9.1. Imposition of various boundary conditions at the surface of a semi-infinite
solid
The solution requires two boundary conditions and one initial condition. The
initial condition is the uniform temperature of the solid before the imposition of
any instantaneous change at its surface, T(x,0) = T
i
. One boundary condition deals
with the heat transfer mechanism at the surface and the other deals with the fact
that, far away from the surface, the temperature remains at its initial value,
i
TtT =∞ ),( . The heat transfer mechanism at the surface is either in the form of
imposition of an instantaneous temperature, or instantaneous exposure to either a
heat flux or a convection boundary. We will use these three types of boundary
conditions in three Cases A, B, and C as discussed below. For now, we try to find
a solution to the 1-D form of Equation IVa.2.3. Among the several methods to
solve this equation, one deals with the integral technique where a profile for tem-
perature distribution is assumed. The coefficients are then found by setting the to-
tal rate of heat transfer equal to the rate of heat transfer at the surface. Another
method is to use the Laplace transform. The approach discussed here uses the
transformation of variables method.
Our goal is to find a single variable such as s = f(x, t) so that we can express
temperature only in terms of s rather than both x and t. We choose the function
f(x, t) as s = x/g(t). At x = 0 and any t, variable s also becomes zero and at t = 0
and any x, variable s also becomes infinity. The latter constraint would represent
the entire solid and will be used as an initial condition. Therefore, the goal is now
to find the unknown function g(t). Keeping this goal in mind, we will try to ex-
press temperature in Equation IVa.2.3 in terms of s. To do this, we need to find
out the partial derivative of temperature with respect to x and t. The first deriva-
tive is found as:
s
T
tgx
s
s
T
x
T
∂
∂
=
∂
∂
∂
∂
=
∂
∂
)(
1
and the second derivative as:
2
2
22
2
2
2
)(
1
][
)(
1
]
)(
1
[
x
T
tg
x
s
s
T
tgs
T
tgx
x
T
∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
IVa.9.1
9. Analytical Solution of Transient Heat Conduction 487
Having defined the left side of Equation IVa.2.3 in terms of g(t), we now seek to
express the temperature derivative with respect to time (i.e., the right side of Equa-
tion IVa.2.3) in terms of the temperature derivative with respect to
s:
]
)(
)(
1
][[]
)(
)(
][[
2
dt
tdg
tg
s
s
T
dt
tdg
tg
x
s
T
t
s
s
T
t
T
−
∂
∂
=−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
IVa.9.2
We can now substitute Equations IVa.9.1 and Equation IVa.9.2 into Equation
IVa.2.3 to obtain:
0]
)(
)(
4
2
[2
2
2
=+
dt
tdg
tg
ds
dT
s
ds
Td
α
IVa.9.3
Our goal of finding g(t) to express temperature in terms of s = x/g(t), is now re-
duced to finding g(t) so that the bracket in Equation IVa.9.3 becomes equal to
unity;
1
)(
)(
4
2
=
dt
tdg
tg
α
This is a first order linear differential equation from which, g(t) can be found as
ttg
α
2)( = . Having found g(t) and consequently the variable s as txs
α
2/= ,
we now return to Equation IVa.9.3 to find a solution for the second-order linear
differential equation:
s
dsd
T
dsTd
2
/
/
22
−=
This equation can be integrated to obtain:
1
2
ln)/ln( csdsdT +−= IVa.9.4
where
c
1
is the constant of integration and is conveniently chosen as a logarithmic
term. Equation IVa.9.4 can be written as:
dT/ds = c
1
exp(-s
2
) IVa.9.5
which, upon integration
, gives temperature distribution in the semi-infinite solid.
To find the constants of integration, we need to use the boundary and initial condi-
tions. There are generally three types of boundary conditions specified at the sur-
face. These are discussed below as Cases 1, 2, and 3.
Case 1. Imposition of an instantaneous temperature at the surface. In this
case, we investigate the response of a semi-infinite solid to a sudden change of
temperature at its surface. To determine temperature, we integrate Equa-
tion IVa.9.5 from zero to any
s:

488 IVa. Heat Transfer: Conduction
³³
−
=−=
s
s
s
dsecTsTds
ds
dT
0
1
0
2
)0()(
where T(s = 0) = T(0, t) = T
S
where T
S
is the temperature of the semi-infinite
solid at its surface. To find constant c
1
, we use the initial condition at t = 0 and
any x. This implies that as
∞→
s
, T(s) = T
i
. Therefore;
³
∞
−
=−
0
1
2
)0( dsecTT
s
i
IVa.9.6
as is shown in Section 3 of Chapter VIIb,
2/
0
2
π
=
³
∞
−
dse
s
. By substituting
into Equation IVa.9.6, we conclude that
π
/)]0([2
1
TTc
i
−= . Thus, the tem-
perature distribution in the semi-infinite body becomes:
³
−
=
−
−
s
s
Si
S
dse
TT
TtxT
0
2
2
),(
π
IVa.9.7
Therefore, we successfully managed to find the temperature distribution in a semi-
infinite solid subject to an instantaneous change of temperature from T
i
to T
S
at its
surface. The following integral is known as the Gaussian error function and is
plotted in Figure IVa.9.3.
Error function:
³
−
s
s
dse
0
2
2
π
IVa.9.8
The penetration of the surface disturbance at any distance
x from the surface at
any time
t is given by:
S(x, t) =
)
2
(
),(
t
x
erf
TT
TtxT
Si
S
α
=
−
−
IVa..9.9
To find the heat flux at the surface, we use Leibnitz’s rule (Equation VIIc.1.26) to
carryout differentiation of an integral. Note that in this case, the first and the last
terms in the right side of Equation VIIc.1.26 are zero. Hence, the surface heat flux
is found as:
()
t
TTk
t
x
x
eTTk
x
T
kq
iS
t
x
SiS
πααπ
α
)(
2
2
4
2
−
=
¸
¸
¹
·
¨
¨
©
§
∂
∂
−−=
∂
∂
−=
′′
−
IVa.9.10
Example IVa.9.1. The surface temperature of a large aluminum slab is suddenly
raised and maintained at 135 C. The slab is originally at a uniform temperature of
30 C. Find the temperature at a depth of 20 cm and the surface heat flux 10 min
after the event. Aluminum properties: k = 204 W/m·C and
α
= 8.42E-5 m
2
/s.

9. Analytical Solution of Transient Heat Conduction 489
Solution: We first find the argument (arg) then the related function as follows:
arg = x/2(
α
t)
0.5
= 0.2/2(8.42E-5 × 600)
0.5
= 0.44 and the corresponding value is
erf(0.44) = 0.466
T = T
s
+ (T
i
– T
s
)erf(0.44) = 135 + (30 – 135) × 0.466 = 86 C
()
tTTkq
iS
πα
/−=
′′
= 204(135 – 30)/(
π
× 8.42E-5 × 600)
1/2
= 53.77 kW
Case 2. Imposition of an instantaneous heat flux at the surface. At any time,
the temperature of any point within a semi-infinite solid, the surface of which is
exposed to an instantaneous and uniform heat flux, is obtained from:
S(x, t) =
)
2
()
4
exp(
/2
2
t
x
erfc
k
q
t
x
k
tq
TT
S
S
i
α
α
πα
′′
−
−
′′
=−
IVa.9.11
where the complementary error function is defined as erfc(x) = 1 – erf(x).
Case 3. Imposition of an instantaneous convection at the surface. In this case,
the transient is a result of exposing the surface of a semi-infinite solid to convec-
tion heat transfer. The objective is to determine the penetration of convection
temperature into the solid at a given time. The solution to this problem is
given as:
S(x, t)
=
¸
¸
¹
·
¨
¨
©
§
+×
¸
¸
¹
·
¨
¨
©
§
+−
¸
¸
¹
·
¨
¨
©
§
=
−
−
k
th
t
x
erfc
k
th
k
hx
t
x
erf
TT
TT
fi
f
α
α
α
α
2
exp
2
2
2
IVa.9.12
Example IVa.9.2. The surface of a large steel slab is suddenly cooled with flow-
ing air. Find temperature at a depth of 15 in, 1 hour after exposure to the cold air
at the surface. Steel properties: k = 25 Btu/ft·h·F and
α
= 1.3E-4 ft
2
/s. Air flows
at T
f
= 65 F and h = 10 Btu/ft·h·F. Initial steel temperature is 850 F.
Solution: We first find the arguments then the values of the corresponding error
functions:
arg
1
= x/2(
α
t)
0.5
= (15/12)/2(1.3E-4 × 3600)
0.5
= 0.914,
erf(arg
1
) = 0.804
arg
2
= hx/k + h
2
α
t/k
2
= 10 × (15/12)/25 + 100 × 1.3E-4 × 3600/625 = 0.575,
exp(arg
2
) = 1.78
arg
3
= arg
1
+ h(at)
0.5
/k = 0.914 + 10 × (1.3E-4 × 3600)
0.5
/25 = 1.187,
erfc(arg
3
) = 0.093
S(x, t) = =
−
−
65850
65T
[0.804 – 1.78 × 0.093] = 0.6385
Therefore, temperature at x = 15 in is found as:
T – T
f
= (T
i
– T
f
) × S(x,t). Substituting, T = 65 + (850 – 65) × 0.6385= 566 F.

490 IVa. Heat Transfer: Conduction
Now that we have dealt with three types of boundary conditions for a semi-
infinite solid, we will discuss two interesting aspects. First, we consider two semi-
infinite solids brought in contact. Second, we analyze the response of a semi-
infinite solid to a harmonically oscillating temperature boundary condition.
9.2. Semi-infinite Bodies in Contact
Experience shows that we can sense the relative temperature of various objects in
a room by touching. While counterintuitive, we can explain this phenomena by
treating our hand and the object we touch as semi-infinite solids in contact. Each
semi-infinite solid is originally at uniform temperature, for example T
i,1
and T
i,2
,
respectively. When these solids are brought in perfect contact (Figure IVa.9.2),
the interface must satisfy two boundary conditions for each solid. First, both sol-
ids must have the same temperature at the interface. Second, the heat flux leaving
the warmer solid must be equal to the heat flux entering the colder solid. The as-
sumption of perfect contact allows us to use a zero thermal resistance at the inter-
face.
T
2
(x, t)
Interface
T
2, i
T
1
(x, t)
T
1, i
k
1
,
α
1
k
2
,
α
2
T
2
(x, t)
Interface
T
2, i
T
1
(x, t)
T
1, i
k,
α
k,
α
T
Interface
= [T
1
(x, t) + T
2
(x, t)]/2
(a) (b)
Figure IVa.9.2. Semi-infinite solids in perfect contact (a) (
ρ
ck)
1
≠ (
ρ
ck)
2
and (b) (
ρ
k)
1
=
(
ρ
ck)
2
Applying Equation IVa.9.10 and solving for the interface temperature, T
1, s
= T
2,
s
= T
s
, we find:
21
,22,11
)()(
)()(
ckck
TckTck
T
ii
s
ρρ
ρρ
+
+
=
IVa.9.13
Equation IVa.9.13 indicates that the surface temperature approaches the tempera-
ture of solid, which has higher
ρ
ck. If both solids are made of the same material,
then the interface temperature is T
s
= [T
1, i
+ T
2, i
]/2. This case is shown in Fig-
ure IVa.9.2(b).
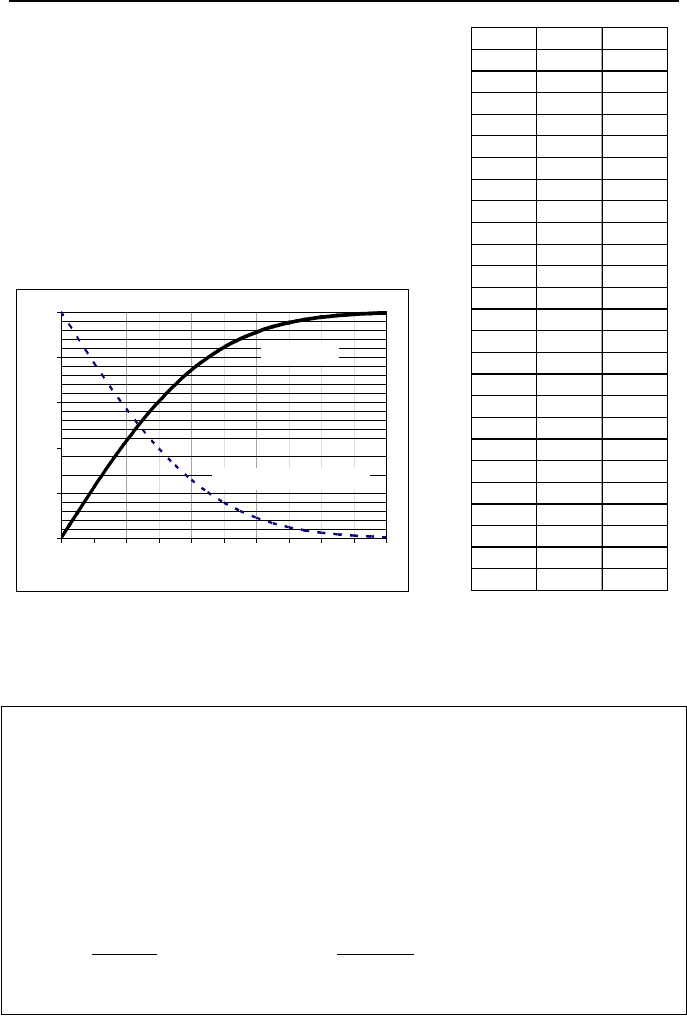
9. Analytical Solution of Transient Heat Conduction 491
0
0.2
0.4
0.6
0.8
1
00.20.40.60.811.21.41.61.82
Error Functio
n
Complementary Error Functio
n
Function
s
serferfc
001
0.05 0.05637 0.94363
0.1 0.11246 0.88754
0.15 0.168 0.832
0.2 0.2227 0.7773
0.25 0.27633 0.72367
0.3 0.32863 0.67137
0.35 0.37938 0.62062
0.4 0.42839 0.57161
0.5 0.5205 0.4795
0.6 0.60385 0.39615
0.7 0.6778 0.3222
0.8 0.7421 0.2579
0.9 0.79691 0.20309
1 0.8427 0.1573
1.1 0.8802 0.1198
1.2 0.91031 0.08969
1.3 0.93401 0.06599
1.4 0.95228 0.04772
1.5 0.9661 0.0339
1.6 0.97635 0.02365
1.7 0.98379 0.01621
1.8 0.98909 0.01091
1.9 0.99279 0.00721
2 0.99532 0.00468
Figure IVa.9.3. Gaussian error function and complementary error function
Example IVa.9.3. Two blocks, treated as semi-infinite solids, are brought into
perfect contact. The blocks are made of aluminum (
α
= 9.7E-5 m
2
/s) and are ini-
tially at 0 C and 150 C. Find temperature at a depth of 11 cm in each block 2 min-
utes into the perfect contact.
Solution: Since both blocks are made of the same material (k
A
= k
B
), the slopes of
the temperature profile are the same in the two blocks. Hence, T
s
= (0 + 150)/2 =
75 C.
arg = x/2(
α
t)
0.5
= 0.11/[2(9.7E-5 × 2 × 60)
0.5
] = 0.5, erf(arg
1
) = 0.52
S
1
(x, t) = =
−
−
750
75
1
T
0.52 and S
2
(x, t) = =
−
−
75150
75
2
T
0.52
We find T
1
= 36 C and T
2
= 114 C.
