Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

492 IVa. Heat Transfer: Conduction
9.3. Semi-infinite Bodies and Harmonically Oscillating Temperature
at the Boundary
An example of rapidly oscillating temperature is exposure of the cylinder wall of
an internal combustion engine to the combustible gas and the combustion prod-
ucts. Another example, but for low frequency oscillation, includes exposure of the
earth’s surface to the seasonal changes in the weather temperature. Let’s treat
earth as a semi-infinite solid and examine the latter case in more detail. Note that
for oscillating temperature at the boundary, we do not need an initial condition, as
the temperature penetration is also oscillatory, satisfying the steady state solution.
Equation IVa.2.3 still applies, however, we introduce dimensionless ratios to sim-
plify the equation. For a sinusoidal oscillation, we show the average surface tem-
perature with
T
, the amplitude of the oscillation with ∆T, and the angular fre-
quency with
ω
. The three dimensionless ratios are for temperature, time, and
location:
αωζωθ
2//and,, xt
T
TT
==Ω
∆
−
=
We first find T in terms of
θ
as
θ
TTT ∆+= . We then carry out the derivatives
for Equation IVa.2.3 using the chain rule for differentiation to obtain
∂T/∂x=
(dT/d
ζ
)(d
ζ
/dx) and ∂T/∂t= (∂
θ
/∂Ω)(dΩ/dt) resulting in:
2
2
2
2
2
ζ
θ
α
ω
∂
∂
∆=
∂
∂
T
x
T
and
Ω∂
∂
∆=
∂
∂
θ
ω
T
t
T
Substituting in Equation IVa.2.3, the governing equation for harmonically oscillat-
ing boundary temperature becomes:
ω
θ
ζ
θ
∂
∂
=
∂
∂
2
2
2
1
subject to t
ωθ
ζ
cos
0
=
=
and =
>0
ζ
θ
finite. As derived by Carslaw and de-
scribed by Lienhard, we try a solution in the form of
)cos(
ζθ
ζ
−Ω=
−
e , result-
ing in the following answer:
»
»
¼
º
«
«
¬
ª
−=
∆
−
−
xte
T
TT
x
α
ω
ω
αω
2
cos
2/
Example IVa.9.4. How deep should we dig the ground in high summer to find
the coldest part of the earth?
α
Earth
= 0.139E-6 m
2
/s.
Solution: The coldest part is due to the temperature penetration during the pre-
ceding winter. In this case, the angular frequency is
ω
= 2
π
rad/year. To find the
location of T
min
, we try a solution in the following form: )cos(
ζθ
ζ
−Ω=
−
e =

9. Analytical Solution of Transient Heat Conduction 493
ζ
ζ
cos
−
e . Initially, Ω =
ω
t = 0. To find
ζ
, we take the derivative of
θ
and set it
equal to zero:
()
[]
0sincos =+−=
ζ
ζζ
θ
e
dt
d
This results in
ζ
tan
= –1, corresponding to
ζ
= 3
π
/4, 7
π
/4, 11
π
/4, etc. For the
first answer, we find: 4/3)2/(
παω
=x . Substituting for
ω
= 2
π
N = 2 ×
π
/(365
× 24 × 3600) = 0.199E-6 s, we find
x = (3
π
/4)/[0.199E-6/(2 × 0.139E-6)]
1/2
= 2.783 m.
9.4. 1-D Transient Heat Conduction, Plate, Cylinder, and Sphere
Our goal here is to find analytical solutions to one-dimensional transient heat con-
duction in an infinite plate, infinite cylinder, and sphere. In all three cases, the ob-
ject is initially at the uniform temperature of T
i
and suddenly exposed to a convec-
tion boundary specified as T
f
and h. Similar to the steady state solution for a
rectangular plate, the technique of separation of variables can be used to find ana-
lytical solutions in series form for such objects. Heisler has shown that the center
temperature (T
o
) in these objects is obtained within 1% approximation by using
only the first term of the series solution:
¸
¸
¹
·
¨
¨
©
§
−=
−
−
2
2
exp
s
t
AC
TT
TT
BB
fi
fo
α
IVa.9.13
where coefficients C
B
and A
B
are only functions of the Biot number, Bi = hs/k and
are given in Table IVa.9.1. In Equation IVa.9.13, s = L for a slab, and s = R for a
thin solid cylinder and solid sphere. Equation IVa.9.13 applies only if the Fourier
number Fo =
α
t/s
2
> 0.2.
2R
r
r
x
h , T
f
h , T
f
T(x, t = 0) = T
i
T(r, t = 0) = T
i
2R
2L
Figure IVa.9.3. Plate (slab), infinite cylinder and sphere
Next, we examine plates, cylinders, and spheres. The approach is to first find
the center temperature of the object from Equation IVa.9.13 in conjunction with
Table IVa.1.9. Then use the center temperature to find the off center tempera-
tures.

494 IVa. Heat Transfer: Conduction
Case 1. Temperature Distribution in a Thin Plate. Having the center-plane
temperature from Equation IVa.9.13, temperature of any other point is found
from:
P(x, t) =
()
LxAAC
TT
TT
BBB
fi
f
/cos)Foexp(
2
−=
−
−
IVa.9.14
and the total heat transfer from:
B
B
A
A
txP
Q
Q
)sin(
),(1
0
−= IVa.9.15
where Q
o
= mc(T
i
– T
f
) where A
B
and C
B
are obtained from Table IVa.9.1.
Case 2. Temperature Distribution in an Infinite Solid Thin Cylinder. In the
case of a cylinder with diameter of 2R (s = R), having the centerline temperature
as a function of time, temperature of any point within the infinite cylinder can be
obtained from:
C(r, t) =
()
RrAJAC
TT
TT
BBB
fi
f
/)Foexp(
0
2
−=
−
−
IVa.9.16
and the total heat transfer from:
B
B
A
AJ
trC
Q
Q
)(
),(21
1
0
×−= IVa.9.17
where A
B
and C
B
are obtained from Table IVa.9.1.
Case 3. Temperature Distribution in a Sphere. In a solid sphere of diameter
2R (s = R), temperature at any point is obtained from the center temperature as:
()
RrA
rA
R
TT
TT
trK
B
Bfi
f
/sin),( =
−
−
=
and total heat transfer by:
3
0
cossin
),(31
B
BBB
A
AAA
trK
Q
Q
−
−=
where A
B
and C
B
are obtained from Table IVa.9.1. Note that the arguments of the
trigonometric functions are in radians. Methods of the analysis of transient heat
conduction in plates, cylinders and spheres are shown in the following examples.

9. Analytical Solution of Transient Heat Conduction 495
Example IVa.9.5. A brick wall, 30 cm thick and 80 C is suddenly exposed to an
environment of 10 C and 120 W/m
2
C. Find temperature at 5 cm from the center
plane 10 h after exposure.
Brick properties; k = 0.69 W/m·C, c = 840 kJ/kg·C, and
ρ
= 1602 kg/m
3
(
α
=
5.127E–7 m
2
/s).
Solution: We first find the Biot and the Fourier numbers:
Bi = hs/k = 120 × (0.30/2)/0.69 = 26 and Fo = 5.127E–4 × 36000/(0.15)
2
= 0.82
From Table IVa.9.1 we find A
B
= 1.5106 and C
B
= 1.2709. From Equation
IVa.9.14:
P(x, t) = C
B
exp(–
2
B
A Fo)cos(A
B
x/L) = [1.2709exp(–1.5106
2
× 0.82)]cos(1.5106 ×
5/15)= 0.171
T = T
f
+ (T
i
– T
f
) × P(x, t) = 10 + (80 – 10) × 0.171 = 22 C.
In the next example, we examine transient analysis in infinite solid cylinders.
Example IVa.9.6. A long steel cylinder with a diameter of 8 cm and an initial
temperature of 250 C is suddenly exposed to a convection boundary of 25 C and
500 W/m
2
·C. Find the temperature at r = 0 cm and at r = 2 cm at 2 minutes after
the exposure. (k = 35 W/m·C,
ρ
= 7800 kg/m
3
, and c = 0.48 kJ/kg·C).
Solution: We need the Biot and the Fourier numbers:
Bi = hR/k = 500 × (4/100)/35 = 0.571 and
α
= k/
ρ
c = 35/(7800 × 480) = 9.35E-6 m/s
2
Fo = 9.35E-6 × 120/0.04
2
= 0.7
To find the centerline temperature from Equation IVa.9.13, we find coefficients A
B
and C
B
from Table IVa.9.1 as A
B
= 0.996 and C
B
= 1.1286. Hence,
C
o
(r, t) = C
B
exp( Fo
2
B
A− ) = 1.1286exp(–0.996
2
× 0.7) = 0.563
Therefore, the center temperature is:
T
o
= T
f
+ (T
i
– T
f
)C
o
(r, t) = 25 + 0.563(250 – 25) = 152 C
From Equation IVa.9.16 we find:
C(r, t) =
()
RrAJtrC
Bo
/),(
0
= 0.563 × J
o
(0.996 × 2/4) = 0.528
Therefore, temperature at r = 2 is found as:
T(r = 2) = T
f
+ (T
i
– T
f
)C(r, t) = 25 + (250 – 25)× 0.528 = 143.9 C
Total heat transfer per meter of this cylinder in this period is q
′
= 2135 kJ/m.
The next example deals with transient heat conduction in spheres.

496 IVa. Heat Transfer: Conduction
Example IVa.9.7. A sphere with D = 12 cm and T
i
= 300 C is suddenly exposed
to a convection boundary of 25 C and 100 W/m
2
·C. Find temperature at a radius
of r = 0 and r = 2 cm, 85 s after the exposure.
(k = 52 W/m·C,
ρ
= 7270 kg/m
3
, c = 420 J/kg·K).
Solution: We find
α
as:
α
= 52/(7270 × 420) = 1.7E-5 m
2
/s.
For Bi = 100 × 0.06/52 = 0.115, from Table IVa.9.1 we also find A
B
= 0.576 and
C
B
= 1.034
arg = Fo
2
B
A− =
22
/ stA
B
α
− = –(0.576)
2
(1.7E-5)(85)/(0.06)
2
= –0.133
T
o
= T
f
+ (T
i
– T
f
)exp(arg) = 25 + 1.034(300 – 25)exp(–0.133) = 273.97 C
T(r = 2) = T
f
+ (T
o
– T
f
)(R/A
B
r)sin(A
B
r/R) = 25 + (273.97 – 25)(6/2 × 0.576)sin(2 ×
0.576/6)
T(r = 2) = 25 + (273.97 – 25)(5.208)sin(0.192) = 272.4 C
Is the lumped capacitance method appropriate here? Find the sphere temperature
by using Equation IVa.4.2 (note, Bi << 1).
9.5. Multi-dimensional Transient Heat Conduction
Analytical solution to the steady state heat conduction in a rectangular plate and to
the transient heat conduction in infinite plates, infinite cylinders, and spheres is
obtained by the method of the separation of variables. In this method, temperature
distribution is in the form of the product of various functions. An example of such
analytical solution is discussed in Chapter VIIb where temperature distribution is
sought in a rectangular plate subject to one non-homogenous and three homoge-
nous boundary conditions. Equation VIIb.2.27 gives the series solution obtained
for this case.
2L
y
2L
z
2L
x
Infinite
Plate
Rectangular
Parallelpiped
Infinite
Cylinder
Infinite
Plate
2R
2L
x
r
Finite
Cylinder
Figure IVa.9.4. Obtaining multidimensional objects from one-dimensional solids
Similar approach can be used to find transient temperature distribution in other
objects if they can be reduced to such basic configurations for which analytical so-
lutions already exist. For example, we can use two infinite plates to construct an

9. Analytical Solution of Transient Heat Conduction 497
infinite parallelepiped. To find temperature distribution in an infinite parallelepi-
ped, we can then multiply the solutions of the two infinite plates. Similarly, we
can obtain a finite cylinder from the intersection of an infinite cylinder and an in-
finite plate. Temperature distribution in the finite cylinder is the product of the so-
lutions of the infinite plate and the infinite cylinder. These are shown in Fig-
ure IVa.9.4 and Table IVa.9.2.
Table IVa.9.1. Heisler coefficients for center temperature
Thin Plate Infinite Cylinder Sphere
Biot
Number
A
B
C
B
A
B
C
B
A
B
C
B
0.01 0.0998 1.0017 0.1412 1.0025 0.1730 1.0030
0.02 0.1410 1.0033 0.1995 1.005 0.2445 1.0060
0.04 0.1987 1.0066 0.2814 1.0099 0.3450 1.0120
0.06 0.2425 1.0098 0.3438 1.0148 0.4217 1.0179
0.08 0.2791 1.0130 0.3960 1.0197 0.4860 1.0239
0.1 0.3111 1.0161 0.4417 1.0246 0.5423 1.0298
0.2 0.4328 1.0311 0.6170 1.0483 0.7593 1.0592
0.3 0.5218 1.0451 0.7465 1.0712 0.9208 1.0880
0.4 0.5932 1.058 0.8516 1.0931 1.0528 1.1164
0.5 0.6533 1.0701 0.9408 1.1143 1.1656 1.1441
0.6 0.7051 1.0814 1.0185 1.1345 1.2644 1.1713
0.7 0.7506 1.0919 1.0873 1.1539 1.3525 1.1978
0.8 0.7910 1.1016 1.1490 1.1724 1.4320 1.2236
0.9 0.8274 1.1107 1.2048 1.1902 1.5044 1.2488
1 0.8603 1.1191 1.2558 1.2071 1.5708 1.2732
2 1.0769 1.1785 1.5995 1.3384 2.0288 1.4793
3 1.1925 1.2102 1.7887 1.4191 2.2889 1.6227
4 1.2646 1.2287 1.9081 1.4698 2.4556 1.7202
5 1.3138 1.2403 1.9898 1.5029 2.5704 1.787
6 1.3496 1.2479 2.0490 1.5253 2.6537 1.8338
7 1.3766 1.2532 2.0937 1.5411 2.7165 1.8674
8 1.3978 1.257 2.1286 1.5526 2.7654 1.8920
9 1.4149 1.2598 2.1566 1.5611 2.8044 1.9106
10 1.4289 1.262 2.1795 1.5677 2.8363 1.9249
20 1.4961 1.2699 2.2881 1.5919 2.9857 1.9781
30 1.5202 1.2717 2.3261 1.5973 3.0372 1.9898
40 1.5325 1.2723 2.3455 1.5993 3.0632 1.9942
50 1.5400 1.2727 2.3572 1.6002 3.0788 1.9962
100 1.5552 1.2731 2.3809 1.6015 3.1102 1.9990

498 IVa. Heat Transfer: Conduction
Table IVa.9.2. Solution for multidimensional solids
Solid Geometry Semi-
infinite
Solid
Infinite Plate Infinite
Cylinder
Semi-infinite Plate S(x, t) P(x, t) –
Infinite Rectangular Bar -
P
1
(x, t) × P
2
(x, t)
–
Semi-infinite Rectangular Bar S(x, t)
P
1
(x, t) × P
2
(x, t)
–
Rectangular Parallelepiped -
P
1
(x, t) × P
2
(x, t) × P
3
(x, t)
–
Semi-infinite Cylinder S(x, t) C(r, t)
Short Cylinder - P(x, t) C(r, t)
Example IVa.9.8. A stainless steel cylinder with a diameter of 2 in, length of 3
in, and initial temperature of 650 F is suddenly exposed to a convection boundary
of 65 F and 50 Btu/ft
2
·h·F. Find the temperature at a radius of r = 0.5 in and
height of 1 in from the mid-plane, 2 minutes after the exposure.
Solution: From Table IVa.9.2, we note that temperature distribution in a short
cylinder is given by: T(r, x, t) = P(x, t)C(r, t). We then find Bi number for the
plate and for the cylinder:
Bi Fo A
B
C
B
P(x, t) C(r, t)
Plate 0.716 0.323 0.757 1.093 0.796 –
Cylinder 0.478 0.724 0.921 1.110 – 0.569
Hence, for the short cylinder:
Θ
(r, t) = [T(r, t) – T
f
]/[T
i
– T
f
] = P(x, t) × C(r, t) = 0.796 × 0.569 = 0.453
T(r, t) = 65 + (650 –65) × 0.453 = 330 F. Also, Q = 340.22 × (3/12) = 85 Btu.
Example IVa.9.9. An aluminum cylinder is exposed to a convection boundary.
Find temperature at the specified location and time.
Data: k = 124 Btu/ft·h·F, c = 0.2 Btu/lbm·F,
ρ
= 170 lbm/ft
3
, T
i
= 400 F, T
f
= 50 F,
h = 100 Btu/ft
2
·h·F, 2R = 2 in, 2L = 5 in, r = 0.5 in, x = 1.5 in, t = 30 s.
Solution: Bi(plate) = hL/k = 100(5/12)/124 = 0.168 and Bi(cylinder) = hR/k =
100(1/12)/124 = 0.067. We then use Table IVa.5.1 and Equations IVa.5.14 and
IVa.5.16.
Bi Fo A
B
C
B
P(x, t) C(r, t)
Plate 0.168 0.700 0.394 1.026 0.903 –
Cylinder 0.067 4.376 0.363 1.017 – 0.567
Hence, for the short cylinder:
Θ
(r, t) = [T(r, t) – T
f
]/[T
i
– T
f
] = P(x, t) × C(r, t) = 0.903 × 0.567 = 0.512
10. Numerical Solution of Heat Conduction Equation 499
T(r, t) = 50 + (400 – 50) × 0.512 = 229 F.
Problems involving temperature distribution in solids can be easily solved by
using the software on the accompanying CD-ROM.
10. Numerical Solution of Heat Conduction Equation
As much as we try to find analytical solutions for engineering problems, there are
many cases for which analytical solutions cannot be found. In heat conduction,
this occurs when we are dealing with complex geometries, when properties are
strongly dependent on temperature, when internal heat generation rate is a func-
tion of space and time, when boundary conditions are non-linear, or in some cases
due to all these factors combined. Therefore, it becomes indispensable to resort to
modeling the problem numerically and solving the set of equations by computer.
Since numerical techniques are described in Chapter VIIe, we only apply the re-
sults in this chapter. In the following example, a plate with a specified internal
heat generation and unit depth is subjected to three types of boundary conditions,
temperature, convection, and insulated boundaries.
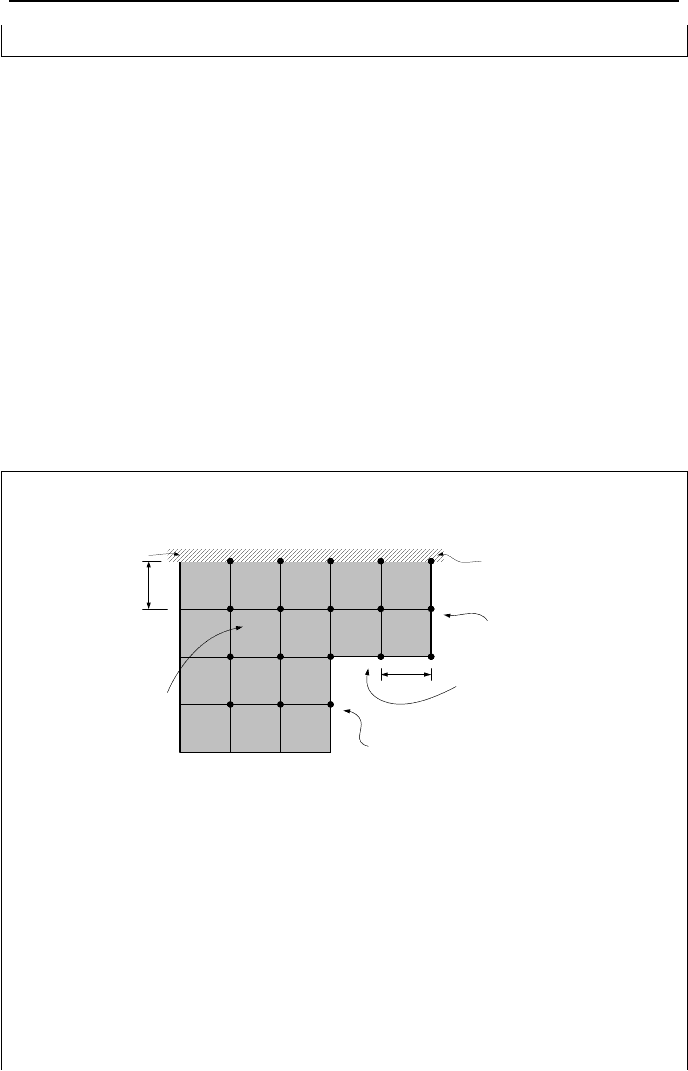
Example IVa.10.1. Use the information given in the figure to find temperature
distribution in the plate.
0.1m
0.1m
h = 75 W/m
2
K
T
f
= 50 C
T = 100 C
T = 200 C
Insulated Boundary
1514
10 1311
12
876
2
54
3
1
16 17
9
18
q''' = 20 kW/m
3
.
k=10 W/m K
h = 100 W/m
2
K
T
f
= 50 C
h = 100 W/m
2
K
T
f
= 50 C
Insulated Boundary
.
.
.
.
Solution: Nodes 1, 2, 4, 5, 9, 10, 11, and 12 are interior nodes to which Equa-
tion VIIe.3.5 applies. Nodes 3, 7, and 13 are plane surface nodes subject to
convection boundary. Nodes 6 and 8 are corner nodes. Nodes 14 through 17 are
plane surface nodes subject to insulated boundary condition. Node 18 is on an in-
sulated boundary and also faces a convection boundary. For internal nodes we
have:
Node 1: T
2
+ T
4
– 4T
1
+ 20 = – 300
Node 2: T
1
+ T
3
+ T
5
– 4T
2
+ 20 = – 100
Node 4: T
1
+ T
5
+ T
9
– 4T
4
+20 = – 200
Node 5: T
2
+ T
4
+ T
6
+ T
10
– 4T
5
+ 20 = 0
Node 9: T
4
+ T
10
+ T
14
– 4T
9
+ 20 = – 200
Node 10: T
5
+ T
9
+ T
11
+ T
15
– 4T
10
+ 20 = 0

500 IVa. Heat Transfer: Conduction
Node 11: T
6
+ T
10
+ T
12
+ T
16
– 4T
11
+ 20 =0
Node 12: T
7
+ T
11
+ T
13
+ T
17
– 4T
12
+ 20 = 0
For plane surface nodes with convection boundary we have different heat transfer
coefficient for vertical and for horizontal planes. For nodes on a vertical plane,
the Biot number is Bi / 1hxk=∆ = whereas for nodes on a horizontal plane the
Biot number is Bi = 75.0/ =∆ kxh :
Node 3: 2T
2
+ T
6
+100 – 2 (2 + 1) T
3
+ 20 = – 100
Node 7: T
6
+ T
8
+ 2T
12
– 2(2 + 0.75) T
7
+ 20 = – 1.5T
f
Node 13: 2T
12
+ T
8
+ T
18
– 2(2 + 1) T
13
+ 20= –100
For the internal corner node subject to convection boundaries we have:
Node 6: 2(T
5
+ T
11
) + (T
3
+ T
7
) – (6 + 1.75) T
6
+ 30 = – 1.75T
f
For the corner node subject to convection boundaries we have:
Node 8: (T
7
+ T
13
) – (2 + 1.75) T
8
+ 10 = – 1.75 T
f
For plane surface nodes subject to the insulated boundary we have:
Node 14: 200 + T
15
+ 2T
9
– 4T
14
+ 20 = 0
Node 15: T
14
+ T
16
+ 2T
10
– 4T
15
+ 20 = 0
Node 16: T
15
+ T
17
+ 2T
11
– 4T
16
+ 20 = 0
Node 17: T
16
+ T
18
+ 2T
12
– 4T
17
+ 20 = 0
Finally, for the corner node subject to insulation and convection boundaries we
have:
Node 18: (T
13
+ T
17
) – (2 + 1) T
18
+ 10 = – T
f
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
©
§
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
¨
©
§
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
60
20
20
20
220
120
20
20
20
220
5.97
95
5.117
20
220
220
120
320
310001000
000000000
141000200000000000
014100020000000000
001410002000000000
000141000200000000
100016100020000000
01
0001410001000000
001000141000100000
000100014100010000
000010001400001000
000001000075.31000000
00000020001
5.5100000
000000020000175.720100
000000001000141010
000000000100014001
000000000000100620
000000000000010141
000000000000001014
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
T
The results are shown in the figure.

10. Numerical Solution of Heat Conduction Equation 501
0.1m
0.1m
h = 75 W/m
2
K
T
f
= 50 C
T = 100 C
T = 200 C
Insulated
Boundary
1514
10
13
11
12
876
2
54
31
16
17
9
18
q''' = 20 kW/m
3
.
k=10 W/m K
h = 100 W/m
2
K
T
f
= 50 C
h = 100 W/m
2
K
T
f
= 50 C
159 135 101
183 158 119 96 75
194 175 147 119 87.4
197 180 155 126 91.2
Insulated
Boundary
.
.
.
In this example, we assumed a uniform heat generation rate. However, if the
rate of heat generation is a function of location, we could easily account for spatial
dependence of the internal heat generation. To obtain more accurate values for
temperatures, we should use smaller mesh sizes. The above example dealt with
rectangular coordinates. We can use the same procedure and solve problems in
orthogonal but not rectangular, such as cylindrical and spherical coordinates.
QUESTIONS
−
Are homogeneous substances are necessarily isotropic?
− Does conduction heat transfer apply only to solids?
− Does convection heat transfer apply only to fluids?
− What is the difference between heat flux and the linear heat generation rate?
− Consider a solid sphere of diameter D in which heat is produced in the center of
the sphere and is steadily removed at the surface. Is heat flux at r = D/6 equal
to the heat flux at r = D/3?
− Consider a solid sphere of diameter D in which heat is produced in the center of
the sphere and is steadily removed at the surface. Is the rate of heat transfer at r
= D/6 equal to the rate of heat transfer at r = D/3?
− What is the difference between a gas thermal conductivity at the viscous state
versus the molecular state?
− Regarding thermal conduction, what type of a substance is wood?
− What is the thermal capacitance of silver at 300 F?
− Define thermal diffusivity. Consider solids A and B being at the same tempera-
ture. However, solid A hasa higher thermal diffusivity than solid B. Which is
more effective in transferring than in storing energy?
− Is aluminum more effective in storing energy than zinc at the same tempera-
ture?
− Define thermal resistance. One side of a plate is warmer than the other side. Is
thermal resistance in this plate inversely related to the thickness of the plate?
− What is radiation heating? If a plate is bombarded by
γ
-radiation why is there a
maximum temperature in the plate? How do you find the location and the mag-
nitude of the maximum temperature?
