Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

512 IVa. Heat Transfer: Conduction

number of the plates to dissipate 10.55 W at steady state operation. Data: T

base

85 F, T

= 65 F, h = 1 Btu/h·ft

·F, L = 10 in, b = 1 in,

= 0.03 in. [Ans.: 15].

55. A longitudinal fin of triangular profile is made of aluminum. The base tem-

perature is 350 C. The top and the bottom of the fin are exposed to a convection

boundary given as T

= 30 C and h = 50 W/m

·K. Find a) the fin temperature at x =

l/2 and b) the heat removed by the fin. Additional data: b = 1 cm and l = 1.5 cm.

56. An annular fin is used to cool an internal combustion engine. Find a) the total

rate of heat transfer from the fin b) fin temperature at r = r

/2, c) fin effectiveness,

defined as the rate of heat loss from the fin to the rate of heat loss without the fin,

and d) fin efficiency, defined as the rate of heat loss from the fin to the rate of heat

loss from the fin if the entire fin were at the base temperature. The fin is made of

commercial bronze. Data: r

= 20 cm, r

= 10 cm, fin thickness = 5 mm, base

temperature = 250 C, T

= 15A C, and h = 100 W/m·K.

[Ans.: T(15 cm) = a) 136 C, b) 611 W, c) about 8.3, and d) about 52%].

57. A longitudinal fin of rectangular profile is used to enhance heat removal from

a wall maintained at 450 F. The fin is made of carbon steel. The fin is exposed to

a convection boundary. Find a) temperatures at the tip of the fin and b) the rate of

heat loss from the fin, c) fin effectiveness, defined as the rate of heat loss from the

fin to the rate of heat loss without the fin, and d) fin efficiency, defined as the rate

of heat loss from the fin to the rate of heat loss from the fin if the entire fin were at

the base temperature. Fin length = 1 in, fin thickness = 1/8 in, fin width = 6 in,

= 72 F, h = 5 Btu/h·ft

·F. [Ans.: b) 159 Btu/h].

58. We plan to design an engine with an outside diameter of 10 cm and height of

12 cm. The outside surface is at 200 C. Several means of cooling the engine are

to be evaluated including the use of cylindrical spines. The spines to be evaluated

have a diameter of 1 in and a length of 3 cm. Find a) the amount of heat removed

by a total of 240 equally spaced spines and b) find the fin efficiency. Assume the

surface temperature is uniform over the entire surface of the engine. Data: k = 50

W/m·K, T

= 200 C, T

= 12 C, and h = 13 W/m

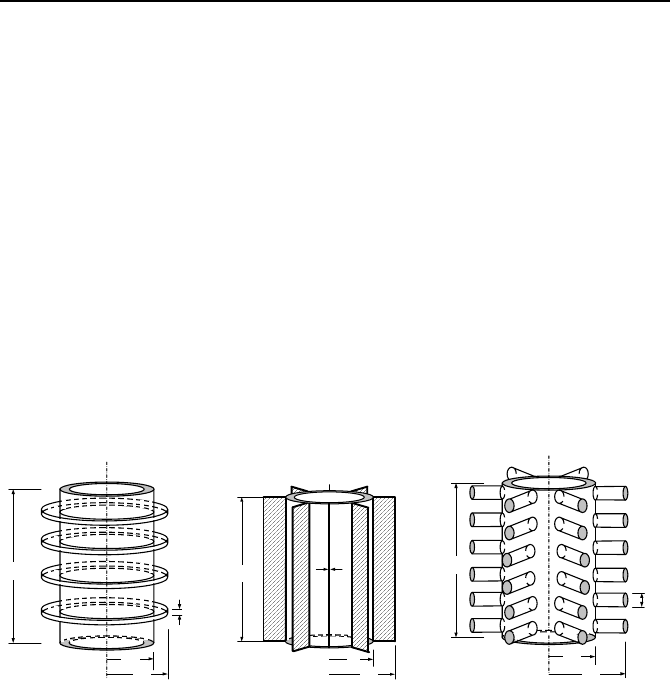
·K. [Ans.: a) 0.6 kW].

59. A pressure vessel containing a mixture of water and steam is shown in the

figure. The flange attached to the vessel head is secured tightly to the lower

flange attached to the rest of the vessel by 24 bolts. If the base temperature in the

bolt at the connection to the upper nut is 350 F, find the amount of heat lost by the

last 3 in of the stainless steel bolts. Use T

= 70 F, h

= 1 Btu/h·ft

·F, and k

Bolt

= 10

Btu/h·ft·F. [Ans. 0.125 kW].

10"

D = 1 m

Fin

= 1.2 m

Figure for Problem 54 Figure for Problem 59 Figure for Problem 60

Questions and Problems 513

60. A pipe carrying superheated steam is equipped with an expansion joint to pre-

vent structural damage in the case of temperature driven transients. The expan-

sion joints are thin stainless steel plates welded at the tip to other plates and at the

base to the steel pipe. Find the amount of heat loss to the surroundings in the case

where the plates are not insulated. There are 3 sets of expansion joints as shown

in the figure. In the pipe, steam is flowing at 150 C while the surrounding is at

20 C. Additional data: h

= 250 W/m·K, h

= 15 W/m·K.

61. Due to the manufacturing preferences, only three types of fins are to be con-

sidered for the cooling of an air-cooled internal combustion engine.. These are

annular fins with rectangular profile, straight fins of uniform cross section, and pin

fins (cylindrical spines). The cylinder height is 20 cm and has a base diameter

(2r

) of 8 cm. All fins have insulated tips. The cylinder base temperature is 200

C, the cooling air temperature is 30 C, and the heat transfer coefficient is esti-

mated at about 50 W/m

·K. Fins are spaced equally and uniformly. Subscripts A,

S, and P are used to represent annular fin, straight fin, and pin fin, respectively.

Use the following data to find: a) the rate of heat removal from each type of fin

and b) temperature at the tip (r = r

) of each fin.

Data: L = 20 cm, r

= 4 cm, r

= 9.55 cm,

= 8 mm,

= 3 mm, d

= 2 cm,

= 4, N

= 6, N

= 36.

62. Two cylindrical aluminum spines, having equal length and equal outside di-

ameter are attached to a hot wall. One of the spines is made of a solid rod and the

other is a pipe. Compare the rate of heat loss from these otherwise identical fins.

The outside diameter is 5 cm and the pipe inside diameter is 4 cm. The wall is at

300 C and the ambient temperature and heat transfer coefficient are 35 C and

15 W/m

·K, respectively. Assume the same heat transfer coefficient for the inside

of the pipe.

Section 9

63. Consider two blocks of nickel, treated as semi-infinite solids. Initially, one

block is at 0 C and the other at 100 C. We now bring these blocks in contact. Ig-

nore the contact thermal resistance and find the temperature of a point located

5 cm from the common boundary in either block, 5 minutes after the contact. Use

Nickel

= 2.3E-5 m

/s. [Ans.: 34 C and 66 C].

514 IVa. Heat Transfer: Conduction

64. Consider two blocks treated as semi-infinite solids. One block is made of

copper and the other of stainless steel. Initially, the block made of copper is at 0 C

and the block made of stainless steel at 100 C. We now bring these blocks in con-

tact. Ignore the contact thermal resistance and find the temperature of a point lo-

cated 5 cm from the common boundary in either block, 5 minutes after the contact.

65. A PWR pressurizer is at 2200 psia. A sudden outsurge results in all the water

leaving the pressurizer. Find the temperature at a depth of 1 in, 10 minutes into

the event. Steel properties; k = 25 Btu/ft·h·F and

= 1.3E-4 ft

/s. h = 75

Btu/ft·h·F. Initial water volume 850 ft

. Pressurizer volume 1700 ft

. [Hint: T

sat

(2200 psia) = 649.5 F and T

= T

sat

) where P

= P

)/VV(

]. (Ans. P

875 psia, T

= 528.6 F, arg

= 0.15, arg

= 0.952, arg

= 0.988, and T = 545 F)

66. A long steel rod is suddenly exposed to a convection boundary. Find the tem-

perature at r = 0.35 in after a duration of 75 s . Data: rod diameter = 2 in, k = 20

Btu/ft·h·F, c = 0.1 Btu/lbm·F,

= 488 lbm/ft

, T

= 550 F, T

= 75 F, h =

100 Btu/ft

·h·F. [Ans.: T

= 282 F, T(r = 0.35 in) = 277 F, Q = 305 Btu/ft].

67. A long slender steel bar initially at 400 C is exposed to a convection boundary

of T

= 35 C and h = 375 W/m

·C. The bar diameter is 5 cm. Find the temperature

at r = 0.75 cm after 85 seconds of exposure.

[Ans.: T

= 241.5 C, T

= 239 C].

68. Aluminum balls are heated up to 580 K and then exposed to air at 283 K to

cool down with an average heat transfer coefficient of 25 W/m

·K. The balls are 3

cm in diameter. Find the temperature at r = 0.5 cm after 75 seconds of exposure.

Is the lumped capacitance an acceptable solution here? [Ans.: 329 K].

69. A sphere made of fire-clay brick is heated to 500 C and cooled in ambient air

at T

= 35 C and h = 250 W/m·C. The sphere has a diameter of 10 cm. Find the

temperature at a radius of 2.5 cm after 30 minutes. Data: k = 1 W/m·C, c =

1 kJ/kg,

= 2000 kg/m

. [Ans.: K(r, t) = 0.663. T = 343 C].

70. A short stainless steel cylinder (D = 8 cm and 2L = 6 cm) is initially at 327 C.

Find the temperature at a location identified as r = D/2 and x = 0 after being sud-

denly exposed for 3 minutes to air at T

= 27 C and a heat transfer coefficient of

h = 500 W/m·C. [Ans.: P(x, t) = 0.635 and C(r, t) = 0.337. T = 91 C].

71. A long stainless steel rod (

= 7900 kg/m

, c = 0.526 kJ/kg·K, and k = 17.4

W/m·K) having a diameter of 5 cm, is initially at 200 C when its surface is ex-

posed to an ambient at 300 K with a heat transfer coefficient of 600 W/m

·K. Af-

ter 2 min exposure, find: a) the centerline temperature and b) the temperature at a

distance of 1 cm from the rod centerline. c) Find the temperature of 10 equally-

spaced points inside the rod after 2 min of exposure and plot the results. d) Track

the centerline temperature every 5 seconds and plot the results for the 2 minutes of

exposure. [Ans.: a) 93 C and b) 90 C].

Questions and Problems 515

72. A solid rectangular parallelepiped is made of aluminum and is initially at

20 C. The base is a 2 cm by 3 cm rectangle and the height of the parallelepiped is

5 cm. The parallelepiped is now dropped into hot oil at 150 C. Find: a) the tem-

perature of point P and b) the temperature of the center of the parallelepiped after

2 min of exposure to hot oil. Point P is located 1 cm above the center plane and

1 cm from each side.

73. A short cylinder having an initial temperature of 40 C is suddenly exposed to

a convection boundary of 300 W/m

·K. Use the data given below to find the tem-

peratures of points A, B, C, and D. Data: k = 26 W/m·K, c

= 0.349 kJ/kg·K,

8,666 lbm/m

. [Ans.: T

= 176 C, T

= 184 C, T

= 186.5 C, T

= 180 C].

CCD

Section 10

74. A cylindrical spine is used is shown in the figure. a) Use the given data to

find the temperature distribution in the solid rod. The tip of the fin loses heat by

convection. b) Find the temperature of a node by numerical methods as described

in Section 3 of Chapter VII. First divide the fin into 5 equally spaced nodes. Re-

peat the solution for the number of nodes increased to 10 and finally to 20.

c) Compare the results obtained in part b with the analytical solution of part a.

Data: L = 20 cm, D = 2 cm, k = 50 W/m·C, T

= 250 C, T

= 35 C, h = 10 W/m

·C.

75. Two surfaces of a long L-shape object are maintained at temperatures T

(along the x-axis) and T

(along the y-axis) as shown in the figure. All other sur-

faces are exposed to a convection boundary (T

and h). Use the method described

in Section 3 of Chapter VII to find temperatures at location 1, 5, and 7. Data: a =

2 cm, Ts

= 50 C, T

= 100 C, T

= 15 C, h = 10 W/m

·C.

76. All surfaces of an infinitely long heating element, having a cross section in

the shape of a cross, are maintained at 300 C. Due to symmetry, only a quarter of

the cross section is shown in the figure. Heat is uniformly produced in the ele-

ment at a rate of 100 kW/m

. Find the temperature distribution in the element at

the locations shown in the figure. The element thermal conductivity is 35 W/m·K.

All surfaces are exposed to a convection boundary condition of T

= 40 C and h =

1200 W/m

·C.

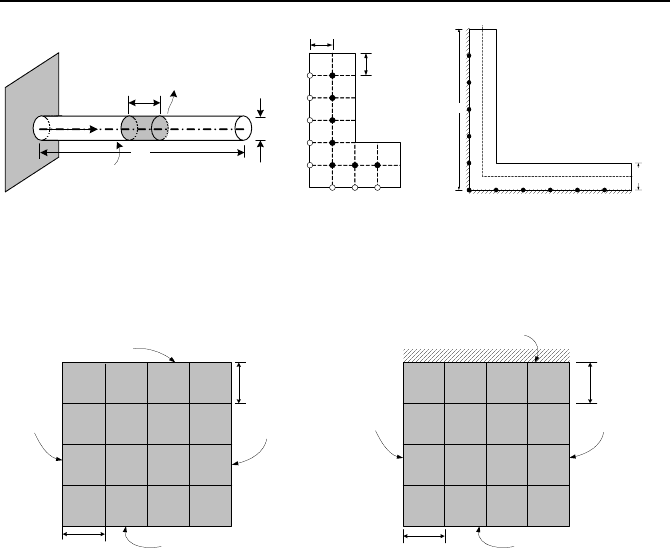
516 IVa. Heat Transfer: Conduction

∆x

6 cm

1 cm

Figure for Problem 74 Figure for Problem 75 Figure for Problem 76

77. The surfaces of a long solid square bar are maintained at the temperatures

shown in the figure. The solid thermal conductivity is 25 W/m·C. Find the tem-

peratures of the nodes shown in the figure.

= 200 C

1 cm

= 20 C

= 200 C

1 cm

= 20 C

Insulated Boundary

Figure for Problem 77 Figure for Problem 78

78. One side of the bar of Problem 76 is now insulated. Find the temperature dis-

tribution in the bar.

79. Use the given data to find the temperature distribution in the plate with one

side insulated, three sides are isothermal and the indentation is exposed to a con-

vection boundary.

80. A plate-type fuel element, having a thermal conductivity of 2 W/m·K, pro-

duces heat. The heat source is uniformly distributed, having a source strength of

2.4E8 W/m

. One side of the fuel is insulated (due to symmetry), one side is

maintained at 200 F, and remaining sides are exposed a convection boundary of

300 C and 34 kW/m

·K. Find the two-dimensional temperature distribution in the

fuel at steady state condition.

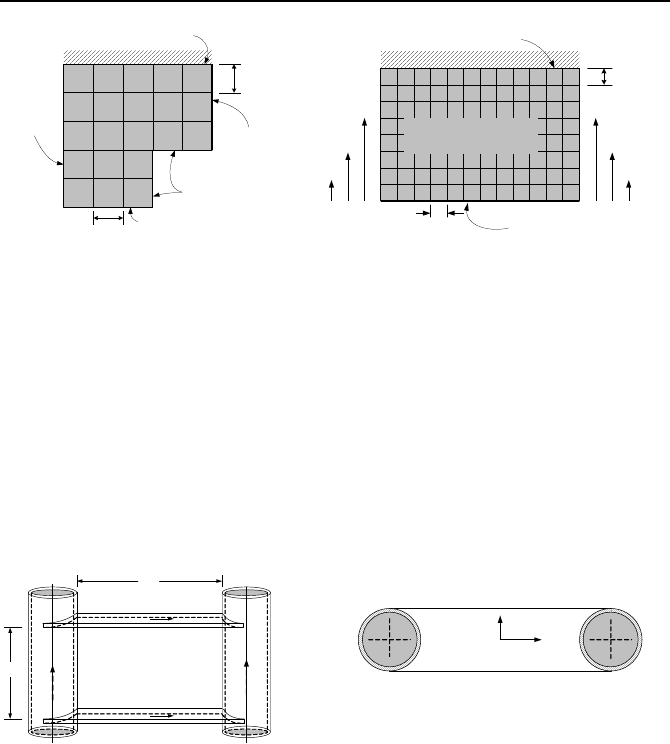
Questions and Problems 517

1 cm

= 20 C

Insulated Boundary

= 200 C

h = 1500 W/m K

= 20 C

h = 34 kW/m

= 300 C

h = 34 kW/m

= 300 C

Insulated boundary

= 200 C

1 mm

W/m8E0.1=

′′′



Figure for Problem 79 Figure for Problem 80

81. Shown in the figures are the elevation and the plan views of two pipes carry-

ing hot air. The air flow rate is 200 kg/s in each of the two 12 inch, schedule 40

steel pipes. The pipes are connected to each other by 2 steel support plates. The

plates have a thickness of 2 cm and are placed 50 cm apart from each other. The

distance between the pipes is 55 cm. Find a) temperature at x = 0 for steady state

operation in the bottom plate and b) find the temperature of the top plate at the

same location. Data: Assume a constant heat transfer coefficient of 2500 W/m

·K

inside the pipe. The air pressure and bulk temperature at the entrance to the pipe

(where the bottom plate is located) are 3 MPa and 300 C, respectively. The ambi-

ent temperature is 37 C and the heat transfer coefficient with the ambient is

12 W/m

·K. Assume that the pipes are smooth.

518 IVb. Heat Transfer: Forced Convection

IVb. Forced Convection

In Chapter IVa we often used the convection boundary condition to determine

temperature distribution in such cases as fuel rods, fins, and multi-dimensional

solids. However in all such cases, the heat transfer coefficient, h was specified.

Our primarily goal in this chapter is to find the heat transfer coefficient for a given

set of conditions. As we shall see, the magnitude of the heat transfer coefficient

depends on such factors as the type of fluid, the flow velocity, and the type of ap-

plication. The type of fluid in turn defines such fluid properties as viscosity, den-

sity, thermal conductivity, and specific heat. Flow velocity is a key parameter,

which is used in conjunction with temperature to determine the flow regime, being

laminar or turbulent. Finally, the type of application determines whether flow is

external such as flow over flat plates, cylinders, and spheres or internal such as

flow inside conduits. The immediate application of the heat transfer coefficient is

in finding the temperature distribution and the rate of heat transfer to or from a

substance. In this chapter we exclusively deal with forced convection heat trans-

fer. The characteristic of this heat transfer mode is the fact that the flow of fluid is

due to the operation of a pump, a compressor, or the rapid movement of an object

in the flow filed.

1. Definition of Forced Convection Terms

Newton’s law of cooling is the result of applying the Isaac Newton’s sugges-

tion in 1701 that if a body is placed in a medium at a lower temperature, then the

rate of change of temperature of the body is proportional to T

body

– T

where T

this relation is the temperature of the colder medium. Since the rate of change of

temperature of the body is also proportional to the rate of heat transfer from the

body, we may then conclude:

)(

fbody

TThq −=

′′



where h, the proportionality factor is known as heat transfer coefficient. To be

consistent, we replace T

body

with T

where subscript s represents a surface such as a

flat plat or the wall of a conduit.

Thermal boundary layer over a flat plate develops whenever there is a tem-

perature difference between a surface and the fluid flowing over the surface. The

hydrodynamic boundary layer and the associated velocity profile for flow of a vis-

cous fluid over a flat plate are shown in the left side of Figure IVb.1.1. Develop-

ment of a similar boundary layer, for a case where the flat plate is hotter than the

fluid, is shown in the right side of Figure IVb.1.1. The viscous forces are domi-

nant in the hydrodynamic boundary layer resulting in a velocity profile as shown

in the figure. Similarly, a temperature gradient exists in the thermal boundary

layer. At the edge of the boundary, both velocity and temperature inside the

boundary layer reach 99% of the free stream velocity (V

) and temperature (T

), re-

spectively. Also at the edge of the boundary layer where y = δ, we find that

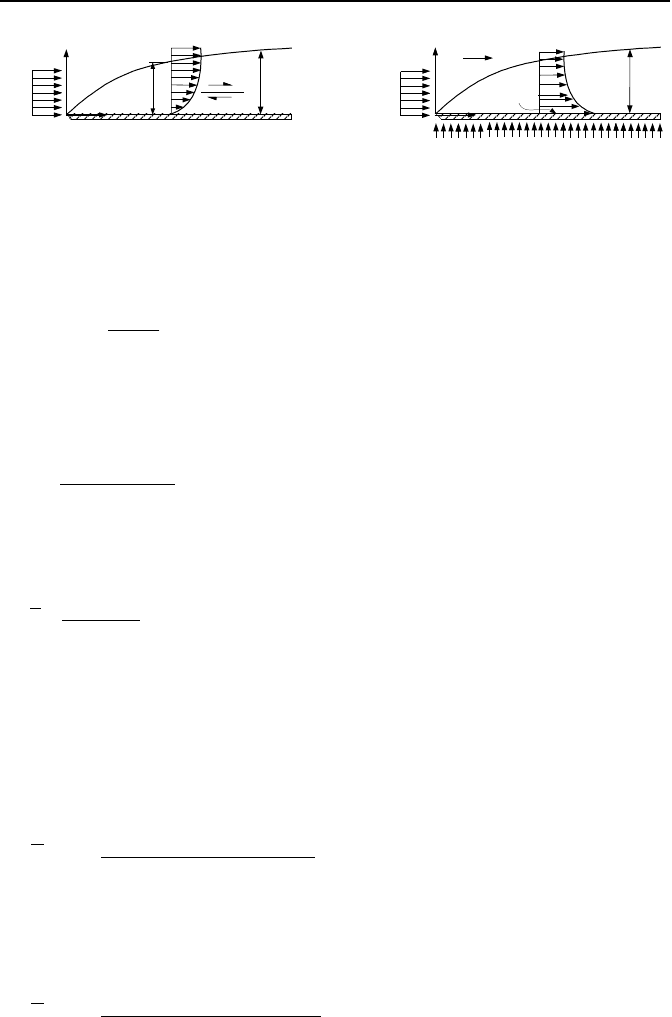
1. Definition of Forced Convection Terms 519

δ'(x)

T(y)

δ(x)

(y)

)

Figure IVb.1.1. Hydrodynamic and thermal boundary layers for flow over a heated flat

plate

∂V

(δ)/∂y = 0. The amount of heat transferred from the flat plate to the boundary

layer at any given x is obtained from the local heat flux by applying Fourier’s law

to the flowing fluid;

)0(

−=

′′



Also from Newton’s law of cooling, we have

′′



= h(T

– T

). Hence, the heat

transfer coefficient h is found by setting the left sides of these two equations equal

to each other:

yTk

−

∂∂−

/)0(

IVb.1.1

Since temperatures are changing with x, then h = f(x). An average value for h is

found from:

dxxh

)(

IVb.1.2

Leading edge of a plate is defined as the location on the plate where x = 0.

Trailing edge of a plate is defines as the location on the plate where x = L with

L being the plate length.

Bulk temperature or the mixing cup temperature for a fluid flowing in a con-

duit is given as:

{}

{

}

{}

cdArV

xrTcdArV

)()(

),()(

)(

IVb.1.3

where A is the flow area. If the conduit is a circular cylinder, then the bulk tem-

perature becomes;

{}

dxcrdrV

xrTcrdrV

))(2(

),()2(

)(

πρ

IVb.1.4

520 IVb. Heat Transfer: Forced Convection

Equation IVb.1.4 indicates that the bulk fluid temperature, being averaged at a

given cross section, varies from cross-section to cross-section along the axis of the

conduit. The inlet temperature of fluid, refers to the bulk fluid temperature enter-

ing a conduit.

Film temperature is an arithmetic average between fluid bulk temperature (T

)

and the surface temperature (T

) (i.e., 2/)(

sfFilm

TTT += ).

Prandtl number, after Ludwig Prandtl (1875–1953), is a measure of diffusion

of momentum, as compared to the diffusion of heat in a fluid. The momentum

diffusion appears as kinematic viscosity and diffusion of heat as thermal diffusiv-

ity. Hence, Pr = v/

= (

)/(k/

) =

/k. Since the diffusion of momentum

and heat are also associated with the thickness of the boundary layer, the Prandtl

number is then a parameter which relates

δ, the thickness of the hydrodynamic

boundary layer to

δ’, the thickness of the thermal boundary layer. See Table A.I.6

for the list and the significance of various dimensionless numbers.

The range of Pr number for some fluids is shown in Table VIb.1.1. For water

temperature in the range of 330 F (165 C)

≤ T ≤ 430 F (221 C), the Prandtl num-

ber for water is about unity, Pr

Water

(T) § 1.

Table IVb.1.1. Range of Pr number for various fluids

Fluid Liquid

metals

Gases Water Light Organic

Liquids

Oils Glycerin

Range of

0.003–0.05 0.7–1 1–13 5–50 50–10000 2E3–

8.5E3

The Pr number for various fluids is given in the tables of Appendix IV.

Nusselt number, after Ernest Kraft Wilhelm Nusselt (1882-1957), is a measure

of the temperature gradient at the surface. Dividing heat flux due to convection by

the heat flux due to conduction, both expressed at the surface, we find:

()

xTk

dxkdT

Conduction

Convection

∆

∆∆

∆

≈

−

∆

′′



This dimensionless ratio shows that for a flat plate, Nu number is a function of the

distance from the leading edge, Nu = f(x). Additionally, at any given x, tempera-

ture ranges from T

to T

. Hence at any x, thermal properties may be evaluated at

the film temperature.

Stanton number is the division of the Nu number by the product of the Re and

the Pr numbers. Therefore, St = Nu/(RePr). Substituting for Nu, Re, and Pr num-

bers in terms of the fluid and the flow properties, we find the Stanton number

given as St = h/(

Eckert number after E. R. G. Eckert, is the ratio of the temperature rise due to

energy conversion to the overall temperature gradient. The Eckert number is then

given by Ec =

TcV

∆/

2. Analytical Solution 521

Reynolds-Colburn analogy is a convenient means of allowing the measure-

ment of heat transfer coefficient from the frictional drag on a flat plate in an adia-

batic process. By using the Reynolds-Colburn analogy, it can be shown that the

friction factor is given as f = 2StPr

2/3

2. Analytical Solution

To find the heat transfer coefficient in forced convection analytically, we have to

limit our analysis to the simplest cases of laminar flow over a flat plate or in con-

duits. Even these seemingly simple cases require the introduction of several sim-

plifying assumptions to enable us to reach a solution. Before embarking on such

analysis, it should be added that the application of such simple cases in practice is

rather limited. However, the advantage of such analytical solutions is that they al-

low us to seek solutions having the same functional relationship for more compli-

cated cases such as those involved in turbulent flow. That is to say that the func-

tional relationship assists us in finding experimentally-based empirical correlation

for cases, which are not amenable to analytical solution.

2.1. External Laminar Flow

Consider the steady laminar flow of an incompressible viscous fluid over a flat

surface (Re < 5E5). If fluid temperature differs from that of the plate then both

hydrodynamic and thermal boundary layers would develop over the plate. Let us

further assume that the plate is isothermal, such fluid properties as k,

, and c

are

independent of temperature, and conduction heat transfer in the fluid in the x-

direction is negligible.

Determination of Velocity and Temperature Profiles for Laminar Flow

over Flat Plate

The governing equation for the hydrodynamic boundary layer is Equa-

tion IIIa.3.20-1, repeated below:

∂

−=

∂

IIIa.3.20-1

If the pressure is also constant throughout the flow, then in the above equation

∂P/∂x = 0. For the temperature boundary layer, the governing equation is Equa-

tion IIIa.3.23-1, also repeated below:

∂

IIIa.3.23-1