Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

532 IVb. Heat Transfer: Forced Convection

The constants of integration c

and c

can be found from the following boundary

conditions. At r = 0, due to symmetry,

∂T/∂r = 0. This results in c

= 0. If tem-

perature at r = 0 is known (i.e., T

= T(r = 0)), then c

= T

. Substituting for c

and c

, temperature profile in the flow is found as:

()

−

∂

max

xCL

IVb.2.16

Given the fluid velocity and temperature at the pipe centerline, we can find fluid

temperature at any cross section for a given axial and radial location by using

Equation IVb.2.16. For example, the wall temperature T

at any axial location is

obtained by setting r = R to find:

()

max

xCLs

∂

However, the most important application of Equation IVb.2.16 is in finding the

fluid bulk temperature. This is obtained by substituting for temperature profile in

Equation IVb.1.4 and carrying out the integrals to find:

()

max

xCLf

∂

IVb.2.17

We now find heat transfer coefficient from the fact that:

Rryfs

rTkyTkTThq

∂∂=∂∂−=−=

′′

)/()/()(



The derivative of temperature in the radial direction is found as (∂T/∂r)

r = R

[(V

)

max

R/4

]∂T/∂x then

RVxT

xTRVk

rTk

)4/())(/)(/1)[(24/11(

/]4/)[(

)/(

max

∂∂

−

∂∂−

IVb.2.18

From h = 48k/11D we find Nu = hD/k = 48/11. Thus, for laminar flow inside

pipes Nu = constant.

The topic of internal flow of fluids in heated conduits is discussed in more de-

tails in Section 2 of Chapters VIa and VIe. Figure IVb.2.2 shows the temperature

profiles for two interesting cases of constant heat flux specified at the channel wall

(Figure IVb.2.2(a)) and an isothermal channel wall (Figure IVb.2.2(b)).

2. Analytical Solution 533

Fully

developed

Entrance

region

(x)

′′

developed

Fully

(x)

Entrance

region

′′

Pipe wall temperature

(a) (b)

Figure IVb.2.2. Axial temperature profiles (a) constant wall heat flux and (b) constant wall

temperature

Example IVb.2.5. Consider the fully developed flow of an incompressible vis-

cous flow at velocity V in a heated pipe of diameter D and length L. Heat flux of

′′



= f(x) is applied to the channel wall. Derive the axial temperature distribution

in terms of

′′



, V , D, L, and

)()( xfxq

′′

Control Volume

Solution: We write the mass and energy balance for the shaded control volume at

steady state condition:

[

]

[]

DdxxqdhDV

ππρ

)()4/(

′′



Since flow is subcooled, dh = c

dT. Substituting and integrating from x = 0 to any

x yields:

sff

dxxqVDTxT

)()/4()0()(

′′



where T

(x) is the fluid bulk temperature. If the function representing the wall heat

flux is specified, we can find T

(x). For a special case of constant wall heat flux,

′′

= constant = q

′′

, we find:

534 IVb. Heat Transfer: Forced Convection

)/4()0()( VxqDTxT

′′



IVb.2.19

Equation IVb.2.19 (Figure IVb.2.2(a)) is applicable to any flow regime whether

laminar or turbulent as long as flow remains subcooled so that T

(x = L) <

sat

system

). In Equation IVb.2.19, for x = L, we have T

= T

(L) confirming that

the results are consistent with an overall energy balance over the tube length:

)(

0==

−=

xLxp

TTcmQ



IVb.2.20

3. Empirical Relations

In Section 2 we were able to find analytical solutions only for such limited cases

as forced convection heat transfer for flow over flat plate and inside conduits. In

these cases, we considered steady and laminar flow. Additionally, we used such

simplifying assumptions as incompressible laminar flow, thermal properties inde-

pendent of temperature, no internal heat generation, and negligible heat transfer

from thermal radiation. Still we had to resort to empirical correlations to increase

the range of applicability of Nu number.

In common practice an ideal situation to satisfy all the required conditions gen-

erally does not exist. While in many cases a steady incompressible flow can be

assumed with approximately constant thermal properties in a specified range of

temperature, flow cannot be guaranteed to remain laminar. Indeed, except in

some special cases, flow is generally turbulent. Fortunately, in the majority of

cases the Nusselt number for forced convection heat transfer in turbulent flow has

the same functional relationship with the Pr and the Re numbers as shown in

Equation IVb.2.11. Thus, all we need to do is to find constants c

, c

, and c

These are generally found in experiments, hence the relations are known as em-

pirical correlations. To demonstrate the relation between theory and experiment,

let’s rearrange Equation IVb.2.11 and take the logarithm of each side of the rear-

ranged formula:

(

)

ReloglogPr/Nulog

This equation shows that the logarithm of (

PrNu/

) is a linear function of the

logarithm of the Reynolds number. This functional relation is verified by variety

of tests using different fluids and pipe diameters.

3.1. External Turbulent Flow over Flat Plates

Assuming a turbulent velocity profile V

/(V

)

= (y/δ)

1/7

, substituting in Equation

IVb.2.5 and integrating, we find the boundary layer thickness for turbulent flow

over a flat plate, heated at the leading edge as:

5/1

Turbulent

Re/37.0į

x= 5E5 < Re

< 1E7 IVb.3.1

3. Empirical Relations 535

Comparing the thickness of turbulent versus laminar boundary layer, given by

Equation IVb.2.4, we find that

Turbulent

= 0.074δ

Laminar

3.0

. Since Re

> 5E5,

then

Turbulent

is at least 4 times thicker than δ

Laminar

. Since turbulence is associated

with the eddy diffusivity, being random fluctuations as opposed to the molecular

diffusion in the laminar flow, the fluid Pr number does not influence the boundary

layer thickness in turbulent flow. This implies that in turbulent flow,

δ = δ’. The

local Nu number is given by:

3/15/4

PrRe0296.0Nu

= 0.6 < Pr < 60 IVb.3.2

and the average Nu number by (Whitaker):

4/143.05/4

)/(Pr)9200(Re036.0Nu

sfL

µµ

−= IVb.3.3

where properties are found at T

except for

, which is found at T

. This correla-

tion is valid for 2E5 < Re

< 5.5E6, 0.7 < Pr < 380, and 0.26 <

< 3.5.

3.2. External Flow over Conduits

We already analyzed external flow over flat plates. There are two more cases to

be considered in external turbulent flow. These are flow over single cylinders and

spheres as well as flow over a cluster of cylinders and spheres. For example, flow

across tube banks is of much interest in heat exchanger technology.

Cross Flow over Cylinders

This includes flow over cylinders with circular or non-circular cross section.

When a fluid flows over curved surfaces, depending on the Reynolds number of

the flow, the boundary layer may become separated from the surface. This phe-

nomenon is too complicated to have analytical solutions. Ironically, the boundary

layer separation occurs mostly at very low to moderate Reynolds numbers (10 –

1000). When Re becomes greater than 3E5, the boundary layer separation is de-

layed. Therefore, for flow over curved surfaces, even for laminar flow we have to

resort to empirical correlations such as that recommended by Whitaker:

(

)

()

25.0

5/23/22/1

/PrRe06.0Re4.0Nu

µµ

+= IVb.3.4

Equation IVb.3.4 is valid for 40 < Re < 1E5, 0.65 < Pr < 300, and 0.25 <

5.2. All properties are found at the free stream temperature except for the

which is developed at the surface temperature.

Example IVb.3.1. The surface of a cylinder (D = 10 cm and L = 20 cm) is main-

tained at 127 C. The cylinder is exposed to the cross flow of air. The air velocity,

temperature, and pressure are 40 m/s, 27 C, and 1 atm, respectively. Assuming a

very low surface emissivity, find the rate of heat transfer by convection.

536 IVb. Heat Transfer: Forced Convection

Solution: We find air properties at T

= 300 K: v = 15.89E-6 kg/m

= 18.46E-6

N·s/m

= 2.3E-6 N·s/m

, Pr = 0.707, and k = 0.0263 W/m·C.

We now find the Reynolds number:

Re = VD/v= 40 × 0.1/15.89E-6 = 251,730

Nu = [0.4 × (251,730)

1/2

+ 0.06 × (251,730)

2/3

] × (5.83)

2/5

× (18.46E-6/2.3E-6)

0.25

§ 1500

h = Nu(k/D) = 1500 × (0.0263/0.1) = 394 W/m

·C.



= h(

DL)(T

– T

) = 394 × (

× 0.1 × 0.2) × (127 – 27) § 2.5 kW.

For non-circular cylinders, we use Table IVb.3.1 as recommended by Jakob.

All properties are found at the film temperature

Table IVb.3.1. Coefficients c

and c

for non-circular cylinders

3/1

PrReNu

(a)

(b)(c)(d)D D D D

0.102 0.246 0.153 0.160

0.675 0.588 0.638 0.638

The range for Re number in Table IVb.3.1 is 5E3 < Re < 1E5 except for case

(d) which the range is 5E3 < Re < 1.95E4.

Flow over Spheres

The Nusselt number over a sphere having diameter D can be found from

Whitaker’s correlation:

(

)

()

4/1

5/23/22/1

/PrRe06.0Re4.02Nu

µµ

++= IVb.3.5

applicable for 3.5 < Re < 8E4 and 0.7 < Pr < 380. The Reynolds number is devel-

oped based on D. All properties are found at the free stream temperature except

for

, which is found at T

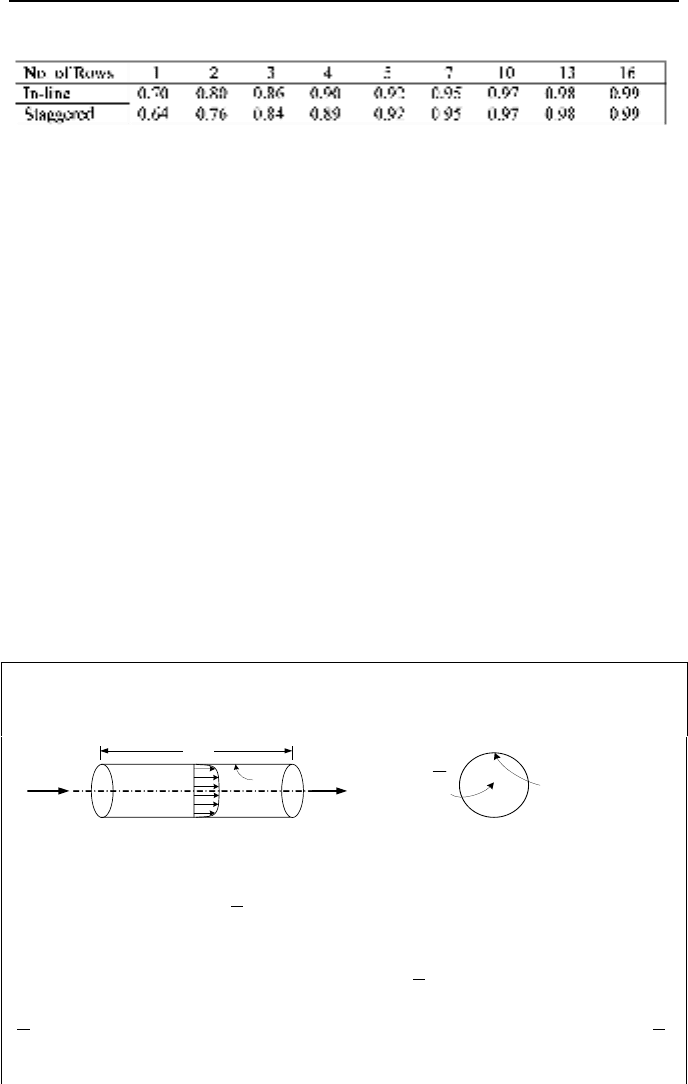
Cross Flow over Bank of Tubes

Shown in Figure IVb.3.1 is cross flow over a tube bank arranged in either in-line

or staggered configuration.

3. Empirical Relations 537

Figure IVb.3.1. Cross Flow over tube banks arranged in in-line and staggered configura-

tions

Note that in both configurations the velocity vector of the fluid flowing over the

tubes is perpendicular to the velocity vector of the fluid flowing inside the tubes.

Our goal is to obtain the heat transfer coefficient for the fluid which is flowing

over the tubes. For the fluid flowing inside the tubes, the heat transfer coefficient

is discussed in Sections 2.2 and 3.3 for laminar and for turbulent flows, respec-

tively. Tubes are spaced by longitudinal pitch (S

) and transverse pitch (S

). Lat-

eral pitch S

is pertinent to the staggered arrangement. Maximum flow velocity

occurs in the gap between the adjacent rods having a height of S

−

D. Form a

mass balance we find V

max

= V

/(S

−

D). The average Nu number is recom-

mended by Zhukauskas as:

25.036.0

max1

)Pr(Pr/PrReNu

IVb.3.6

where c

and c

are given in Table IVb.3.2. This correlation is valid for 0.7 < Pr <

500, 1000 < Re

max

< 2E6, and tubes bundles with 20 or more rows of tubes. If the

number of rows is less than 20, then a correction factor must be used. To apply

the correction factor, the Nusselt number is calculated for a tube bundle with 20

rows of tubes. Then the correction factor C is obtained from Table IVb.3.3 so that

<20

= CNu

All fluid properties in Equation IVb.3.6 are found at the arithmetic mean of the

fluid inlet and outlet temperatures except for Pr

, which is found at the surface

temperature T

Table IVb.3.2. Coefficients in Equation IVb.3.6

Geometry Re

max

10 – 100 0.80 0.40

100 – 1E3 (Treat as a single cylinder)

1E3 – 2E5 0.27 0.63

In-line

> 2E5 0.21 0.84

10 – 100 0.90 0.40

100 – 1E3 (Treat as a single cylinder)

1E3 – 2E5

0.35(S

)

0.2

0.60

1E3 – 2E5

0.40 0.60

Staggered

> 2E5 0.02 0.84

i For S

< 2

j For S

> 2

538 IVb. Heat Transfer: Forced Convection

Table IVb.3.3. Correction factor C for bundles with less than 20 tubes

3.3. Internal Turbulent Flow

A frequently used correlation in internal turbulent flow for single-phase heat trans-

fer is the Dittus-Boelter correlation, originally developed in the 1930s for automo-

tive engineering:

PrRe023.0Nu

8.0

= IVb.3.4

where n = 0.4 if T

> T

and 0.3 if T

< T

. Therefore;

3.08.0

PrRe023.0Nu

= (Fluid is cooled) IVb.3.4-1

4.08.0

PrRe023.0Nu

= (Fluid is heated) IVb.3.4-2

The range of applicability includes 0.7 < Pr < 160, Re

> 10,000, and L/D > 10.

Seider-Tate later modified this correlation for cases with large differences between

the surface and the fluid bulk temperature by accounting for fluid viscosity evalu-

ated at the bulk (

) and at the surface temperature (

14.03.08.0

)/(PrRe027.0Nu

sfDD

µµ

= IVb.3.5

All properties in Equations IVb.3.4 and IVb.3.5 should be found at the fluid bulk

temperature except for

Example IVb.3.2. Water at a rate of 4 kg/s enters a heated pipe at 10 C and

leaves at 30 C. The pipe has a diameter of 5 cm and its wall is maintained at 95 C.

Find the required pipe length.

f 1

f 2

m, c

Solution: To find L, we use Equation IVb.2.20 in conjunction with Newton’s law

of cooling:

(

)

(

)

fsffp

TThATTcm −=−



where T

and T

are the water bulk temperature at the inlet and at the exit of the

pipe. The bulk average temperature is shown by

= (T

+ T

)/2 = (10 + 30)/2 = 20 C. To find A, having



, T

, and

we need to find h:

3. Empirical Relations 539

At 20 C,

= 998.37 kg/m

, c

= 4.18 kJ/kg⋅C,

= 0.001 N·s/m

, k = 0.6 W/m·C,

and Pr = 6.9

Re =

DmVD

µµ



= = 859,101

)4/05.0(001.0

05.04

××

Nu = 0.023Re

0.8

0.4

= 0.023 × 101,859

0.8

× 6.9

0.4

= 505.4 (580 if Equation IVb.3.5

is used)

h = Nu × k/D = 505.4 × 0.6/0.05 = 6065 W/m

·C

A =

(

)

(

)

fsffp

TThTTcm −− /



Substituting values:

A =

DL =

× 0.05 × L = 4 × 4180 × (30 – 10)/[6065 × (95 – 20)]

Solving for the pipe length, we find L = 4.68 m.

Equations IVb.3.4 is applicable to fluids flowing inside conduits. However, the

heat transfer coefficient of water flowing in rod or tube bundles parallel to the axis

of the rods or tubes should be calculated from:

C PrReNu

8.0

= IVb.3.6

where coefficient C is found from:

024.0042.0 −=

Square array (1.1 ≤ s/D ≤ 1.3) IVb.3.7(a)

024.0026.0 −=

Triangular array (1.1 ≤ s/D ≤ 1.5) IVb.3.7(b)

as recommended by Weisman. In these relations s and D are the pitch and the di-

ameter of a tube or a rod, respectively.

Example IVb.3.3. Consider the fully developed flow of water in a rod bundle at a

rate of 2845 lbm/h. System pressure is 1020 psia and water bulk temperature is

525 F. Find the heat transfer coefficient. Use rod pitch = 0.738 in and rod diame-

ter = 0.563 in.

Control

Volume

540 IVb. Heat Transfer: Forced Convection

Solution: We first find the channel flow area and the equivalent diameter:

Flow

= s

– 4(

/16) = 0.738 × 0.738 –

(0.563)

/4= 0.2956 in

= 2E-3 ft

Wetted

= 4(

d/4) =

d = 1.768 in

/2956.0[4=

D 1.768] = 0.668 in

Water properties at P = 1020 psia and T = 525 F are v = 0.02166 ft

/lbm or

46.17 lbm/ft

V = m



A) = (2845/3600)/(47.62 × 2E-3) = 8.08 ft/s

Re =

= [47.62 × 8.08 × (0.668/12)]/(0.23766/3600) = 323,568

Since water is heated up, we use:

4.08.0

PrReNu C

Water

channel

At T = 525 F, we also find Pr = 0.8726 and k = 0.3377 Btu/h·ft·F. Since s/D § 1.3,

C is calculated as:

C = 0.042 × (0.738/0.563) – 0.024 = 0.031055

759)8726.0(568,323031055.0PrReNu

3/18.0048.0

=×=== C

Water

channel

h = Nu × k

Water

= 759 × 0.3377/(0.668/12) = 4606 Btu/h·ft

·F

3.4. Internal Flow of Liquid Metals

An interesting feature of liquid metals, such as bismuth, mercury, and sodium, is

that due to their high thermal conductivity, heat transfer by conduction plays a

much more important role than in ordinary liquids and gases. For liquid metal

properties see Table A.IV.6(SI). Thus, the Nu number for liquid metals includes a

constant, to account for heat transfer by conduction superimposed on the term ac-

counting for flow velocity and hence heat transfer by convection.

For flow in circular tubes, Lyon-Martinelli correlation is recommended for iso-

thermal wall:

Nu = 5.0 + 0.025Pe

0.8

IVb.3.8

where Pe is the Peclet number given by Pe = Re Pr. For uniform wall heat flux,

The Seban-Shimazaki correlation, valid only for s/D > 1.35 is used:

Nu = 7.0 + 0.025Pe

0.8

IVb.3.9

For flow of liquid metals parallel to heated rods, arranged in a hexagonal array,

Dwyer recommends:

Nu = 6.66 + 3.126(s/D) + 1.184(s/D)

+ 0.0155(ψPe)

0.86

Questions and Problems 541

where s/D is the ratio of the pitch to diameter for the array and ψ is given by (La-

marsh and Baratta):

281.1

1.4

)1000Pr(Re/

)/0.942(

−=

QUESTIONS

− What does k in Biot number and in Nusselt number stand for? State the inter-

pretation of each number.

− What is the difference between V

and (V

)

?. Similarly, identify the difference

between T and T

− Which scientist first identified the boundary layer? What is the significance of

the Prandtl number?

− In the analytical derivation of external and internal temperature profiles, we as-

sumed thermal properties to be independent of temperature. Is it then correct to

say that in such circumstance the temperature and the velocity fields are inde-

pendent?

− What is the von Karman method for the development of the energy equation in

the boundary layer?

− How accurate is the thickness of boundary layer obtained from a force balance

in the boundary layer?

− What are the key assumptions, which were made to obtain an analytical solu-

tion for the thickness of the thermal boundary layer?

− Consider heat convection for laminar flow of water in a pipe. What is the ef-

fect of doubling the flow rate on the Nusselt number? What is the effect of us-

ing motor oil instead of water on h?

− What is the difference between the Dittus-Boelter and the Seider-Tate correla-

tions? What is the range of applicability for the Pr number? Are these correla-

tions applicable to liquid metals?

PROBLEMS

1. Start with Equation IVb.2.7 and obtain an approximate relation for the thick-

ness of the hydrodynamic boundary layer. Compare your result with the exact so-

lution.

2. Start with Equation IVb.2.6 and derive a relation for the thickness of the hy-

drodynamic boundary layer by assuming a linear relation for velocity versus dis-

tance, i.e., V

/(V

)

= y/δ.

3. Assume a two-dimensional flow over a flat plate. Use the result of Problem 1

for the thickness of the boundary layer and the velocity profile for V

, as given by