Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


562 IVd. Heat Transfer: Thermal Radiation
Shown in Figure IVd.1.1 is the electromagnetic wave spectrum in terms of
wavelength (
µ
m = 1E-6 m) ranging from about 1E-10
µ
m for high energy cosmic
rays to 1E9
µ
m for low energy electric power. On this spectrum,
γ
rays follow the
cosmic rays. The
γ
rays are emitted directly from the atomic nucleus and their en-
ergy is measured in MeV. For example bombardment of oxygen, O
16
with neu-
trons results in the appearance of unstable nitrogen N
16
, which then decays by
emitting energetic
γ
-rays on the order of 6.13 MeV and 7.12 MeVs. X-rays are
generally less energetic than
γ
-rays and are emitted by atoms while in the excited
state. This is subsequent to an electron dropping to a lower orbit. The ultraviolet
light is much less energetic than X-rays and is harmful only to sensitive tissue.
Generally
γ
-rays, X-rays, and ultraviolet light are of interest to nuclear physicists
and engineers. The visible light covers the small region between 0.4 to 0.7
µ
m.
The monochromatic distribution of visible light is highlighted in figure IVd.1.1.
The region pertinent to heat transfer falls in the 0.1 to 100
µ
m range. This region
includes the low energy portion of ultraviolet, visible light, and entire infrared
spectrum. Microwaves consist of such waves as radar, television, and radio.
Generally, low frequency waves outside the band of thermal radiation are catego-
rized as Hertzian waves and are of interest to electrical engineers.
Wavelength,
λ
in terms of the wave frequency is given as
λ
= c/f where c is the
speed of light and f is the wave frequency. In vacuum the speed of light is c =
2.998E8 m/s. Wavelength is usually expressed in
µ
m.
Planck’s constant, ƫ is the proportionality factor to express wave energy in
terms of the wave frequency. The plank constant is given as ƫ = 6.6256E-34 J·s.
Hence, the wave energy is E = ƫ f, where E is in joules. For example, to find the
radiation energy having a frequency of 0.01
µ
m, we first calculate the wave fre-
quency f = c/
λ
= (2.998E8 m/s)/(0.01E-6 m) = 2.998E16·s
-1
. We then find energy
as E = 6.6256E-34 × 2.998E16 = 1.986E-17 J.
1.2. Definitions Pertinent to Directions and Coordinates
Thermal radiation variables refer to the dependency of the emitted radiation
on the wavelength (referred to as the spectral distribution) and on the direction (di-
rectional distribution).
Spectral distribution refers to the fact that the magnitude of radiation is a
function of wavelength. This is shown in Figure IVd.1.2(a).
Monochromatic radiation emission refers to a radiation at a specific wave-
length.
Directional distribution expresses the fact that surfaces may emit radiation in
preferred directions as shown in Figure IVd.1.2(b). Figure IVd.1.2(c) shows an
isotropic distribution of radiation.

1. Definition of Thermal Radiation Terms 563
λ
Monochromatic
radiation emission
Spectral Distribution
Directional Distribution
(a)
(b)
Isotropic Distribution
(c)
Figure IVd.1.2. Emission of radiation from surfaces (Incropera)
Radiation intensity is an energy density radiated from (emissive) or incident
upon a surface. As we will see in this section, the radiation intensity in general
depends on the wavelength and direction. Therefore, the radiation intensity is ex-
pressed in units of energy per unit time, unit area, unit wavelength, and unit angu-
lar direction.
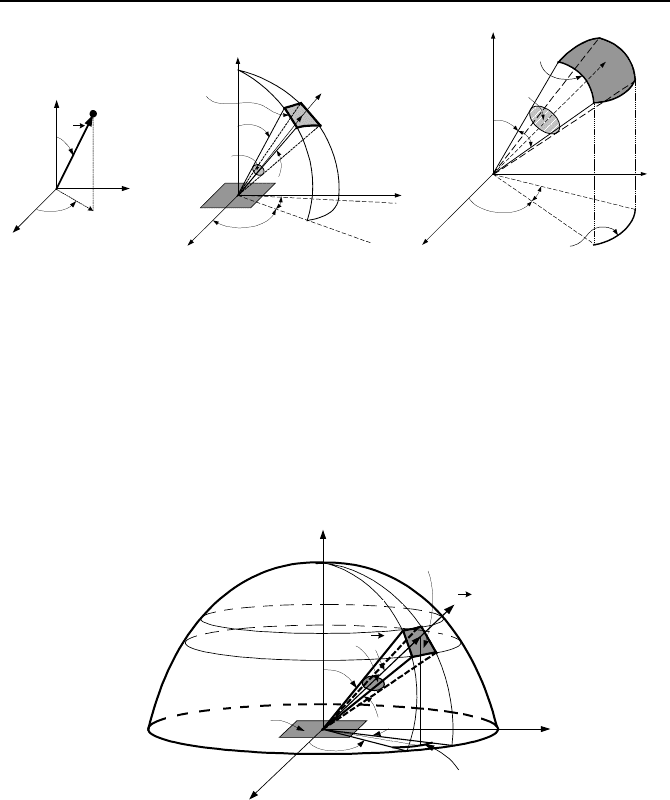
Zenith and azimuthal angles in conjunction with the position vector specify
the location of a point in the spherical coordinate system, Figure IVd.1.3(a). The
zenith angle, measured from the x-axis, is shown by
θ
and is used in polar coordi-
nates. The zenith angle ranges from 0 to 2
π
. The azimuthal angle, measured from
the z-axis is shown by
ϕ
. The azimuthal angle ranges from 0 to
π
/2 for the top
hemisphere (+z). The solid angle, as defined next, ranges from 0 to 2
π
for the top
hemisphere.
Solid angle being a three dimensional angle is defined similar to a two dimen-
sional or a plane angle
*
. To define these angles we consider the spherical coordi-
nate system of Figure IVd.1.3(a). Angles
θ
and
ϕ
are the azimuthal and the zenith
angles (also shown in Figure IVd.1.4). The differential plane angle, such as d
ϕ
in
Figure IVd.1.3(b) or IVd.1.3(c) is defined by the region between two rays of a cir-
cle and is measured as the ratio of the arc between the two rays (dl) divided by the
radius of the circle (r) hence, d
ϕ
= dl/r. We define a differential solid angle in the
same manner. Consider the elemental surface dA
1
as shown in Figure IVd.1.3(b).
Surface dA
1
is defined in spherical coordinates by the azimuthal and the zenith an-
gles
θ
and
ϕ
. The differential surface dA
n
in space subtends a differential solid
angle dΩ when viewed from a point on the differential surface dA
1
. Thus, the
solid angle dΩ is defined by a region between two rays of a sphere and is meas-
ured as the ratio of the differential surface area dA
n
between the two rays divided
by the square of the sphere radius dΩ = dA
n
/r
2
.
*
Solid angle is defined as “the angle formed by the vortex of a cone or subtended at the
point of intersection by three or more planes.” In other words, a solid angle is the angle
intercepted by a cone on a surface of a unit sphere. The unit sphere has a solid angle of 4
π
steradian (sr).
564 IVd. Heat Transfer: Thermal Radiation
x
y
z
r
ϕ
θ
(r,
θ
,
ϕ
)
dA
1
dA
n
ϕ
d
θ
d
ϕ
θ
r
dΩ
dl
d
ϕ =
dl/r
ϕ
d
θ
d
ϕ
θ
rsin
ϕ
d
θ
rd
ϕ
dΩ
(a) (b) (c)
Figure IVd.1.3. (a) Spherical coordinates, (b) and (c) Elemental surface dA
n
subtends
solid angle d
ω
To eliminate the appearance of the arbitrarily taken differential space surface
dA
n
, we may substitute for dA
n
in terms of the spherical coordinate system vari-
ables r,
θ
, and
ϕ
to obtain dA
n
= (rsin
ϕ
d
θ
)(rd
ϕ
). Thus, substituting in dΩ = dA
n
/r
2
we find dΩ = sin
ϕ
d
θ
d
ϕ
. Plane angles have the unit of radians (rad) and solid an-
gles are expressed in units of steradian (sr). Note that 0 ≤Ω≤ 4
π
.
n
r
ϕ
θ
(rsin
ϕ
)d
θ
dΩ
x
y
z
dA
1
dA
n
= [(rsin
ϕ
)d
θ
][rd
ϕ
]
d
ϕ
d
θ
θ
: Azimuthal Angle
ϕ
: Zenith Angle
Ω
: Solid Angle
π
θ
20 ≤≤
2/0
π
ϕ
≤≤
Figure IVd.1.4. Surface dA
n
subtends solid angle dΩ at center of a hemisphere around dA
1
Projected area of surface dA
1
in the direction of n for example is dA
1
cos
ϕ
,
where
ϕ
is the zenith angle (Figure IVd.1.4).
1.3. Definitions Pertinent to Radiation Interaction with a Surface
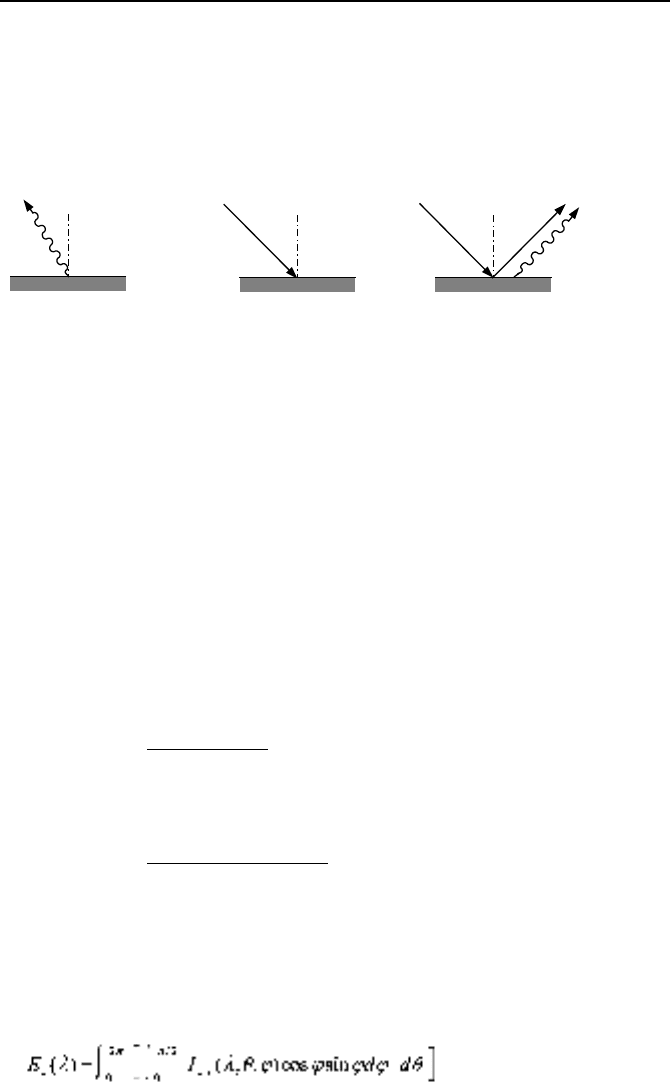
Emission I
e
, refers to the radiant energy emitted by a surface and is identified
here by subscript e, as shown in Figures IVd.1.5(a) and IVd.1.5(c).
1. Definition of Thermal Radiation Terms 565
Irradiation I
i
, is the radiant energy incident on a surface and is identified here
by subscript i, as shown in Figure IVd.1.5(b) and IVd.1.5(c).
Radiosity J
r
, refers to all of the radiant energy leaving a surface (including the
radiation reflected by the surface) and is identified here by subscript r, as shown in
Figure IVd.1.5(c).
{
Radiosity
R
e
f
l
e
c
t
i
o
n
E
m
i
s
s
i
o
n
I
r
r
a
d
i
a
t
i
o
n
E
m
i
s
s
i
o
n
I
r
r
a
d
i
a
t
i
o
n
a b c
Figure IVd.1.5. Depiction of emission, irradiation, and radiosity
1.4. Definitions Pertinent to Emission
Emission spectral intensity, I
λ,ε
(λ,
θ
,
ϕ
) is the rate of emitted radiant energy at
the following characteristics:
− it has wavelength
λ
, per unit wavelength interval d
λ
about
λ
− it travels in the direction of
θ
and
ϕ
and per unit solid angle about this direction.
− it travels per unit area of the emitting surface normal to the direction
θ
and
ϕ
Based on the above definition, if
Qd
is the total rate of energy emitted by the
elemental surface dA
1
, the fraction in the (
θ
,
ϕ
) direction would be Qd
/dA
1
cos
ϕ
.
Of this energy, the portion that is emitted in the interval d
λ
about wavelength
λ
is
Qd
/dA
1
cos
φ
d
λ
. Finally, the portion of this energy passing per unit time in the
solid angle dΩ is
Qd
/dA
1
cos
ϕ
d
λ
dΩ. The spectral intensity has the units of
W/m
2
·
µ
m·sr and is given by
Ω
=
dddA
Qd
I
e
λϕ
φθλ
λ
cos
),,(
1
,
IVd.1.1
Substituting for d
Ω = sin
ϕ
d
θ
d
ϕ
we find:
λϕθϕϕ
φθλ
λ
ddddA
Qd
I
e
sincos
),,(
1
,
=
IVd.1.1
Spectral hemispheric emissive power, E
λ
is defined as the rate of emission of
radiation from a surface per unit surface area, at wavelength
λ
per unit wavelength
d
λ
about
λ
, in all directions. E
λ
has units of W/m
2
·
µ
m. By defining the spectral
hemispheric emissive power, we eliminated the directional dependency:
IVd.1.2
566 IVd. Heat Transfer: Thermal Radiation
Total emissive power, E is the rate of radiation emitted per unit surface area in
all directions at all wavelengths. By this definition, we also eliminated the wave-
length dependence:
³
=
∞
0
)(
λλ
λ
dEE IVd.1.3
Diffuse emitter refers to surfaces that emit radiation isotropically (i.e., inde-
pendent of direction as shown in Figure IVd.1.2(c)). Therefore, in the case of an
isotropic emitter, I
λ
,e
(
λ
,
θ
,
ϕ
) becomes only I
λ,
,e
, which can be removed from the
inside of the integral of Equation IVd.1.2:
)(]4/2cos[)(]2/2sin[)()(
,
2
0
2
0
2/
0,
2/
0
,
λπθϕλθϕϕλλ
λ
ππ
π
λ
π
λλ
eee
IdIddIE =−==
³³³
Total emissive power for a diffuse emitter is calculated from Equation IVd.1.3:
eee
IdIdIdEE
πλλπλλπλλ
λλλ
====
³³³
∞∞∞
0
,
0
,
0
)()()( IVd.1.4
where I
e
is known as the total intensity, having units of W/m
2
·sr and
π
is in sr.
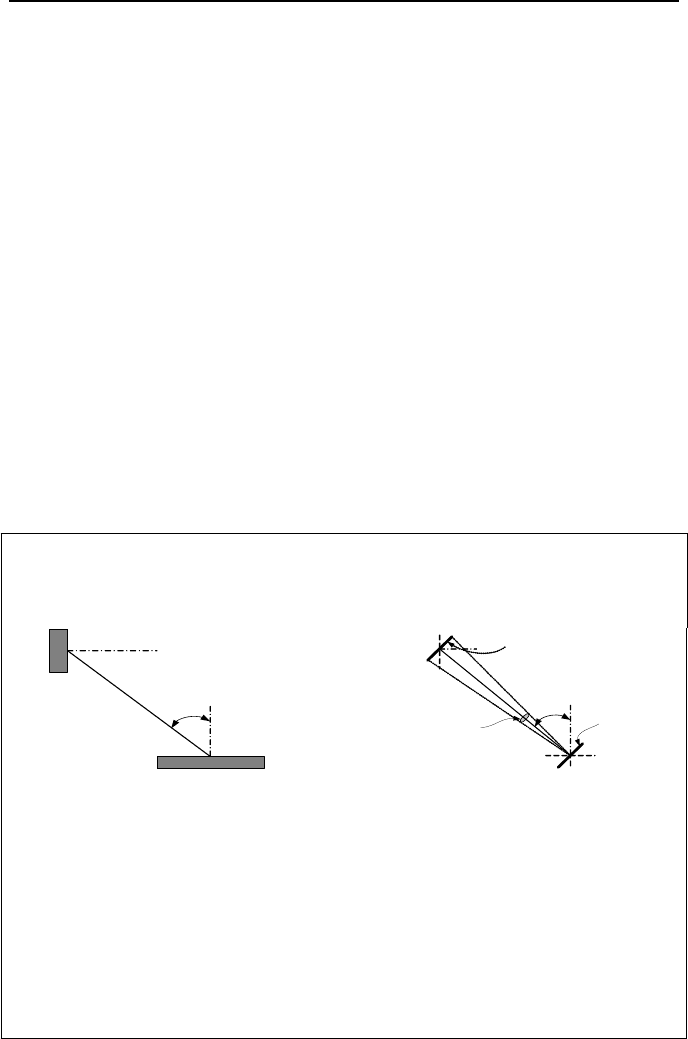
Example IVd.1.1. Surface A
1
is a diffuse emitter with an emission intensity of
8,000 W/m
2
·sr in the normal direction. Find the intensity of radiation received by
surface A
2
for the data given below.
A
1
A
2
ϕ
r
A
1
= 0.002 m
2
r = 0.8 m
A
2
= 0.001 m
2
ϕ
= 75
ο
A
1
cos
ϕ
ϕ
r
A
2
sin
ϕ
dΩ
Solution: Since surface A
1
is a diffuse emitter, the intensity of emission is the
same in all directions including the direction where A
2
is located. Since the given
surfaces are small, we use them as elemental surfaces. To find the solid angle
subtended by A
2
, we use the definition dΩ = dA
n
/r
2
where dA
n
=
dA
2
sin
ϕ.
Substituting, we get dΩ = 0.001 × sin(75
o
)/0.8
2
= 0.0015 sr. The inten-
sity of radiation received by A
2
is given by:
Ω=Ω=
³
∞
ddAIdddAIQd
ee
ϕλϕϕθλ
λ
cos)cos)(,,(
1
0
1,
Qd
= 8000 × [0.0002 × cos(75)] × 0.0015 = 6.2E−4 W.
1. Definition of Thermal Radiation Terms 567
1.5. Definitions Pertinent to Incident Radiant Energy on a Surface
Incident spectral intensity, I
λ,
i
(λ,
θ
,
ϕ
) is the rate of incident radiant energy at
the following characteristics:
− it has wavelength
λ
, per unit wavelength interval d
λ
about
λ
− it travels in the direction of
θ
and
ϕ
and per unit solid angle about this direction.
− it is incident on a surface per unit area of the intercepting surface normal to the
direction
θ
and
ϕ.
Spectral irradiation G
λ
, is the rate at which radiant energy of wavelength
λ
is
incident on the unit area of a surface per unit wavelength interval d
λ
about
λ
.
Spectral irradiation is then related to the spectral intensity:
³³
=
ππ
λλ
θϕϕϕϕθλλ
2
0
2/
0
,
]sincos),,([)( ddIG
i
IVd.1.5
Since the incident spectral intensity has units of W/m
2
·
µ
m·sr, the spectral irradia-
tion has units of W/m
2
·
µ
m.
Total irradiation is that amount of radiant energy incident on the unit area of a
surface in all directions and all wavelengths:
³
∞
=
0
)(
λλ
λ
dGG IVd.1.6
If the incident radiation is diffuse, then the integral of IVd.1.5 can be carried out to
obtain G
λ
(
λ
) =
π
I
λ
,i
(
λ
).
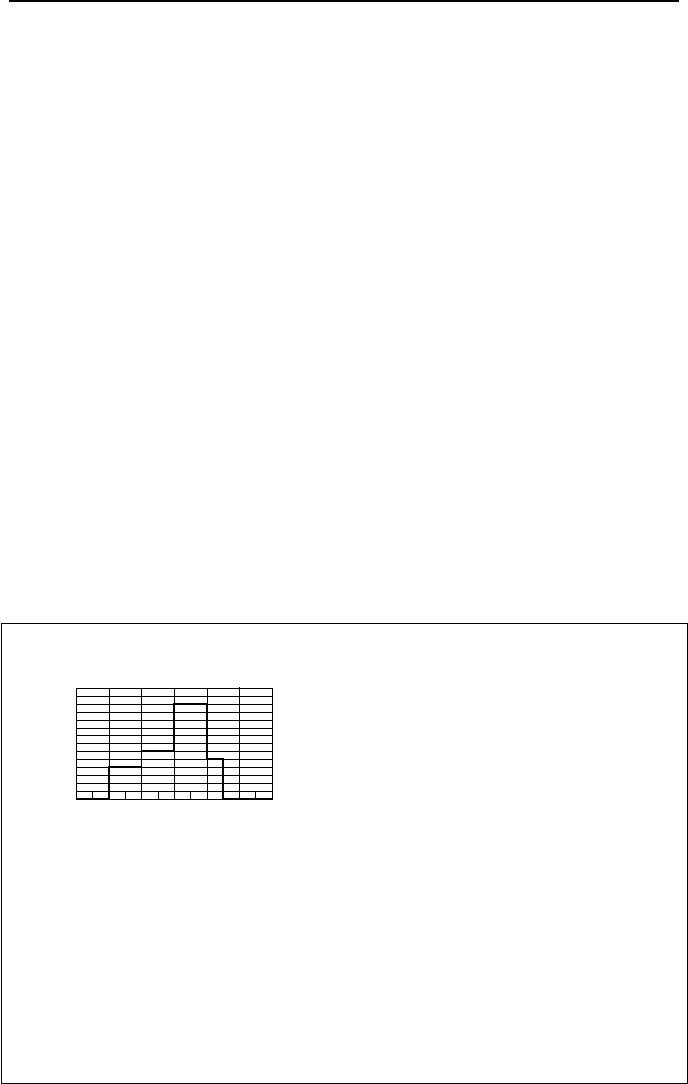
Example IVd.1.1. Find total irradiation and total intensity for the given spectral
irradiation distribution.
0 5 10 15 20 25
1200
λ(
µ
m)
G
λ
,
(
W
/
m
2
.
µ
m
)
30
600
300
900
Solution: We find G from Equation IVd.1.6 by dividing the integral into several
intervals:
³
∞
=
0
)(
λλ
λ
dGG =
³
5
0
0
λ
d +
³
10
5
400
λ
d +
³
15
10
600
λ
d +
³
20
15
1200
λ
d +
³
5.22
20
500
λ
d +
³
∞
5.22
0
λ
d ’
G = 400 × 5 + 600 × 5 + 1200 × 5 + 500 × 2.5 = 12,250 W/m
2
.
Finally, we find total irradiation intensity from I
i
= 12,250/
π
= 3,899 W/m
2
.

568 IVd. Heat Transfer: Thermal Radiation
1.6. Definitions Pertinent to Surface Radiosity
Spectral radiosity, J
λ
(λ) is the rate at which radiant energy of wavelength
λ
per unit wavelength interval d
λ
about
λ
leaves the unit area of a surface. Since
spectral radiosity is the summation of the surface emission and reflection (r) of an
incident radiation and appears in all directions, it has units of W/m
2
·µm:
³³
+
=
ππ
λλ
θϕϕϕϕθλλ
2
0
2/
0
,
]sincos),,([)( ddIJ
re
IVd.1.7
Total radiosity, J is defined similar to the definition of total emissive power
and total irradiation. Thus, total radiosity is the total rate of radiant energy leaving
the unit area of a surface:
³
=
∞
0
)(
λλ
λ
dJJ IVd.1.8
If the surface is a diffuse emitter, then the integral can be carried out to obtain
J
λ
(
λ
) =
π
I
λ,
e+r
(
λ
). Similarly, we find total radiosity given as J =
π
I
e+r
.
2. Ideal Surfaces
In Section 1, we introduced such basic concepts for a surface as emissivity, irra-
diation, and radiosity. In this section, we further explore these concepts by first
treating surfaces as ideal and then as real surfaces.
2.1. Blackbody Radiation
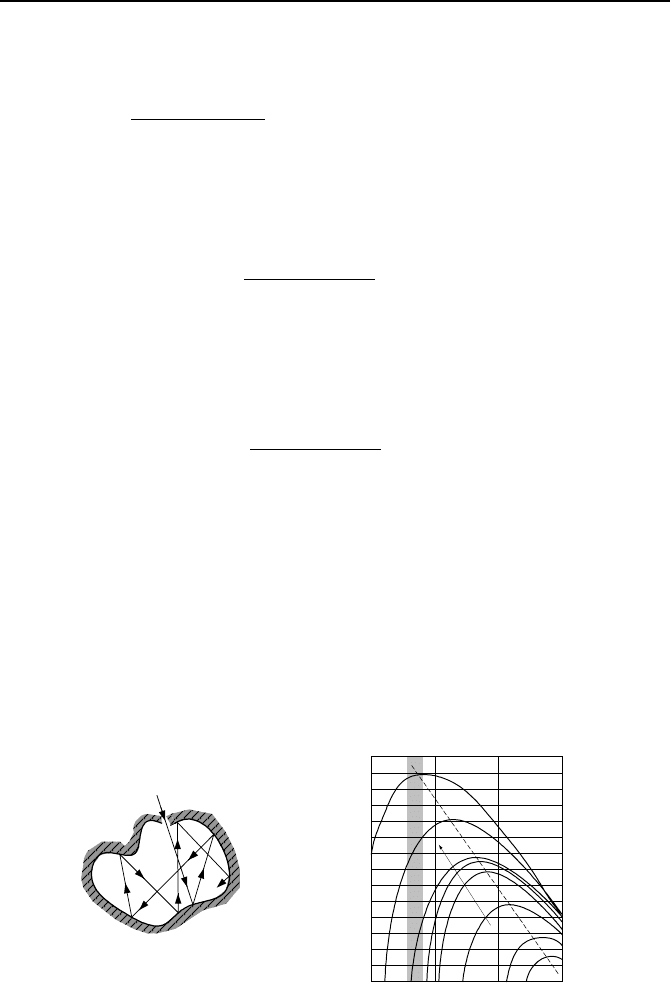
A blackbody is an ideal surface, which satisfies three conditions. First, it is a per-
fect emitter. Thus, for a specified temperature and wavelength, a blackbody emits
more radiant energy than any other surface at the same temperature. Second, a
blackbody is the best absorber of energy. Therefore, it absorbs all energies inci-
dent on it from all directions and at all wavelengths. Third, a blackbody is a dif-
fuse emitter. In other words, the radiant energy emitted from a blackbody is only
a function of temperature and wavelength but is independent of direction. Fig-
ure IVd.2.1(a) shows an isothermal cavity that approaches the definition of a
blackbody.
Historically, Joseph Stefan in 1879 suggested that the total emissive power of a
blackbody is proportional to the fourth power of the absolute temperature. It was
Ludwig Boltzmann who in 1884 applied the principle of classical thermodynamics
to analytically derive the same result. Hence, according to Stefan-Boltzmann:
E
b
=
σ
T
4
IVd.2.1
where
σ
is the Stefan-Boltzmann constant,
σ
= 5.67E−8 W/m
2
·K
4
= 0.1714E−8
Btu/ft
2
·h·R
4
. Note in Equation IVd.2.1, T is the absolute temperature and E
b
is the
total emissive power. To obtain the equation for spectral emissive power in terms
2. Ideal Surfaces 569
of temperature we turn to Max Planck, who in 1901 by treating radiation as “pho-
ton gas”, was able to express I
λ
,b
in terms of wave length and temperature:
1)/exp(
)2(
),(
52
,
−
=
−
Tkc
c
TI
b
λ
λ
λ
λ
=
=
IVd.2.2
In Equation IVd.2.2, ƫ is the Plank’s constant, c is the speed of light in vacuum
and k is the Boltzmann’s constant, k = 1.3805E-23 J/K. Since a blackbody is a
diffuse surface, from Equation IVd.1.4 we find that:
1)/exp(
),(),(
2
5
1
,,
−
==
−
TC
C
TITE
bb
λ
λ
λπλ
λλ
IVd.2.3
where in Equation IVd.2.3, C
1
= 2
π
ƫ c
2
= 3.742E8 W·µm
4
/m
2
and C
2
= ƫc/k =
1.439E4
µm·K. If we integrate Equation IVd.2.3 over all wavelengths we should
obtain Equation IVd.2.1. This is easily verified:
4
0
2
5
1
0
,
1)/exp(
),( Td
TC
C
dTEE
bb
σλ
λ
λ
λλ
λ
≡
µ
¶
´
−
==
∞
−
∞
³
where the Stefan-Boltzmann constant
σ
= f(C
1
, C
2
). Similarly, from Equa-
tion IVd.1.4 we conclude I
b
= E
b
/
π
. We may plot the Planck’s distribution (Equa-
tion IVd.2.3) by choosing a temperature and finding E
λ
,b
for various values of
λ
.
This is shown in Figure IVd.2.1(b). An interesting feature of these plots is that for
a fixed temperature, the emitted radiation is a continuous function of wavelength.
The magnitude of the spectral emissive power of a blackbody increases with the
increasing wavelength until reaching a peak value after which, the magnitude de-
creases with increasing wavelength. Another interesting feature is the fact that as
the surface temperature increases, the peak spectral emissive power shifts towards
shorter wavelengths.
T
λ
E
λ,
b
(a) (b)
Figure IVd.2.1. (a) An isothermal blackbody cavity as an ideal absorber. (b) Planck’s dis-
tribution
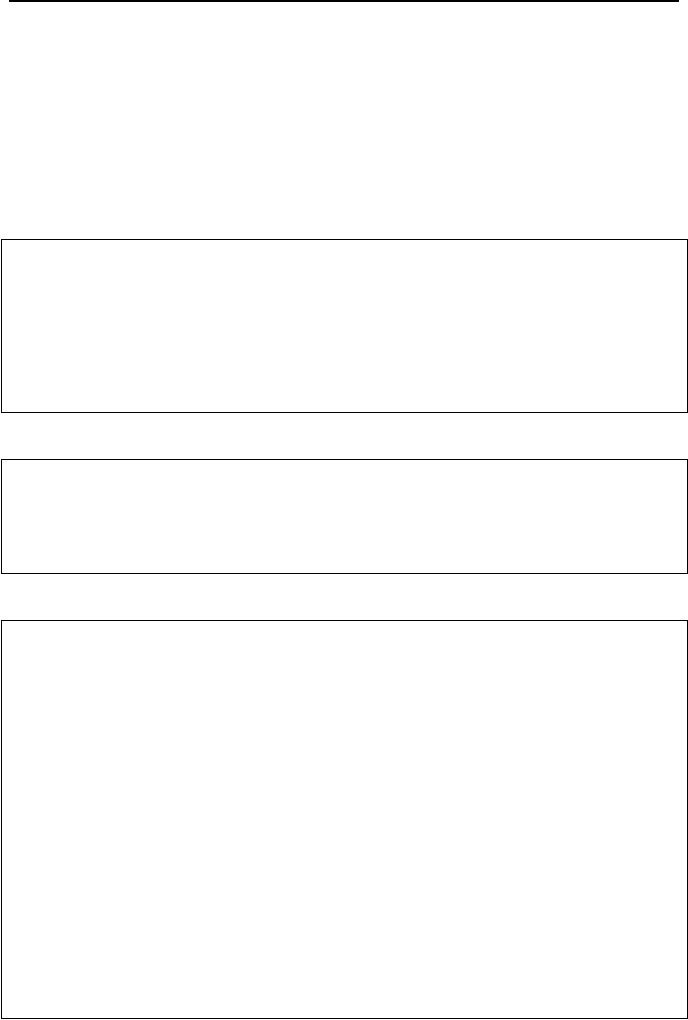
570 IVd. Heat Transfer: Thermal Radiation
The shaded area in Figure IVd.2.1(b) is the visible spectral region. To find the
equation representing the locus of the peak emissive power, we should differenti-
ate Equation IV.2.3 with respect to
λ
and set the result equal to zero. By doing so
we find
λ
max
T = 2897.6 µm·K
This is known as the Wien’s displacement law who derived this equation in 1894.
Example IVd.2.1. The emissive power of a blackbody, at 1
µm wavelength is
measured as 1000 W/m
2
·µm. Find the blackbody temperature.
Solution: We solve Equation IVd.2.3 for temperature to obtain
T =
5
21,
/ln[1 / ]
b
CCE
λ
λλ
−
+ . Substituting, we find
T = 1.439E4
µ
m·K/{1
µ
m× ln[1 + 3.742E8 W/m
2
·
µ
m
4
× (1
µ
m)
-5
/1000 W/m
2
·
µ
m]}
= 1040 K
Example IVd.2.2. The temperature of a blackbody surface is maintained at 3000
K. Find the wavelength associated with the emissive power.
Solution: We use the Wien’s displacement law;
λ
max
= 2897.6/T = 2897.6/3000 =
0.966 µm.
Example IVd.2.3. A metal rod having a length of 1 m and a diameter of 2 cm is
maintained at 150 C (423 K). Fluid flows around the rod at an average tempera-
ture and heat transfer coefficient of 50 C (323 K) and 100 W/m
2
·K. If the rod sur-
face can be approximated as a blackbody, find the percentage of heat transfer by
radiation.
Solution: The amount of heat transfer by forced convection is calculated as:
C
Q
= (
π
Ld)h(T
s
– T
f
) = (
π
× 0.02 × 1) × 100 × (423 – 323) = 628 W
The net rate of heat transfer by radiation from a blackbody is given by:
)(
44
fsR
TTAQ −=
σ
= (
π
× 0.02 × 1) × (5.67E-8) × (423
4
– 323
4
) = 75 W.
The contribution of radiation heat transfer to total rate of heat transfer is about
75/(75 + 628) = 10%.
Contribution of thermal radiation becomes more noticeable as the surface tem-
perature rises.
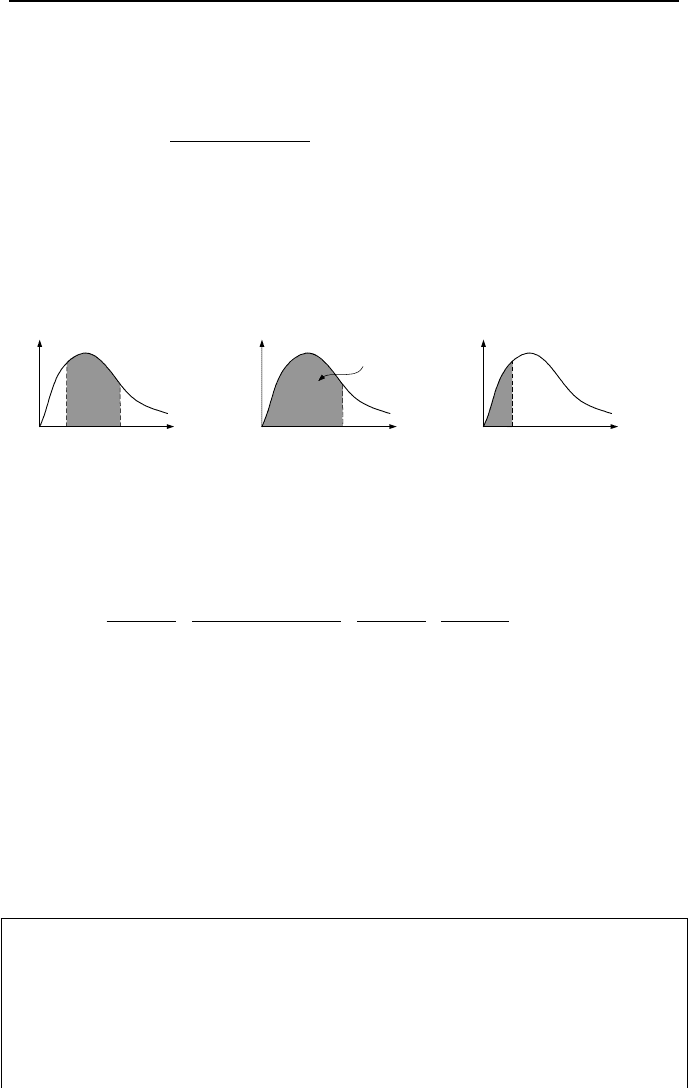
2. Ideal Surfaces 571
Band emission. If we want to know the emissive power in a specific range of
wavelength, say between
λ
1
to
λ
2
, we simply integrate the Planck distribution in
this range:
()
2
12
1
5
1
2
()
exp / 1
b
C
E
d
CT
λ
λλ
λ
λ
λ
λ
−
→
´
µ
µ
µ
¶
∆=
−
IVd.2.4
Often, we are interested in the fraction of the emissive power. For example, if
we want to find the fraction of emission in the range of
λ
1
to
λ
2
, as shown in Fig-
ure IVd.2.2, we integrate Equation IVd.2.3 in this range and divide over the entire
emission, i.e. from zero to infinity.
E
λ
,
b
(
λ
,
T
)
λ
λ
2
= −
E
λ
,
b
(
λ
,
T
)
λλ
1
E
λ
, b
(
λ
, T)
λ
λ
1
λ
2
³
2
0
,
),(
λ
λ
λλ
dTE
b
Figure IVd.2.2. Depiction of band emission calculation
If we show the fraction of emission between
λ
1
to
λ
2
with F( )
21
λλ
→ , then
)0()0()(
12
4
0
,
4
0
,
4
0
,
0
,
0
,
,
21
1212
2
1
λλ
σ
λ
σ
λ
σ
λλ
λ
λ
λλ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
→−→=−=
−
==→
³³³³
³
³
∞
FF
T
dE
T
dE
T
dEdE
dE
dE
F
bbbb
b
b
The integrals of Equation IVd.2.4 are developed between zero to various wave-
lengths and summarized in Table IVd.2.1. The integral representing F(
)0
λ
→ ,
does not have an analytical solution in closed form. However, it may be evaluated
by the following series (Dunkle) in which
ζ
= C
2
/
λ
T:
]6)(6)(3)[()/15()0(
6
1
2344
+++=→
¦
=
−−
ζζζπλ
ζ
iiieiF
i
i
Additional blackbody radiation functions are also summarized in Table IVd.2.1.
Example IVd.2.4. A blackbody is at 5489 C. Find a) the percentage of energy
emitted in the shorter than visible range, b) the percentage of energy emitted in the
longer than the visible range, c) the percentage of energy emitted in the visible
range, and d) the rate of energy emitted in the visible range.
Solution: To find the fractions, we need the arguments,
λ
1
T and
λ
2
T. These are
calculated as:
