Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

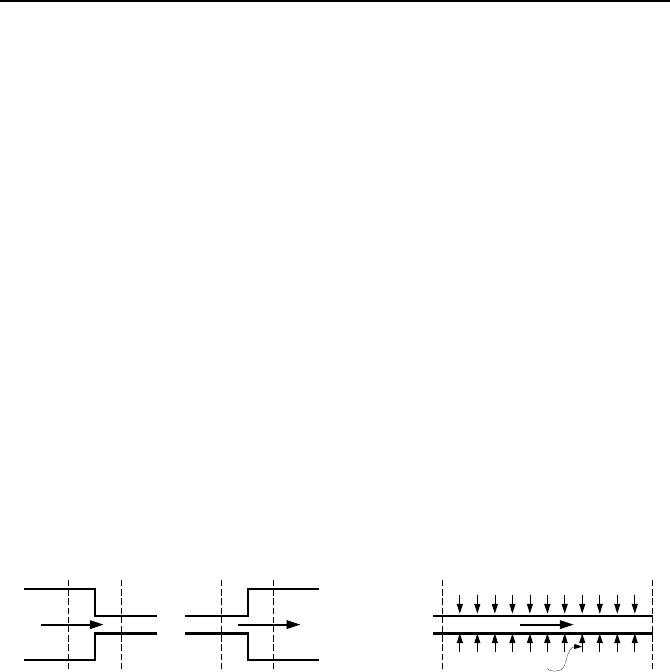
312 IIIb. Fluid Mechanics: Incompressible Viscous Flow
point B. This is calculated based on the elevation of the liquid level in each reser-
voir (measured from the same datum). If the suction reservoir has a higher eleva-
tion than the pump centerline, this term assists the pump head. If there is no pump
and there is no difference in the static pressures between point A and point B, then
there would be a reverse flow if point B is at a higher elevation than point A. Oth-
erwise this term would provide the driving force. The third term in the right side
is the friction pressure drop (
∆P
fric
) which always impedes the flow.
Finally, the fourth term in the right side is the differential pressure term due to a
change in flow velocity. This is either due to change in the flow area (
∆P
vel
) or in
the fluid density (
∆P
acc
). If there is a sudden change in flow area, the associated
frictional loss is accounted for by
∆P
fric
. Hence, ∆P
vel
accounts only for the recov-
erable pressure difference. In this case, as shown in Figure IIIb.4.2, the fluid den-
sities at locations 1 and 2, i.e. before and after the area change, are practically
equal. On the other hand, the flow velocity may change from location 1 to loca-
tion 2 even if the flow area remains the same. This occurs when the fluid flow is
heated up or cooled down. In the case of heat addition,
ρ
2
<
ρ
1
and flow is accel-
erated. If the flow is cooled down,
ρ
2
>
ρ
1
and flow is decelerated. In either case,
the related pressure differential term is referred to as the acceleration pressure dif-
ference. In this chapter, we assume that flow remains single-phase whether heated
up or cooled down. In Chapter Va, we discuss the acceleration pressure difference
for two-phase flow.
1
2
V
12
V
21
ρρ
≅
21
AA ≠
21
ρρ
≅
21
AA ≠
21
Q
.
V
21
AA =
21
ρ
ρ
≠
Figure IIIb.4.2. ∆P
vel
due to sudden area change and ∆P
acc
due to density change
4.1. Types of Problems for Flow in Single-Path Systems
For the single-path system of Figure IIIb.4.1, we can consider a total of 10 vari-
ables: pipe length (L), pipe diameter (D), pipe relative roughness (e =
ε
/D), suc-
tion reservoir pressure (P
1
), discharge reservoir pressure (P
2
), suction reservoir
elevation (Z
1
), discharge reservoir elevation (Z
2
), flow temperature (T, to find
µ
and
ρ
), flow rate ( m
= V
ρ
), and pump head (h
s
) or alternatively pump pressure
rise (
∆P
pump
). Let’s consider a case where 5 of these variables such as L, e, Z
1
, Z
2
,
and T are given. In this case, we can calculate any of the 5 remaining variables if
the other four are also given. This discussion is summarized in Table IIIb.4.1
where 5 arbitrarily selected parameters of L,
ε
, Z
1
, Z
2
, and T are assumed to be
known. Then four types of problems are identified.
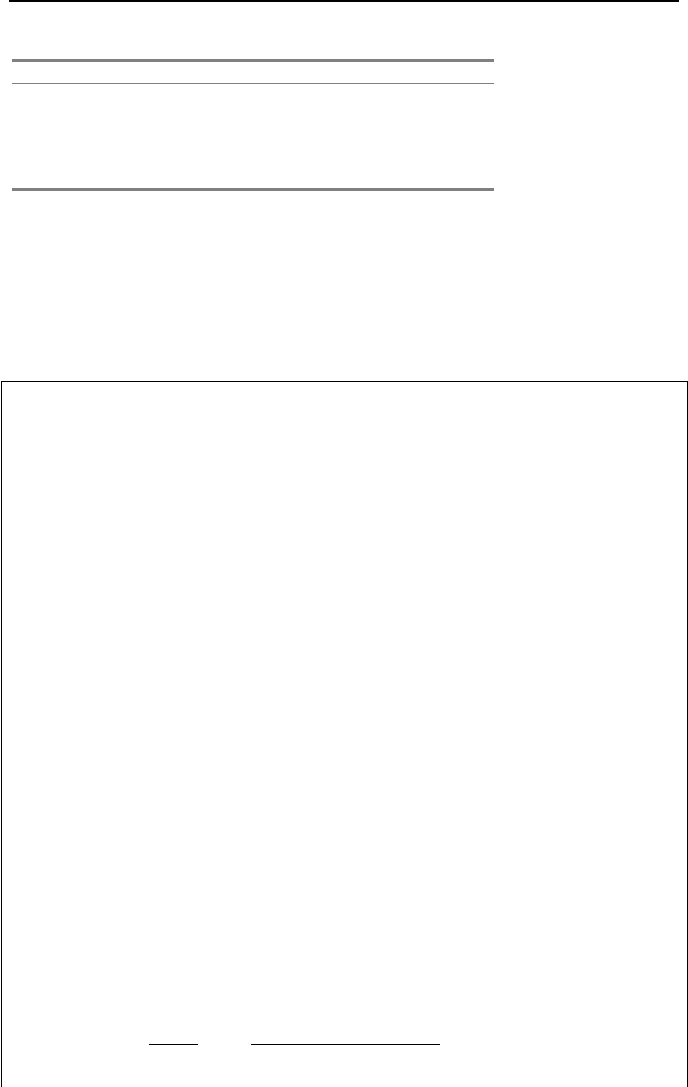
4. Steady Incompressible Viscous Flow in Piping Systems 313
Table IIIb.4.1. Matrix of parameters for given L,
ε
, Z
1
, Z
2
, and T
Type Known Find
I
P
1
, P
2
, D, m
∆P
pump
II
P
1
, P
2
, D, ∆P
pump
m
III
P
1
, P
2
, m
, ∆P
pump
D
IV
D,
m
, ∆P
pump
P
1
(or P
2
)
The following four examples are solved for each of the above four types.
Type I. For Given Data Find Pump Head
Problems in which flow rate and diameter are specified have a straightforward so-
lution as shown below.
Example IIIb.4.1. The following data are given for Figure IIIb.4.1. Find pump
head.
Data: L = 1000 ft (304.8 m), smooth pipe, Z
1
= 5 ft (1.5 m), Z
2
= 100 ft (30.5 m),
water at T = 60 F (15.5 F), P
1
= 15 psia (103.4 kPa), P
2
= 30 psia (206.8 kPa),
D = 4” (10.16 cm), V
= 200 GPM (12.6 lit/s).
Solution: To find the pump head, we need to find the various pressure differential
terms of Equation IIIb.4.1:
D = 4/12 = 0.334 ft
A =
π
D
2
/4 =
π
(0.334)
2
/4 = 0.087 ft
2
(8.08E-3 m
2
)
At T = 60 F,
ρ
= 62.4 lbm/ft
3
(998 kgm
3
),
µ
= 2.71 lbm/ft·h, and v =
ρ
µ
/ =
0.044 ft
2
/h (1.135E-6 m
2
/s)
V
= 200 GPM/7.481 = 26.73 ft
3
/min = 0.445 ft
3
/s (12.6 lit/s). Assuming turbu-
lent flow and using Equation IIIb.3.3, we find:
Re = V
D/vA = 1603.8(0.334)/[0.044(0.087)] = 139,940
f = 0.184/Re
0.2
= 0.184/(139940)
0.2
= 0.017
We now calculate the pressure drop terms:
∆P
grav
= 62.4 (32.2/32.2) (100 – 5) = 5928 lbf/ft
2
= 41.2 psi (284 kPa)
∆P
stat
= 30 – 15 = 15 psia (103.4 kPa)
To calculate ∆p
fric
, we need to find K:
K = K
sharp-edged
+ 4K
90
+ 2K
gate
+ K
check
+ K
globe
+ K
expansion
K = 0.5 + 4(14f) + 2(8f) + 50f + 340f + 1 = 8.5
∆
P
fric
=
()
=
×××
×
»
¼
º
«
¬
ª
+×
2
2
087.04.622.322
445.04.62
5.8
334.0
1000
017.0
10.5 psi (72.4kPa)

314 IIIb. Fluid Mechanics: Incompressible Viscous Flow
Therefore, ∆P
pump
= 41.2 + 15 + 10.5 = 66.7 psi = 154 ft (47 m) of water. We may
also find the pumping power from the pump head:
W
= V
∆P = 0.445 ×(66.7×144) = 15.4E6 ft·lbf/h = 5.8 kW = 7.8 hp
Assuming a pump efficiency of 70%, the required pumping power is 11 hp.
Type II. For Given Data Find Flow Rate
These types of problems generally require iteration. However, this can be avoided
by using a friction factor from Table IIIb.3.2 for a clean commercial steel pipe.
Example IIIb.4.2. The following data are given for Figure IIIb.4.1. Find the
flow rate of water from tank A to tank B. Data: L = 150 m, smooth pipe, Z
1
= −3
m, Z
2
= 15 m, water at T = 15 C, P
1
= 103 kPa, P
2
= 117 kPa, D = 6 cm, pump
head = 37 m, total loss coefficient = 8.5.
Solution: To find the pump flow rate, we find the various pressure differential
terms:
D = 6/100 = 0.06 m
A =
π
(0.06)
2
/4 = 2.83E−3 m
2
At T = 15 C,
ρ
= 1000 kg/m
3
,
µ
= 0.114E–2 N·s/m
2
, v =
µ
/
ρ
= 0.114E–5 m
2
/s
∆P
pump
=
ρ
gh
pump
= 1000 × 9.81 × 37 = 363 kPa
Unlike case A, we do not have the flow rate to calculate the Reynolds number and
hence f. However, to avoid iteration, we may use Table IIIb.3.2 to find f = 0.018.
Next, we calculate all the pressure drop terms:
∆P
grav
=
ρ
g(∆Z) = 1000 × 9.81[15 – (–3)] = 176.6 kPa
∆P
stat
= 117 – 103 = 14 kPa
∆P
fric
= (fL/D)
ρ
2
V
/2A
2
= [(0.018×150/0.06) + 8.5]×1000 × V
2
/[2×(2.83E–3)
2
] =
(3.34E6) V
2
kPa
According to Equation IIIb.4.1:
363 = 176.6 + 14 + (3.34E6) V
2
Solving for the volumetric flow rate we find V
= 7.2E–3 m
3
/s = 7.2 lit/s (114
GPM).
Comment: Using the calculated rate, we find Re = 133,904 and the friction factor
from Equation IIIb.3.6 as f = 0.0174, which is in good agreement (within 5%) with
the value we used from Table IIIb.3.2.
Example IIIb.4.3. Find water flow rate at an average temperature of 60 F(15.5 C)
in the shell-side of the heat exchanger. Use tube length L = 20 ft (6 m), shell in-
side diameter D = 2 ft (0.6 m) , tube outside diameter d = 1 in (2.54 cm), number
4. Steady Incompressible Viscous Flow in Piping Systems 315
of tubes N
tube
= 150, ∆P = 10 psi (69 kPa), and total loss coefficient K = 20.
A
A
Tube Sheet
Shell-side
Tube-side
L
d
D
V
P
.
V
P
.
V
.
V
.
AA View
Solution: We first find the physical properties at the average temperature:
At T = 60 F,
ρ
= 62.4 lbm/ft
3
(998 kg/m
3
),
µ
= 2.71 lbm/ft·h (§ 1089E–6 N·s/m
2
)
Since we want the flow rate in the shell-side, we must calculate the hydraulic di-
ameter;
A
f
=
π
(D
2
– Nd
2
)/4 =
π
(2
2
- 150×0.0833
2
)/4 = 2.32 ft
2
(0.216 m
2
)
P
w
=
π
(D + Nd) =
π
(2 + 150×0.0833) = 45.553 ft (13.88 m)
D
h
= 4A
f
/P
w
= 0.204 ft = 2.448 in = 0.204 ft (6.2 cm)
We now calculate the pressure differential terms:
∆P
pump
= ∆P
grav
= 0
∆P
stat
= P
2
– P
1
= –10 psi (69 kPa)
∆P
fric
= [(fL/D) + K]
2
V
ρ
/(2
2
f
A ) = L’
2
V
ρ
/(2
2
f
A )
where L’ = L + L
e
= L + (D
h
×ΣK)/f = 20 + [(0.204 × 20)/f ]
Substituting in Equation IIIb.4.1, we get ∆P
stat
= P
2
– P
1
= –
2
2
2
'
f
A
m
D
L
f
ρ
The solution to this equation depends on the roughness of the surfaces, which in
turn determines the degree of complexity. If the surface is sufficiently rough for
which an
ε
can be defined, then the above equation should be solved by iteration
with either the Moody chart (Figure IIIb.3.1) or the Colebrook correlation (Equa-
tion IIIb.3.5). Here, we solve the above equation for smooth surface and leave the
solution for a case where for example e
= 0.006 to the reader.
Solution 1: We assume that f is a function of D
h
, from Table IIIb.3.2, f = 0.018
L
e
= KD/f = 20 × 0.204/0.018 = 227 ft. Hence, L’ = L + L
e
= 247 ft (72.3 m)
The mass flow rate is found from Equation IIIb.3.14:
247018.0
)14410(204.02.324.622
32.2
2
×
×××××
=
′
∆
=
Lf
PDg
Am
stat
h
c
ρ
= 1197 lbm/s
(543 kg/s)

316 IIIb. Fluid Mechanics: Incompressible Viscous Flow
Solution 2: If we treat friction factor as f = f(D
h
, Re) then to solve for flow rate,
we should write the friction factor as f = 0.184/Re
0.2
for smooth pipes. Since Re =
ADm
h
µ
/
then
2.02.0
)/(184.0
−
= mDAf
h
µ
. We should substitute f into Equa-
tion IIIb.3.12. Note that we cannot use Equation IIIb.3.13 because we cannot find
L
e
from the given total K. Upon substitution into Equation IIIb.3.12 and rear-
rangement, we obtain:
0.2
2 1.8
21.8
K0.184
0
22
stat
fhf
mmP
ADA
µ
ρρ
+−∆=
IIIb.4.2
Substituting numerical values into Equation IIIb.4.2 we find:
0)14410(
3235.2204.02.324.622
)360071.2(184.0
3235.22.324.622
20
8.1
8.1
2.0
2
2
=×−
××××
××
+
×××
mm
This equation simplifies to 06E562.1335.0
8.12
=−+ mm
. We find by iteration
=m
1200 lbm/s (544 kg/s). This is equivalent to V
= 8,646 GPM (545 lit/s).
Thus the Reynolds number is found as Re = 140193 and f = 0.0172. This shows
that solution 1 provided a reasonably accurate answer while being simpler to carry
out.
Comment: As discussed in Chapter VIa, heat exchangers use baffle plates to hold
tubes in place and prevent flow-induced vibration. An exact value for K is peculiar
to the specific design of a given heat exchanger. It is shown in Chapter VIa, that
design of a heat exchanger is a compromise between both thermal and hydraulic
aspects in addition to other design parameters such as cost, size, material, structure,
and performance. In this problem we dealt with a few parameters such as L,
ε
, ∆P,
D, d, N, K, and V
. The reader may perform a parametric study to see the effect of
each parameter on pressure drop or the flow rate.
Type III. For Given Data Find Pipe Diameter
In problems where the pipe diameter is an unknown, we resort to iteration as
shown in the next example.
Example IIIb.4.4. The following data are given for Figure IIIb.4.1. Find the pipe
diameter.
Data: L = 100 m, Z
1
= 0 m, Z
2
= 25 m, water at T = 16 C, P
1
= 105 kPa, P
2
=
140 kPa, V
= 0.01 m
3
/s, pump head, h
p
= 85 m. The pipe is smooth and K = 8.5.
Solution: To find the pump flow rate, we calculate the ∆P terms for Equa-
tion IIIb.4.1:
At T = 16 C,
ρ
= 1000 kgm/m
3
,
µ
= 0.111E-2 N·s/m
2
, v =
µ
/
ρ
= 0.111E-5 m
2
/s
Since we do not have the pipe diameter, we cannot calculate the Re number and

4. Steady Incompressible Viscous Flow in Piping Systems 317
hence f (or find f) in Table IIIb.3.2. Thus, f remains an unknown, being a function
of pipe diameter, D.
To find D, we proceed as follows:
∆P
pump
= 1000× 9.81×85 = 833.85 kPa
∆P
grav
= 1000× 9.81×25 = 245.3 kPa
∆P
stat
= 140 – 105 = 35 kPa
∆P
fric
= [(fL/D) + K]
2
m
/[2
ρ
(
π
D
2
/4)
2
] = ∆P
pump
– (∆P
grav
+ ∆P
stat
) = c
1
Assuming flow is turbulent, solution to this equation depends on the correlation
we use for f. Let’s use the simple explicit relation given by Equation IIIb.3.6 for
smooth pipes, f = 0.184/Re
0.2
. Substituting for Re = VD/v = V
D/vA = 4 V
/
π
vD, f
= [0.184(
π
v/4 V
)
0.2
]D
0.2
. The above equation then simplifies to:
0K
8.0
3
4
2
=−−
−
DcDc
where )V8/()(
2
1
2
2
ρπ
cc = , Lvc
2.0
3
)V4/(184.0
π
= , and c
1
= ∆P
pump
– (∆P
grav
+
∆P
stat
)
Substituting numerical values, we get:
c
1
= 833.85 – (245.3 + 35) = 553.55 kPa.
c
2
= (3.14)
2
×553.55/(8×1000 ×0.01
2
) = 6829.15
c
3
= 0.184[3.14× 0.111E-5/(4×0.01)]
0.2
×100 = 2.837
Therefore, we should solve (6829.15×1000)D
4
– 2.837D
-0.8
– 8.5 = 0. By itera-
tion we find D ≈ 4.92 cm.
Type IV. For Given Data Find Reservoir Pressure
Solution to these types of problems is straightforward and does not require any it-
eration, as shown next.
Example IIIb.4.5. The steady flow rate of water in the coil from tank A to tank B
is given as 200 GPM (12.6 lit/s). Find the pressure in tank A. The pressure in
tank B is 250 psia (1.72 MPa) and water temperature is T = 100 F (37.8 C).
Solution: To find the pressure in tank A, we use Equation IIIb.4.1 between points
A and B located on the water surface of tanks A and B, respectively.

318 IIIb. Fluid Mechanics: Incompressible Viscous Flow
P
A
P
B
40 ft
10 ft
5 ft
100 ft
60 ft
15 ft
90
o
Threaded
Inside Diameter: 3.55 in
Smooth Pipe
At T = 100 F,
ρ
= 62 lbm/ft
3
(993 kg/m
3
),
µ
= 1.647 lbm/ft⋅h hence, v = 0.0266
ft
2
/h (6.86E–7 m
2
/s).
L = 7 × 100 + 6 × 5 + 40 + 60 = 830 ft (253 m)
D = 3.55/12 = 0.296 ft (0.09 m)
A =
π
D
2
/4 =
π
(0.296)
2
/4 = 0.0687 ft
2
(6.38E–3 m
2
)
Re =
()
3
22
200 60 / 7.481 ft / h 0.296 ft
V
0.0266 ft /h 0.0687 ft
D
vA
××
=
×
= 260,000
f = 0.184/Re
0.2
= 0.184/12.656 = 0.0152
The total loss coefficient is found as:
K = K
enterance
+ K
Check Valve
+ 14K
90 elbow
+ 2K
tee
+ K
Globe Valve
+ K
Gate Valve
+ K
exit
K = 0.5 + (50 + 14×30 + 2 ×20 + 340 + 8) f + 1 ≅ 15
We now calculate the differential pressure terms including ∆P
fric
:
∆P
stat
= 250 – P
A
∆P
grav
= 62×(100 + 15 – 10) = 6510 lbf/ft
2
= 45.2 psi (311.6 kPa)
∆P
fric
=
2
2
K
2
Lm
f
D
A
ρ
§·
+
¨¸
©¹
=
()
2
2
62 200 / 7.481 60
830
0.0152 15
0.296
232.2620.0687
ª ×׺
§·
¬¼
+
¨¸
©¹
×××
=
2333 lbf/ft
2
= 16.2 psi
Substituting into Equation IIIb.4.1 and noting that ∆P
pump
= ∆P
vel-acc
= 0:
(250 – P
A
) + 45.2 + 16.2 = 0
Solving for P
A
, we find: P
A
= 311 psia (2.14 MPa).
The above example provided a situation where the piping does not conform to
Figure IIIb.4.1 yet has a similar solution. The driving force in the above example
was the difference in the static pressures between the supply and the receiving res-
ervoirs. An example in which the driving force is the gravity head follows.

4. Steady Incompressible Viscous Flow in Piping Systems 319
Example IIIb.4.6. A reservoir for water distribution is connected to a 10-cm
pipe. Water surface in the reservoir is 100 m above the pipe. The pipe delivers
water to a point 300 m away from the reservoir. Find the maximum flow rate.
100 m
A
B
10 cm
300 m
Solution: The maximum flow rate occurs when water level is at its highest eleva-
tion and the gate and the globe valves are fully open. We now calculate the pres-
sure terms one by one:
A =
π
D
2
/4 = 3.140×0.1
2
/4 = 7.85E-3 m
2
ABstat
PPP −=∆ = P
atm
- P
atm
= 0
()
ABgrav
ZZgP −=∆
ρ
= 999×9.81(0.0 – 100) = –980,000 Pa
ρ
2
]
11
[
2
22
m
AA
P
AB
vel
−=∆ =
99923E85.7
1
2
2
×
¸
¹
·
¨
©
§
−
m
= 8.12
2
m
Pa
fL/D = 0.017×(100 + 300)/0.1 = 68 (f from Table IIIb.3.2)
K = K
c
+ K
90
+ K
gate
+ K
globe
+ K
e
= 0.5 + (14 + 8 + 340) × 0.017 + 1 = 7.65
2
2
2
)K(
A
m
D
L
fP
fric
ρ
+=∆ = (68 + 7.65)
2
2
)3E85.7(9992 −××
m
= 614.5
2
m
Pa
Substituting into Equation IIIb.4.1 and noting that ∆P
pump
= 0:
–980,000 + (8.12 + 614.5)
2
m
= 0
2
m
=1574 (kg/s)
2
. Thus, =m
39.7 kg/s and V
§ 40 lit/s.
In the above example, we avoided iteration by using f from Table IIIb.3.2. The
next example deals with the acceleration pressure drop.
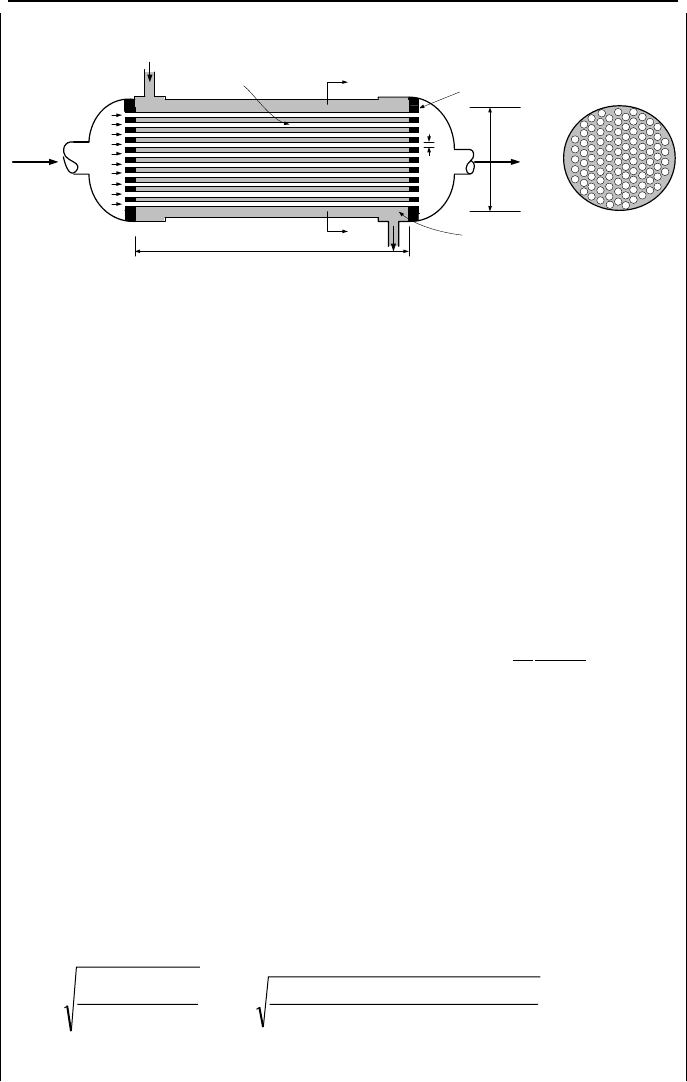
Example IIIb.4.7. Air, at a rate of 12000 lbm/h enters the inlet plenum of a shell-
and tube heat exchanger at14.7 psia and 200 F. Air is heated to 800 F upon leav-
ing the heated section and entering the outlet plenum. Find P
1
– P
4
. Data: N
tube
=
50, tube inside diameter (I.D.) = 1 in, tube length, L = 12 ft. Also D
1
= D
4
= 1 ft.
12 34
Inlet
Plenum
Outlet
Plenum
Tubes
Heated Section

320 IIIb. Fluid Mechanics: Incompressible Viscous Flow
Solution: We note that P
1
– P
4
= (P
1
– P
2
) + (P
2
– P
3
) + (P
3
– P
4
).
We also note that ∆P
pump
= ∆P
grav
= 0.
A
1
= A
4
=
π
(1)
2
/4 = 0.785 ft
2
, and A
2
= A
3
= 50[
π
(1/12)
2
/4] = 0.273 ft
2
K
c
= 0.5(1 – A
2
/A
1
) = 0.5 × (1 – 0.273/0.785) = 0.33
K
e
= (1 – A
3
/A
4
)
2
= (1 – 0.273/0.785)
2
= 0.43
T
= (200 + 800)/2 = 500 F,
µ
air
= 0.068 lbm/h·ft
ρ
2
= (14.7 × 144)/[(1545/28.97) × (200 + 460)] = 0.06 lbm/ft
3
ρ
3
= (14.7 × 144)/[(1545/28.97) × (800 + 460)] = 0.03 lbm/ft
3
V
1
=
11
A
m
ρ
=
785.006.0
3600/12000
×
= 70.7 ft/s, V
2
= 203.5 ft/s, V
3
= 407, V
4
= 142 ft/s
∆P
12
= ∆P
vel
+ ∆P
fric
= 2/)(
2
1
2
22
VV −
ρ
+
2
22
2
2/K Am
c
ρ
∆P
vel
= 2/)(
2
1
2
22
VV −
ρ
= 0.06 × (203.5
2
– 70.7
2
)/(2 × 32.2) = 34 lbf/ft
2
= 0.24 psi
∆P
fric
=
2
22
2
2
K
A
m
c
ρ
= 0.33 ×
2
2
273.02.3206.02
)3600/12000(
×××
= 12.7 lbf/ft
2
= 0.09 psi
∆P
12
= 0.24 + 0.09 = 0.33 psi (2.3 kPa)
For ∆P
23
, Re =
2
A
Dm
µ
=
273.0068.0
)12/1(12000
×
×
= 53870
f = 0.184/Re
0.2
= 0.184/(53820)
0.2
= 0.02
∆P
fric
=
2
2
2
2 A
m
D
L
f
ρ
=
2
2
273.0045.02.322
)3600/12000(
)12/1(
12
02.0
×××
××
= 1 psi
Due to the considerable density change from 2 to 3, we calculate ∆P
acc
:
∆P
acc
=
2
2
2
23
11
A
m
¸
¸
¹
·
¨
¨
©
§
−
ρρ
=
2
2
273.02.32
)3600/12000(
06.0
1
03.0
1
×
¸
¹
·
¨
©
§
− = 0.53 psi
∆P
23
= ∆P
fric
+ ∆P
acc
= 1 + 0.53 = 1.53 psi = (10.5 kPa)
∆P
34
= ∆P
vel
+ ∆P
fric
= 2/)(
2
3
2
43
VV −
ρ
+
2
33
2
2/K Am
c
ρ
∆P
vel
= 2/)(
2
3
2
4
VV −
ρ
= 0.03 × (142
2
– 407
2
)/(2 × 32.2) = –67.7 lbf/ft
2
= –0.47
psi
∆P
fric
=
2
33
2
2
K
A
m
e
ρ
=
2
2
273.02.3203.02
)3600/12000(
43.0
×××
×
= 33.2 lbf/ft
2
= 0.23 psi
∆P
34
= –0.47 + 0.23 = –0.24 psi
P
1
– P
4
= ∆P
12
+ ∆P
23
+ ∆P
34
= 0.33 + 1.53 – 0.24 = 1.62 psi (11 kPa).
Problems involving flow in single-path systems can be easily solved by using the
software on the accompanying CD-ROM.
4. Steady Incompressible Viscous Flow in Piping Systems 321
4.2. Application of Bernoulli Equation in Flow Measurement
Flowmeters are discussed in Chapter VIb. Our purpose here is to demonstrate one
of the practical applications of the Bernoulli equation. In Example IIIa.3.18, we
showed that a reduction in flow area results in the conversion of some pressure
head to velocity head. By measuring the induced pressure difference we then cal-
culated the volumetric flow rate (Equation IIIa.3.48). Depending on the manner in
which the reduction in flow area is introduced, the device is called either venturi,
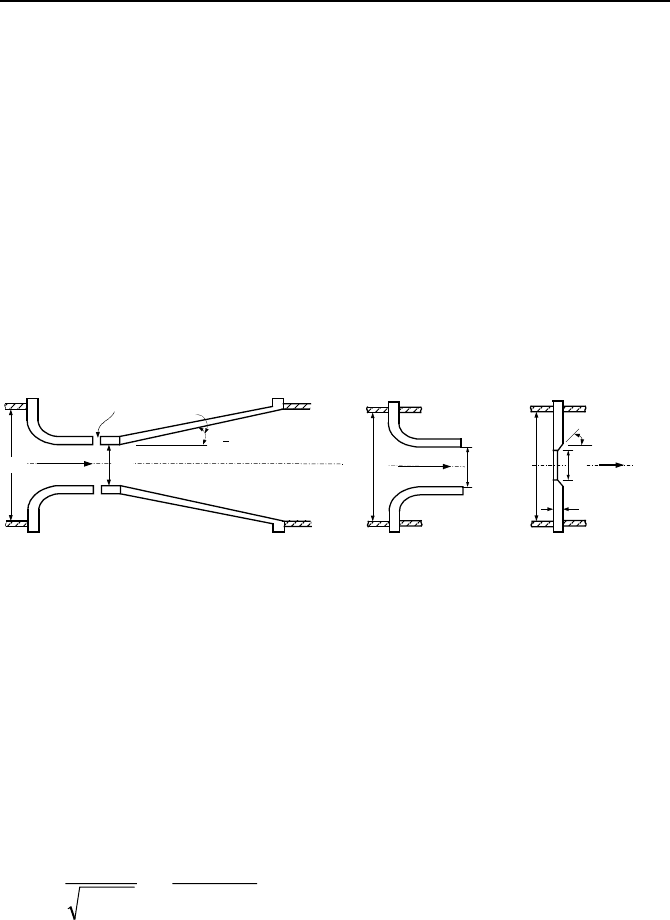
nozzle, or thin-plate orifice. The schematic of these devices is shown in Fig-
ure IIIb.4.3. As seen in this figure, the smoothest reduction in flow area, hence the
least unrecoverable pressure drop takes place in a venturi. This is in contrast to a
thin plate orifice, with the most abrupt change in flow area, introducing the largest
pressure drop. By comparison, the flow nozzle causes a medium pressure drop.
Since these devices are based on the Bernoulli equation and used invasively to
measure the flow rate, we refer to them as the Bernoulli-obstruction meters.
θ
< 15
ο
Throat tap
d
t
D
1
Flow
Cone angle
D
1
Flow
d
t
D
1
Flow
d
t
45
o
- 60
o
0.05D
Venturi Nozzle Thin Plate Orifice
Figure IIIb.4.3. Standard shapes of various Bernoulli meters
Returning to Example IIIa.3.18, we concluded that for a frictionless venturi and
an ideal fluid, flow rate can be measured from the recoverable pressure drop. In
common practice however, we deal with real fluids. Hence, we must account for
the non-recoverable pressure drop due to the frictional losses. This is generally
accounted for by multiplication of the flow rate by a parameter known as the dis-
charge coefficient, C
d
< 1. Therefore, in common practice, the volumetric flow
rate through such devices is calculated from a relation similar to Equa-
tion IIIa.3.48 but with some modifications as follows:
2/1
21
2
4
)(2
1
V
¸
¸
¹
·
¨
¨
©
§
−
−
=
ρ
β
PP
A
C
d
IIIb.4.3
where
β
is the ratio of the diameter of the reduced area (throat) to the pipe di-
ameter (
β
= d
2
/D) and A
2
is the flow area at the throat as shown in Figure IIIb.4.4.
For venturi meters, depending on the Reynolds number, C
d
is in the range of 0.8 ≤
C
d
< 1.0 and for orifice meters in the range of 0.6 ≤ C
d
< 0.95. Note that in the
case of the thin-plate orifice, the flow area is further reduced due to the formation
of vena contracta (also see Figure IIIb.3.2 for sudden contraction).
