Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer

Подождите немного. Документ загружается.

282 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

52. Express the first law as is given by Equation IIIa.3.12 in terms of the enthalpy

of the control volume.

53. Use Equation IIIa.3.23 to derive the rate of change of entropy for a Newtonian

fluid as:

∇

54. Use the velocity profile of Problem 6 for laminar flow between two parallel

plates to find the temperature distribution in the flow in terms of T

, the plates

temperature.

Section 3 (Fluid Rotation)

55. Derive the relation for angular velocity in terms of the velocity components

for fluid rotation in a two-dimensional flow field. [Hint: Use the schematic for ro-

tation in Figure IIIa.3.5 and find the angular velocity for line oa as

= d

/dt.

Substitute for d

= dl

/dx and for dl

from dl

= (∂V

/∂x)dxdt. Do the same for line

ob to find

. The z-component of rotation vector is the average of

and

Do the same for x- and y- components].

56. Show that the convective acceleration for an irrotational flow is given by

(

)

2/VV

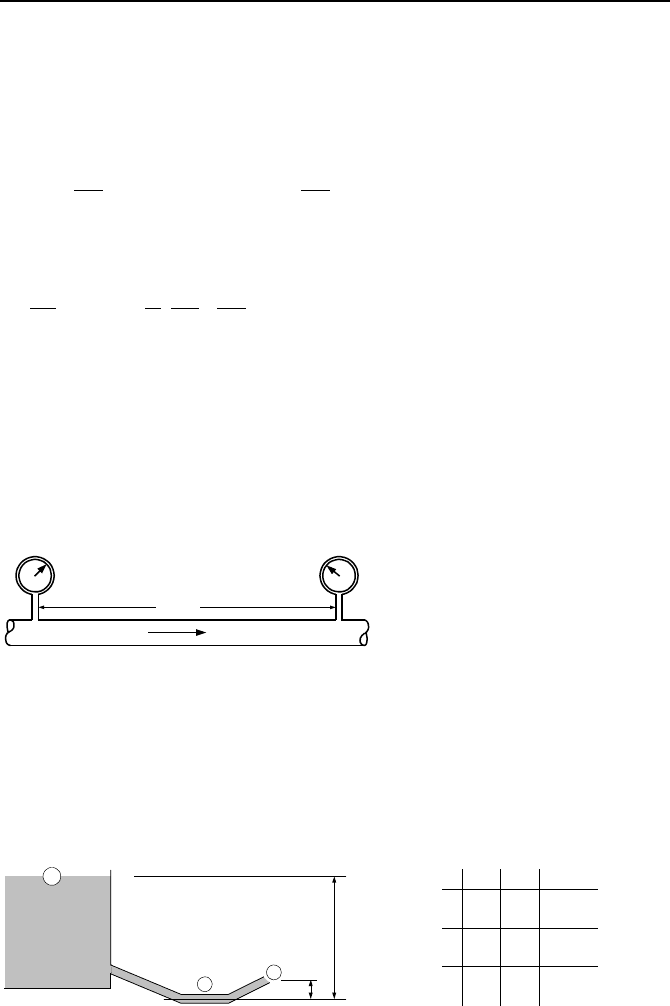
⋅∇ . [Hint: Expand the realtion for convective accelaration

(

)

VVa

∇⋅=

and set the curl of the velocity vector equal to zero].

57. Use the definition of vorticity (

) to find the value of

()

rdV

⋅×

where V is

the velocity vector and dr is an element of length of a stramline. [Ans.: 0].

58. The two components of the velocity vector are given as V

= –ay/(x

+ y

)

1/2

and V

= ax/(x

+ y

)

1/2

where a is a constant in cm/s. Find the vorticity of a fluid

element located at x = y = 1 cm. [Ans.: 1.41a

59. An area closed by the contour C in a flow field is shown in the figure.

Circulation is defined as the summation of the tangential velocity componnet

around the contour C:

VdlΓ=

⋅

Area A

Contour C

a) Find the units of circulation Γ and b) show that

AdV

⋅×∇=Γ .

Questions and Problems 283

Section 3 (Bernoulli Equation)

60. Flow is pumped from point A to point B in a steady state steady flow process.

Start with Equation IIIa.3.12 and obtain the governing equation as given in Equa-

tion IIIa.3.31. [Hint: Equation IIIa.3.12 for steady state steady flow with one inlet

port and one outlet port becomes;

+++=+

esi

hwqgZ

Substituting for h = u + Pv, noting that u

= u

, and rearranging we obtain:

pfei

hh)()

(

)(

−=−−+−+−

where q in Equation 1 is the heat produced by frictional losses and delivered from

the control volume to the surroundings. Also w

in Equation 1 is the shaft work

delivered to the control volume as pump head hence, carrying a minus sign in

Equation 2].

61. An inviscid fluid flows steadily at low speed in a horizontal and well-insulated

pipe.

a) Consider locations a and b along the length of the pipe and chose the correct

answers for velocity (V), pressure (P), and temperature (T):

< V

, V

= V

, V

> V

< P

, P

= P

, P

> P

< T

, T

= T

, T

> T

b) Answer the same questions but for the pipe oriented so that Z

> Z

c) Answer the same questions but for the pipe oriented so that Z

< Z

62. A large reservoir is connceted to a frictionless flow path, having a small flow

area, as shown in the figure.

K.E.

P.E. K.E + P.E.

Specify the kinetic energy, potential energy, and total energy for points A, B, and

C located on the flow path.

284 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals

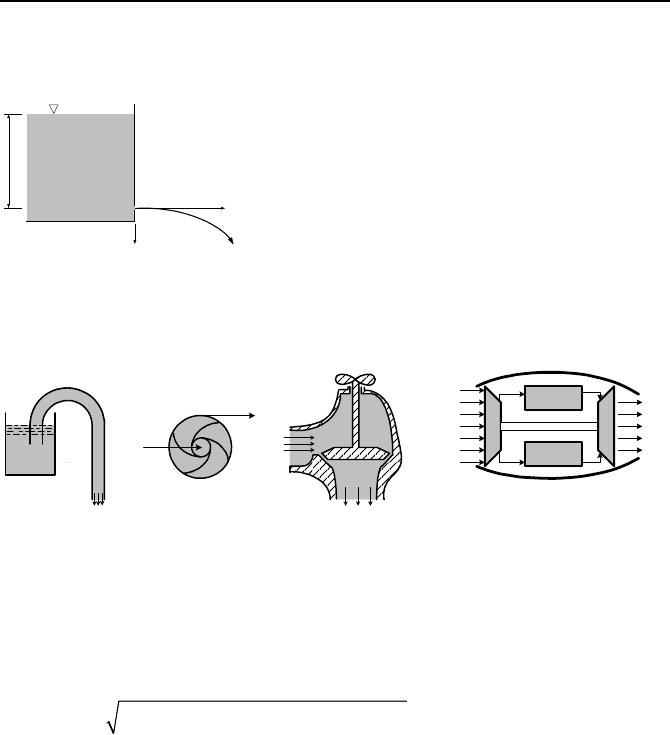
63. Water is flowing out of a small hole located at a depth of h below the free

surface of a large reservior. Find the equation of the stream leaving the hole in the

coordinate shown in the figure. [Ans.: y = x

/4h].

64. Four cases are shown in the figure: water flowing through a smooth siphon,

water flowing through a pump, water flowing through an angle valve, and air flow-

ing through an operating turbo jet. Identify the case to which the Bernoulli equa-

tion is applicable between locations 1 and 2.

C: Compressor

CC: Combustion Chamber

T: Turbine

For cases that the Bernoulli equation is not applicable, specify the alternative equa-

tion that should be used.

65. A turbine (see the figure of Example IIIa.3.21) is located at an elevation H

from the surface of a lake with the discharge pipe located at an elevation H

from

the turbine centerline. Find flow velocity, V

in terms of H

, H

, P

, h

, and

where subscript 4 refers to the discharge piping.

[Ans.:

()

41414

2/ h

VPPgZZ

ρρ

ªº

=−+−−

¬¼

66. A turbine is operating at 150 ft below the surface of a lake. Flow rate of water

through the turbine is 100 ft

/s. The discharge pipe is located 10 ft above the

turbine. In the discharge pipe, where velocity is 25 ft/s, pressure is measured as 12

psig. Find the maximum power developed by this turbine. [Ans.: 1164 hp].

67. A turbine is located 100 m below the surface of a lake. The discharge pipe

has an elevation of 5 m from the turbine centerline. The head developed by the

turbine is 81.5 m. Pressure at the discharge pipe is 15 psig. Find flow velocity

and the power developed by the turbine. Ignore frictional losses and use D

= 4 m.

[Ans.: V

= 7.62 m/s, 76.5 MW].

68. Water at a rate of 1 m

/s enters a small hydraulic turbine from the horizontal

supply line, having a diameter of 50 cm. The pressure at the inlet (stage 1 in the

figure) is 200 kPa. Pressure in the turbine discharge conduit (the draft tube) at

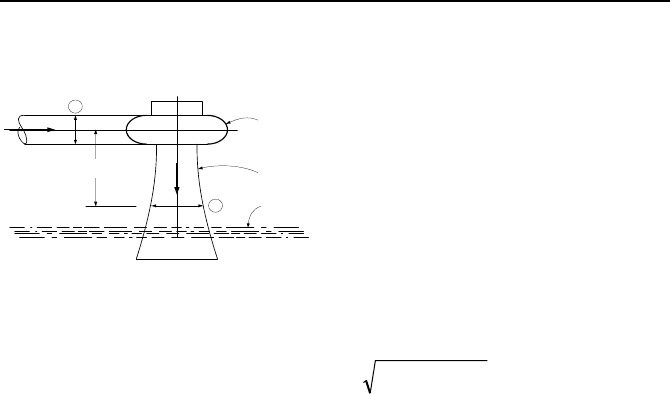
Questions and Problems 285

location 2, which is 2 m below the turbine centerline, is measured as 55 kPa. Find

the shaft head and the horsepower developed by this turbine. Use D

= 65 cm.

Hydraulic

Turbine

Draft Tube

Tail Water

69. Consider the hydraulic jump as shown in Figure IIIa.3.7. Use the continuity

and the momentum equations to derive a relation for z

in terms of V

and z

[Hint: Cancel V

between the two equations, then cancel out (z

– z

) to obtain

121

=−+ azzzz ]. [Ans.: ;)2/()2/(

112

azzzz ++−= where gVa 2/

= ].

70. A siphon (an inverted U-tube) is used to steadily withdraw water from a large

reservoir. The top of the siphon is 1.5 m higher than the surface of the water in

the reservoir and the discharge side of the siphon is 8 m below the water surface.

Ignore all frictional losses in the siphon. Find a) the mass flow rate of water dis-

charged to the atmosphere and b) the pressure at the top of the siphon. Water is at

T = 27 C and 1 atm. The diameter of the siphon tube is 5 cm. [Ans.: a) 24.6 kg/s

and b) 7.86 kPa].

71. In Problem 70, find the hight of the top of the siphon at which pressure

reaches the vapor pressure of the water in the reservoir and the flow becomes dis-

rupted.

72. A pipe is connected vertically to the discharge side of a pump. The top of the

pipe is a short horizontal segment connected to a nozzle. The vertical length of

the pipe (i.e., from the pump discharge to the horizontal segment) is 12 ft long and

the pipe diameter is 4 in. The nozzle discharges water to the atmosphere at a ve-

locity of 65 ft/s. Ignore all frictional losses and find the required pressure at the

pump discharge.

286 IIIb. Fluid Mechanics: Incompressible Viscous Flow

III

. Incompressible Viscous Flow

In the previous chapter, we used Newton’s second law of motion to obtain both

the integral and differential forms of the momentum equation. In this chapter, we

focus on the one-dimensional internal incompressible viscous flow. We use New-

ton’s second law to find the frictional losses associated with the flow of fluids in

pipes, fittings, and valves in steady state conditions. We then conclude this chap-

ter with the study of unsteady state incompressible fluid flow.

1. Steady Incompressible Viscous Flow

Incompressible inviscid flow is a special case for which even analytical solutions

in closed form can be obtained if the flow is also irrotational (known as potential

flow). For incompressible viscous fluids, the task of analyzing the flow is still

well developed provided the flow remains laminar. If the flow is turbulent, the

traditional techniques need to be enhanced by experimental data. Hence, due to

the complexity of turbulent flow, the existing theories are semi-empirical. As

shown in Figure IIIa.1.5, turbulent flow is subject to large lateral fluctuations.

The term turbulent stands for the chaotic nature of the fluid motion, which in-

volves lateral mixing superimposed on the motion of the main stream. The cross-

wise mixing causes additional shear stresses and friction, which results in addi-

tional energy loss for turbulent flow compared with laminar flow. The momentum

transfer by crosswise mixing is shown in Figure IIIb.1.1.

Figure IIIb.1.1. Momentum transfer in turbulent flow

Two particles of fluid having masses m

and m

are exchanged due to the turbu-

lent fluctuations in a flow. In this process, due to the continuity equation, no net

mass is exchanged but the momentum transfer is equal to

)]()([ aVbVm

− where

m = m

= m

and

V represents the average velocity. Next, we investigate the

modification of the conservation equations to account for such momentum transfer

due to the turbulent fluctuations.

1. Steady Incompressible Viscous Flow 287

Modification of Conservation Equations to Accommodate Turbulent Flow

Viscous Newtonian fluids follow Newton’s law of viscosity for laminar flow. In

turbulent flow as explained above, the shear stress is enhanced due to the exis-

tence of the local momentum transfer between the layers of the fluid. The best de-

scription for turbulent phenomena is offered by Hines, “turbulence may be defined

as an irregular condition of flow in which various quantities show a random

variation with time and space, so that statistically distinct average values can be

discerned.”

The Navier-Stokes equations are valid for laminar flow. The difficulty in ap-

plying these equations to turbulent flow lies in the fact that the variables in these

equations refer to the instantaneous values at the point under consideration. Rey-

nolds modified the Navier-Stokes equations so that the variables would be time

averaged. Additional terms were introduced to account for fluctuations in flow.

Scores of experiments have shown that turbulent fluctuations are randomly dis-

tributed. Hence, the frequency spectrum of the fluctuations shows continuous

variations with no peak, as discrete peaks imply periodicity. Mathematically, this

means that the time average of the fluctuating velocity is zero.

dtV

To modify the conservation equations, each laminar term in the equation is re-

placed by the turbulent equivalent such as

xxx

VVV += ,

yyy

VVV += ,

zzz

VVV += , '

+= , etc. These are then integrated over the domain of in-

terest (

) noting that for V

, for example:

xxxx

VdtVVdtV =+=

³³

θθ

)(

This is known as the Reynolds rule of averages. To apply this to the conservation

equation for mass, we note that the equation for steady incompressible flow is

given as:

∂

Substituting terms and integrating yields:

xzxz

VVVV

xyz xyz

§·

¨¸

©¹

∂∂

∂∂∂∂

++ =++=

∂∂∂ ∂∂∂

Therefore, the conservation equation of mass is directly applicable to both laminar

and turbulent flows. Let’s try the same procedure for the conservation equation of

momentum (Equation IIIa.3.17):

VgP

∇++∇−=

µρρ

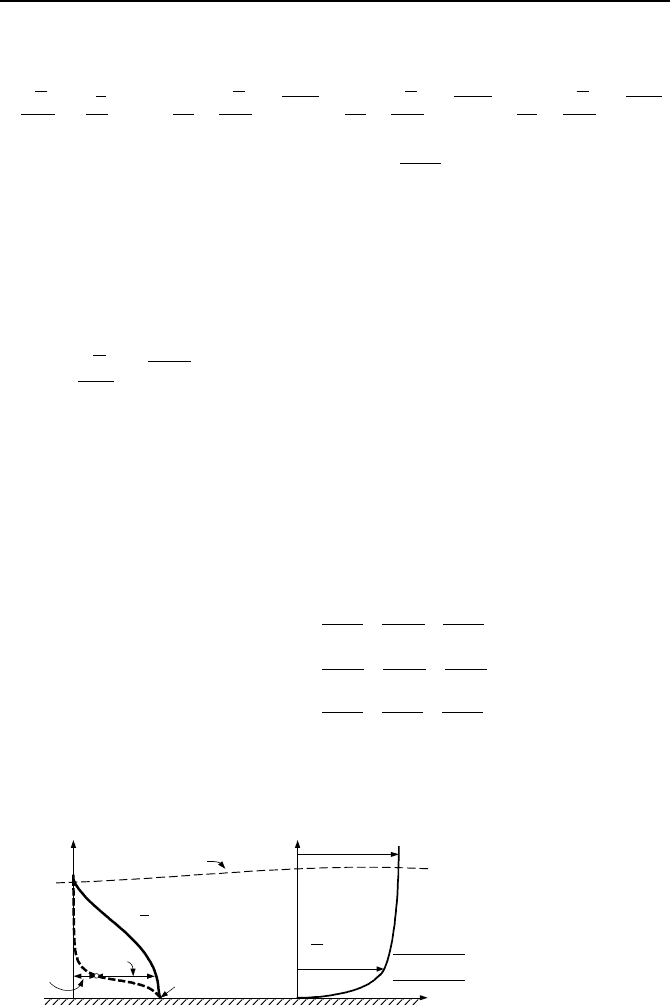
288 IIIb. Fluid Mechanics: Incompressible Viscous Flow

We may use the component of this equation along the x-axis. After substitution

and integration:

−

∂

−

∂

−

∂

−=

''''''

ρµρµρµρρ

Note that now some unfamiliar terms, such as

, appear. We could not get

rid of them the same way we got rid of the fluctuations by time averaging. These

terms are referred to as turbulent, eddy, or Reynolds shear stress even though they

are not shear stress. Rather, they appear as a result of fluid inertia manifested as

convective acceleration. These terms are called shear stress because they appear

next to the laminar shear stress term. As a result, shear stress in general is given

as:

TurbulentLaminar

ττρµτ

+=−

∂

A similar procedure can be applied to the two other components of the momentum

equation.

Let’s now consider a boundary layer developed when a fluid flows over a flat

plate. As shown in Figure IIIb.1.2, near the free stream, shear stress is all due to

turbulent shear. This contribution diminishes rapidly as we approach the wall,

dominated by viscous shear. Turbulent shear for incompressible fluid is a two-

dimensional tensor. The structure of this tensor in the Cartesian coordinate system

is given as:

−=

''''''

zzyzxz

zyyyxy

zxyxxx

zzzyzx

yzyyyx

xzxyxx

Turbulent

VVVVVV

τττ

V(x, y)

V(y)

Outer

Turbulent

Layer

Overlap Layer

Viscous Wall Layer

y = δ (x)

(x, y)

turb

lam

(x)

Figure IIIb.1.2. Profiles of shear stress and velocity in boundary layer

2. Steady Internal Incompressible Viscous Flow 289

Reynolds shear can be expressed in terms of velocity gradient, similar to the New-

ton law of viscosity. Boussinesq made this analogy by introducing the concept of

eddy viscosity to obtain:

−=

where

is known as eddy diffusivity for momentum. The quantity

ρε

is usually

interpreted as an eddy viscosity analogous to

, the molecular viscosity, but

whereas the

is a fluid property,

ρε

is a parameter of fluid motion. We study the

shear stresses in internal flow in the next section.

2. Steady Internal Incompressible Viscous Flow

The topic of internal flow covers the vast field of fluid flow in pipelines, fittings,

valves, pumps, and turbines.

Velocity Distribution

In Section 1 we noted that unlike laminar flow, in turbulent flow no simple rela-

tion exists between the shear stress and the mean velocity field. Hence, there is no

fundamental theory to determine the velocity distribution on a purely theoretical

basis. As a result, semi-empirical relations are used to determine the velocity field

in turbulent flow. In this section, both laminar and turbulent flows inside pipes are

studied and relevant correlations are presented.

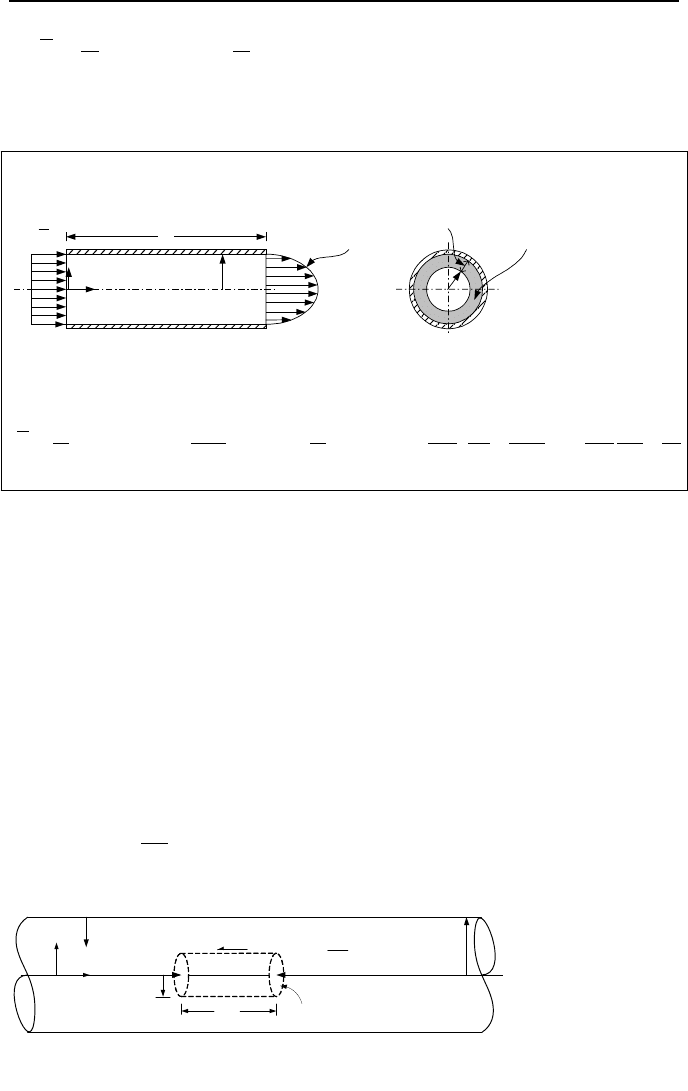
Shown in Figure IIIb.2.1 are the boundary layers for flow inside a pipe. For the

fully developed flow, flow can either be laminar or turbulent.

Parabolic

velocity

profile

max

Laminar flow

Turbulent flow

max

Figure IIIb.2.1. Shear stress and laminar and turbulent boundary layers in pipes

Our goal is to derive the profile for shear stress as well as the velocity profile

for both laminar and turbulent flow regimes. In these derivations, we will see that

the shear stress has a linear profile regardless of the flow regime. We will also see

that the laminar flow has a parabolic velocity profile where the maximum velocity

is much larger than the average velocity. In turbulent flow, the velocity profile is

much flatter than the laminar velocity profile. Thus, the maximum velocity is just

slightly larger than the average velocity. In the fully developed region, V

= 0 and

so is ∂V

/∂x = 0. In both flow regimes, the average velocity is obtained from:

290 IIIb. Fluid Mechanics: Incompressible Viscous Flow

()

rdx)

()

rdx

C.V.

Figure IIIb.2.2. Control volume for shear stress profile in laminar and turbulent flow in

pipes

³³

Area

dArV

dAxrV

V )(

),(

In this chapter, we use the average flow velocity at each cross section.

Example IIIb.2.1. The velocity distribution at the exit of a pipe is given. Find

the uniform inlet velocity in terms of the maximum velocity.

()

1),(

−= cLrV

= r/R

dA = 2

rdr

Solution: To find the uniform inlet velocity, we make use of the definition of av-

erage flow velocity:

)2()(1

),(

rdr

dAxrV

Area

−=

Shear Stress Distribution in Incompressible Viscous Flow in Pipes

Before deriving the shear stress profile, it is interesting to note that for an ideal

flow, pressure changes between two points if there is a change in flow area or ele-

vation. For viscous fluids, due to the existence of shear stresses, pressure changes

even though there is no change in flow area or elevation. To derive the shear

stress profile for steady incompressible viscous flow in pipes, a force balance for a

control volume as shown in Figure IIIb.2.2 is used. For fluid flowing in the x-

direction, pressure acting at the left area of the control volume is balanced by the

pressure acting on the right surface area and by the shear stress acting on the sur-

face area of the control volume. Note that we have used the first two terms of the

Taylor expansion for pressure. From a steady state force balance, we then find

that:

=−

+−

rdxrdx

PrP

τπππ

2. Steady Internal Incompressible Viscous Flow 291

which then simplifies to:

∂

−=

The maximum shear stress occurs at the surface or wall of the pipe (r = R).

Therefore, at the wall of the pipe:

∂

−=

We could obtain the same result by using the conservation equation for momen-

tum directly, as described in the next section.

Fully Developed Laminar Flow Inside Pipes

Once past the entrance region, the steady flow of an incompressible viscous flow

inside pipes would become fully developed. If the flow is laminar, the velocity

profile can be derived analytically by using the conservation equations of momen-

tum in a cylindrical coordinate system. As fluid flows along the x-axis, by using

symmetry, we note that velocity at any cross section changes only in the r-

direction (i.e., V

= V

(r)). Note that the same conclusion can be reached by using

the conservation equation of mass. The conservation equation of momentum in a

cylindrical coordinate system in the direction of flow (x-axis) gives:

()

∂

−−=

∂

τρ

where the only body force is gravity, which for horizontal flow has no component

in the x-direction. If flow is not horizontal, the term representing gravity should

be considered in the above equation. Integrating this equation, with boundary

condition of

at r = 0, yields the same results obtained in the previous sec-

tion for shear stress. To derive the velocity profile, the Newton law of viscosity

can be substituted in the profile for shear stress:

∂

−=

µτ

This equation can now be integrated with the boundary condition of V

= 0 at

r = R. Radially, r and y are in opposite direction. Thus, for the purpose of inte-

gration, we make a change of variable from dy to –dr to obtain:

−

∂

−=

)(

IIIb.2.1

indicating that velocity in laminar flow is a parabolic function in the r-direction.

This is known as Hagen-Poiseuille flow. The maximum velocity occurs at r = 0.

Hence, maximum velocity for laminar flow inside a pipe is given as: