Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


252 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
2
VVgBP V
t
ρρµ
∂
§·
+⋅∇ = +−∇+∇
¨¸
©¹
∂
KK
KK K K
K
IIIa.3.17
A one-dimensional form of the incompressible flow may be written as:
zzz
z
z
z
dF
z
P
Bg
z
V
V
t
V
−
∂
∂
−+=
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
ρρ
IIIa.3.18
where the fourth term on the right side of Equation IIIa.3.17 is written as a viscous
force in Equation IIIa.3.18. Velocity and viscous force terms always have differ-
ent signs. Determination of the viscous force is discussed in Section 4.
Ideal Flow (Euler Equation): For inviscid (frictionless,
µ
= 0), incompressi-
ble, and constant property flow, in the absence of body forces other than gravity,
the Navier-Stokes equation
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
simplifies to:
PgVV
t
∇−=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
K
K
K
K
K
ρρ
IIIa.3.19
This is the Euler equation. As discussed in Section 1, although all fluids possess vis-
cosity, some fluids behave as if they are inviscid. Hence, the Euler equation has
practical applications. Indeed, for high Reynolds numbers, the viscous effects for
most fluids are confined to a thin layer near the solid surface (i.e., the boundary
layer).
Very slow flow: in very slow or creeping flows, the Reynolds number is small,
indicating that the inertia effects can be neglected as the viscosity effects become
dominant. Hence, the convective acceleration term can be dropped. The Navier-
Stokes equation:
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
for very slow flow, in the absence of other body forces simplifies to:
VP
t
V
K
K
K
2
∇+∇−=
∂
∂
µρ
IIIa.3.20
Static fluid: in a static fluid, velocity is zero. Hence, the Navier-Stokes equa-
tion:
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
for static fluid, in the absence of other body forces except for gravity simplifies to

3. Conservation Equations 253
0=∇− Pg
K
K
ρ
IIIa.3.21
Integrating, the component in the
z-direction can be written in the familiar form of:
ZgP ∆=∆
ρ
IIIa.3.22
Next, we solve several problems regarding the application of the momentum equa-
tion.
Example IIIa.3.8. Write the momentum equation for an ideal flow in Cartesian
coordinates.
Solution: The momentum equation for an ideal fluid is the Euler’s equation as
given by Equation IIIa.3.19 in the general form. To obtain the components in Car-
tesian coordinates, we develop each term separately:
– Local acceleration:
)( k
t
V
j
t
V
i
t
V
t
V
z
y
x
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
ρρ
– Convective acceleration:
()
Vk
z
j
y
i
x
kVjViVVV
zyx
K
K
K
K
K
K
K
K
K
K
)]()[(
∂
∂
+
∂
∂
+
∂
∂
⋅++=∇⋅
ρρ
()
))([( kVjViV
z
V
y
V
x
VVV
zyxzyx
K
K
K
K
K
K
++
∂
∂
+
∂
∂
+
∂
∂
=∇⋅
ρρ
()
])(
)()[(
k
z
V
V
y
V
V
x
V
V
j
z
V
V
y
V
V
x
V
Vi
z
V
V
y
V
V
x
V
VVV
z
z
y
z
z
z
z
y
y
y
y
y
x
z
x
y
x
x
K
K
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=∇⋅
ρρ
– Gravity force:
)( kgjgigg
zyx
K
K
K
K
++=
ρρ
– Pressure force:
)( k
z
P
j
y
P
i
x
P
P
K
K
K
K
∂
∂
+
∂
∂
+
∂
∂
−=∇−
.
Therefore, the momentum equation for ideal flow in the Cartesian coordinate sys-
tem becomes:
x
P
g
z
V
V
y
V
V
x
V
V
t
V
x
x
z
x
y
x
x
x
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρρ
)(
y
P
g
z
V
V
y
V
V
x
V
V
t
V
y
y
z
y
y
y
x
y
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρρ
)(
z
P
g
z
V
V
y
V
V
x
V
V
t
V
z
z
z
z
y
z
x
z
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρρ
)(
254 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
Example IIIa.3.9. Find the governing equation for steady state incompressible
flow over a flat plate.
Solution: Starting with Equation IIIa.3.16, the first term in the left side and the
fourth term in the right side are canceled due to the steady and incompressible
fluid assumptions, respectively. If all body forces are also negligible then:
()
2
VV P V
ρµ
⋅∇ = −∇ + ∇
KK
KK K
If fluid flows in the x-direction over the surface then the x-component of the mo-
mentum equation is:
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
2
2
2
2
1
y
V
x
V
v
x
P
y
V
V
x
V
V
xxx
y
x
x
ρ
In the boundary layer over the plate, variation in V
x
in the x-direction is much less
than variation in V
x
in the y-direction and the first term in the parenthesis can be
neglected:
2
2
1
y
V
v
x
P
y
V
V
x
V
V
xx
y
x
x
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
ρ
IIIa.3.20-1
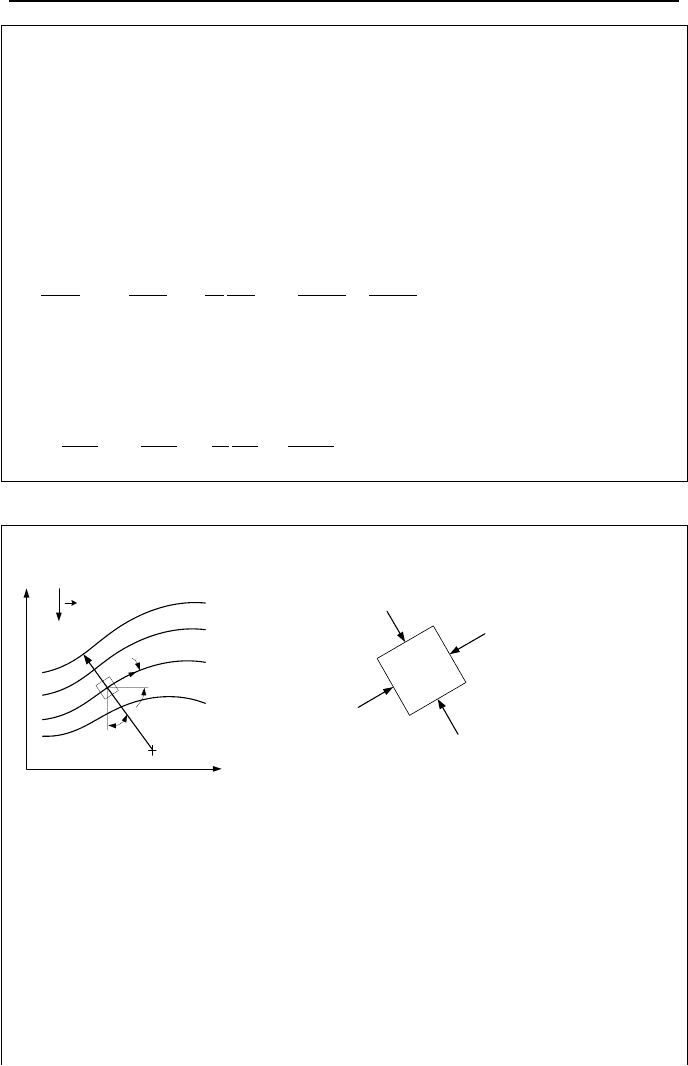
Example IIIa.3.10. Find the two-dimensional Euler’s equation along a streamline
(sn coordinate).
R
α
α
n
s
g
Pdsdx
ds
dn
y
z
[]
dsdxdnnPP )/( ∂∂+
Pdndx
[]
dndxdssPP )/( ∂∂+
Solution: The Euler’s equation along the streamlines can be derived directly by
applying Newton’s second law of motion to a differential control volume (dsdndx)
along the streamlines. For an ideal flow, only pressure and gravity forces need to
be considered. Along the streamline, the net pressure force becomes
dndxdssP ])/[( ∂∂− .
The component of the gravity force along the streamline becomes:
–
ρ
gcos(
α
) = –
ρ
g ∂ z/ ∂ s.
The summation of forces must be equal to mass times acceleration:
s
adsdndxdsdndxszgdndxdssP )()/(])/[(
ρρ
=∂∂−∂∂−
Canceling out dsdndx from both sides of the equation and substituting for the ac-
celeration in terms of the total derivatives yields:
3. Conservation Equations 255
0
1
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
s
z
g
s
P
s
V
V
t
V
ρ
A similar procedure yields Euler’s equation in the direction of the n-axis.
Example IIIa.3.11. Find the one-dimensional momentum equation for the flow of
a viscous fluid.
Solution: We consider the differential control volume where all dimensions are
lumped except for the dimension along the s-axis. In applying Equation IIIa.3.14
to this control volume, we note the pressure force, gravitational force, friction
force, and another body or surface force (dF
d
) other than friction and weight. Fi-
nally;
)()(cos
s
V
V
t
V
ds
dF
ds
dF
g
s
P
d
f
∂
∂
+
∂
∂
=+−+
∂
∂
ρθρ
where F
f
and F
d
are expressed as force per unit area.
ds
dA
P
V
dF
f
dF
d
P+(dP/ds)ds
θ
ρ
g(dAds)
Applicability of the Navier-Stokes Equations
These equations are applicable only to Newtonian fluids in laminar flow having
constant viscosity, (i.e., independent of spatial position). Adjustments must be
made to apply these equations to turbulent flow. It is interesting to note that the
non-linearity of these second order partial differential equations is not due to vis-
cous effects of the fluid, rather it is due to the inertial effects manifested in the
convective acceleration term. Except for the very slow flow, we were not able to
eliminate the source of non-linearity, even for the special flow cases discussed
above.
Conservation Equation of Energy, Differential Analysis
Compared with the momentum equation, derivation of the energy equation is sim-
pler since energy, like mass, is a scalar quantity. Hence, we find the rates of en-
ergy into and out of an elemental control volume from the three directions of x, y,
and z and simply add them up. Since similar processes exist in these three direc-
tions, we consider only the processes in the x-direction and apply the results to the
y- and z- directions. The rate of change of total energy of the elemental control
volume is due to the net exchange of energy into and out of the control volume.
This Eulerian approach for the energy equation is described next.

256 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
The flow of energy into and out of the control volume can be divided into two
groups. The first group includes the rate of energy exchange due to convection,
conduction, radiation, and internal heat generation. Convection is associated with
the flow of fluid carrying internal, kinetic, and potential energies, e
i
= u + K.E. +
P.E. Since the potential energy is very small, we only consider the internal and
the kinetic energies. To simplify the notations, we use the stagnation specific en-
ergy, defined as
1
u
o
= u + K.E. Total energy brought into the control volume from
face dydz is (
ρ
V
x
u
o
) dydz. Total energy leaving the control volume, is found by
Taylor expansion, using only the first two terms; (
ρ
V
x
u
o
) dydz + [∂(
ρ
V
x
u
o
)/
∂x]dxdydz . Hence, the net exchange of energy due to convection is found as –
[
∂(
ρ
V
x
u
o
)/∂x]dxdydz. Similarly, for the y- and z-directions, we find the net energy
exchange as –[
∂(
ρ
V
y
u
o
)/∂y]dxdydz and –[∂(
ρ
V
z
u
o
)/∂z]dxdydz, respectively.
()
()
()
()
Vu
z
uV
y
uV
x
uV
o
o
z
o
y
o
x
KK
ρ
ρ
ρ
ρ
⋅∇−=
»
»
¼
º
«
«
¬
ª
∂
∂
+
∂
∂
+
∂
∂
−
The internal heat generation is ( dxdydzq
′′′
), where q
′′′
is the volumetric heat gen-
eration rate. This term accounts for electric heating or fission heat generation in a
nuclear reaction. Conduction heat transfer needs to be expressed in terms of tem-
perature. As discussed in Chapter IVa, Fourier’s law relating heat flux to
temperature gradient (–k
∂
T/
∂
x) provides such a relation, where k is thermal
conductivity. Hence, the net exchange due to conduction heat transfer in the x-
direction is [
∂(k
∂
T/∂x)/∂x]dxdydz. Considering the y- and z-directions, the net
energy exchange due to conduction becomes:
()
Tk
z
zTk
y
yTk
x
xTk
∇∇=
∂
∂∂∂
+
∂
∂∂∂
+
∂
∂∂∂
K
K
.
)/()/()/(
For now, we represent the radiation heat transfer simply by
r
q
′′
. In Chapter IVd
we shall see that the Stefan-Boltzmann law relates
r
q
′′
to temperature. The net ex-
change due to radiation is, therefore, (
∂
r
q
′′
/∂x) + (∂
r
q
′′
/∂y) + (∂
r
q
′′
/∂z) per unit
volume. This can be expressed as
r
q
′′
⋅∇
K
K
per unit volume.
The second group of energy for the control volume includes the rate of work.
This in turn consists of three types of work. First, shaft work, which is clearly
zero for this elemental control volume. Second, work performed by the surface
forces. Third the work performed by the body forces. Work performed by the
surface forces consists of work performed by the normal and shear stresses. Since
work is defined as force multiplied by distance and the rate of work is defined as
force times velocity, work performed by the surface forces is non-zero only for the
velocity components, which are in the same direction as the surface force. For ex-
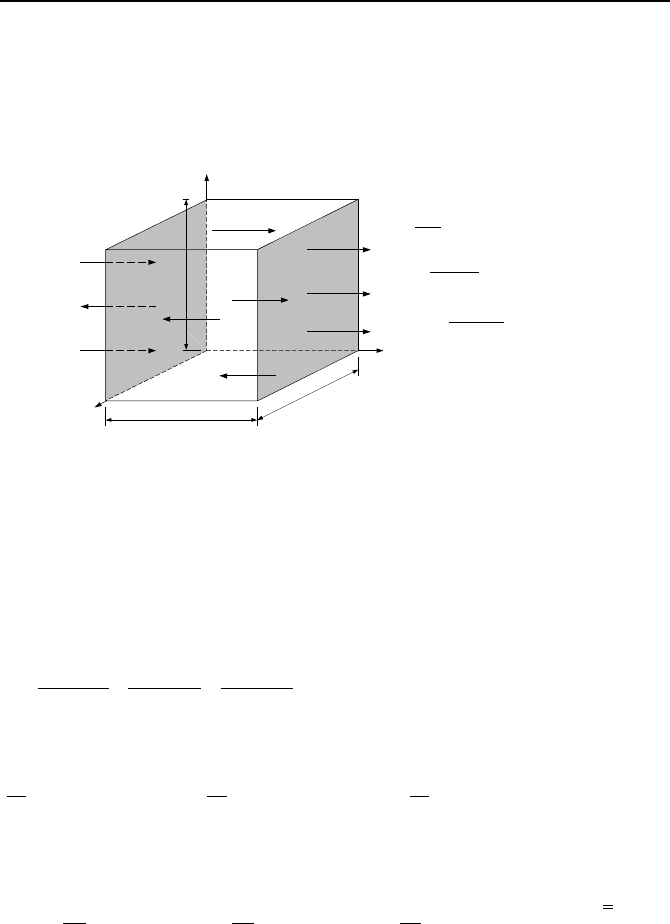
ample, as shown in Figure IIIa.3.3, the rate of work at x =0 due to normal stress in
the x-direction is given by –(
σ
x
dydz)V
x
and the rate of work due to shear stresses
1
The stagnation state is attained when a flowing fluid is brought to rest in an isentropic
process. Thus, h
o
= h + V
2
/2.
3. Conservation Equations 257
in the x-direction is given by –(
τ
xy
dxdy)V
y
and by –(
τ
xz
dxdz)V
x
(see also Fig-
ure IIIa.3.2). Hence, the total rate of work in the x-direction at x = 0 is found as:
()
(
)
()
VxdxdyVdxdyVdydz
zxxyxxx
ττσ
−−−
x
y
z
τ
yx
τ
zx
dx
dy
dydzq
x
′′
dydzdx
x
q
q
x
x
¸
¹
·
¨
©
§
∂
∂
+
dydzV
xx
σ
()
dydzdx
x
V
V
xx
xx
¸
¹
·
¨
©
§
∂
∂
+
σ
σ
dydzuV
o
x
)(
ρ
()
dydzdx
x
uV
uV
o
x
o
x
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
ρ
ρ
)(
dz
(
)
dyy
yxyx
∂∂+ /
ττ
dxdydzq
′′′
Figure IIIa.3.3. Influx and efflux of energy in the x-direction for an elemental control vol-
ume
The rate of work at x = dx is given by (
σ
x
dydz)V
x
+ ∂[(
σ
x
dydz)V
x
/∂x]dxdydz for
the normal stress and by (
τ
xy
dydz)V
y
+ [∂(
τ
xy
dydz)V
y
/∂x]dxdydz and (
τ
xz
dydz)V
z
+
[
∂(
τ
xz
dydz)V
z
/∂x] dxdydz, for the shear stress. Hence, the net rate of work ex-
change in the x-direction is:
()
(
)
()
»
¼
º
«
¬
ª
∂
∂
+
∂
∂
+
∂
∂
x
V
x
V
x
V
zxz
yxy
xx
τ
τ
σ
Thus the net rate of work exchange from all directions is found as:
()()()
()
VPVVV
z
VVV
y
VVV
x
yzyxzxzzzxzxyxyyzxzyxyxx
K
K
⋅∇=++
∂
∂
+++
∂
∂
+++
∂
∂
ττσττσττσ
+ Φ
where ĭ, referred to as viscous dissipation function, now stands for
()()()
yzyxzxzxzxyxzxzyxy
VV
z
VV
y
VV
x
ττττττ
+
∂
∂
++
∂
∂
++
∂
∂
=Φ
=
¸
¹
·
¨
©
§
⋅∇ V
K
K
τ
where the right-hand side term is the short hand representation of ĭ using tensor
notations for
τ
.
258 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
Example IIIa.3.12. Express the viscous dissipation function only in terms of ve-
locity components.
Solution: We can elegantly accomplish this task only for laminar flow. To do
this, we expand the terms comprising the net rate of work exchange and then sub-
stitute for the shear and normal stresses from the Newtonian fluid criteria and the
Stokes hypothesis, respectively. Expanding the net rate of work exchange:
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
x
V
z
V
z
V
y
V
y
V
x
V
z
V
y
V
x
V
V
yxz
V
xzy
V
zyx
z
x
zx
y
z
yz
x
y
xy
z
z
x
y
x
x
z
yz
xz
z
y
zx
zyy
x
zx
yx
x
τττσσσ
τ
τ
σ
τ
τσ
τ
τ
σ
We now substitute for the normal and shear stresses in terms of velocity from the
constitutive relations:
()
Φ+⋅∇−=
»
»
¼
º
«
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
−
»
»
¼
º
«
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
−
VP
x
V
z
V
z
V
y
V
y
V
x
V
x
V
x
V
x
V
x
V
x
V
x
V
x
V
x
V
x
V
P
z
x
y
z
x
y
xxxxxxxxx
KK
2
22
2222
3
2
2
µ
µ
µ
The first term represents the rate at which fluid is being compressed and the re-
maining terms comprise the viscous-dissipation function. The viscous-dissipation
function in Cartesian coordinates becomes:
»
»
¼
º
«
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
»
»
¼
º
«
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
=Φ
2
22
2
2
2
2
x
V
z
V
z
V
y
V
y
V
x
V
z
V
y
V
x
V
z
x
y
z
x
y
z
y
x
µµ
By using an order-of-magnitude analysis ĭ may be approximated as
ĭ =
µ
(įV
x
/įy)
2
.
Finally, the rate of work performed by body forces is simply found as BV
KK
⋅ .
The summation of all these rates of exchanges must be equal to the rate of change
of total energy of the elemental control volume (i.e.,
∂(
ρ
u
o
)dxdydz/∂t). Before we
write the final energy equation, we use the continuity equation as given by Equa-
tion IIIa.3.13, to simplify the rate of change of the control volume total energy,
∂(
ρ
u
o
)/∂t and the net energy exchange due to convection, as follows:
()
()
¸
¹
·
¨
©
§
⋅∇+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∇⋅+
∂
∂
=⋅∇+
∂
∂
V
t
uuV
t
u
Vu
t
u
oo
o
o
o
KKKKKK
ρ
ρ
ρρ
ρ
Thus we find:
BVVPqqTk
Dt
Du
uV
t
u
r
o
o
o
KKKK
K
KKKKK
⋅+Φ+⋅∇−
′′′
+
′′
⋅∇−∇⋅∇==
¸
¸
¹
·
¨
¨
©
§
∇⋅+
∂
∂
)()(
)(
ρρ
IIIa.3.23

3. Conservation Equations 259
Definition of terms from the left side is as follows:
t
u
o
∂
∂ )(
ρ
: local rate of change of the stagnation energy of the infinitesimal
control volume
o
uV ∇⋅
K
K
ρ
: rate of change in stagnation energy due to convection
)( Tk∇⋅∇
K
K
: net rate of heat transfer due to conduction
"
r
q
G
K
⋅∇ : net rate of heat transfer due to radiation
q
′′′
: rate of volumetric heat generation (electrical, chemical, or
nuclear reactions)
)( VP
K
K
⋅∇ : rate of work performed by pressure forces
Φ : rate of work performed by viscous forces
(viscous-dissipation function)
BV
KK
⋅ : rate of work performed by body forces, such as weight
The first and the second terms on the left side of Equation IIIa.3.23 are the Eule-
rian representation of the Lagrangian term for the net rate of change of the stagna-
tion energy. Next, we discuss the simplification of the energy equation for special
cases.
Inviscid fluid: For frictionless fluid flow, the rate of work performed by vis-
cous forces is zero. Hence,
BVVPqqTkuV
t
u
r
o
o
K
K
K
K
K
K
K
K
K
K
.)()(
)(
+⋅∇−
′′′
+
′′
⋅∇−∇⋅∇=∇⋅+
∂
∂
ρρ
Incompressible flow: For an incompressible flow, the rate of work performed
by pressure forces becomes zero. Hence;
BVqqTkuV
t
u
r
o
o
K
K
K
K
K
K
K
K
⋅+Φ+
′′′
+
′′
⋅∇−∇⋅∇=∇⋅+
∂
∂
)(
)(
ρρ
Ideal flow: For incompressible and inviscid flow, the energy equation further
simplifies to:
qqTkuV
t
u
r
o
o
′′′
+
′′
⋅∇−∇⋅∇=∇⋅+
∂
∂
K
K
K
K
K
K
)(
)(
ρρ
where in this equation the rate of work performed by body forces is also dropped
as compared with more dominant terms. If the net rate of heat transfer due to
thermal radiation can be ignored (as discussed in Chapter IVd, thermal radiation
becomes noticeable at elevated temperatures), we obtain
qTkuV
t
u
o
o
′′′
+∇⋅∇=∇⋅+
∂
∂
K
K
K
K
)(
)(
ρρ
260 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
Solid materials: Further simplification can be made in the energy equation if
applied to solids, in which case, the net rate of heat transfer due to convection
does not exist:
qTk
t
u
′′′
+∇⋅∇=
∂
∂
K
K
)(
)(
ρ
IIIa.3.24
Equation IIIa.3.24 is the basis of the conduction heat transfer, which is discussed
in Chapter IVa.
Example IIIa.3.13. Find the governing equation for steady state incompressible
flow over a flat plate.
Solution: Starting with Equation IIIa.3.23, the first term in the left-hand side and
the fourth term in the right-hand side are canceled due to the steady and incom-
pressible fluid assumptions, respectively. The equation then reduces to:
BVqqTkuV
r
o
K
K
K
K
K
K
K
K
⋅+Φ+
′′′
+
′′
⋅∇−∇⋅∇=∇⋅ )(
ρ
If the effect of all body forces is also negligible, there is no internal heat genera-
tion, and we ignore contribution by thermal radiation then we get:
Φ+∇⋅∇=∇⋅ )( TkuV
K
K
K
K
ρ
Substituting for u in terms of temperature, developing terms, substituting for vis-
cous-dissipation function, and considering only two-dimensional flow, the equa-
tion becomes:
2
2
2
2
2
2
2
22
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
y
V
x
V
c
v
y
V
c
v
x
V
c
v
y
T
x
T
y
T
V
x
T
V
xx
y
x
yx
α
In the boundary layer, variation in V
x
in the x-direction is much less than variation
in V
x
in the y-direction and the first term in the second parenthesis can be ne-
glected. Also neglecting ∂V
y
/∂y and temperature variations in the x-direction, the
above equation simplifies to:
2
2
2
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
y
V
c
v
y
T
y
T
V
x
T
V
x
yx
α
Ignoring viscous dissipation, the above equation further simplifies to:
2
2
y
T
y
T
V
x
T
V
yx
∂
∂
=
∂
∂
+
∂
∂
α
IIIa.3.23-1
Note the striking resemblance between Equations IIIa.3.20-1 (in the absence of the
pressure gradient term) and IIIa.3.23-1.
As we shall see in Chapter IIIb, the viscous dissipation function results in a
pressure drop, which is traditionally expressed as head loss. Due to analytical

3. Conservation Equations 261
complexities associated with flow fluctuations, pressure drop in turbulent flow due
to viscous effects are generally obtained in experiments.
3.3. Derivation of the Bernoulli Equation
The Bernoulli equation is a simplified form of the one-dimensional momentum
equation. The goal here is to show that under certain circumstance, the Bernoulli
equation can also be derived from the conservation equation of energy. The Ber-
noulli equation written as:
constant
2
2
=++ gZ
V
P
ρ
ρ
states that the total mechanical energy of an incompressible, inviscid flow along a
streamline always remains a constant as shown in Figure IIIa.3.4(a). This is dis-
cussed in more detail in the next two sections.
Derivation of Bernoulli Equation from Energy Equation
Although the Bernoulli equation and the equation for conservation of energy are,
in general, independent equations, the purpose here is to show that in certain cir-
cumstances, the Bernoulli equation can be derived from the equation for conserva-
tion of energy. These include the assumptions of steady flow, no heat, and no
work transfer. To demonstrate, consider Equation IIIa.3.11 for steady and uni-
form flow at the inlet and outlet ports of a fixed control volume:
µ
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
+++++=
¦¦
exit
inlet
vs
gdZ
dVdP
dumWWQ
2
2
ρ
IIIa.3.25
where in Equation IIIa.3.25 we have retained the work done by the viscous forces.
Dividing Equation IIIa.3.25 by mass flow rate, and integrating the specific internal
energy, yields:
2
()
2
exit
sv ei
inlet
dP dV
qw w u u gdZ
ρ
´
µ
µ
µ
¶
§·
=++ −+ + +
¨¸
©¹
IIIa.3.26
This equation can be slightly rearranged to get:
[]
0
2
)(
2
=
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
+++−−++
exit
inlet
ievs
gdZ
dVdP
quuww
ρ
IIIa.3.27
Let’s now evaluate the left side term. This term consists of shaft work, viscous
work, heat transfer, and dissipation. In the absence of any of these effects, Equa-
tion IIIa.3.27 becomes the Bernoulli equation provided that the flow is incom-
pressible. Therefore, we were able to derive the Bernoulli equation from the con-
servation equation for energy for an incompressible flow and for the condition that
