Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

242 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
³³³³³
¦¦
⋅+
¸
¹
·
¨
©
§
∂
∂
=+
....
)(V
SCVC
ForceSurfaceForceBody
SdVVdV
t
FF
K
KKKKK
ρρ
IIIa.3.6
where in Equation IIIa.3.6, the first term in the right side is the rate of change of
momentum within the control volume and the second term is the net momentum
flux through the control volume. Equation IIIa.3.6 is a vector equation having
components in three dimensions. Application of the one-dimensional momentum
equation is explored in various Chapters of this book.
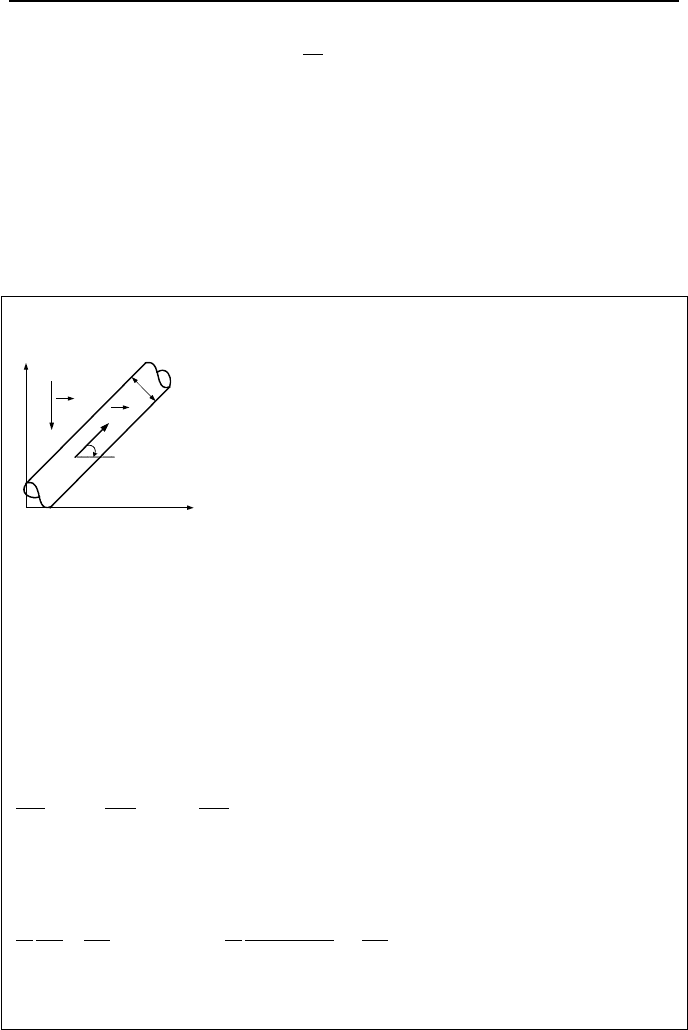
Example IIIa.3.1. Write the integral momentum equation for a one-dimensional
(1-D) flow.
x
y
F
l
o
w
β
V
s + ds
d
s
s
g
D
Solution: We use the control volume in the figure (dV = Ads) and follow Equa-
tion IIIa.3.6. The first term in the right side of this equation is the rate of change
of momentum in the control volume which becomes (d m
/dt)ds. The second term
in the right side is the momentum flux [(
2
m
/
ρ
A)
s+ds
– (
2
m
/
ρ
A)
s
]. The body
force is the fluid weight and the surface forces are the friction force (F
F
) and the
pressure force.
¦
−−−=
+ Fdsss
dFgAdsPPAdF
βρ
sin)()(
where
β
is measured from the horizontal plane. Substituting:
()
22
(sin )
s
sds F
sds s
dm m m
ds A P P A gds dF
dt A A
ρβ
ρρ
+
+
ªº
§· §·
+−=−− −
«»
¨¸ ¨¸
©¹ ©¹
¬¼
We rearrange this equation by dividing both sides by Ads and letting ds approach
zero:
F
s
P
s
Am
A
g
s
P
t
m
A
¸
¹
·
¨
©
§
∂
∂
−
∂
∂
−−
∂
∂
=
∂
∂
)/(1
)(sin
1
2
ρ
βρ
IIIa.3.6-1
where the differential friction force is now written in terms of the friction pressure
drop.

3. Conservation Equations 243
Conservation Equation of Energy, Integral Approach
In the case of conservation equation of energy, Y = E and y = dE/dm = e where E
and e are total and specific energy of the system, respectively. Substituting these
in Equation IIIa.3.1 yields:
()
³³³³³
⋅+
¸
¹
·
¨
©
§
∂
∂
=
....
)(V
SCVC
System
SdVede
t
E
Dt
D
K
K
ρρ
IIIa.3.7
The left side in the above equation is the Lagrangian expression of the rate of
change of total system energy. This according to the first law of thermodynamics
is related to the rate of work and heat transfer to or from the system as follows:
¦¦
−= WQE
Dt
D
System
)( IIIa.3.8
Substituting yields:
³³³³³
¦¦
⋅+
¸
¹
·
¨
©
§
∂
∂
=−
....
)(V
SCVC
SdVede
t
WQ
K
K
ρρ
IIIa.3.9
As was discussed in Chapter II, The rate of work transfer to or from the control
volume may consist of several types including the shaft work, the pressure work,
the viscous work (due to the surface shear stresses), and work due to electric and
magnetic fields, etc. Therefore, the rate of work transfer becomes:
()
³³
³³
"
K
K
K
K
+++−+=
¦
MagneticElectric
SCSC
s
WWSdSdVPWW
....
..
τ
IIIa.3.10
We may partition the pressure work by taking the surface integral on all the ports
(both inlet and exit) and the remaining of the control surface:
.. .., .., ..,
(.) (.) (.) (.) V
CS CS ports CS remaining CS ports
P
VdS PVdS PVdS PVdS P=+ =+
³³ ³³ ³³ ³³
KK KK
KK KK
By partitioning the integral, we explicitly consider the work due to changes in the
boundary of a deformable control volume. If the control surface is not deform-
able, then the last term on the right side is zero. As for the viscous work, except in
the case of very slow or so called creep flow, where viscosity effects are domi-
nant, the rate of work transfer due to viscous forces is negligible compared to the
shaft work. Substituting for the total rate of work transfer in the integral energy
equation and using the constituents of the total specific energy (i.e., specific inter-
nal u, kinetic
ρ
V
2
/2, and potential
ρ
gZ energies):
gZVue
ρρ
++= 2/
2
the first law of thermodynamics can be written as:
()
µ
¶
´
µ
¶
´
⋅
¸
¸
¹
·
¨
¨
©
§
++++
µ
¶
´
µ
¶
´
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
++
∂
∂
++
¦
=
¦
portsSCC.V.
s
SdVgZ
VP
udgZ
V
u
t
PWQ
.,.
22
2
V
2
V
K
K
ρ
ρ
ρ
IIIa.3.11

244 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
In Equation IIIa.3.11, we have considered only shaft work and pressure work due
to changes in the control surface. Also note that the triple integral over the control
volume represents total energy of the C.V.:
µ
µ
¶
´
µ
µ
¶
´
µ
µ
¶
´
¸
¸
¹
·
¨
¨
©
§
++=
..
2
.
V
2
VC
VC
dgZ
V
uE
ρ
Using the definition of enthalpy (h = u + Pv), Equation IIIa.3.11 can be written in
terms of flow enthalpy entering and leaving the control volume:
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
+++
¸
¸
¹
·
¨
¨
©
§
++++=
′′′
++
¸
¸
¹
·
¨
¨
©
§
++
¦¦¦¦
gZ
V
um
dt
d
gZ
V
hmPWqQgZ
V
hm
e
e
e
ee
i
si
i
ii
22
VV
2
2
22
IIIa.3.12
where in Equation IIIa.3.12,
q
′′′
is the volumetric heat generation rate (kJ/m
3
or
Btu/ft
3
, for example) in the control volume due to such effects as electric resis-
tance, exothermic chemical reactions, nuclear heat generation, etc. The volumet-
ric heat generation rate from nuclear reactions is discussed in Chapter VIe.
It is important to recall our sign convention as discussed in Chapter II, for
Q
and ,W
the rate of heat transfer and power, respectively. The rate of heat transfer
has a plus sign if heat is added to the system and has a minus sign if heat is re-
moved from the system. Power, has a plus sign if work is performed by the sys-
tem and has a minus sign if work is delivered to the system. Therefore, power de-
livered by a turbine is positive and power delivered to a pump or a compressor is
negative. Similarly, the heat transfer delivered to a boiler or to the core of a nu-
clear reactor is positive and the heat loss from a pump or a turbine is negative.
Equation IIIa.3.12 represents the integral form of the energy equation for a de-
formable control volume. For steady state processes and control volumes with
fixed boundaries and no internal heat generation, Equation IIIa.3.12 simplifies to:
¦¦¦¦
¸
¸
¹
·
¨
¨
©
§
+++=+
¸
¸
¹
·
¨
¨
©
§
++
e
e
e
ee
i
si
i
ii
gZ
V
hmWQgZ
V
hm
22
22
IIIa.3.12-1
For steady state and steady flow processes Equation IIIa.3.12-1 is further simpli-
fied to:
¸
¸
¹
·
¨
¨
©
§
+++=+
¸
¸
¹
·
¨
¨
©
§
++
¦¦
e
e
esi
i
i
gZ
V
hwqgZ
V
h
22
22
IIIa.3.12-2
where
q and w
s
are heat and shaft work transfer per unit mass of the working
fluid, respectively. Although the equations for conservation of momentum and
conservation of energy are independent, as is shown later in this section, under
certain circumstance they would lead to a similar conclusion. The case in point is
the well-known Bernoulli equation.

3. Conservation Equations 245
3.2. Differential Analysis of Conservation Equations
There are generally three methods to derive the conservation equations in their dif-
ferential forms. In the first method, the differential forms for the conservation
equations are derived from the integral form by using the vector calculus, specifi-
cally the Gauss divergence theorem (Chapter VIIc). In the second method, the in-
tegral approach is applied to a control volume and the differential formulation is
derived by taking the limit as the volume becomes infinitesimal. In the third
method, the conservation equations are directly derived for an infinitesimal con-
trol volume using the Eulerian approach.
Conservation Equation of Mass, Differential Analysis
To derive the differential form of the continuity equation, we consider flow of
fluid through an elemental control volume, dxdydz, as shown in Figure IIIa.3.1.
For simplicity, we have only shown flow though the yz-plane in the x-direction.
The rate of mass entering the control volume at x = 0 is (
ρ
V
x
)dA = (
ρ
V
x
)(dydz).
Similarly, we can find the mass flow rate entering the control volume through the
xy- and xz-planes. Since mass is a scalar quantity, we can add all these mass flow
rates to find the total rate of mass entering the control volume from all directions
as:
(
ρ
V
x
)dydz + (
ρ
V
y
)dxdz + (
ρ
V
z
)dxdy
We now find the mass flow rate leaving the control volume in the x-direction
through the yz-plane located at x = dx. This is found from the Taylor expansion of
the function (
ρ
V
x
)dydz, by using only the first two terms. This amounts to [
ρ
V
x
+
∂(
ρ
V
x
)/∂x](dydz). Similarly, we find the mass flow rate into the control volume in
the y- and z-directions. Hence, total mass of fluid flowing out of the control vol-
ume becomes:
¿
¾
½
¯
®
»
¼
º
«
¬
ª
∂
∂
++
°
¿
°
¾
½
°
¯
°
®
»
¼
º
«
¬
ª
∂
∂
++
¿
¾
½
¯
®
»
¼
º
«
¬
ª
∂
∂
+ dxdydz
z
V
dxdyVdxdzdy
y
V
dxdzVdydzdx
x
V
dydzV
z
z
y
y
x
x
)(
)(
)(
)(
)(
)(
ρ
ρ
ρ
ρ
ρ
ρ
x
y
z
(
ρ
V
x
)dydz
dx
dz
dy
Control Volume
(
ρ
V
x
)dydz +
dydzdx
x
V
x
»
¼
º
«
¬
ª
∂
∂ )(
ρ
Figure IIIa.3.1. Flow of fluid through an elemental control volume in Cartesian coordi-
nates

246 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
The rate of change of mass of the control volume is due to the difference in the in-
coming and outgoing flows:
=
∂
∂
)( dxdydz
t
ρ
dxdydz
z
V
dxdzdy
y
V
dydzdx
x
V
z
y
x
»
¼
º
«
¬
ª
∂
∂
+
»
¼
º
«
¬
ª
∂
∂
+
»
¼
º
«
¬
ª
∂
∂
−
)(
)(
)(
ρ
ρ
ρ
This equation simplifies to:
0
)(
)(
)(
=
»
¼
º
«
¬
ª
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
V
y
V
x
V
t
z
y
x
ρ
ρ
ρ
ρ
The general form of the continuity equation that is independent of any coordinate
system can be written as:
0=⋅∇+
∂
∂
V
t
K
K
ρ
ρ
IIIa.3.13
where in Equation IIIa.3.13, density is a function of space and time
),,,( tzyxf=
ρ
. Equation IIIa.3.13 is valid for any flow field condition whether
it is steady or unsteady, viscous or frictionless, compressible or incompressible.
However, this equation is not valid when there is any source or sink singularities
in the control volume such as occurrence of condensation or boiling. Also, nu-
clear reactions in which conversion of mass and energy may exist are excluded.
Under a steady state condition, the second term is identically zero as, despite
the possible existence of a spatial distribution for density, such a distribution
would not change with time. The continuity equation is in its simplest form if a
fluid is incompressible, since density at constant temperature in an incompressible
flow field is constant. Gases can be treated as incompressible fluid as long as the
gas velocity remains less than about 30% of the speed of sound in the gas (
≈ 300
ft/s or 91.5 m/s). Next we solve several examples using various forms of the con-
tinuity equation.
Example IIIa.3.2. Use Equation IIIa.3.13 and derive the continuity equation in
terms of the substantial derivative of density.
Solution: We first carryout the differentiation in Equation IIIa.3.13:
0=∇⋅+⋅∇+
∂
∂
=⋅∇+
∂
∂
ρρ
ρ
ρ
ρ
K
K
K
K
K
K
VV
t
V
t
in Cartesian coordinates:
0)()( =
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
V
y
V
x
V
z
V
y
V
x
V
t
zyx
z
y
x
ρρρ
ρ
ρ
We now collect the first term and the terms in the second parenthesis and use
Equation IIIa.2.2:
0=⋅∇+ V
Dt
D
K
K
ρ
ρ
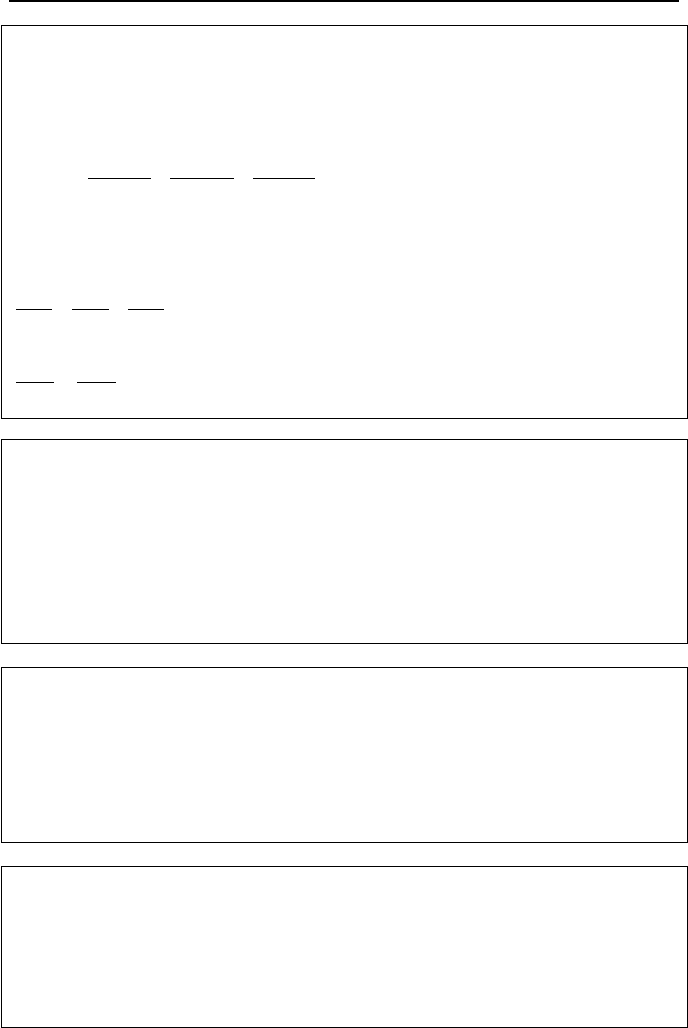
3. Conservation Equations 247
Example IIIa.3.3. Write the continuity equation in Cartesian coordinates for a)
steady flow and b) incompressible flow.
Solution: a) For steady flow, we use Equation IIIa.3.13 and drop the first term.
We also note that for steady flow ),,( zyxf=
ρ
:
0
)(
)(
)(
=
∂
∂
+
∂
∂
+
∂
∂
=⋅∇
z
V
y
V
x
V
V
z
y
x
ρ
ρ
ρ
ρ
K
K
b) For incompressible flow =
ρ
constant (i.e., ∂
ρ
/
∂
t = 0). Hence, Equation
IIIa.3.13 becomes 0=⋅∇ V
K
K
ρ
or alternatively 0=⋅∇=⋅∇ VV
K
G
K
K
ρρ
. That is to say
0=
∂
∂
+
∂
∂
+
∂
∂
z
V
y
V
x
V
z
y
x
. In two dimensions, we have:
0=
∂
∂
+
∂
∂
y
V
x
V
y
x
IIIa.3.13-1
Example IIIa.3.4. Consider a planar flow with the component of velocity along
the x-axis given as V
x
=xy and the component of velocity along the y-axis given
as V
y
= –2y. Do these components represent an incompressible flow?
Solution: To have a planar incompressible flow, we must be able to show that
∂V
x
/∂x + ∂V
y
/∂y = 0 is met. Taking the derivative and substituting, we get y – 2 ≠
0 which does not satisfy the continuity equation. Therefore, the above compo-
nents do not represent an incompressible flow. The reader may verify that the fol-
lowing components do represent an incompressible flow; V
x
= 2xy and V
y
= –y
2
.
Example IIIa.3.5. Does vector kbxzayzjayzibzaxyt
K
K
K
K
)()(
2
++−+=
υ
represent
the velocity vector of an incompressible flow field?
Solution: For incompressible flow, we must have ∂
υ
x
/∂x + ∂
υ
y
/∂y + ∂
υ
z
/∂z = 0.
Finding components:
∂
υ
x
/∂x = ayt, ∂
υ
y
/∂y = –az
2
, and ∂
υ
z
/∂z = ay + bx. The summation is not zero thus
υ
is not a velocity vector in an incompressible flow.
Example IIIa.3.6. Consider a planar incompressible flow with the component of
velocity along the x-axis given as V
x
= c
1
x
2
y +c
2
x. Find V
y
.
Solution: Since for a two-dimensional flow, the continuity equation simplifies to
0// =∂∂+∂∂ yVxV
yx
. Having V
x
, we find dV
x
/dx = 2c
1
xy + c
2
. Hence,
)2(/),(
21
cxycyyxV
y
+−=∂∂ . Integrating, V
y
= – (c
1
xy + c
2
)y + c
3,
where c
3
is
the constant of integration and is found from the boundary condition.

248 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
Example IIIa.3.7. Start with integral analysis and obtain the differential equation
of the conservation of mass for the control volume of Example IIIa.3.1 for
β
= 0.
Solution: For a horizontal control volume, we replace s with x. According to
Equation IIIa.3.2, the rate of change of mass in the control volume is equal to the
mass flux through the control volume, hence
() ()
»
¼
º
«
¬
ª
∂
∂
+−=
∂
∂
dx
x
VA
VAVA
t
ρ
ρρ
ρ
V
This equation simplifies to
()
0//)( =∂∂+∂∂ xVt
ρρ
. Carrying out the differentia-
tion and rearranging
0
111
=
∂
∂
+
∂
∂
+
∂
∂
xx
V
VtV
ρ
ρ
ρ
ρ
Conservation Equation of Momentum, Differential Analysis
Shown in Figure IIIa.3.2 is an elemental control volume of a fluid being traced in
a flow field. The applied forces on this control volume, due to the acting stresses,
consist of body and surface forces:
¦¦ ¦
+=
ForceSurfaceForceBody
FdFdFd )()(
K
K
G
The body forces include weight and forces induced by an electromagnetic field,
for example:
¦
+= BgFd
ForceBody
K
K
K
ρ
)(
The surface forces are due to pressure and shear stresses. To find the expression
for these forces, let’s look only at the surface forces in the x-direction:
z
x
y
τ
zx
τ
yx
σ
x
dx
x
x
x
∂
∂
+
σ
σ
dz
z
zx
zx
∂
∂
+
τ
τ
dy
y
yx
yx
∂
∂
+
τ
τ
dx
dz
dy
Control
Volume
Figure IIIa.3.2. Components of normal and shear stresses in the x-direction for an infini-
tesimal fluid element
The net surface force in the x-direction due to the normal and tangential (shear)
stresses becomes:
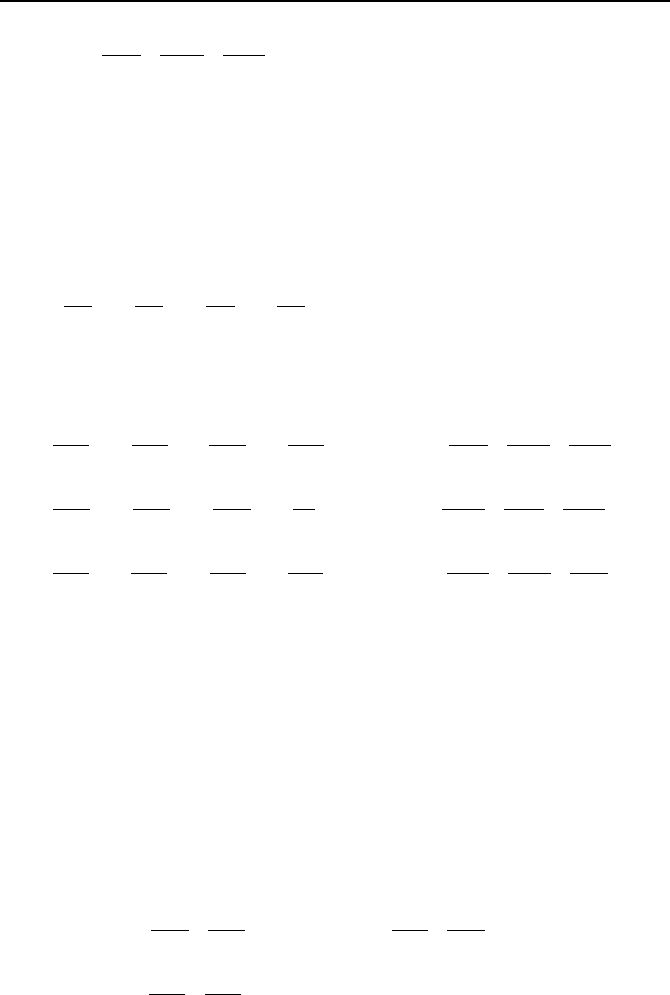
3. Conservation Equations 249
dxdydz
zyx
dF
zx
yx
x
xs
)(
,
∂
∂
+
∂
∂
+
∂
∂
=
τ
τ
σ
Similarly, the body forces with components in the x-direction become:
dxdydzBgdF
xxxB
)(
,
+=
ρ
We can write similar expressions for differential force components in the y- and z-
directions as act on the differential element dxdydz. According to Newton’s sec-
ond law of motion, the applied forces result in the fluid particle acceleration.
Thus, in this Lagrangian approach we can then write:
Fd
z
V
V
y
V
V
x
V
V
t
V
dm
zyx
K
K
K
K
K
=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
Substituting for dm =
ρ
dxdydz, where
ρ
is expressed in kg/m
3
in SI units or
slug/ft
3
in BU, yields:
zyx
Bg
z
V
V
y
V
V
x
V
V
t
V
zx
yx
x
xx
x
z
x
v
x
x
x
∂
∂
+
∂
∂
+
∂
∂
++=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
τ
τ
σ
ρρ
zyx
Bg
z
v
V
y
V
V
x
V
V
t
V
zyyxy
yyz
y
y
y
x
y
∂
∂
+
∂
∂
+
∂
∂
++=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
τστ
ρρ
zyx
Bg
z
V
V
y
V
V
x
V
V
t
V
z
yz
xz
zz
z
z
z
y
z
x
z
∂
∂
+
∂
∂
+
∂
∂
++=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
σ
τ
τ
ρρ
These are the three components of the momentum equation (known as the Cauchy
momentum equation), written in terms of normal and shear stresses. These equa-
tions are applicable to both Newtonian and non-Newtonian fluids as long as the
continuum hypothesis is satisfied. It is the substitution for the normal and shear
stresses that makes the equations peculiar to either Newtonian or non-Newtonian
fluids.
Momentum Equation for Newtonian Fluids (The Navier-Stokes Equations)
In Section 1 we discussed that one of the criteria for a Newtonian fluid is to be
able to relate the shear stress to velocity in the form of:
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
==
y
V
x
V
x
y
yxxy
µττ
,
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
==
z
V
y
V
y
z
zyyz
µττ
, and
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
==
x
V
z
V
z
x
xzzx
µττ
According to the Stokes hypothesis, we can show (Aris, Daily, and Schlichting)
that for Newtonian fluids:
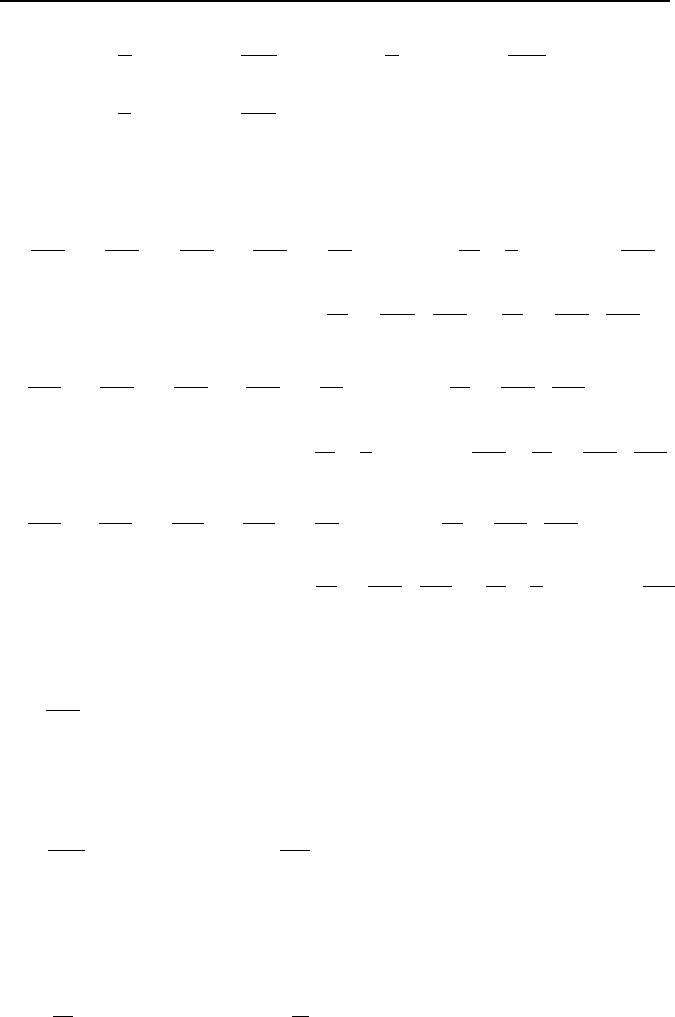
250 IIIa. Fluid Mechanics: Single-Phase Flow Fundamentals
()
x
V
VP
x
x
∂
∂
+⋅∇−−=
µµσ
2
3
2
K
K
,
()
y
V
VP
y
y
∂
∂
+⋅∇−−=
µµσ
2
3
2
K
K
, and
()
z
V
VP
z
z
∂
∂
+⋅∇−−=
µµσ
2
3
2
K
K
Substituting the above expressions, for stress in terms of velocity, in the momen-
tum equation we obtain:
()
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
∂
∂
+
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
∂
∂
+
¸
¹
·
¨
©
§
∂
∂
+⋅∇−
∂
∂
+++
∂
∂
−=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
x
V
z
V
zy
V
x
V
y
x
V
V
x
Bg
x
P
z
V
V
y
V
V
x
V
V
t
V
z
xx
y
x
xx
x
z
x
y
x
x
x
µµ
µµρρ
2
3
2
KK
()
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
∂
∂
+
¸
¸
¹
·
¨
¨
©
§
∂
∂
+⋅∇−
∂
∂
+
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
∂
∂
+++
∂
∂
−=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
y
V
z
V
zy
V
V
y
y
V
x
V
x
Bg
y
P
z
V
V
y
V
V
x
V
V
t
V
z
yy
x
y
yy
y
z
y
y
y
x
y
µµµ
µρρ
2
3
2
KK
()
¸
¹
·
¨
©
§
∂
∂
+⋅∇−
∂
∂
+
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
∂
∂
+
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
∂
∂
+
∂
∂
∂
∂
+++
∂
∂
−=
¸
¸
¹
·
¨
¨
©
§
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
V
V
zy
V
z
V
y
z
V
x
V
x
Bg
z
P
z
V
V
y
V
V
x
V
V
t
V
zz
y
x
z
zz
z
z
z
y
z
x
z
µµµ
µρρ
2
3
2
KK
These equations can be generalized in the vector form of:
¦
= Fd
Dt
VD
K
K
ρ
IIIa.3.14
Substitution of forces in Equation IIIa.3.14 yields the momentum equation in the
Cartesian coordinates:
[]
)(
3
4
VVBgP
Dt
VD
K
K
K
K
K
K
K
K
K
×∇×∇+
»
¼
º
«
¬
ª
⋅∇∇+++∇−=
µ
µ
ρρ
IIIa.3.15
This equation allows for variation of fluid viscosity as a function of position. In
many applications viscosity is independent of location. In this case, Equa-
tion IIIa.3.15 simplifies to:
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
IIIa.3.16
3. Conservation Equations 251
where the left side of Equation IIIa.3.16 is expanded according to Equa-
tion IIIa.2.3. The assumption of constant viscosity (i.e., independent of spatial po-
sition) allowed us to take the viscosity term outside the differentiation. This sim-
pli
fied set of vector equations (IIIa.3.16) is known as the Navier-Stokes
equa
tions as Louis Marie Henri Navier (1785 – 1836) first derived these equa-
tions for incompressible fluids in 1822. George Gabriel Stokes (1819–1903) gen-
eralized the derivation in 1845
+
.
Definition of terms in the Navier-Stokes equations is as follows.
()
tV ∂∂ / : local acceleration
(
)
VV
K
K
K
∇⋅ convective acceleration
g
K
ρ
: gravity force
B
K
: remaining body force (electrical force in a magnetic field)
P∇
K
: pressure force
()
VV
K
K
K
K
2
3
∇+⋅∇∇
µ
µ
: viscous shear forces
To this date no analytical solution in closed form exists for the Navier-Stokes
equation. We therefore investigate special cases by neglecting certain terms in
these equations as the flow condition permits.
The Navier-Stokes equations in the cylindrical and spherical coordinate sys-
tems are given in Tables A.III.4 and A.III.5, respectively.
Steady flow: In steady flow, local acceleration from the Eulerian point of view
is zero (
0/ =∂∂ tV
K
). Hence, the Navier-Stokes equation:
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
for steady flow simplifies to:
() ()
2
3
VV gBP V V
µ
ρρ µ
⋅∇ = + −∇ + ∇ ∇⋅ + ∇
KKKK
KK K K K
K
Incompressible flow: Variation in fluid density in incompressible flow is neg-
ligible. Hence, as shown in Example IIIa.3.2,
0=⋅∇ V
KK
so that the Navier -
Stokes equation:
()
VVPBgVV
t
K
K
K
K
K
K
K
K
K
K
2
3
∇+⋅∇∇+∇−+=
¸
¹
·
¨
©
§
∇⋅+
∂
∂
µ
µ
ρρ
for incompressible flow simplifies to:
+
According to Eckert, “these equations were first derived by N. Navier and S. P. Poisson
from a consideration of intermolecular forces and by B. de Saint Venant and Stokes based
on the assumption that the normal and shear stresses in a fluid are proportional to the de-
formation velocities.”
